基于单频正交线偏振光的激光波长直接测量方法

严利平，刘朋朋，谢建东，陈本永

(浙江理工大学纳米测量技术实验室，杭州 310018)

基于单频正交线偏振光的激光波长直接测量方法

严利平，刘朋朋，谢建东，陈本永

(浙江理工大学纳米测量技术实验室，杭州 310018)

提出了一种激光波长的直接测量方法，将对未知波长的测量转化为干涉条纹信号整周期计数和两路干涉信号相位差的测量，不需要参考光源，能实现激光波长的大范围高精度连续直接测量。介绍了系统的光路结构和激光波长直接测量原理，设计了基于FPGA的整数干涉条纹计数和小数干涉条纹相位差测量的干涉信号处理方法。对He-Ne激光器测量实验结果表明：激光波长测量误差小于0.27 pm，测量不确定度为4.5×10-7，由此验证了该方法的可行性以及干涉信号处理方法的有效性。

光波长测量；干涉仪；相位差测量；FPGA

0 引 言

长度基准是保证量值准确和实现互换性的基础，现行长度基准“米”采用激光波长作为复现手段。激光波长作几何测量的标尺，被广泛应用于激光干涉仪中用于测量位移、角度、粗糙度和直线度等几何量，是超精密加工、微电子制造以及精密计量领域中的重要参数。因此精确地测量波长大小是保证几何量测量准确性和量值溯源的关键[1-4]。激光波长测量方法大致可以分为三类：干涉式测量法、双光电探测器法、光栅光谱仪测量法，其中干涉式测量法因具有实用性和精确性的优点，成为国内外重点研究对象。典型的干涉式激光波长测量有法布里-珀罗干涉法、迈克尔逊干涉法和斐索干涉法。法布里-珀罗干涉法将被测激光和参考激光都锁定至F-P标准具的透射峰值处，通过计算两波长的干涉级次比和拍频测量两波长的波长差值来测得被测激光波长。由于F-P标准具长度固定，虽然波长测量不确定度能达到10-8，但是激光波长测量范围很窄[5-6]。迈克尔逊干涉法通常采用推拉式的光路结构，参考激光器和被测激光器光束同时入射迈克尔逊干涉仪，测量同一光程差下参考激光和被测激光干涉条纹数之比，可得到两光束波长之比。当被测激光和参考激光波长非常接近(比如1 pm)时，需要大大增加导轨运动范围(如运动范围达到475 mm)，或者需要对干涉信号进行高精度细分，这将导致测量系统结构复杂、可靠性差，而且成本很高。此外，该方法的测量精度不仅受限于参考激光器精度，而且易受导轨运动过程中参考激光和被测激光的平行度影响，波长测量不确定度通常为10-7[7-10]。笔者在前期研究中，提出了基于合成波长检测的激光波长测量方法，通过检测被测导轨运动过程中参考激光和被测激光干涉信号的两次同时过零位置来测得合成波长大小，从而计算被测激光波长大小，波长测量不确定度能达到10-7～10-8，但是光路中仍需要参考激光器，测量精度仍受限于参考激光器精度[11-13]。斐索干涉法采用线阵CCD图像传感器，检测待测激光通过斐索标准具后产生的干涉条纹在空间的光强分布，通过计算条纹的周期间隔实现对待测激光波长的测量，该方法虽然不需要参考激光，结构简单，但是由于系统对环境温度变化、机械振动的抗干扰能力差，因此在测量过程中需要实时标定，给使用带来极大不便，测量不确定度为10-6～10-7[14-15]。

本文提出了一种基于单频正交线偏振光的激光波长直接测量新方法，不需要参考激光光源，不仅能够测出干涉条纹变化的整周期部分，还能够测出干涉条纹变化不足一个周期的部分，能实现激光波长的大范围高精度连续直接测量。

1 测量原理

基于单频正交线偏振光的激光波长直接测量系统的光路结构如图1所示，被测激光器输出波长为λu的单频激光经过偏振片P1后形成线偏振光，射向e轴与线偏振光的偏振方向成45°角的1/4波片Q1后形成圆偏振光，该圆偏振光由正交线偏振光组成，其中λu垂直偏振分量射向由分光镜BS1、安装在压电陶瓷驱动器(piezoelectric ceramic transducer，PZT)上的参考镜M1和偏振分光镜PBS1组成的第一套迈克尔逊干涉仪，形成垂直偏振分量的干涉信号，该干涉信号经偏振分光镜PBS2反射后由光电探测器PD1接收；同时λu水平偏振分量射向由分光镜BS1、参考镜M1和测量镜M2组成的第二套迈克尔逊干涉仪，形成水平偏振分量的干涉信号，该干涉信号经PBS2透射后，再经分光镜BS2反射和透射，分别由光电探测器PD2和PD3接收，通过机械移相使PD2和PD3接收到的两路干涉信号相位差为90°。PD1和PD2接收到的干涉信号用于计算小数干涉条纹，PD2和PD3接收到干涉信号用于计算整数干涉条纹。

P1:检偏器；Q1:1/4波片；PBS1-2：偏振分光镜；BS1-2：分光镜；PD1-3：光电探测器；M1-2：角锥棱镜；PZT：压电陶瓷驱动器图1 基于单频正交线偏振光的激光波长直接测量系统的光路结构

记L0为第一套迈克尔逊干涉仪的参考光路和测量光路之间的初始光程差，L1为第二套迈克尔逊干涉仪的参考光路和测量光路之间的初始光程差。则测量开始前，探测器PD1和PD2检测到的垂直和水平偏振分量干涉信号之间的初始相位差为:

(1)

当测量镜M2移动位移ΔL时，第二套干涉仪的参考光路和测量光路之间的光程差变为L1-2ΔL，则两路干涉信号之间的相位差变为:

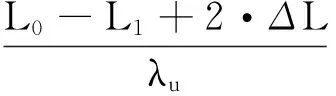
(2)

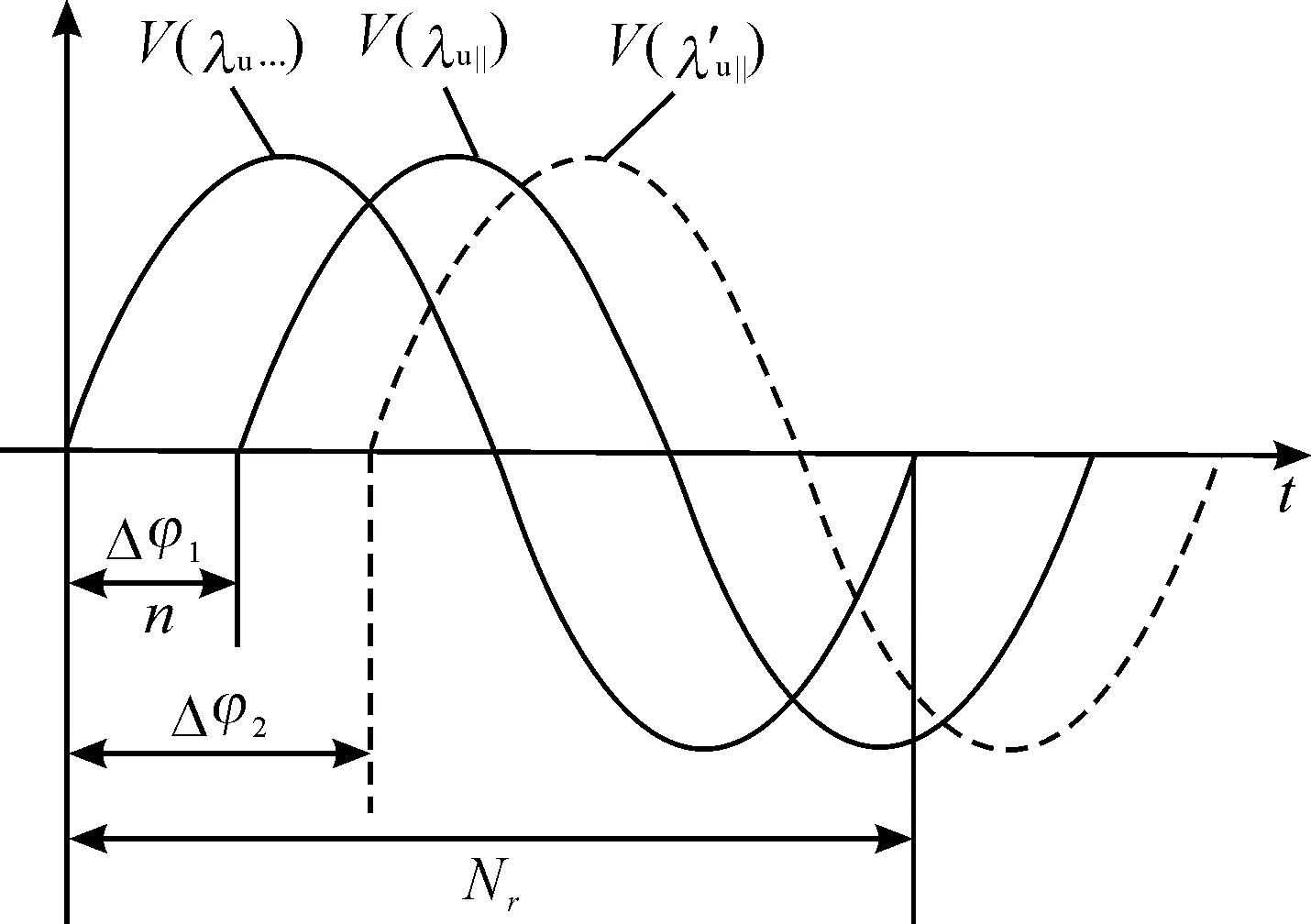
图2 M2移动前后λu垂直偏振分量和λu水平偏振分量干涉信号的相位差变化示意图

当M2移动的位移ΔL超过半个被测激光器波长λu/2时，Δφ2中包含整数个2π，因此式(2)减去式(1)可表示为：

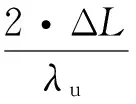
(3)

其中：N为λu水平偏振分量干涉信号相位变化的整周期数，ε为λu水平偏振分量干涉信号相位变化的小数部分，且有：

(4)

其中：Δφ11为测量镜M2运动前V(λu··)与V(λu‖)两路信号之间的相位差，Δφ22为测量镜M2运动后V(λu··)与V(λu‖)两路信号的相位差，Δφ11和Δφ22的范围为0～2π。

因此，在测量镜M2移动前后，通过测量V(λu··)与V(λu‖)两路信号之间的相位差Δφ11和Δφ22计算出小数干涉条纹ε，在M2移动时，测得V(λu‖)的整周期干涉条纹数N，结合式(3)，可计算出被测激光器波长为:

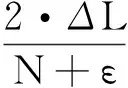
(5)

考虑空气折射率的影响，被测激光器在真空中的波长为：

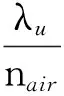
(6)

其中，nair为空气折射率。

2 干涉信号处理

根据上述测量原理可以看出，干涉信号的处理包括：测量镜M2运动时，λu水平偏振分量两路干涉信号的整周期计数；测量镜M2运动前后，λu水平与λu垂直偏振分量两路干涉信号之间的相位差测量。基于可编程逻辑器件(fieldprogrammablelogicarray，FPGA)的干涉信号处理总体框图如图3所示，包括AD7606模数转换、级联积分梳状(cascadedintegralcomb,CIC)数字滤波、整周期干涉条纹计数、小数干涉条纹计数和串行通信等模块。

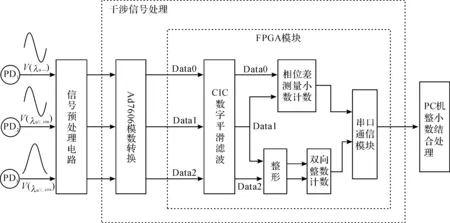
图3 干涉信号处理整体框图

探测器PD1、PD2和PD3测得的三路干涉信号V(λu··)、V(λu‖_sin)和V(λu‖_cos)，经放大、滤波、及电平调零等信号预处理后，峰峰值为±2.5V，分别送至模数转换芯片AD7606的三个模拟量输入端口进行模数转换。AD7606是一个四通道同步采集、16位转换的模数转换芯片，其最高采样频率为200kHz。当AD7606模块进行模数转换时，受电路噪声及外界扰动的影响，A/D转换后的数据会出现抖动，为了消除信号抖动对后续的干涉条纹整数计数和相位测量的影响，在FPGA中利用CIC数字滤波算法分别对采样得到的三路信号Data0、Data1和Data2进行平滑滤波。

测量镜M2运动时，V(λu‖)相位差为90°的两路干涉信号相位变化关系如图4所示。图4(a)中，粗实线表示M2运动时的正弦信号V(λu‖_sin)，细实线表示M2正向运动时的余弦信号V(λu‖_cos)，虚线表示M2反向运动时的余弦信号V(λu‖_cos)。干涉信号经A/D转换后的得到的数据为有符号型整数，采样数据大于等于0时整形输出为1，采样数据小于0时整形输出为0，从而在FPGA内部通过软件将V(λu‖_sin)和V(λu‖_cos)整形为方波，分别用状态量i和j表示。因此在一个干涉条纹周期内，状态量(i, j)有四种组合，即00、01、10、11。如图4(b)所示，如果状态量(i, j)按照01-00-10-11-01规律变化，则表明测量镜M2正向运动，状态量每变化一次，计数器加1；反之如果状态量(i,j)按照00-01-11-10-00规律变化，则表明测量镜M2反向运动，状态量每变化一次，计数器减1。干涉条纹整周期数N为计数器值除以4取整。

图4 整周期干涉条纹计数示意图

根据式(4)，通过检测两路信号Data0和Data1的相位差计算干涉信号V(λx‖)的小数条纹ε。由于图1中两套干涉仪都是单频迈克尔逊干涉仪，在参考镜M1静止不动时，两路干涉信号均为直流信号，为了测得两路干涉信号相位差，通过PZT驱动器调制参考镜M1在12μm范围内往返运动，从而将直流干涉信号调制为图2所示的交流干涉信号。FPGA判断并计算出两路干涉信号相邻正向过零点之间的AD采样点数n，同时计算出V(λu··)一个周期内的采样点数Nr，根据Δφ=n/Nr×360°计算出两路干涉信号之间的相位差。

基于VisualBasic(VB)程序设计的上位机波长测量软件流程如图5所示。波长测量过程中，测量镜M2运动时，测得V(λx‖)干涉条纹变化的整周期数，测量镜M2运动前后，PC机通过VB程序调制参考镜M1测量干涉信号的小数部分ε；最后，根据FPGA经串行通信模块上传的整小数干涉条纹计数结果计算出被测激光波长。

图5 波长测量上位机软件流程

3 实验结果及分析

3.1 波长测量实验

为了验证提出的激光波长直接测量方法的可行性，根据图1搭建了实验平台。如图6所示，激光器采用Renishaw公司生产的ML-10 He-Ne激光器，其波长值为632.992027 nm；参考镜M1选用德国PI公司生产的纳米定位平台P-752.1CD驱动，运动范围为15 μm，分辨率为0.1 nm；测量镜M2的运动由PI公司生产的M531.CD直线位移工作台驱动，运动范围为300 mm，测量镜位移由Aglient 5519A干涉仪提供，5519A干涉仪的测量分辨率为10 nm；采用Altera的EP4CE6F17C8 FPGA开发板，用于测量镜M2运动时V(λx‖)干涉条纹的整周期计数和参考镜调制时V(λu··)和V(λu‖)两路干涉信号的相位差测量。

图6 实验装置照片

实验开始时，测量镜M2静止不动，通过PZT驱动器调制参考镜M1在12 μm范围内往返运动，M1运动速度为200 μm/s，测得V(λu··)和V(λu‖)两路干涉信号的初始相位差为Δφ11；然后测量镜M2运动位移250 mm，测得V(λu‖)干涉条纹变化的整周期值N；M2停止运动后，再次通过PZT调制参考镜M1，测得两路干涉信号的相位差Δφ22。在此过程中，M2的运动位移ΔL的准确值由Aglient 5519A干涉仪测得，同时环境空气折射率nair也由Aglient 5519A干涉仪的折射率补偿单元测得。将测得的Δφ11、Δφ22、N、ΔL和nair代入式(4)和(6)，可计算出被测激光的真空波长值。按以上实验步骤进行了30次重复性实验，共测得30组激光真空波长值，波长测量结果如图7所示。30组重复性实验测得激光波长的平均值为632.991754 nm，测量误差小于0.27 pm，测量不确定度达到4.5×10-7。

图7 ML-10激光器波长测量结果

3.2 测量不确定性分析

根据式(6)可知，被测激光波长测量相对不确定度为：

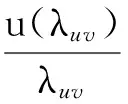
(7)

其中：u(ΔL)为测量镜M2运动位移ΔL的不确定度，u(nair)为空气折射率的测量不确定度，u(N+ε)为干涉条纹整小数计数测量不确定度。

在实验中，Aglient 5519A干涉仪位移测量分辨率为u(ΔL) =10 nm，Aglient 5519A折射率补偿单元测量不确定度u(nair)=5×10-7。测量镜M2运动位移ΔL=250 mm时，u(ΔL)/ΔL=4.0×10-8，当激光器的真空波长λ=632.992027 nm，干涉条纹整数计数值N为790138，PZT驱动器调制参考镜M1运动时，相位差测量不确定度为 0.87°，则u(ε)=0.015，由于干涉条纹整周期计数N不存在误差，因此u(N+ε)=u(ε)= 0.015。将上述参数代入式(7)，可得被测激光波长的相对不确定度为u(λuv)/λuv=5.0×10-7，该分析结果与波长测量结果基本一致。

此外，从上述分析可以看出，被测波长的测量不确定度主要取决于空气折射率的测量不确定度u(nair)。当被测波长在400～1100 nm范围内变化时，u(nair)的值和u(ε)与被测波长无关，基本保持不变。如果测量镜M2运动位移ΔL仍为250 mm，u(ΔL)/ ΔL也保持不变，此时干涉条纹整数计数值N的变化范围是454545～125000，则式(7)中u(N+ε)/N为1.2×10-8～3.3×10-8. 波长测量相对不确定度仍为u(λxy)/λxy= 5.0×10-7。因此，本文提出的波长测量方法能实现激光波长的大范围高精度连续直接测量。

4 结 语

本文提出了一种基于单频正交线偏振光的激光波长直接测量方法，在光路中构建了两套迈克尔逊干涉仪，通过压电陶瓷驱动器调制两套干涉仪的参考镜，将对未知波长的测量转化为干涉条纹信号整周期计数和干涉信号相位差的测量。采用Altera的EP4CE6F17C8 FPGA实现对干涉信号A/D采样、滤波、整形、整周期计算和相位差计算，并结合Agilent5519A干涉仪测得的测量镜移动距离及空气折射率值，计算出被测激光器波长。对He-Ne激光器波长测量实验结果表明，激光器波长测量误差小于0.27 pm，测量不确定度达到4.5×10-7。

[2] VOIGT D, ELLIS J D, VERLAAN A L, et al. Toward interferometry for dimensional drift measurements with nanometer uncertainty[J]. Measurement Science and Technology,2011,22(9):1083-1086.

[3] QUINN T J. Practical realization of the definition of the metre, including recommended radiations of other optical frequency standards(2001)[J].Metrologia,2003,40(2):103-133.

[4] 陈本永,杨万福,严利平.激光频率(波长)测量技术研究现状及发展[J].激光杂志,2009,30(2):1-3.

[5] PARKER T R, FARHADIROUSHAN M. Femtometer resolution optical wavelength meter [J]. IEEE Photonics Technology Letters,2001,13(4):347-349.

[6] 陆宏,姜玲珍,耿完桢,等.利用F-P标准具实时测量激光波长的研究[J].激光技术,1996,20(3):144-146.

[7] 彭月祥,王利强,宁可庆.单片机控制的高精度Michelson干涉型波长计[J].纳米技术与精密工程,2007,5(2):153-156.

[8] WAKIM M, TOPCU S, CHASSAGNE L, et al. Highly accurate laser wavelength meter based on Doppler effect[J]. Optics Communications,2006,262(1):97-102.

[9] HUSSEIN H, SOBEE M A, AMER M. Calibration of a Michelson-type laser wavemeter and evaluation of its accuracy[J]. Optics and Lasers in Engineering,2010,48(3):393-397.

[10] DIZ-BUGARIN J, OUTUMURO-GONZALEZ I, et al. Design of a new microcontroller-based vernier fringe counter for interferometric measurement of laser wavelength[J]. IEEE Transactions on Instrumentation and Measurement,2015,65(2):1-6.

[11] YAN L P, CHEN B Y, YANG W F, et al. A novel laser wavelength meter based on the measurement of synthetic wavelength[J]. Review of Scientific Instruments,2010,81(11):115104.

[12] YAN L P, CHENB Y, ZHANG S H, et al. Laser wavelength precision measurement based on a laser synthetic wavelength interferometer[J]. Review of Scientific Instruments,2016,87(8):3318-4290..

[13] 张岑.激光合成波长干涉波长测量系统设计[D].杭州:浙江理工大学,2015:13-26.

[14] VOLKOV S Y, PEPLIPENKO V I, SMIRNOVV V. Computer-controlled laser radiation wavelength meter based on the Fizeau interferometer[J]. Soviet Journal of Quantum Electronics,1982,12(3):380-381.

[15] 宋建明,是度芳.利用斐索干涉测量激光波长[J].量子电子学报,2001,8(3):224-227.

(责任编辑： 康 锋)

Laser Wavelength Direct Measurement Method Based onthe Single Frequency Orthogonal Polarized Lights

YAN Liping，LIU Pengpeng，XIE Jiandong，CHEN Benyong

(Nanometer Measurement Laboratory, Zhejiang Sci-Tech University, Hangzhou31001, China )

A laser wavelength direct measurement method based on the single frequency orthogonal polarized lights is proposed in this paper. The unknown laser wavelength is achieved by counting the integral fringes and determining the phase difference of two interference signals. Without using a reference laser, the proposed method is able to measure laser wavelength directly with a high accuracy in a wide range. Signal processing method for interference fringe counting is designed based on FPGA. The experimental result of He-Ne laser shows that the wavelength measurement error is less than 0.27 pm and the relative measurement uncertainty is 4.5×10-7. Therefore, the feasibility of the proposed laser wavelength direct measurement and the effectiveness of signal processing method are verified

laser wavelength measurement；interferometer；phase difference determination；FPGA

10.3969/j.issn.1673-3851.2017.09.016

2016-11-06 网络出版日期： 2017-01-19

国家自然科学基金项目(51205365，51475435)；浙江理工大学521人才培养计划

严利平(1977-)，女，四川内江人，副教授，博士，主要从事精密测量技术方面的研究。

陈本永，E-mail：chenby@zstu.edu.cn

TH741

A

1673- 3851 (2017) 05- 0699- 06