空气层对织物热传递影响的模拟分析

张艺强，陈扬，范艳娟，杨允出,b

(浙江理工大学，a.国际教育学院；b.浙江省服装工程技术研究中心，杭州 310018)

空气层对织物热传递影响的模拟分析

张艺强a，陈扬a，范艳娟a，杨允出a,b

(浙江理工大学，a.国际教育学院；b.浙江省服装工程技术研究中心，杭州 310018)

为了分析空气层厚度与位置对织物热传递的影响，利用ANSYS建立3层材料热传递有限元模型。2种模型的空气层分别处于底部(模型1)和中间(模型2)，空气层厚度为1～5 mm，逐渐增加。对织物模型进行一维热传递的数值求解，分析不同条件下多层织物传热过程的温度分布和织物表面的瞬态温度值。结果显示：达到稳态之前，在相同时间点模型1的织物外表面温度要低于模型2；空气层的厚度对织物表面稳态时的温度有影响，随着空气厚度的增加，在相同时间点各模型外表面温度逐渐降低，且下降梯度逐渐变小。进一步通过恒温板实验验证，结果发现织物外表面温度的模拟值与实验值随时间变化的一致性较好，最大相对误差为5.65%。

热传递；空气层；织物；有限元

0 引 言

服装舒适性的研究一直都是焦点，其中热传递是影响纺织品舒适性的重要性能之一，然而在人体与服装之间、服装与服装之间存在着空气,由于空气导热系数远远小于织物的导热系数，所以空气层对人体向外界传递热量有着非常重要的影响。很多学者在空气层对热传递的影响方面做了大量工作。早在1999年Torvid等[1]利用小尺度台式测试，不考虑辐射传热的影响，建立了面料与传感器之间空气层的一维热传递。Talukdar等[2]利用计算流体力学软件将空气层的模拟传热推广到多维。Ghazy等[3]建立面料与空气层的多层组合模型。孙玉钗等[4]通过有限元方法建立纺织品热传递理论模型，模拟得出织物每增加1层、空气层每增加1 mm，织物的热损失减少40%左右。环境温度越低，热损失越多。常生等[5]分析不同厚度和面积的空气层与织物的复合热阻，得出织物与空气层的复合热阻会随着空气层的面积和厚度的增大而增大，并且呈线性关系。李利君等[6]得出增加3 mm的空气层，多层织物系统的总热阻值增加10%左右。段杏元等[7]使用站立式暖汗出汗假人分别对男士发热内衣及纯棉内衣的热阻与湿阻进行了测量，分别建立了2种内衣的空气体积与热阻和湿阻之间的多项回归模型，得出2种内衣的热阻与湿阻均随空气层厚度的增加而增大到最大值，而后再逐渐减小。在消防服上Fu等[8]得出在服装多层系统中不同位置、不同厚度的空气层对服装的热防护性能有不同程度影响。王云仪等[9]通过燃烧假人的三维扫描确定衣下空气层的分布状况，结果显示，在肩部、前胸、大腿和膝盖等部位的空气层较小，在腰、后膝和小腿的空气层相对较大。

本文将用有限元软件对织物与空气层的组合方式以及不同空气层厚度下的织物模型进行传热模拟，探索表面瞬态温度变化的规律，从而为隔热服装的设计以及不同服装的保暖组合方式提供指导。

1 理论研究

在不考虑湿传递的情况下，热量传递方式有：传导、对流和辐射3种。在由人体皮肤-面料-环境构成的服装系统中，皮肤与内层织物、外层织物与环境间的温差很小，并且织物内部纱线与纱线交织形成的孔隙相对较小，在正常情况下，热传导的传热效果远大于对流和辐射对传热的贡献，因此实际中一般不考虑辐射的影响，只考虑导热及对流换热。

当一平壁内部各处的温度是均匀的，等于环境温度T0，如图1中BH所示。在AB侧给定一恒定温度T1，右侧仍然与环境接触，这时靠近左侧的部分温度会很快上升，其余部位依然保持初始温度T0，随着时间的推移，平壁各部分温度逐渐升高，右侧表面温度也逐渐升高，如图1中曲线AC、AD、AE、AF所示，最终达到稳定，如AG所示。此时热量传递遵循能量守恒定律及傅里叶定律[10]:

(1)

式中：T为温度，℃；t为时间，s；λ为导热系数，W/(m·K)；ρ为质量密度，kg/m3；c为比热，J/(kg·℃)。

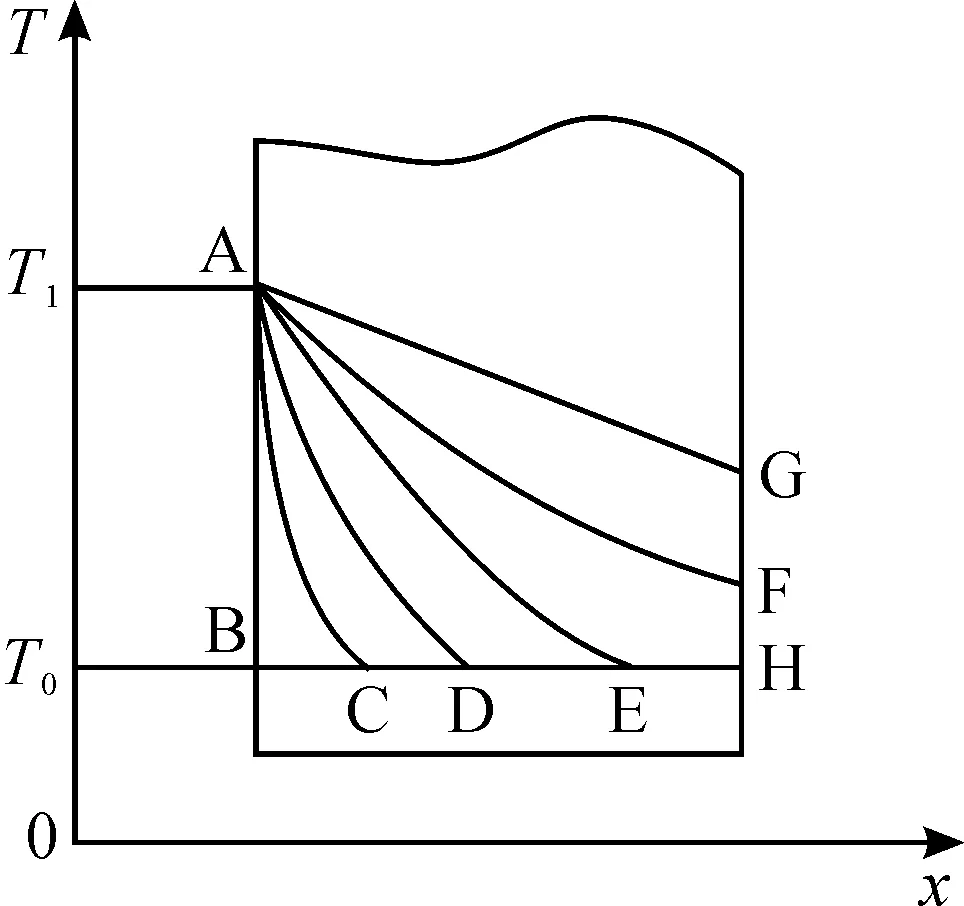
图1 非稳态导热温度分布

织物表面与环境接触存在对流换热。对流换热是指流体流经固体时流体与固体表面之间的热量传递现象，如图2所示。可用牛顿冷却方程描述：

(2)

其式中：q*为热流密度，W/m2；hf为对流换热系数，(W/m-2·K-1)；Tb为固体表面的温度，℃；Ts为周围流体的温度，℃。

图2 对流示意图

2 模拟研究

织物的热传递是一个复杂的过程，为了简化问题，这里把它作为一种匀质平板[11]材料，其传热过程为：人体皮肤散发的热量通过“小气候”、织物、织物间空气层及织物表面的边界层空气传递至外界环境。将织物内部结构与纱线空隙间的空气当成一个整体考虑，用其总导热系数作为导热参考量，织物和空气的比热容及质量密度作为常量，建立人体皮肤到环境的热传递模型。简化模型如图3所示，箭头为热量传递方向。

图3 带空气层的多层织物热传递模型

2.1 参数条件

环境温度为21.8 ℃，模拟与实验采用的面料为纯棉平纹布，参数如表1所示。

表1 纯棉平纹布与空气导热参数

注：面料经密：180根/10 cm，纬密：170根/10 cm。

模型边界条件：对流换热系数为10 W/(m2·K)；人体皮肤温度假定为33.6 ℃。

2.2 有限元模型及处理

不同空气层位置与厚度的一维简化几何模型如图4所示。模型1:皮肤-空气层-面料-面料-环境;模型2:皮肤-面料-空气层-面料-环境，空气层厚度在1～5 mm区间变化。在ANSYS有限元软件中建立各织物与空气层的组合模型后，添加温度载荷和环境条件，假设织物上表面与环境发生对流换热，内部空气层为静止的。在ANSYS中统一以m为单位。采用手动映射网格划分，网格单元尺寸为0.0001 m。图5为织物与空气层的网格模型。图6为稳态条件下模型1(3 mm空气层厚度，环境温度为21.8 ℃)的最终温度分布云图。图6中MX和MN分别表示最大值和最小值。

图4 不同空气层位置与厚度的简化几何模型

图5 网格模型

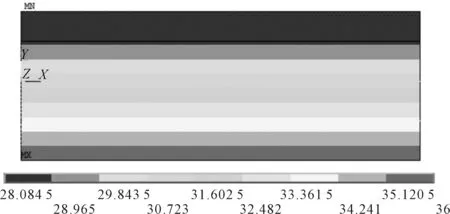
图6 模型1(3 mm空气层)的温度分布云图

2.3 结果分析

本次模拟采用瞬态热传导分析，时间总历程为200 s,步长为1 s，最大步长为2 s。2种模型分别模拟了在表面对流换热不变的情况下，环境温度为21.8 ℃时，模型表面热量传递过程中的温度变化。图7给出了模型1和模型2在不同空气层厚度条件下的织物表面温度随时间的变化曲线。

图7 不同模型中织物表面温度时间曲线

a) 空气层厚度对织物热传递的影响

如图6所示，将模型2中的空气层以1 mm为梯度，逐渐增加到5 mm，用有限元软件分别模拟5个空气厚度下的热传递，提取织物表面温度变化如图7所示。随着空气厚度的增加，在相同时间点各模型外表面温度逐渐降低，且下降梯度逐渐变小。空气层厚度从1 mm增加到2 mm时，织物表面温度差为1.955 ℃，依次从2 mm增加到3 mm、3 mm增加到4 mm、4 mm增加到5 mm时的温度差值为1.290、0.914和0.683。

b) 空气层位置对织物热传递的影响

在外界环境条件相同的情况下，在热传递达到稳态之前，空气层的位置对织物热传递有影响，在相同时间点空气层位于底部的织物模型外表面温度要低于空气层位于中间的织物模型，如表2所示。在传热达到稳态时，模型1和模型2的外表面温度相同，空气层的位置对模型稳态时的表面温度没有影响。

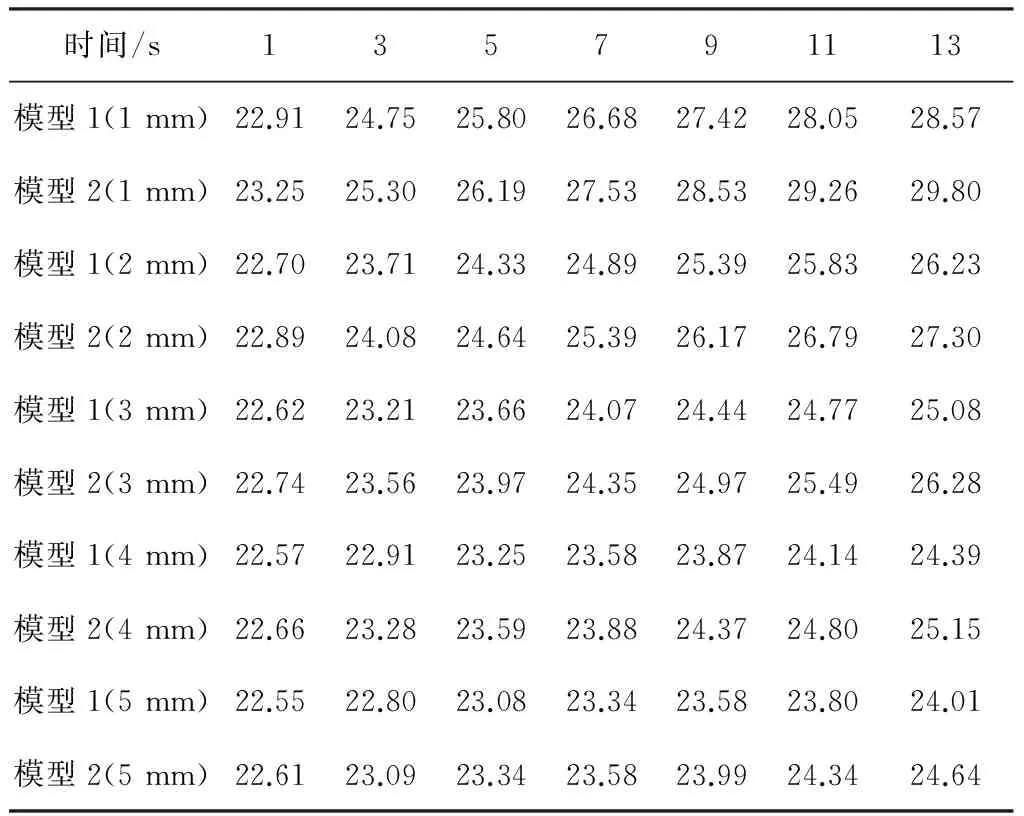
表2 不同模型的表面温度 ℃

3 实验验证

为了验证模拟结果的准确性，在人工气候室中进行实验。所用面料参数见表1。实验设备主要包括恒温加热平台，PT100温度传感器，亚克力板。用恒温加热台给定恒定温度，平台设定为36.0 ℃,此时平台表面温度实测为33.6 ℃±0.2 ℃，恒温平台发热面积20 cm×20 cm。亚克力板的厚度从1～5 mm，中间挖出10 cm×10 cm的方形用于模拟空气层厚度。实验过程中，试样按图6的不同模型进行放置，采用PT100温度传感器获取织物表面瞬态温度。每组实验做3次，取3次的平均值。有限元模拟数据与实验数据对比结果如图8和图9所示。

图8 模型1不同空气厚度下模拟和实验散点图

图9 模型2不同空气厚度下模拟和实验散点图

由图8和图9可知，模拟分析结果与实验结果最大相对误差为5.65%，用SPSS进行Wilcoxon符号秩检验，在显著性水平0.05下，各组概率p值均大于0.05，模拟值与实验值没有显著差异。实验中，由于恒温平板的加热精度以及温度传感器的灵敏度会导致误差，此外，环境气候也存在一定范围的波动，对流换热系数的确定是非常复杂的，现实环境的对流并没有模拟中的那么稳定，也会引起理论数据与实验数据的偏差。

4 结 论

本文通过模拟织物热传递，得出以下结论:

a) 通过有限元软件ANSYS模拟真实环境条件下温度在织物中的传递,可提取出织物横截面任意位置、任意时刻的瞬态温度分布情况。

b) 在外界环境条件相同的情况下，空气层的位置对模型表面稳态温度没有影响。但在热传递达到稳态之前，空气层的位置对织物热传递有影响，在相同时间点、空气层位于底部的模型外表面温度要低于空气层位于两面料之间的模型温度。

c) 随着空气厚度的增加，在相同时间点各模型外表面温度逐渐降低，且下降梯度逐渐变小。

[1] TORVID A, DALEJ D, FAULKNER B. Influence of air gaps on bench-top test results of flame resistant fabrics[J]. Journal of Fire Protection Engineering,1999,10(1):1-12.

[2] TALUKDAR P, TORVI D A, SIMONSON C J, et al. Coupled CFD and radiation simulation of air gaps in bench top protective fabric tests[J]. International Journal of Heat and Mass Transfer,2010,53(1):526-539.

[3] GHAZY A, BERGSTROM D J. Numerical Simulation of heat transfer in firefighters protective clothing with multiple air gaps during flash fire exposure[J]. Numerical Heat Transfer, Part A: Applications,2012,61(8):569-593.

[4] 孙玉钗,冯勋伟,程中浩.空气层及织物层数对通过纺织品热量损失的影响[J].纺织学报,2005,26(2):74-76.

[5] 常生,李津.空气层对针织物热传递性能的影响[J].针织工业,2015(7):100-103.

[6] 李利君,宋国文,李睿,等.消防员防护服面料的热湿舒适性[J].纺织学报,2017,38(3):122-125.

[7] 段杏元,胡源盛.男性针织内衣热性能的测量与分析[J].纺织学报,2016,37(12):92-96.

[8] FU M, WENG W, YUAN H. Effects of multiple air gaps on the thermal performance of firefighter protective clothing under low-level heat exposure[J]. Textile Research Journal,2014,84(9):968-978.

[9] 王云仪,张雪，李小辉，等.基于Geomagic软件的燃烧假人衣下空气层特征提取[J].纺织学报,2012,33(11):102-106.

[10] 秦臻.传热学理论及应用研究[M].北京:中国水利水电出版社,2016:33-36.

[11] FAN J T, LUO Z X, LI Y. Heat and moisture transfer with sorption and condensation in poros clothing assembilies and numerical simulation[J]. International Journal of Heat and Mass Transfer,2000,43:2898-3000.

(责任编辑： 唐志荣)

Simulation Analysis of the Influence of Air Layeron Fabric Heat Transfer

ZHANG Yiqianga, CHENG Yanga, FAN Yanjuana, YANG Yunchua,b

(a.International Education College; b.Zhejiang Provincial Research Center of Clothing Engineering Technology, Zhejiang Sci-Tech University， Hangzhou 310018， China)

To analyze the influence of air layer thickness and position on heat transfer of fabric, a 3-layer material heat transfer finite element model was built with ANSYS system. The air layer of two models is at the bottom (model 1) and the middle (model 2) respectively, and the air layer thickness ranges from 1 to 5 mm (taking on an increase trend). Numerical values of one-dimensional heat transfer were calculated to analyze the distribution of temperature of multilayer fabric system in the heat transfer process under different conditions and the transient temperature of fabric surface nodes. The results show that, before the steady state is reached, the fabric outer surface temperature in model 1 is lower than that in model 2 at the same time point; the air layer thickness has an influence on fabric surface temperature in the steady state, and the outer surface temperature of the models gradually decreases at a decreasing rate at the same time point with the increase of air thickness. Further experiment with thermostatic plate shows that the simulation value and experimental value of outer surface temperature of fabrics are highly consistent with each other, with a maximum relative error of 5.65%.

heat transfer; air layer; fabric; finite element

10.3969/j.issn.1673-3851.2017.09.002

2017-5-11 网络出版日期： 2017-08-07

浙江省自然科学基金项目(Y17E060034)；浙江理工大学教育教学改革研究项目(jgyl1403)

张艺强(1992-)，男，江苏宿迁人，硕士研究生，主要从事服装舒适性与功能方面的研究。

杨允出，E-mail：gary0577@zstu.edu.cn

TS101.1

A

1673- 3851 (2017) 05- 0616- 05