环形编织纱线间接触作用对编织增强体结构参数影响研究

迟进佳，周 强，吴震宇

(浙江理工大学机械与自动控制学院，杭州 310018)

环形编织纱线间接触作用对编织增强体结构参数影响研究

迟进佳，周 强，吴震宇

(浙江理工大学机械与自动控制学院，杭州 310018)

编织增强体结构参数是影响复合材料力学性能的关键因素，而在环形编织中纱线间接触作用对编织增强体结构参数会产生影响。采用连续杆单元对柔性纱线进行建模，设定符合实际情况的边界条件及材料参数，对编织过程进行有限元仿真。通过实验验证理论分析和有限元仿真结果的有效性。对有限元仿真结果和实验结果对比分析，总结得出不同纱线摩擦系数、纱线张力、纱线接触点数量对编织增强体结构参数编织角影响规律：当纱线摩擦系数较大时，编织过程中纱线出现更明显偏移，编织增强体编织角小于理论设定值；当纱线所受张力增大时，编织增强体编织角更接近于理论设定值；编织过程中使用的纱线数量增多时，纱线接触点数量增多，彼此间相互接触作用影响增强，使编织角小于理论设定值。

环形编织；纱线相互接触；有限元仿真；编织增强体

0 引 言

环形编织技术通常用于制备中空结构的纤维增强体复合材料零部件，目前已经大量应用于航空航天领域和汽车行业[1-3]。环形编织增强体中纱线的走向决定其几何结构，编织增强体几何结构对复合材料力学性能有重要的影响，因此确定纱线的合理走向十分重要。编织增强体编织角是表征纱线走向重要的参数。Ko[4]根据卷取速度v与线轴旋转角速度ω之间关系推导出规则芯轴时编织角理论值计算公式。Popper[5]在Frank规则形状芯轴基础上，对非规则形状芯轴编织增强体编织角进行了求解。Zhang[6-7]通过建立纱线的运动学和力学模型，分析了编织过程中纱线的运动状态。Na等[8]和Akkerman等[9]分别建立了不同的数学模型来模拟纱线在编织芯轴表面走向，但由于没有考虑纱线间相互接触作用，导致所得结果与实际编织结果存在一定偏差。

本文首先介绍环形编织的过程，对编织增强体结构参数编织角进行了说明。其次对纱线在集中区域内接触受力进行分析，总结出导致编织角变化的原因及三个主要影响因素：纱线张力、纱线摩擦系数、纱线接触点数量。然后分别用有限元仿真和实验对上述影响因素进行分析。结合有限元数值模拟结果和实测实验结果，得出不同纱线张力、纱线摩擦系数、纱线接触点数量对编织增强体结构参数编织角影响规律，为进一步提高编织增强体复合材料结构参数准确性提供理论参考。

1 环形编织原理

1.1 编织过程

环形编织机主要由编织芯轴、导向环、线轴平台以及安装在线轴平台上编织线轴等组成，其示意图如图1所示。编织纱线一端由安装在线轴平台上的线轴带动，另一端穿过导向环固定在芯轴上。绕芯轴顺时针方向运动的一组纱线为经纱，逆时针运动的另一组为纬纱，两者的角速度分别为±ω。线轴在编织平台上沿“8”字形轨道以上下交替的方式通过，使两组纱线互锁，如图2所示。卷取机构牵引芯轴以速度v做水平运动。在各部分协同作用下纱线在芯轴表面上相互交织，形成闭合的双轴向编织增强体。

图1 环形编织示意图

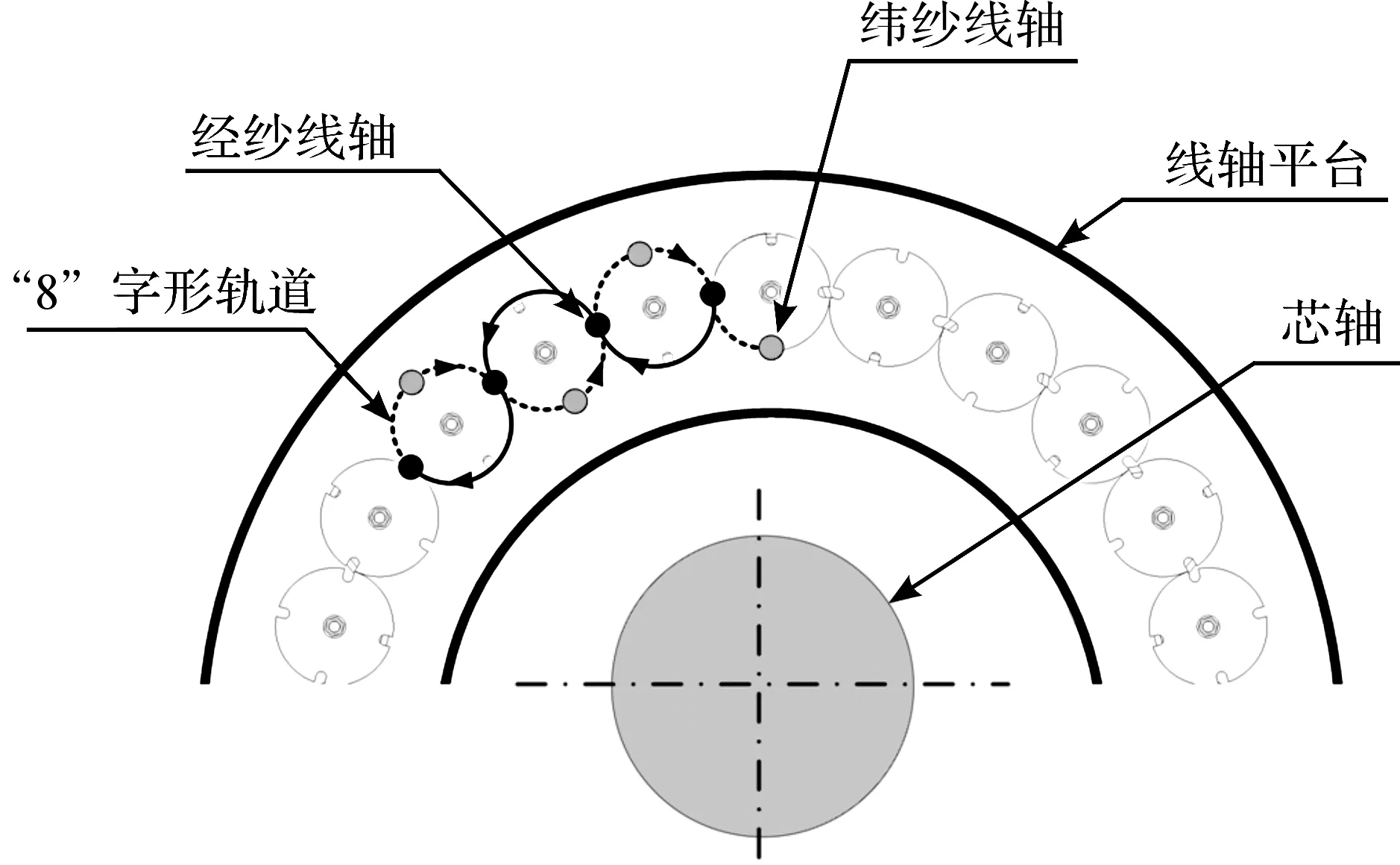
图2 线轴“8”字形轨道

1.2 编织增强体编织角

编织角(α)是最直观反映编织增强体结构的参数，表明纱线的走向，决定编织增强体结构，从而影响编织增强体力学性能，编织角示意图如图3所示。

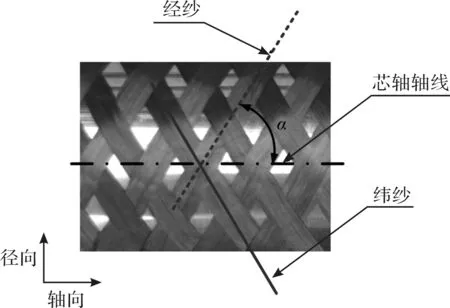
图3 编织角示意图

编织增强体理论编织角可由式(1)计算：

(1)

其中：R为芯轴半径，cm；ω为线轴旋转角速度，r/min；v为芯轴卷取速度，mm/s；C为芯轴周长，mm。

2 纱线间接触作用

2.1 纱线理想运动状态

在研究编织过程中纱线运动时，文献[8-9]为简化计算建立三个基本假设：a)当纱线附着在芯轴表面时不产生滑移；b)纱线在线轴出口至芯轴表面落点之间保持直线状态，忽略纱线间相互接触作用影响；c)纱线在芯轴表面上保持连续。

基于上述假设，纱线在编织集中区域内呈理想状态。取其中一根纱线单独分析，如图4所示，因为不受到相向运动纱线的接触作用，该纱线在集中区域内保持直线状态，且纱线附着在芯轴表面后不会产生滑移。因此根据理想化假设求得编织增强体编织角的值与理论值不存在偏差。

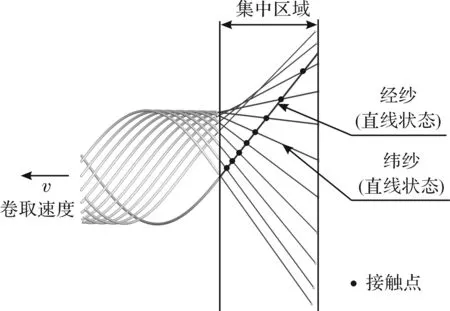
图4 编织过程中纱线理想状态

2.2 纱线实际运动状态

Popper[5]研究发现，实际编织增强体测量编织角始终小于其理论值。经分析认为纱线在集中区域内相互接触作用较为剧烈不能进行忽略。在编织过程中，经纱纬纱彼此相互接触并产生作用力，如图5所示，在集中区域内纱线主要受三个力作用：

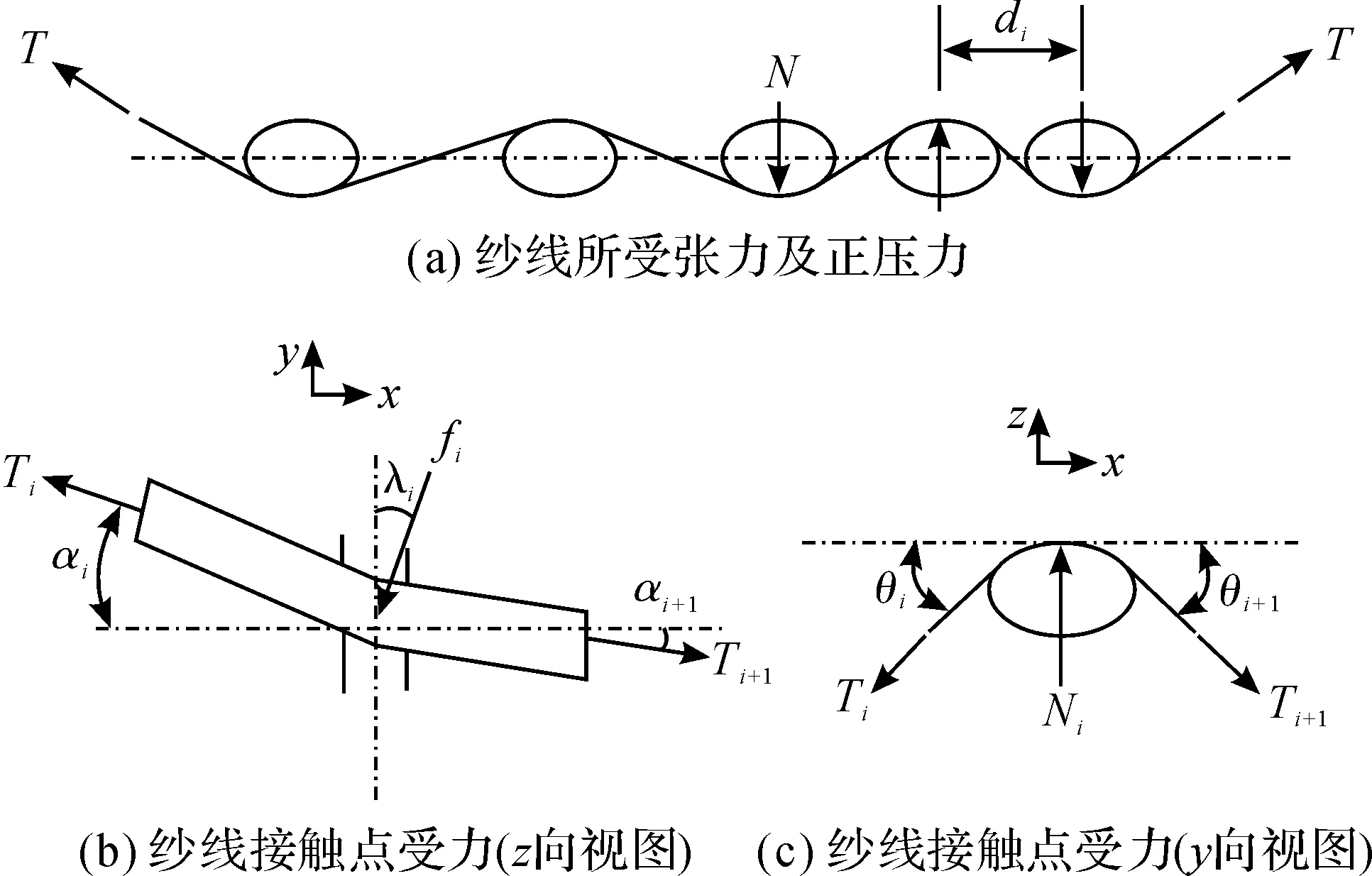
图5 纱线受力示意图

a)纱线张力T,纱线受张力使纱线绷紧且使纱线彼此挤压产生正压力。

b)正压力N,正压力使经纱和纬纱垂直方向位置发生一定变化。

c)纱线间摩擦力f,由于纱线间存在正压力且有相对运动，因此根据库伦摩擦公式f=μN可求得纱线间某一接触点摩擦力。

纱线的一个接触点i在x、y和z三个方向受力平衡方程如下所示：

a) 当Fx=0时：

-Ticosαi+Ti+1cosαi+1-fisinλi=0

(2)

b) 当Fy=0时：

Tisinθi-Ti+1sinαi+1-ficosλi=0

(3)

c) 当Fz=0时：

Tisinθi+Ti+1sinθi+1-Ni=0

(4)

其中αi和αi+1为z向视图中接触点两侧纱线与x轴夹角；θi和θi+1为y向视图中接触点两侧纱线与x轴夹角。

在三个力作用下，编织过程中纱线实际状态如图6所示，纱线在集中区域内不能够保持直线状态，而是产生了一定的弯曲偏斜，导致纱线在芯轴表面的点B由理想位置滑移到点B′。

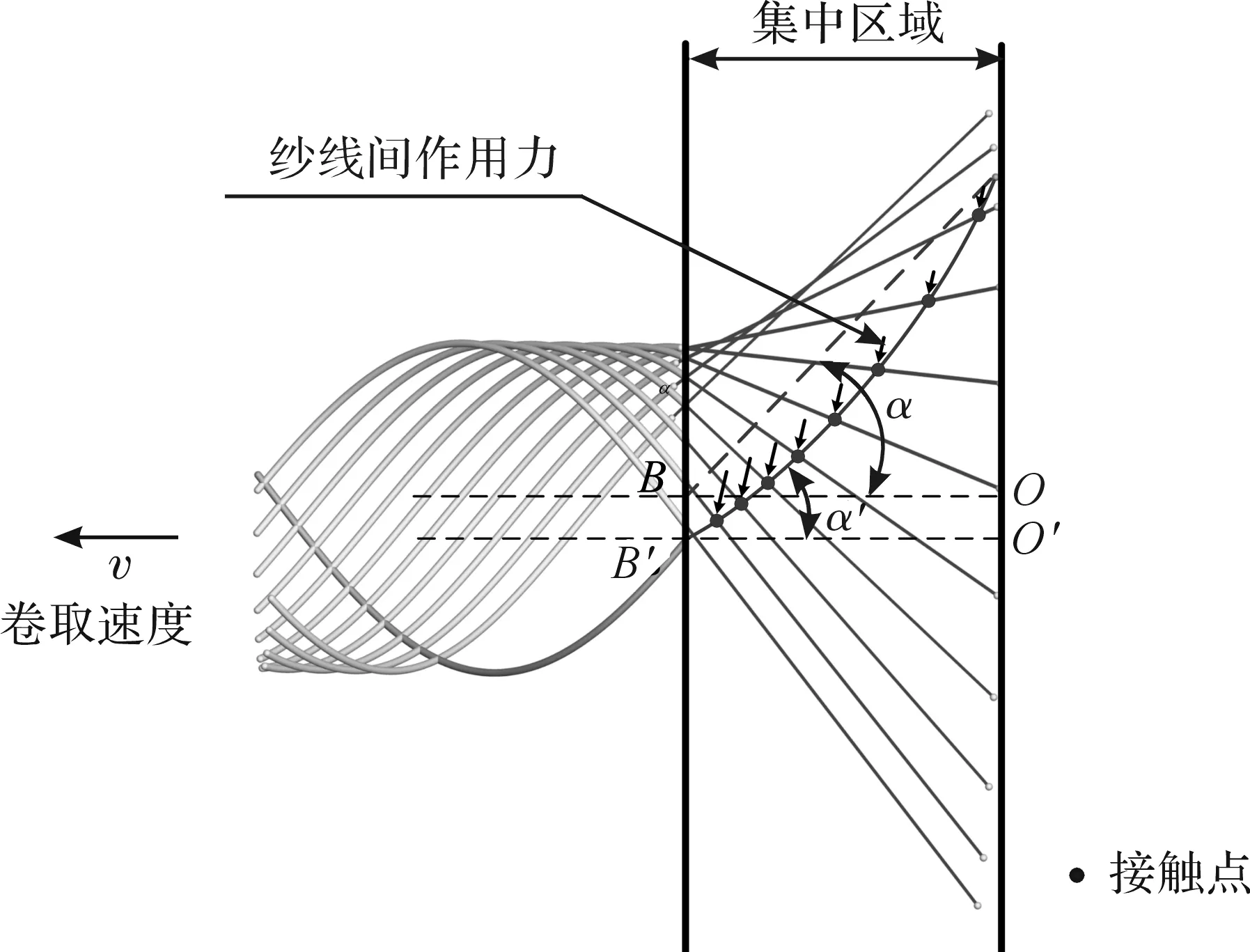
图6 编织过程中纱线实际状态

经上述分析发现，接触作用导致纱线产生偏移弯曲进而引起编织增强体编织角发生变化，总结出其主要影响因素有：a)纱线张力；b)纱线摩擦系数；c)纱线接触点数量。

3 基于ABAQUS有限元仿真

3.1 仿真模型构建

根据实际编织情况构建有限元仿真模型，如图7所示。该模型主要由编织纱线、纱线导向环和编织芯轴三个部分组成。

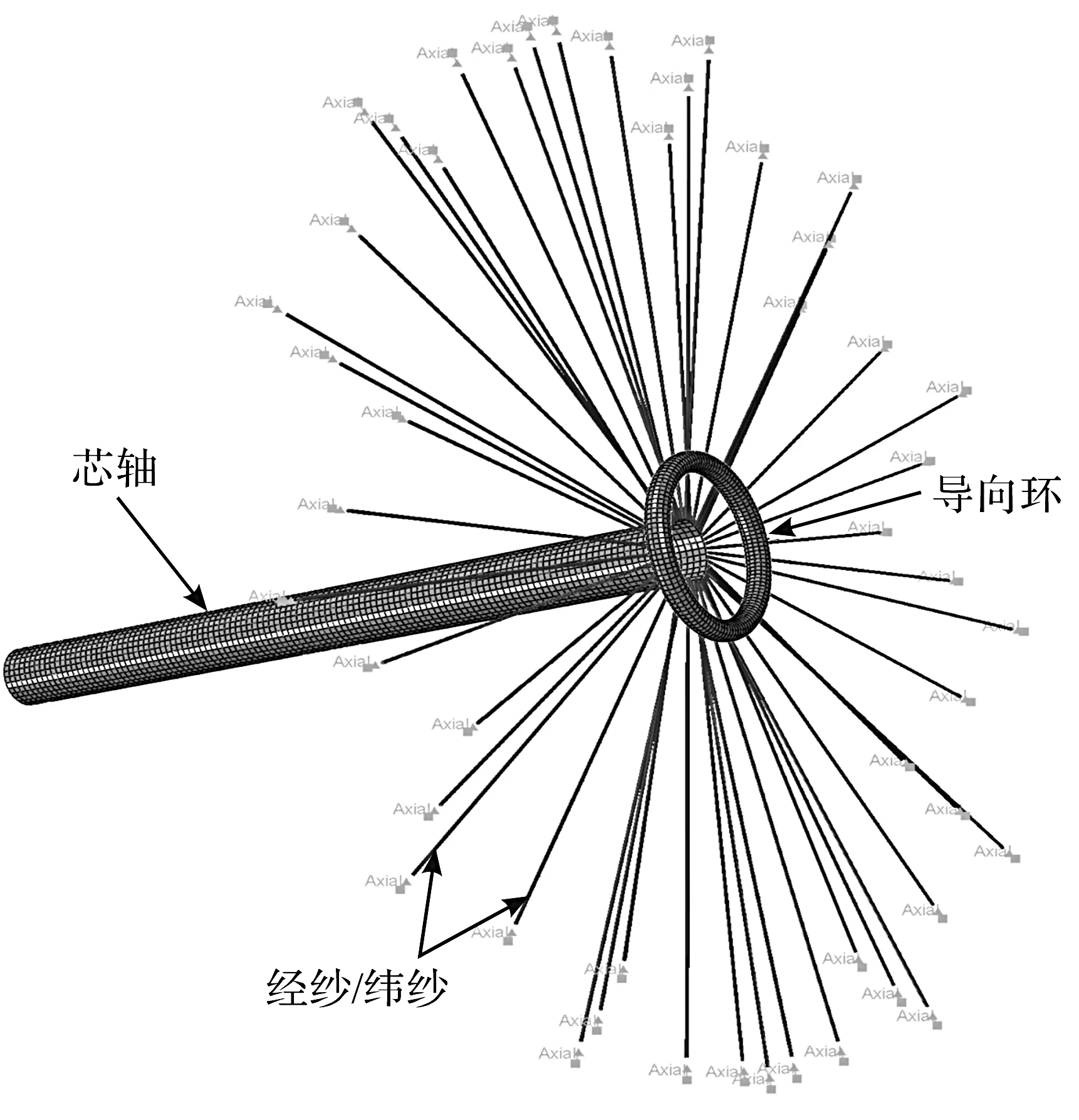
图7 环形编织有限元模型

编织过程中芯轴和导向环通常不会发生变形，因此模型中使用刚体单元。纱线模型是仿真中关键部分，其在具有一定柔性同时需要有较高拉伸强度。根据有限元离散化思想，将纱线离散成若干杆单元[10-12]，为保证纱线模型保持真实纱线柔性，杆单元通常划分较小且数量较多，经过无摩擦可自由旋转铰链进行连接，如图8所示。

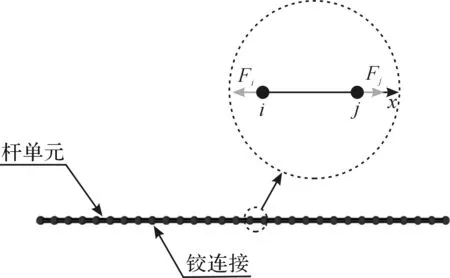
图8 纱线杆单元模型

组成纱线模型杆单元遵循如下四条基本原则：a)杆单元为圆形恒定截面细长杆；b)应力在截面上均匀分布；c)构成杆单元材料满足胡克定律；d)杆单元受力只能沿着中心线方向，不能受到弯矩或者垂直于中心线力。

杆单元刚度矩阵K：

(5)

其中：E为纱线弹性模量，MPa；L为杆单元长度，mm；A为杆单元横截面积，mm2。

在局部坐标系中杆单元平衡方程[10]：

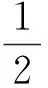
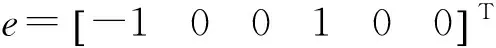
3.2 模型参数及边界条件

设定合理的仿真模型边界条件，将导向环所有自由度约束固定，芯轴按照设定的卷取速度做水平匀速运动。其中较为复杂的是线轴沿“8”字形轨道运动的设定，需将线轴类似于正弦曲线运动轨迹拆分为绕芯轴转动圆周运动和上下起伏周期性运动。有限元仿真中需要设定的主要参数如表1所示。

表1 环形编织有限元仿真参数

在ABAQUS软件中定义纱线与纱线、 纱线与芯轴和纱线与导向环之间的接触算法，各部分间摩擦系数需要根据材料真实属性进行设置。ABAQUS求解器中所涉及到计算时间步长、网格大小等参数依据实际情况进行调试和更改，以提高运算效率跟稳定性。仿真中采用的纱线材料属性见表2。

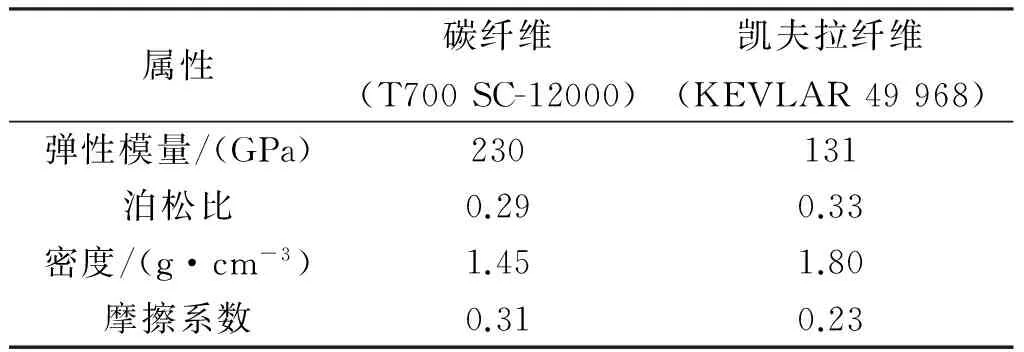
表2 纱线材料属性

3.3 动力学求解方程

本文中有限元仿真选用ABAQUS/Explicit显式动力学求解模块，该模块可用于处理大几何变形和复杂接触问题，采用中心差分算法[13]。

可根据式(7)-(8)将单元节点加速度和速度用其位移表示：

(7)

(8)

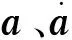
t时刻运动方程为：

(9)

其中M为质量矩阵、C为阻尼矩阵、Fext为节点所受外力向量。

将式(7)和式(8)代入式(9)中，可得到中心差分法的递推公式：

(10)

根据已求得的at-Δt和at，可以进一步得出at+Δt。

3.4 仿真结果及其后处理

经计算得到的仿真结果整体视图及局部细节如图9所示，经纱和纬纱均匀交织附着于芯轴表面，仿真结果与实际所得编织增强体有较高的吻合度。

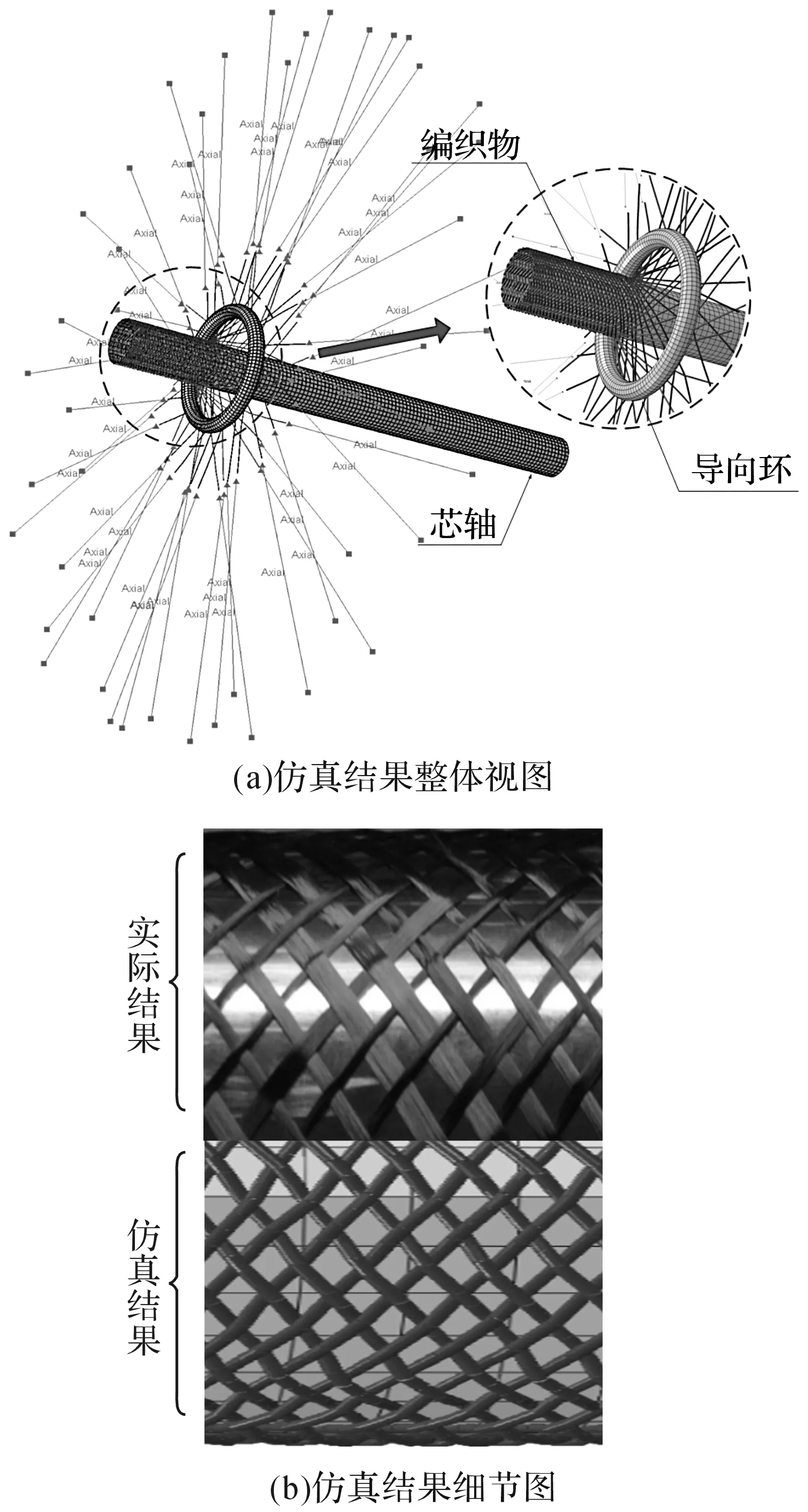
图9 仿真结果整体及细节图

对仿真结果进行处理，提取仿真编织增强体编织角。由于编织纱线采用杆单元链模型，每根纱线由很多根杆单元构成，所以将每根杆单元转换成向量形式，如图10所示。

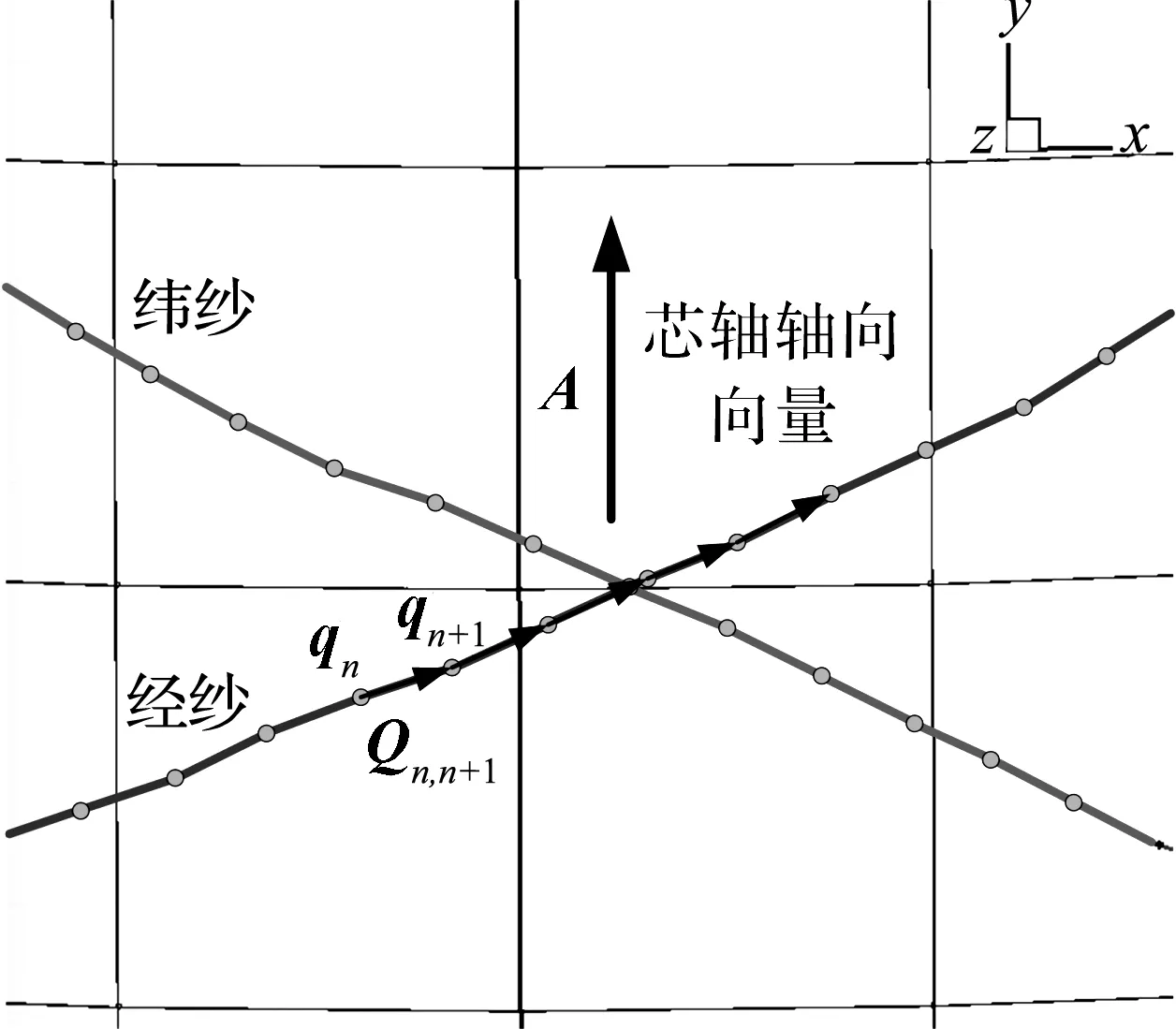
图10 芯轴表面纱线杆单元向量形式

相邻两单元节点构成向量可由式(11)表示：

Qn,n+1=qn+1-qn

(11)

该模型采用是规则的圆柱芯轴，因此容易求得芯轴轴向向量A。纱线编织角理论上可通过求解向量A与Qn,n+1之间夹角得出。但是由于编织增强体中纱线不是紧贴在芯轴表面而是彼此交错上下穿过，导致杆单元方向也随之上下起伏变化。如图11所示，当杆单元上下起伏时，根据计算A与Qn,n+1之间夹角求得的编织角α2大于真实编织角α。

图11 编织纱线上下起伏引起编织角变化

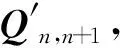
(12)

4 实验及结果分析

4.1 实验设计与结果

通过实验验证上述理论分析和有限元仿真结果的有效性。搭建了如图12所示的48线轴环形编织机实验平台，进行如下3项验证实验：

a)使用不同摩擦系数两种纱线(碳纤维T700、凯夫拉纤维KEVLAR49)，验证当纱线摩擦系数不同时对于编织增强体编织角影响；

b)通过变换张力弹簧调节纱线张力，进行张力对编织增强体编织角影响实验；

c)在纱线种类和纱线所受张力相同前提下，调整纱线数量，研究纱线接触点数量对编织角的影响。

图12 环形编织实验平台

实验根据调节不同的参数得到多组编织增强体实验结果，并使用拓印法获取编织增强体纱线走向，通过多次测量取平均值测得编织增强体编织角，实验结果及测量如图13所示。

图13 实验结果及编织角测量

4.2 结果分析

在纱线张力和数量相同的前提下，使用不同摩擦系数的纱线进行仿真与实验，其结果如图14、图15所示。当选用摩擦系数为0.31的T700碳纤维时编织增强体编织角的仿真值和实验值均比理论编织角偏小3.0°～4.0°，而选用摩擦系数为0.23的KEVLAR49凯夫拉纤维时编织增强体编织角仿真值与实验值均比理论编织角偏小1.0°～2.0°。首先实验值与仿真值吻合程度较高，说明有限元模型具有较高准确度和有效性。其次两者实验值和仿真值均小于理论值，这与纱线间相互作用会导致编织增强体编织角偏小的分析相符。并且当纱线摩擦系数越小时编织增强体编织角越接近理论编织角。

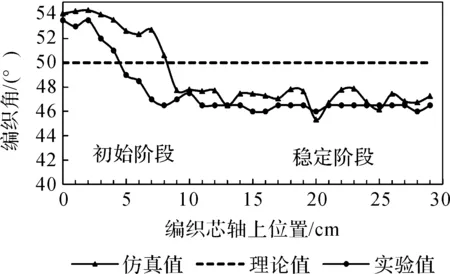
图14 48根碳纤维T700编织角(张力弹簧线径Φ=0.5mm)

图15 48根凯夫拉纤维编织角(张力弹簧线径Φ=0.5mm)

增大仿真中纱线张力值，并据此将实验中将张力弹簧更换为线径Φ=0.7mm弹簧，实验与仿真结果如图16所示。将图14与图16结果进行对比可知当纱线所受张力增大时实验值、仿真值和理论值更为接近，因此在编织中适当增大纱线张力可获得质量更高的编织增强体。

图16 48根碳纤维T700编织角(张力弹簧线径Φ=0.7mm)

当使用24个编织线轴进行编织时所得结果如图17所示，通过与相同纱线和张力使用48个编织线轴的结果对比可知在纱线接触点数量越多情况下纱线相互接触作用越剧烈，编织增强体编织角的仿真值、实验值和理论编织角差别越大。因此当编织纱线数量较多时需对编织工艺参数进行调整，以保证编织增强体的质量要求。

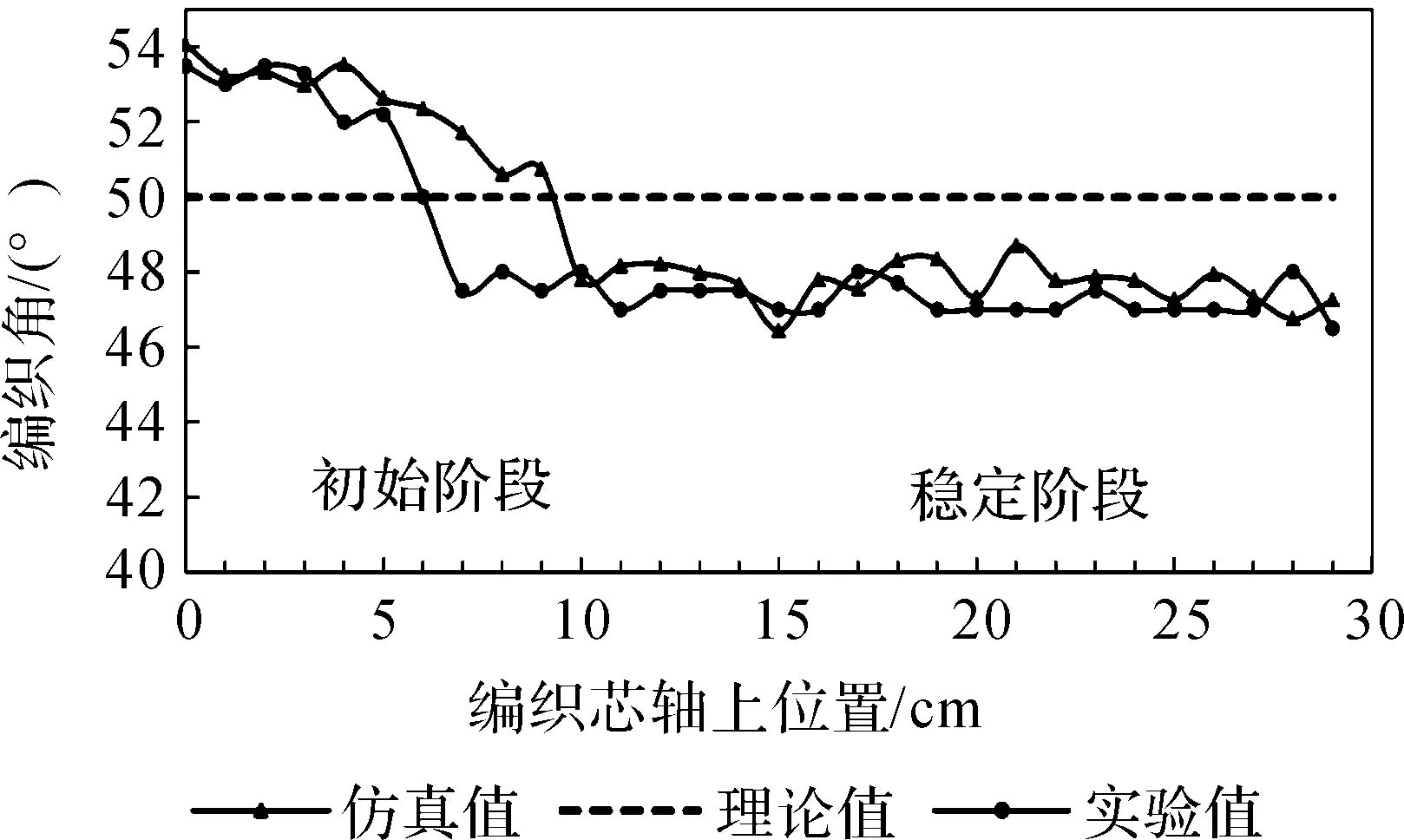
图17 24根碳纤维T700编织角(张力弹簧线径Φ=0.5mm)

5 结 论

本文对环形编织纱线间接触作用影响编织增强体结构参数问题进行了有限元仿真和实验研究， 并分析总结出3种因素对编织增强体结构参数编织角的影响规律：

a)纱线摩擦系数越大时相互接触作用越剧烈，导致编织增强体编织角偏离理论设定值的程度越大；

b)编织纱线张力较大时编织角越接近于理论值，编织过程中应适当增大纱线张力以提高增强体品质，但不能过大以免导致纱线崩断降低生产效率；

c) 当编织过程中使用的纱线数量较多时，纱线接触点数量增多，彼此间相互接触作用影响增强，使编织角小于理论设定值。

[1] KYOSEV Y. Braiding Technology for Textiles: Principles, Design and Processes[M]. Woodhead Publishing,2014:175-194.

[2] 孙志宏,阮谷萍.圆形编织法工艺参数对编织物结构影响[J].纺织学报,1999,20(6):359-362.

[3] 汪星明,邢誉峰.三维编织复合材料研究进展[J].航空学报,2010,31(5):914-927.

[4] KO F.K. Engineered Materials Handbook 1 [M]. USA: ASM International,1987:519-528.

[5] POPPER P. Analysis of a circular braiding process for complex shapes [J]. Journal of the Textile Institute,1994,85(3):316-337.

[6] ZHANG.Q. Analysis of circular braiding process, part 1: Theoretical investigation of kinematics of the circular braiding process [J]. Manufacturing Science and Engineering,1999,121(3):345-350.

[7] ZHANG Q. Analysis of circular braiding process, part 2: Mechanics analysis of the circular braiding process and experiment [J]. Manufacturing Science and Engineering,1999,121(3):351-359.

[8] NA W J, AHN H C, JEON S Y, et al. Prediction of the braid pattern on arbitrary-shaped mandrels using the minimum path condition [J]. Composites Science & Technology,2014,91:30-37.

[9] AKKERMAN R, RODRíGUEZ B. Braiding simulation and slip evaluation for arbitrary mandrels[C]. 10th Esaform Conference on Material Forming, Zaragoza (Spain): American Institute of Physics,2007:1074-1079.

[10] WANG Y, SUN X. Digital-element simulation of textile processes [J]. Composites Science & Technology,2001,61(2):311-319.

[11] ZHOU G, SUN X, Wang Y. Multi-chain digital element analysis in textile mechanics [J]. Composites Science & Technology,2004,64(2):239-244.

[12] PICKETT.A. Comparison of analytical and finite element simulation of 2D braiding [J]. Plastics, Rubber and Composites,2009:387-395.

[13] 王勖成,邵敏.有限单元法基本原理和数值方法[M].2版.北京:清华大学出版社,1997:468-520.

(责任编辑： 唐志荣)

Study about Infleunce of Yarn Contact Effect on StructuralParameter of Knit Reinforcement

CHI Jinjia, ZHOU Qiang , WU Zhenyu

(Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

Structural parameter of knit reinforcement is a key factor influencing mechanical properties of composites. In circular knit, yarn interaction will influence structural parameter of knit reinforcement. Continuous rod unit was used to model flexible yearns. The boundary conditions and material parameters meeting actual conditions were set to carry out finite element simulation for the knitting process. Experiments were done to verify theoretical analysis and effectiveness of finite element simulation result. Through contrastive analysis of finite element simulation result and experimental results, the influence law of friction coefficient, yarn tension and the number of yearn contact points on knitting angle of structural parameter of knit reinforcement was concluded as follows: when friction coefficient of yearns is large, obvious excursion occurs in the knitting process, and the knitting angle of knit reinforcement is less than the theoretical value; when yearn tension increases, the knitting angle of knit reinforcement is closer to the theoretical value; when the quantity of yearns increases in the knitting process, the number of yearn contact points rises, and interaction effect is ehanced so that the knitting angle is less than the theoretical value.

annular knit; yarn interaction; finite element simulation; knit reinforcement

10.3969/j.issn.1673-3851.2017.09.003

2016-12-04 网络出版日期： 2017-03-28

浙江省公益技术研究国际合作项目(2016C34008)

迟进佳(1990-)，男，山东青岛人，硕士研究生，主要从事编织复合材料方面研究。

吴震宇，E-mail：zistwuzhenyu@163.com

TB303

A

1673- 3851 (2017) 05- 0621- 07