基于弧长法对柔性接头高压下屈曲响应研究

黄朝晖，张 潇，刘伟凯

基于弧长法对柔性接头高压下屈曲响应研究

黄朝晖1，张 潇2，刘伟凯1

（1. 中国航天科技集团公司第四研究院，西安，710075；2. 西安航天化学动力厂，西安，710025）

高压下柔性接头摆动力矩减小的原因一直未得到确切解答，只归结到剪应力分布的变化很难让人信服。通过对柔性喷管中柔性接头结构形式的特点进行分析，认为随压强升高摆动力矩减小的根本原因为柔性接头的屈曲响应。分析了弧长法的原理以及其在屈曲分析中的应用，通过数值计算软件ABAQUS开展对柔性接头屈曲过程的仿真分析。分别通过通用静力算法和弧长算法对不同预摆角下承压过程进行模拟，得到摆角随压强的变化规律。计算结果表明：不同压力下的弹性力矩与实验结果对比，一致性较好，所用方法和结论可以为柔性接头高压工作环境下的设计提供有益参考。

固体火箭发动机；弧长法；柔性接头；屈曲；摆动力矩

0 引 言

固体火箭发动机推力向量控制方式有摆动喷管式、燃气舵式和二次喷射式等。摆动喷管的优点在于对发动机的效率影响较小，可实现长时间的方向控制。摆动喷管可分为柔性喷管、珠承喷管和球窝喷管等，其中柔性喷管因为结构简单、工艺成熟而被广泛应用于固体火箭发动机中。柔性接头通过固定体和活动体将柔性喷管与发动机燃烧室连接，并通过自身保持活动体与固定体之间的密封，是固体火箭发动机柔性摆动喷管的核心部件。在柔性接头或柔性喷管的摆动试验和实际工作中存在试验容器或燃烧室工作压强的不断增加，导致柔性接头的弹性力矩减小，从而使得整个喷管的摆动力矩减小，这种现象出现在众多发动机型号中[1,2]。

文献[3]～[10]对柔性接头的生产设计、高压或者不同温度工作时的力学响应、结构的可靠性、强度及稳定性进行了分析，为固体火箭发动机柔性接头的设计提供了参考，但是对于高压下柔性接头摆动力矩减小的根本原因分析较少；王雪坤等[11]开展了弹性件材料的双轴向加载拉伸试验，设计了代表柔性接头中弹性件结构特性的三重片、四重片橡胶试件，对试件压缩的同时进行剪切联合加载试验，开展了有限元数值仿真计算，得到橡胶材料本身的剪切模量随外界压强的变化规律；王春光等[12]分析了随压强的增大柔性喷管弹性力矩减小的原因，利用ABAQUS有限元数值模型模拟了柔性接头的摆动过程，计算得到弹性件上的切应力分布，认为切应力分布随容器内压强变化是弹性力矩减小的内在原因。

本文分析认为，弹性件上的剪切应力分布随容器内压强变化并不是柔性接头摆动力矩减小的根本原因，而是柔性接头在燃烧室内压及力矩的双重作用下，整体机构对外力产生一种响应，该响应导致弹性件任意剖面上的剪切应力分布发生变化，最终导致弹性力矩减小。柔性接头在高压及摆动联合作用下的屈曲现象是：首先以响应为前提，然后有剪切应力分布变化，最终导致弹性力矩变化。

屈曲分析多用来研究和分析结构在特定外界载荷下的稳定性或者确定结构在失稳时刻的临界载荷，主要分为非线性屈曲分析和线弹性屈曲分析。线弹性屈曲分析又称为特征值屈曲分析，非线性屈曲分析主要包括：弹塑性失稳分析、几何非线性失稳分析和非线性后屈曲分析等[13]。弧长法有效地分析了结构非线性前、后屈曲，而且对屈曲路径进行跟踪，在非线性屈曲分析中应用较多[14,15]。

本文根据屈曲分类，通过ABAQUS计算软件中的通用静力非线性计算分析和弧长法计算分析对柔性接头的摆动过程进行数值计算，将计算结果与试验所得结果进行对比，分析了柔性接头结构在高压及摆动作用下的屈曲响应特性。

1 柔性接头的屈曲响应及计算方法

型号研制中，柔性接头每件产品都要在地面进行冷态性能摆动试验，测试时必须模拟不同的燃烧室压强。柔性接头摆动试验过程如图1所示。由图1可知，接头安装在容器上，容器内压强可变，用刚性摆杆代表喷管扩张段，B、C两点之间安装作动器，施加摆动力矩。

1.1 柔性接头工作过程及结构特性

柔性接头是由多个同一中心的环状球面增强件和弹性件一层覆盖一层粘接在一起，在最外侧和最内侧都有一个法兰组成的一个整体，弹性件材料主要是天然橡胶或硅橡胶，增强件材料是金属或碳纤维复合材料，柔性接头结构如图2所示。

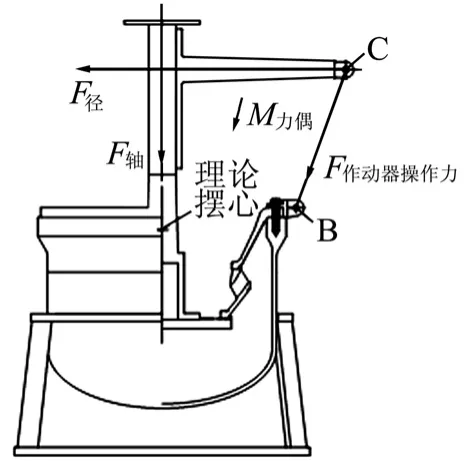
图1 柔性接头的 摆动试验示意

柔性接头为非线性橡胶堆结构，其摆动过程见图1，作动器收缩施加摆动力矩，作动器的操纵力通过摆杆（实际发动机中为喷管结构）传递到柔性接头前法兰，实现柔性接头摆动。在内压载荷作用下，柔性接头同时受到摆动载荷的双重加载。实验发现，柔性接头在受侧向压缩时，弹性力矩减小，从而造成摆动力矩的减小。

图2 柔性接头结构形式

研究结构的屈曲临界载荷或屈曲后特性的方法有非线性屈曲分析和特征值（线性）屈曲分析两种。特征值屈曲分析通常属于结构的线性去屈曲分析，用于研究理想的线弹性结构自身的理论屈曲载荷（即分叉点）。由于柔性接头的特殊结构形式，且橡胶为超弹性材料；另外由于压力和摆动的双重作用，接头的屈曲过程应为非线性屈曲过程。非线性屈曲分析一般考虑结构有一定初始缺陷，如长度的千分之一、壁厚的十分之一、按实际生产中的制造误差赋值和外力的初始扰动等。

分析认为，对于柔性接头结构的屈曲过程与橡胶堆结构类似[16]：接头摆动力矩相当于侧向力的初始扰动，使接头产生一定转角位移，在压力的作用下，随压力升高，相同的力矩可以产生更大的转角位移。特别说明的是，侧向摆动力矩与压力载荷是分别加载的，通过前期仿真及试验验证，二者的加载次序并不影响弹性力矩的减小效果。以上过程即为柔性接头的失稳过程。

1.2 弧长法理论计算过程

弧长法属于双重目标控制方法，即在求解过程中同时控制荷载因子和位移增量的步长。弧长法的迭代求解过程如图3所示。

图3 弧长法迭代示意

从图3中可以发现，若荷载增量Δλij=0(j ≥2)（其中，下标i为第i个荷载步，上标j为第i个荷载步下的第j次迭代），则迭代路径变为平行于x轴的一直线段，这就是著名的Newton-Raphson方法。

设第i−1个荷载步收敛于（xi−1,λi−1），则对于第i个荷载步，需要迭代j次才能到达新的收敛点（xi,λ）i上。在ABAQUS算法中，外部参照载荷{Fref}需要用户以外荷载的形式进行输入。因此，作用在所研究结构上的真实外力为λ{Fref}。由于Newton-Raphson方法在迭代过程中，以位移控制（或荷载控制）时，位移增量步长Δλ（或荷载增量步长）为常数，无法越过极值点而得到完整的荷载-位移曲线。实际情况中，要想使求解过程越过极值点，只有不断变化荷载的增量步长。

由图3还可以发现，弧长法的荷载增量步长Δλ是在不断变化的，可以自动进行荷载控制，但这个过程又使得原来的方程组增多了一个多余的未知变量，因此要想求解还需要补充一个控制方程，即：

由式（1）可以发现，其迭代路径实际上是以上一个荷载步的收敛点（xi−1,λi−1）为圆心，半径为li的圆弧，因此称为弧长法。一般情况下，要求用户指定初始弧长半径l1或固定的弧长半径l0，一旦设定了初始弧长半径，依据收敛速率的快慢，可按式（2）计算il：

式中 nd为荷载步希望收敛迭代的次数，通常取为6；ni−1为前一荷载步的迭代次数，如果大于10时就取10。

若在计算中考虑材料塑性的影响，则每个迭代step的切线刚度矩阵需要以当前迭代步的构形为依据，因此切线不再平行。

2 数值计算模型及计算过程

柔性接头计算模型如图4所示[2]。

图4 柔性接头计算模型

续图4

由图4a可知，对前法兰及堵盖整体施加压强载荷可实现不同试验容器内压强的模拟，驱动载荷通过在虚拟摆心施加力矩实现，虚拟摆心通过刚性杆与前法兰相连。橡胶材料使用超弹本构模型模拟，增强件为钢材料。

有限元模型单元总数约为20 000个，其中橡胶弹性件设置9层，金属增强件设置8层，整个接头沿周向平均划分为35等份，在接头的宽度方向划分为20等份，弹性件在厚度方向划分为5层，增强件划分为3层。弹性件橡胶材料全部采用杂交单元C3D8H模拟，增强件采用减缩积分单元C3D8R模拟；前后法兰、加压盖板以及加载部分近似看成刚性体，使用刚体单元R3D4模拟[2]。

计算工况可分为两步：a）将柔性接头沿摆心预摆一定角度，相当于初始扰动或结构的初始缺陷；b）对接头分别施加压力载荷，最大为6 MPa（发动机实际燃烧室最大压强），可用通用静力非线性计算分析和弧长法计算分析进行计算。

预处理单元是将大颗粒的污染物及指标处理至要求限值，同时去掉或分解掉对主体单元处理效果有较大影响的的污染物。本工艺的预处理主要包括分质预处理和综合预处理。分质预处理包括爆珠隔油预处理系统和油墨清洗废水脱色预处理系统，综合预处理为格栅、调节池。

3 仿真结果与试验对比分析

仿真计算分别通过通用静力非线性计算分析和弧长法计算分析进行计算，计算结果如图5所示。

图5 计算变形

续图5

初始接头摆动为1°，随压力的增加，摆动角逐渐增大，同时弹性力矩减小，摆角最大增大到2.435°，如图5a所示。随着压力的增加橡胶弹性件的网格变形严重，当压力接近6 MPa时，网格畸变，计算被迫中止，局部网格变形如图5b所示。

预摆角设为0.5°、1°、2°和3°，最大压力设为6 MPa，计算不同压力下的摆角变化形式，如图6所示。

图6 压力摆角变化曲线

从图6中可以看出，非线性法与弧长法计算结果接近，但用非线性法计算的压力略高于弧长法。

在非线性屈曲分析中，通过观测载荷-位移曲线来判断结构的失稳点及失稳过程。结构的载荷位移曲线主要有以下3种形式，如图7所示。根据载荷位移路径的变化，屈曲又分为极限屈曲、稳定分支屈曲和不稳定分支屈曲。

图7 不同情况下的载荷位移曲线

对比图7中3种图形，柔性接头的屈曲过程更接近图7b的稳定分支屈曲过程，但是柔性接头无确定的临界载荷。分析认为，由于柔性接头特殊的非线性结构，随压力的增加，结构摆角增大，说明结构形状时刻在发生变化，对于用静力结构分析这种变形都属于大变形范畴，后一步的变形形式直接由前一步的变形所决定，因此新结构形式的临界载荷也应该时刻变化。

另外，随着预摆角的增加，不同曲线的斜率变化越加明显，说明结构的失稳越严重。由于预摆角增大时，侧向扰动增大、相同压力下摆角增加量更大、结构更倾向于严重失稳。

计算非线性和弧长法在不同压力下的弹性力矩，将所得数据与实验结果对比，弹性力矩变化趋势如图8所示。

图8 弹性力矩随压力变化趋势示意

由图8可知，非线性和弧长法计算所得弹性力矩变化趋势基本相同，只有微小变化。计算结果表明，数值计算与实验所得到的结果基本一致，误差变化范围较小，但是实验结果的弹性力矩下降趋势比数值计算结果更为明显。分析认为，误差产生的原因是有限元建模时并未考虑到柔性接头实际生产中的制造偏差，如弹性件、增强件的厚度不均匀等，实际生产中的尺寸误差可能成为初始扰动的一部分，从而导致接头更容易发生偏转，即弹性力矩下降更快；在较高的容器压强下，橡胶单元处于大变形状态，计算结果偏离真实值，数值模型很难全程捕捉实际模型的各种力学行为。

为了说明预摆缺陷与制造缺陷对接头屈曲失稳状态影响的差别，分别将预摆角1°、3°和制造偏差产生的1°、3°的模型进行屈曲仿真分析，施加最大压力6 MPa，计算不同压力下的预摆角变化，计算所获得结果如图9所示。由图9可知，预摆缺陷与制造偏差缺陷对接头屈曲的影响趋势相同，制造偏差产生的失稳形式更为严重。该结论证明了侧向力与摆角制造偏差都是使接头产生高压失稳的原因之一。

图9 预摆角与制造偏差对摆角的影响

4 结 论

对柔性接头的屈曲特性进行分析，通过不同计算方法对柔性接头预摆条件下的承压进行模拟，并对比实验结果，得到如下结论：

a）柔性接头高压下弹性力矩减小的根本原因为：柔性接头在外部摆动力矩和燃烧室压强共同加载作用下的屈曲响应，接头摆动力矩相当于侧向力的初始扰动，使接头产生一定转角位移；在压力作用下，随压力升高，相同力矩会产生更大的摆角位移，即弹性力矩减小。

b）非线性方法和弧长方法均可以较好地模拟接头的摆动失稳过程，且非线性方法跟踪的路径范围更大，可以计算得到较高压强下的结果，说明弧长方法并不是在所有情况下都优于非线性方法。通过非线性方法与弧长方法的模拟，发现柔性接头的屈曲过程为稳定分支屈曲过程，但是数值仿真方法仍无法捕捉到柔性接头确切的屈曲临界载荷。

c）非线性方法和弧长方法计算得到弹性力矩变化趋势基本相同，只有微小变化。对比实验所得结果，数值仿真计算所得到的结果与实验获得的结果趋势基本一致，误差在较小范围内，说明两种方法均可以用力模拟柔性接头的屈曲行为，用来进行柔性接头的前期优化设计。

d）通过对比制造偏差（如弹性件厚度不均匀）与预摆角对接头屈曲的影响，可以发现两种情况下接头的屈曲失稳形式一致，该分析可以较好地解释在实际加压实验中，柔性接头自己倾倒的现象。

[1] 陈汝训, 刘铭初, 李志明, 等. 固体火箭发动机设计与研究[M]. 北京:中国宇航出版社, 2007.

[2] 王春光, 史宏斌, 王雪坤, 等. 高压下喷管柔性接头摆动力矩数值分析[J]. 推进技术, 2011, 32(2): 202-206.

[3] 张晓光, 刘宇, 任军学, 等. 小型柔性接头推力矢量性能试验[J]. 航空动力学报, 2012, 27(12): 2836-2840.

[4] 王超, 任军学, 郝文强, 等. 柔性接头有效摆心漂移特性[J]. 航空动力学报, 2014, 29(12): 2993-2996.

[5] 史宏斌, 等. 控制力作用柔性喷管动力响应研究[J]. 航空动力学报, 2003, 18(4): 563-568.

[6] Shani S, Putter S, Peretz A. Development of a high-performance flexible for thrust vector control[R]. AΙAA95-3047, 1995.

[7] Donat J R. Solid rocket motor nozzle flexseal design sensitivity[R]. AΙAA93-1122, 1993.

[8] 安春利, 常新龙. 柔性接头弹性件超弹性本构参数拟合和低压摆动非线性有限元分析[J]. 固体火箭技术, 2008, 31(1):79-85.

[9] 曹翠微, 陈伟民. 固体火箭发动机柔性接头的结构分析[J]. 推进技术，2006, 27(5):450-454.

[10] 曹翠微, 陈伟民, 蔡体敏. 固体火箭发动机柔性接头弹性件力学性能研究[J]. 宇航材料与工艺, 2005, 35(5): 36-41.

[11] 王雪坤, 王春光, 史宏斌. 柔性接头弹性件压缩剪切联合加载试验研究及数值分析[J]. 固体火箭技术, 2011, (34)3: 364-368.

[12] 王春光, 田维平, 史宏斌, 等. 弹性件剪切模量随压力变化的试验分析[J]. 宇航材料工艺, 2011, 41(5): 81-86.

[13] 韩强. 弹塑性系统的动力屈曲和分叉[M]. 北京: 科学出版社, 2000.

[14] Alfano G, Crisfield M A. Solution strategies for the delamination analysis based on a combination of local control arc-length and line searches[C]. Sydney: Ιnternational of Journal Numerical Methods in Engineering, 2003.

[15] Souza D E， Neto E A， Feng Y T. On the determination of the path direction for arc-length methods in the presence of bifurcations and snapbacks[J]. Computer Methods in Applied Mechanics and Engineering, 1990, 179(1-2):81-89.

[16] 刘文光. 橡胶隔震支座力学性能及隔震结构地震反应分析研究[D]. 北京: 北京工业大学, 2003.

Research on the Buckling Response of the Flexible Joint Based on Risks Method

Huang Chao-hui1, Zhang Xiao2, Liu Wei-kai1
(1. The Fourth Academy of CASC, Xi′an, 710025; 2. Academy of Aerospace Solid Propulsion Technology, Xi′an, 710025)

The mechanism of the deflection torque of the flexible joint decrease with enhancing pressure has never been resolved. Just say the shear stress has changed can not be convincing. The structure of the flexible joint are analyzed, the real reason for the deflection torque of the flexible joint decrease is that it would be buckling when it bearing the deflection and pressure at the same time. The risks method is analyzed and used in this paper, the buckling process of the flexible joint is simulated by ABAQUS. The risks method and static general method are used to simulate the different processes of different pre-angle with enhancing pressure, the rules of pendulum angle changing with the enhancing pressure are got. The spring torque is got and had a good coherence with the test results. The method and conclusion in this paper will provide the beneficial reference for the design of the flexible joint in high-pressure work environment.

Solid rocket motor; Risks method; Flexible joint; Buckling response; Deflection torque

V435

A

1004-7182(2017)04-0102-06

DOΙ：10.7654/j.issn.1004-7182.20170423

2017-05-25；

2017-06-06

黄朝晖（1968-），女，高级工程师，主要研究方向为固体火箭发动机结构与强度研究