基于单个磁梯度计的磁目标定位方法研究

贾文抖， 林春生， 孙玉绘， 翟国君

(1.海军工程大学 兵器工程系， 湖北 武汉 430033； 2.海军工程大学 导航工程系， 湖北 武汉 430033；3.海军海洋测绘研究所， 天津 300061)

基于单个磁梯度计的磁目标定位方法研究

贾文抖1， 林春生1， 孙玉绘1， 翟国君2,3

(1.海军工程大学 兵器工程系， 湖北 武汉 430033； 2.海军工程大学 导航工程系， 湖北 武汉 430033；3.海军海洋测绘研究所， 天津 300061)

欧拉法可以实现对磁偶极子源的精确定位。通过旋转合成可以得到包含在欧拉齐次方程中的磁梯度张量，在此基础上提出了一种转动单个矢量磁梯度计实现磁目标定位的方法。建立了磁梯度计旋转探测模型，分析了模型中转动角、倾角和基线长度等参数对磁目标定位精度的影响，为转动装置的参数设置提供了参考。研究结果表明，与7个磁传感器组成的阵列探测方法相比，该旋转探测方法在靠近磁目标的区域内具有更高的定位精度。

电磁学； 磁张量； 欧拉法； 磁梯度计

0 引言

磁张量能够有效地弱化背景磁场的干扰[1-2]，突出局部磁异常的存在，联合目标磁场分量(Bx,By,Bz)，利用欧拉法可以实现对磁源目标的精确定位。磁张量具有定位精度高、速度快、便于实时处理等优点，在军民两用领域都具有广阔的应用前景。

当前基于磁张量信息的定位方法中，多是以差分替代微分的方式来获取磁张量数据。为获得磁张量中的9个元素量及目标磁场分量(Bx,By,Bz)，将7个矢量磁传感器[3]布置在3个相互垂直的棒杆两端，形成空间立体测量结构，这是最直接的测量定位方式，后来出现了一些简化测量方法。例如，张朝阳等[4]将上述空间立体测量结构简化成5个磁传感器组成的平面测量结构，并对其探测定位效果进行了分析。张光等[5]利用将同样的测量结构搭载在运动载体上，利用两个位置上测量数据的差值有效消除了背景磁场的干扰。庞洪锋等[6]研究了采用4个磁传感器的目标定位方法；于振涛等[7]进一步提出利用3个矢量磁力仪等腰直角布置的方式，可实现对水中的磁性目标的监测定位，但由于磁力仪的数目较少导致定位精度有所下降。

考虑到差分替代微分会有一定的计算误差，且测量装置的磁传感器数目较多时安装复杂，若使磁传感器间三轴指向一致，匹配难度大，而磁传感器数目较少时定位精度又会有所下降，为了降低差分计算磁张量数据时的误差，同时减少磁传感器之间的匹配难度，提出了一种基于单个矢量磁梯度计的旋转探测定位方法，通过磁梯度计的转动来捕获空间冗余的磁场信息用于计算磁张量，以实现磁源目标的定位。

1 磁目标的定位原理

欧拉反褶积方法[8]是一种自动估算场源位置的位场反演方法，建立在欧拉齐次方程基础之上，它联系了位场和其梯度与场源之间的关系，通过欧拉齐次方程组的求解，可以确定场源的空间位置。由等效磁偶极子近似模型可知，在距离超过磁性物体自身尺寸2.5倍以上的距离处，磁性物体的磁场分布近似于一个磁偶极子的磁场分布[9]，因此，在适当远的距离上可以通过偶极子的定位来实现对磁目标体的定位。

基于欧拉方程的磁偶极子定位方程为

(1)

式中：(Bx,By,Bz)是源点在空间(x,y,z)处产生的磁场三分量；(x0,y0,z0)为磁源的位置坐标，场点坐标为(x,y,z). 为了计算简便，以源点为坐标原点，(1)式可整理为

(2)

以G表示磁张量矩阵，B表示磁场分量，X表示场点坐标。可将(2)式简化为

GX=-3B.

(3)

进一步变形为

X=-3BG-1.

(4)

(4)式是磁偶极子的定位方程。

2 磁张量的计算

磁场是一个矢量场，其三分量在空间3个方向的导数构成了磁张量的9个分量。其表达式为

(5)

为了获得张量全要素，设计了如下的测量方法。

如图1所示，两个三轴磁力仪固定在无磁探杆两端，磁力仪a、磁力仪b对应的三轴指向一致，且磁力仪的y输出轴水平，在竖直方向将探杆固定，使探杆轴线与重垂线的夹角为θ，坐标系原点位于探杆的中点O处，探杆在Oxy面上的投影与x轴的夹角为φ，a、b间探杆基线长度为l.

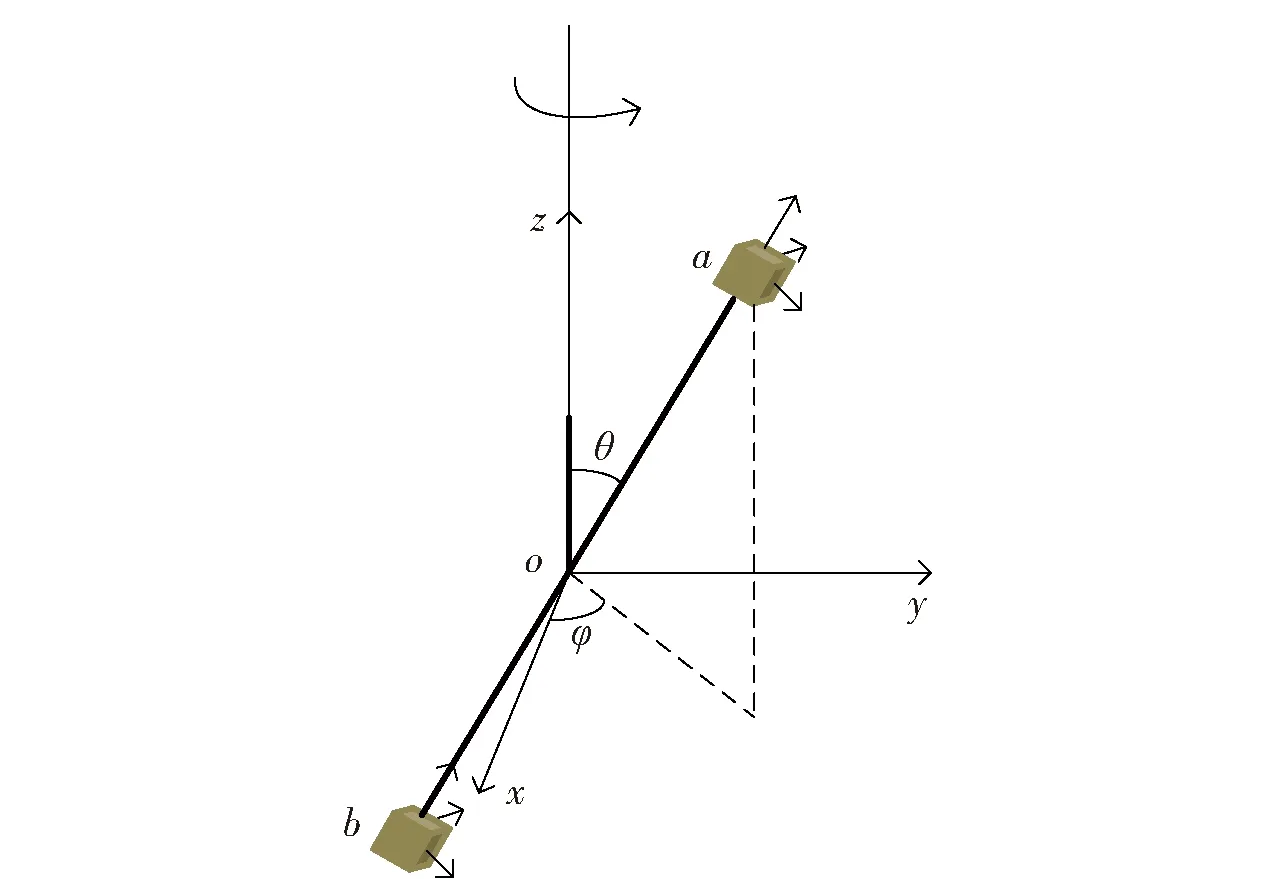
图1 磁梯度计转动示意图Fig.1 Schematic diagram of rotation of magnetic gradiometer

由于磁力仪自身的3个输出轴与坐标系三轴指向不一致，首先将矢量磁强计的实际输出转换成与坐标系三轴指向一致的3个分量。以图1中磁梯度计所在位置为例，矢量磁力仪a的三轴输出为Ba=[Bax,Bay,Baz]T，欲使磁力仪自身坐标系三轴指向与坐标系x、y、z三轴指向一致，首先将磁力仪a自身坐标系绕自身的ya轴顺时针(从ya轴正方向看负方向)转过θ角度，旋转矩阵为Ry(θ)，然后在绕za轴顺时针(从za轴正方向看负方向)转过φ角度，旋转矩阵为Rz(φ)，转动后二者指向一致。根据欧拉旋转公式可得坐标系中对应的磁场量为

B=Rz(φ)Ry(θ)Ba,

(6)

即

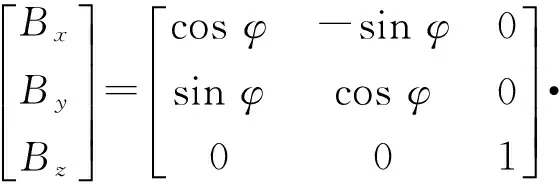
(7)

在得到坐标系三轴指向下的测量值后，利用磁梯度计的输出进行磁张量数据的计算。在磁场空间中，磁梯度计两端有

ΔB=[ΔBx,ΔBy,ΔBz]T=
[Bax-Bbx,Bay-Bby,Baz-Bbz]T.

(8)

根据全微分的概念，有

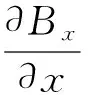
(9)

磁梯度计绕重垂线(坐标系中z轴)转动时，根据(9)式，对应于不同的转动角φ1、φ2、…、φn可得方程组：

(10)

解方程组(10)式可以得到Gxx、Gxy和Gxz；类似地，利用ΔBy和ΔBz的全微分表达式和转动角φ1、φ2、…、φn对应的磁测数据，可计算得到Gyx、Gyy、Gxz、Gzx、Gzy和Gzz，即可实现磁张量的计算。

3 参数的设定

根据(10)式可知，图1模型中的待定参数有旋转角φ、基线l和倾角θ. 从一般意义上讲，确定这3个参数属于多参量的优化问题，常规的优化方法存在较大的盲目性，计算量大，从数学上计算得到优化结果后，还需要从工程角度考虑是否可行，并进行相应调整，整个优化过程较为繁琐。为此，在工程应用可行方案的基础上，采用一种非常规的分步优化方法，以应用效果最大化为目的出发，直接针对可行方案有针对性地进行分步优化来确定模型参数，可有效地排除掉大部分不可行的参数解，避免了常规优化方法计算的盲目性。

参数的优化选取依据理想模型的定位误差最小为原则确定。以磁目标为坐标原点，目标的磁矩M=(3 200 A·m2,470 A·m2,-1 200 A·m2)，以探杆的中点为测量场点(x,y,z)的位置，相对磁源的坐标为(8 m,-14 m,3 m)。

3.1 旋转角φ的设定

从(10)式中可以看出，方程组中只有3个未知数，因此，最少需要3个不同φ角对应的磁场测量值即可实现张量数据的求解。在初始设定倾角θ=30°、基线长度l=1 m时，取φ的3个转动角为10°、25°和40°，得到的空间反演结果见表1.

表1 测点位置的反演结果

从表1中的反演数据可知，在测点相对于磁源目标的空间坐标为(8 m,-14 m,3 m)时，此时二者之间的直线距离约为16 m，定位误差仅为0.02 m.

在实际中φ角易发生小幅度的左右晃动或出现一定的测量误差，在此可一并考虑。假定φ角在预设定值附近发生轻微的晃动，晃动角在2°以内，随机进行150次试验，定位误差曲线如图2所示。

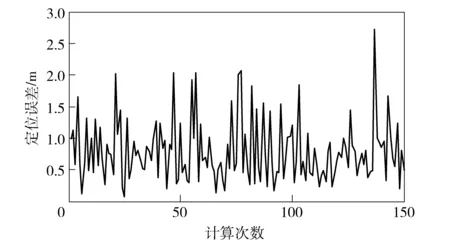
图2 150次随机试验的定位误差曲线图Fig.2 Positioning error curve of 150 randomized trials

从图2可以看出，φ的晃动角幅度不超过2°时，150次随机试验中有一部分定位误差大于1 m，少数达到甚至超过了2 m，定位偏差较大。下面分析如何对转动角φ取值来降低晃动角对定位结果的影响。

3.1.1 加密φ角取值点

保持φ角在10°～40°的范围内取值，φ角取样间隔减小为5°，此时可取7组磁场测量值，进行150次随机试验后定位误差曲线如图3所示。

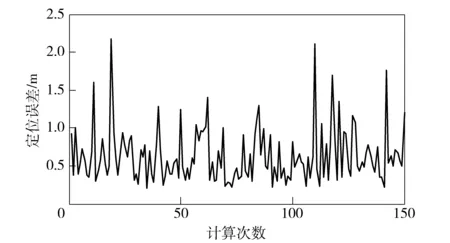
图3 150次随机试验的定位误差曲线图Fig.3 Positioning error curve of 150 randomized trials

从图3中的定位误差曲线可以看出，在保持φ角在较小的转动角范围内取值时，仅依靠增加磁场值的测量数量，并不能明显改善定位效果。

3.1.2 增大φ角转动幅度

保持最少的磁场值测量数量，加大φ角的转动取值范围，使梯度计在360°转动空间中测量磁场，φ角依次取值为120°、240°和360°，此时φ角的晃动幅度仍保持在2°以内，随机进行150次试验，定位误差曲线如图4所示。

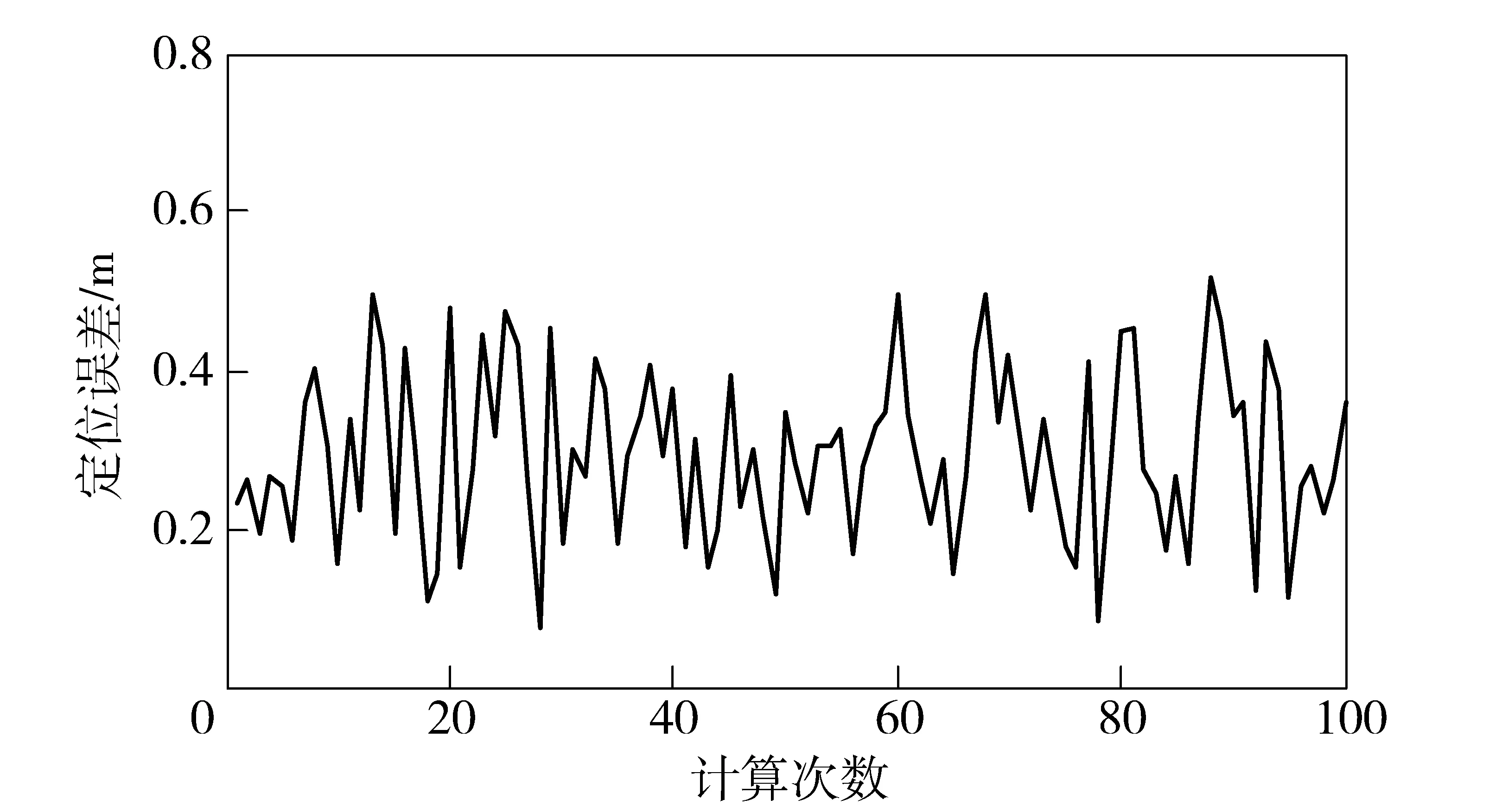
图4 150次随机试验的定位误差曲线图Fig.4 Positioning error curve of 150 randomized trials

在扩大φ角的转动取值范围后，150次随机试验的定位误差都不超过0.6 m，与图3中的结果相比，增大φ角转动幅度，可以明显改善定位结果，降低定位误差，提高定位的稳定性。

3.2 基线l的设定

在设定转动角φ分别为120°、240°和360°，对如何设定探杆基线l进行分析。在0.1～3.0 m的长度范围内，定位误差随基线l的变化关系如图5所示，从中可以看出，基线l较短时的定位准确性较高，随着探杆长度的增加，定位误差明显增加。

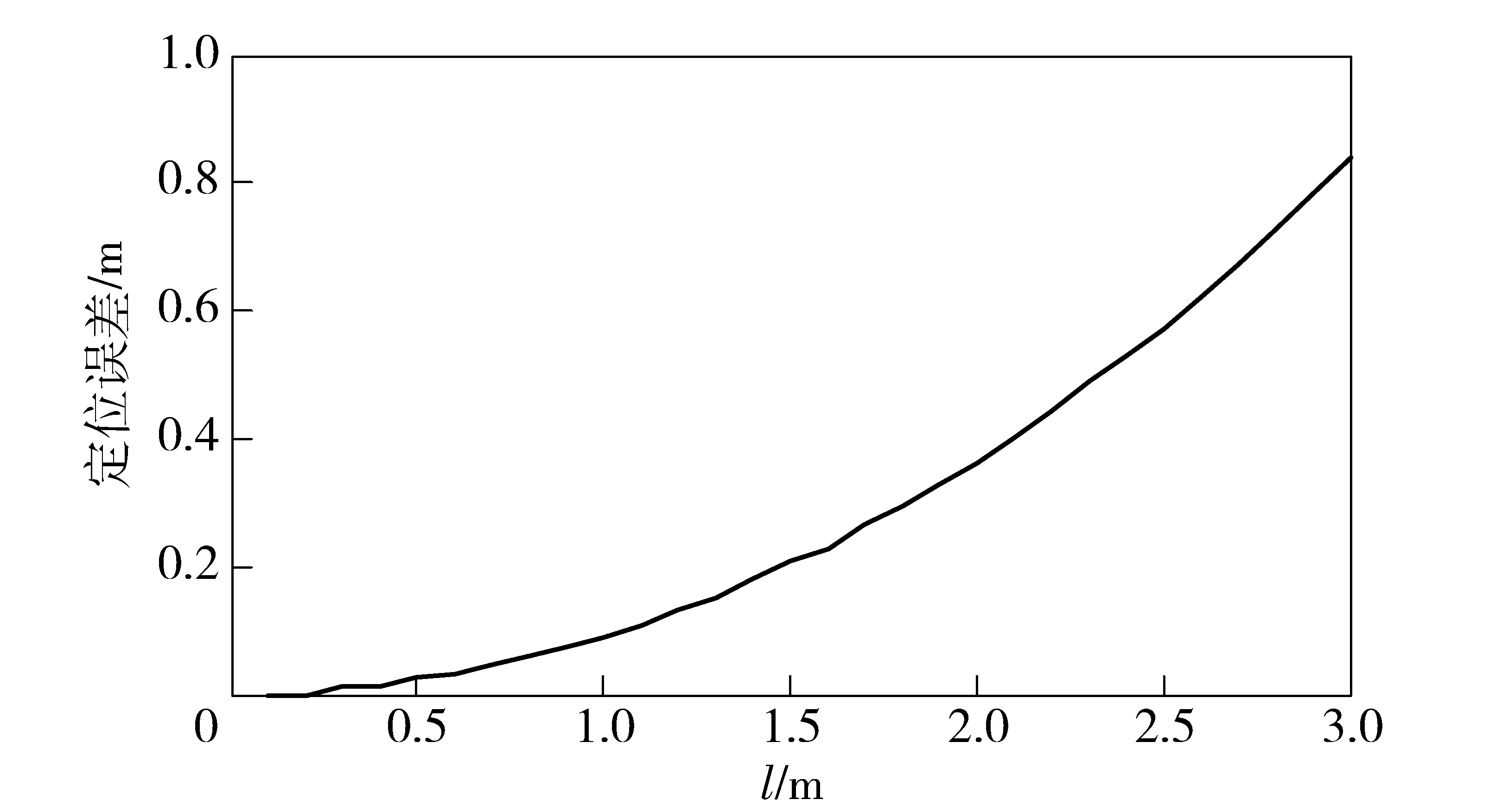
图5 定位误差与基线l的关系曲线图Fig.5 Relation between positioning error and baseline l

3.2.1φ角晃动

当转动角φ出现2°以内的晃动时，定位误差随基线l的变化关系如图6所示。由图6可以看出，在转动角φ发生一定的晃动时，定位误差同样随着基线l的增加而变大，在不超过1.5 m时，定位误差曲线变化较为平缓。

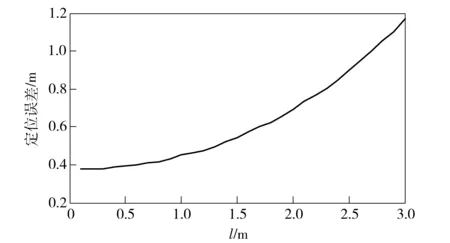
图6 φ角晃动不超过2°时定位误差曲线图Fig.6 Positioning error curve for φ ≤ 2°

3.2.2 随机测量噪声

当磁场测量值中含有2nT左右的测量噪声时，从图7中定位误差随杆长的变化关系曲线可以看出，杆长小于0.5 m和大于2.5 m时，误差较大，在0.5～2.5 m，尤其是1.0～1.5 m时，定位误差较小。

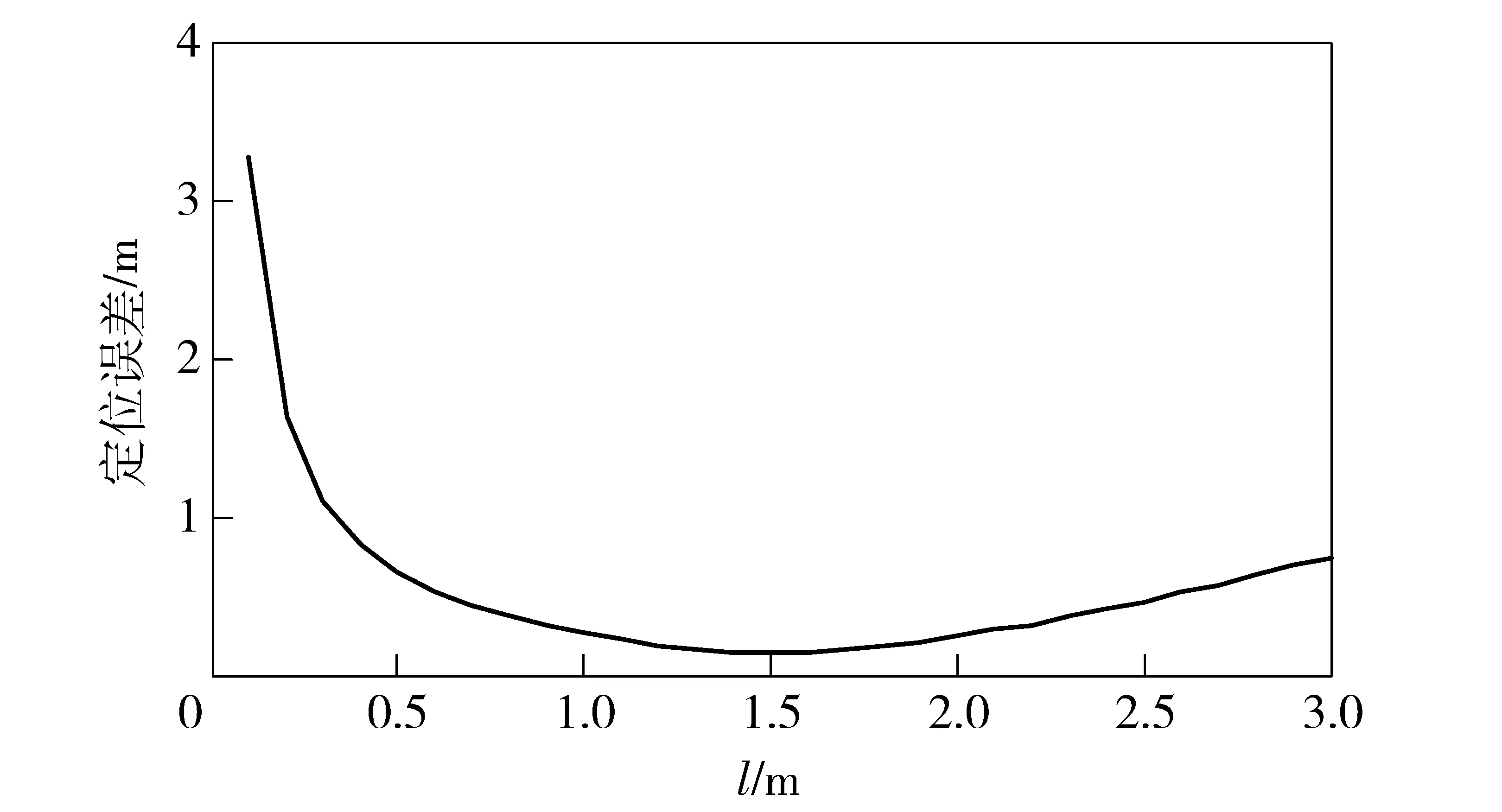
图7 磁测数据中含有2nT噪声时定位误差曲线图Fig.7 Positioning error curve in the case of 2nT noise existing in magnetic field measurement data

考虑到两个磁力仪测得的磁场值应具有一定的差异，二者之间的距离不宜过近，同时梯度测量装置的尺寸也不能过大，因此取基线l=1.0 m是比较合适的。

3.3 倾角θ角的设定

在取定一组较佳的φ角为120°、240°和360°及基线l=1 m后，下面分析如何对磁梯度计的安装倾斜角θ进行设定。理论上θ角的取值范围为0°～90°，当θ角取到0°或90°后，倾斜杆退化成竖直或水平，失去了本文研究的意义，故将其取值范围设置为1°～89°，定位误差随倾角θ变化的曲线见图8.

图8 定位误差与倾角θ角的关系曲线图Fig.8 Positioning error vs. inclination angle

从图8中可以看到，在1°～89°的范围内，随着θ角的增加，定位误差呈现增大的趋势变化，在θ角不超过80°时，定位误差变化不明显，基本不超过0.1 m.

3.3.1φ角晃动

若φ角出现一定幅度的晃动，取转动角φ的晃动幅度不超过2°，计算得到的定位误差随倾角θ变化的关系曲线如图9所示。

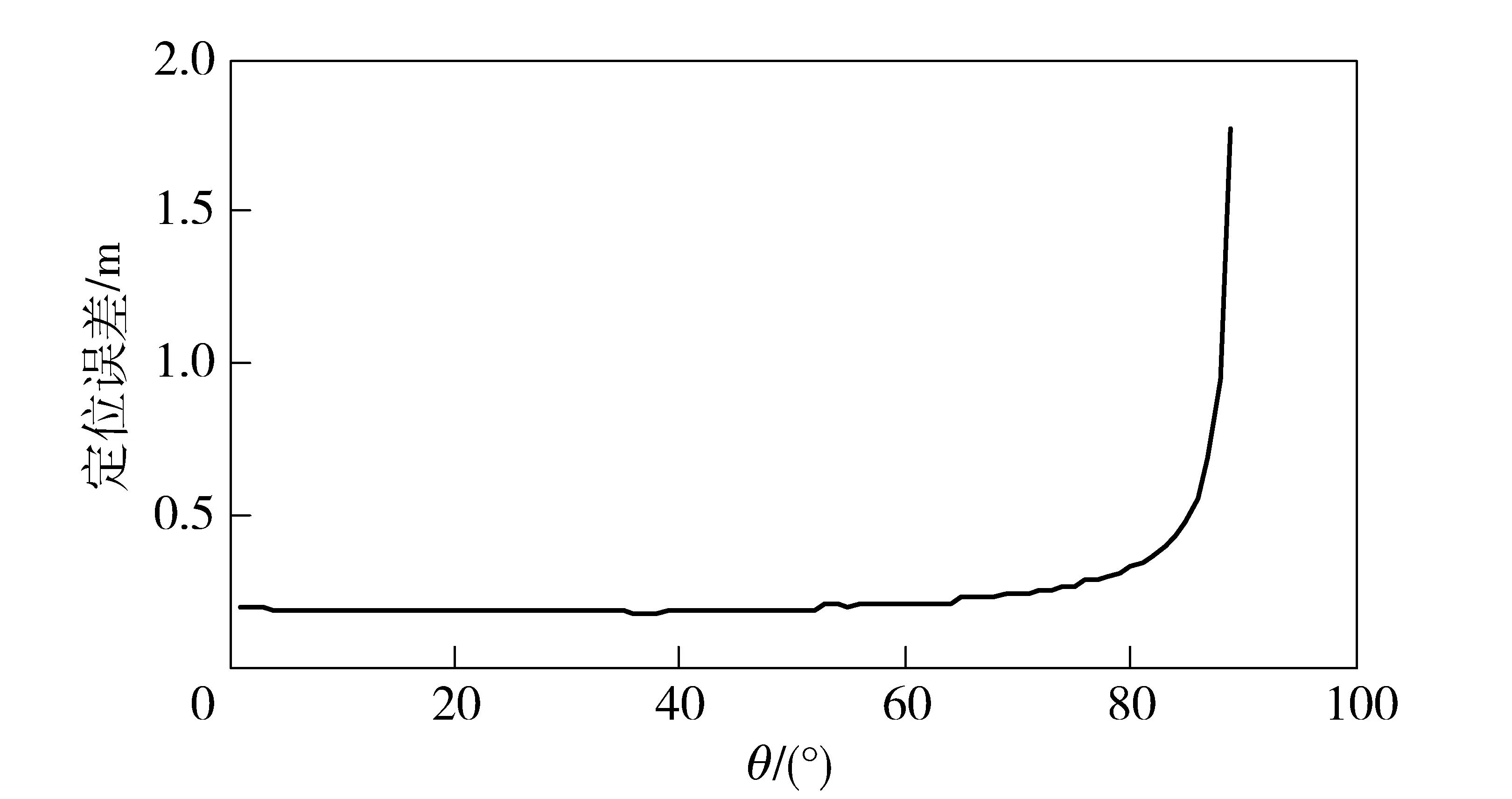
图9 φ晃动角不超过2°时定位误差曲线图Fig.9 Positioning error curve for φ≤ 2°

从图9与图8的比较可看出，在φ角出现晃动时，定位误差较原来相比有所增加，同样随θ角的增加而增加，当θ角不超过80°，定位误差小于0.4 m.

3.3.2 随机测量噪声

在设定随机测量噪声水平为2nT后，为了更加明显地观测到定位误差随θ角的变化趋势，将目标磁矩增大到原来的10倍，随机进行两次试验结果如图10所示(为了更加明显的展示中间部分的曲线变化细节，定位误差超过2.0 m的点不在图10中进行展示)，从中可以看出定位误差随θ角的增大先减小后增加，两端的定位误差明显大于中间部分很多，多次试验发现相较于其他θ角取值范围，θ角在40°～80°内取值，定位误差都是比较小的。

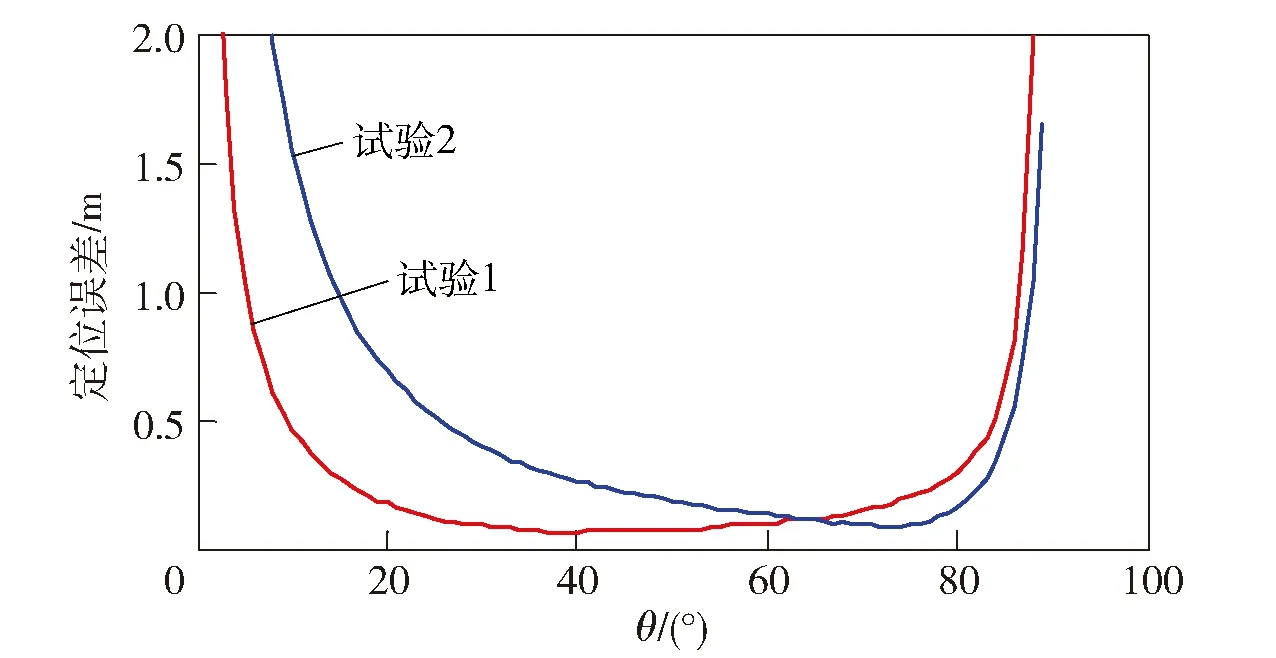
图10 磁测数据中含有2nT噪声时定位误差曲线图Fig.10 Positioning error curve in the case of 2nT noise existing in magnetic field measurement data

综合比较图8～图10所示的定位误差曲线，为了尽量降低定位误差的同时保证定位的稳定性，可将倾角θ设定为60°.

4 与7个磁传感器阵列进行比较

设定基线l=1.0 m，转动角φ分别为120°、240°和360°以及倾角θ=60°，目标磁矩设M=(0 A·m2,0 A·m2,4 000 A·m2)，将本文所用的探测系统模型与上文中所提到的7个磁传感器阵列系统的定位结果进行比较，在以磁源为中心点，在z=3 m，边长为40 m的方形区域中间隔1 m取测点，共进行1 681次定位，结果如图11和图12所示。

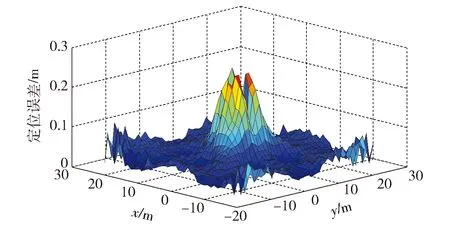
图11 本文所用方法的定位误差Fig.11 Positioning error of the method in the present paper

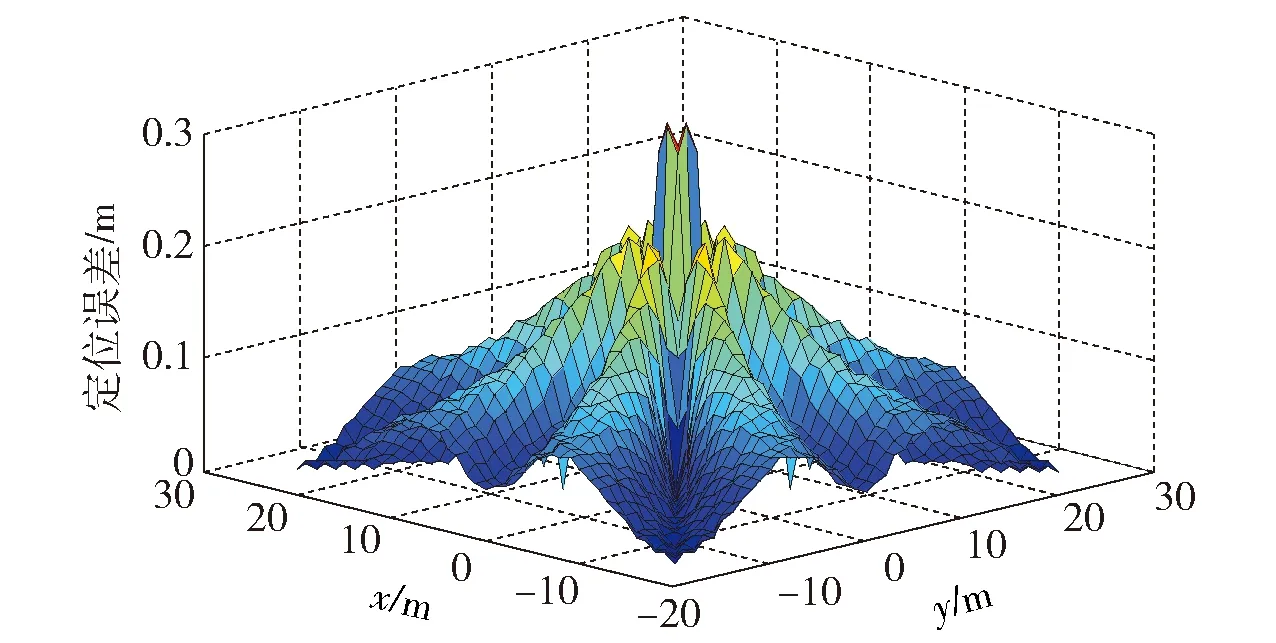
图12 7个传感器组成阵列的定位误差Fig.12 Positioning errors of the array with 7 sensors

通过误差图及实际计算数据的比较可知，在所研究空间的绝大部分区域中，本文所提的方法定位精度优于由7个传感器组成阵列探测方法，这个较优的区域大致可圈定在以磁源为中心、半径为r(r不超过20 m)的圆形范围内，超过此空间范围后，本文方法存在随距离增加定位误差逐步加大的缺陷。

5 结论

本文提出了一种基于单个矢量磁梯度计的旋转探测方法，有效获取了目标的磁梯度张量信息，实现了对磁目标的精确定位。通过比较选取了一组较优的参数：旋转角φ取120°、240°、360°，倾角θ=60°，基线l=1 m. 与7个磁传感器组成的阵列探测方法相比，在距离磁目标不超过20 m的范围内，该探测方法具有更高的定位精度。

由于本文采用的是在空间上旋转的顺序测量方法，不同旋转角对应磁场数据必然有时间上的延迟，因此该探测方式适用于对实时性要求不高的场合。为满足实时性要求，可将多个磁梯度计倾斜交叉布置。

References)

[1] 吕俊伟，迟铖，于振涛，等．磁梯度张量不变量的椭圆误差消除方法研究[J]．物理学报，2015，64(19)：52-59． LYU Jun-wei, CHI Cheng, YU Zhen-tao, et al. Research on the asphericity error elimination of the invariant of magnetic gradient tensor[J]. Acta Physica Sinica, 2015, 64(19): 52-59. (in Chinese)

[2] 陈谨飞，张琦，潘孟春，等．基于正六面体结构测量阵列的磁异常定位技术研究[J]．传感技术学报，2012，25(8)：1088-1092． CHEN Jin-fei, ZHANG Qi, PAN Meng-chun, et al. Research on geomagnetic anomaly localization based on cubic measurement array[J]. Chinese Journal of Sensors and Actuators, 2012, 25(8): 1088-1092. (in Chinese)

[3] Wiegert R, Oeschger J. Generalized magnetic gradient contraction based method for detection, localization and discrimination of underwater mines and unexploded ordnance[C]∥MTS/IEEE OCEANS 2005. Washington DC, US: IEEE , 2006: 1325-1332.

[4] 张朝阳，肖昌汉，阎辉．磁性目标的单点磁梯度张量定位方法[J]．探测与控制学报，2009，31(4)：44-48． HANG Zhao-yang, XIAO Chang-han, YAN Hui. Localization of a magnetic object based on magnetic gradient tensor at a single point[J]. Journal of Detection & Control, 2009, 31(4): 44-48. (in Chinese)

[5] 张光，张英堂，李志宁，等．载体平动条件下的磁梯度张量定位方法[J]．华中科技大学学报：自然科学版，2013，41(1)：21-24． ZHANG Guang, ZHANG Ying-tang, LI Zhi-ning,et al. Localizing method of magnetic field gradient tensor under carriers moving parallelly[J], Journal Huazhong University of Science & Technology: Natural Science Edition, 2013, 41(1): 21-24. (in Chinese)

[6] 庞鸿锋，朱学军，万成彪，等．基于磁梯度张量和地磁矢量测量的运动式定位方法：中国，201510027060.7[P]. 2015-04-22． PANG Hong-feng, ZHU Xue-jun, WANG Cheng-biao, et al. Movable type location method based on magnetic gradient tensor and geomagnetic vector measurement: China, 201510027060.7[P], 2015-04-22.(in Chinese)

[7] 于振涛，吕俊伟，张本涛．基于海底磁力仪阵列的磁性目标定位方法[J]．武汉理工大学学报，2012，34(6)：131-135． YU Zhen-tao, LYU Jun-wei, ZHANG Ben-tao. A method to localize magnetic target based on a seabed array of magnetometers[J]. Journal of Wuhan University of Technology, 2012, 34(6): 131-135. (in Chinese)

[8] Nara T, Ito W. Moore-Penrose generalized inverse of the gradient tensor in Euler's equation for locating a magnetic dipole[J]. Journal of AppliedPhysics , 2014, 115(17): 17E504.

[9] 庞学亮，林春生，张宁．一种基于磁偶极子模型的潜艇信号检测方法[J]．海军工程大学学报，2011，21(3)：73-76． PANG Xue-liang, LIN Chun-sheng, ZHANG Ning. A new method of signal detection and parameter estimation based on magnetic dipole model[J]. Journal of Naval University of Engineering, 2011, 21(3): 73-76. (in Chinese)

Research on Magnetic Target Location Method Based on a Single Magnetic Gradiometer

JIA Wen-dou1, LIN Chun-sheng1, SUN Yu-hui1, ZHAI Guo-jun2,3

(1.Department of Weaponry Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China; 2.Department of Navigation Engineering, Naval University of Engineering, Wuhan 430033, Hubei, China; 3.Naval Institute of Hydrographic Surveying and Charting, Tianjin 300061, China)

Euler method can be used to realize the accurate positioning of magnetic dipole source. The magnetic gradient tensor data can be calculated using the magnetic field strength data, which is measured by rotating the magnetic gradiometer. A magnetic target location method based on the rotation of a single vector magnetic gradiometer is proposed. A rotating detection model of magnetic gradiometer is established. The influences of rotational angle, inclination angle and baseline length on the positioning accuracy of target are analyzed, which provides a reference for the design of rotating device. The proposed detection method has a higher positioning accuracy in the region near the magnetic target compared with the detection method using an array of seven magnetic sensors.

electromagnetics; magnetic tensor; Euler method; magnetic gradiometer

2017-01-06

国家自然科学基金项目(41374018、41476087)；国家重大科研装备研制基金项目(ZDYZ2012-1)

贾文抖(1990— )，男，博士研究生。E-mail：jiawd163@163.com

林春生(1961— )，男，教授， 博士生导师。E-mail：lcs_and_zh@163.com

TJ61+7

A

1000-1093(2017)08-1572-06

10.3969/j.issn.1000-1093.2017.08.015