一种改进的高铁无砟轨道检测方法
郑 涛,全金谊,徐辛超
(1.辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000;2.济南市勘察测绘研究院,山东 济南 250101)
一种改进的高铁无砟轨道检测方法
郑 涛1,全金谊2,徐辛超1
(1.辽宁工程技术大学 测绘与地理科学学院,辽宁 阜新 123000;2.济南市勘察测绘研究院,山东 济南 250101)
无砟轨道的静态检测通常是沿着轨道线路对轨枕逐个检测,这样做虽然能够满足工程精度的需要但是工作效率较低。文中通过比较不同的插值方法的优缺点,最终选择通过三次样条插值对静态轨道检测的隔轨数据进行处理,并结合贵广高铁检测工程在采用不同的测量方案下,对高铁线路直线段和曲线段的插值结果进行分析。并且用内插后的轨检数据结果与连续测量后得到的轨检数据进行比较,得出不同条件下最有效、最准确的测量与数据处理的实施方案,工程实践证明,文中提出的检测与数据处理手段具有准确性和高效性。
铁路运输;轨道静态检测;无砟轨道;轨道精调;曲线插值
为了保证列车在轨道上安全运行, 铁路部门采用动态检测和静态检测两种方式对铁路轨道进行检查[1]。实际工作中在无砟轨道初期铺轨工程结束以后,就需要对钢轨进行轨道的静态调整检测轨道铺放位置的几何参数是否符合给定的设计要求。无砟轨道的检测数据包括轨道平面偏差、轨道高程偏差、轨道轨向偏差、轨道轨距偏差[2]。国外自动化检测方法一般是利用轨道检测小车来检测轨道的几何状态保证调轨的精确性,例如Lecia公司生产的轨道检测小车。国内也有使用经常用到轨检小车或者是采用常规测量仪器逐轨枕测量,但是国内外针对最原始的轨枕检测数据研究较少,其中比较常见的是使用波形理论,因此,研究如何能够利用较少的检测数据获得全部轨枕点的轨道几何状态偏差,并且保证获得轨检数据的准确性就变得非常有意义。
1 轨道静态检测工作流程
进行轨道检测前需要进行准备工作:轨道静态调整之前需要对施工CPIII控制网进行复测,使CPIII控制点满足无砟轨道精调的要求[3]。进行轨道检测时会给定轨道的里程信息和坐标信息。通过线路线形编辑软件计算得到轨道精调所需要的参数文件,包括中线/参考线文件,竖曲线文件,超高文件。
静态检测的具体工作流程:在轨道检测前向手簿控制端输入设计的线路参数文件和CPIII数据文件,并且确保高精度全站仪和轨检小车以及CPIII棱镜之间能够通视[4];利用6~8个CPIII控制点进行全站仪的后方交会自由设站,瞄准轨检小车棱镜进行轨道几何状态参数的数据采集,测量完成后利用手簿机载的数据处理软件对实测数据与设计线形数据进行比较,计算给出轨道的理论调整量指导施工人员对轨道进行调整;然后进行轨道的第二次轨道几何状态参数的检测,直至达到符合与动态检测的联调联试的标准[5]。
不同测站的建站误差、轨道线路状况以及全站仪测量距离的远近而引起的同一个轨枕几何状态参数偏差的不同,所以为了保证检测数据的精度,相邻的测站间必须有一段搭接的区域。工程中默认的搭接距离大概为15根轨枕。搭接精度限差平面不超过3 mm,高程不超过3 mm[6]。工作区域示意图如图1所示。
2 三次样条插值在轨道检测中的应用
2.1 曲线插值在轨道检测中的应用原理
数值逼近方法通常有两种:一种是根据采样点数据进行函数插值方法,另一种是利用离散数据拟合方法[7]。常见的插值函数有:Lagrange函数插值法、分段三次Hermite函数插值法和三次样条函数插值法等等。
2.1.1 Lagrange插值法
Lagrange插值法对n个离散点的数据进行数值逼近处理,要导出一个n-1次多项式。
(1)
上式为拉格朗日进行插值的n阶公式,q(x)(i=0,1,…,n)称为插值函数的基函数。
轨道检测数据处理中如果采用Lagrange插值可能造成n特别大,这样对于高阶的高次多项式,计算量很大,不适用于工程实际的情况。同时,随着采样点增加插值函数的精度就会降低而产生龙格现象。如果使用低次插值函数进行数据的插值,所得的函数效果又不太理想[8]。
2.1.2 分段三次Hermite插值
三次Hermite定义如下:
(2)
对于分段Hermite插值如果要提高插值精度,那么就需要把插值采样点的间距设置小一点,这样做虽然可以有效地避免龙格现象的发生,但由于Hermite插值只具有连续的一阶导数,得到的插值曲线光滑性并不高。对于高精度的轨道精调数据以及提高工作效率来讲不是太实用。
2.1.3 三次样条插值
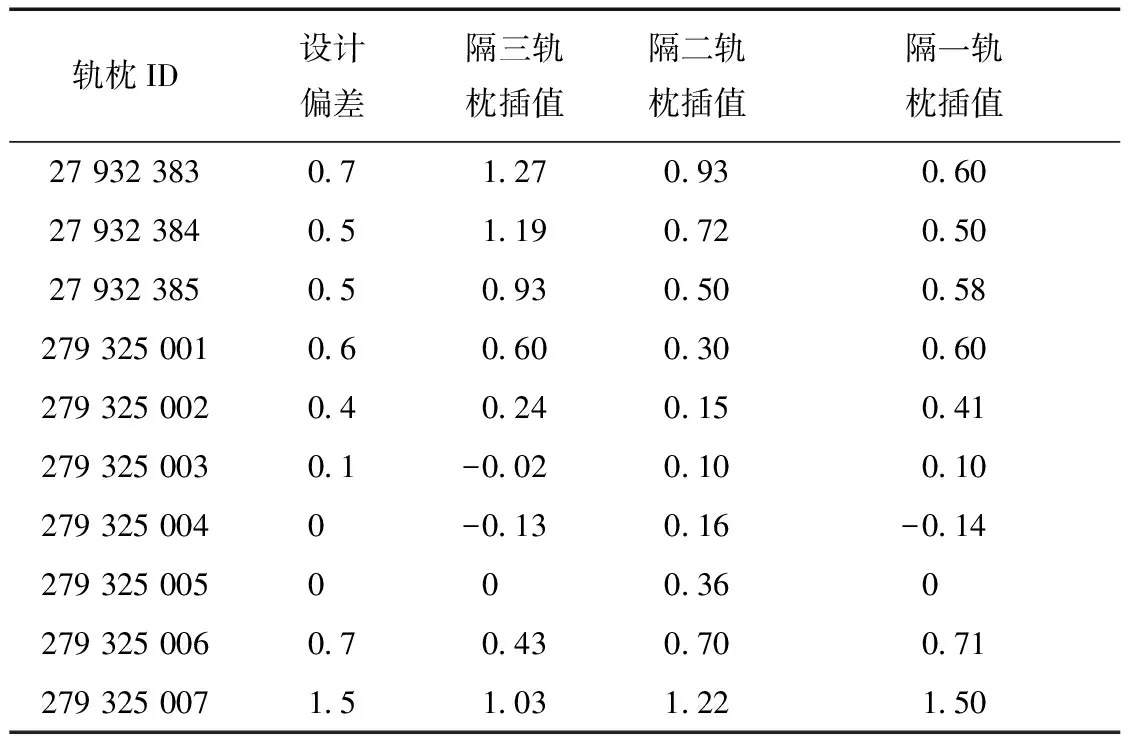
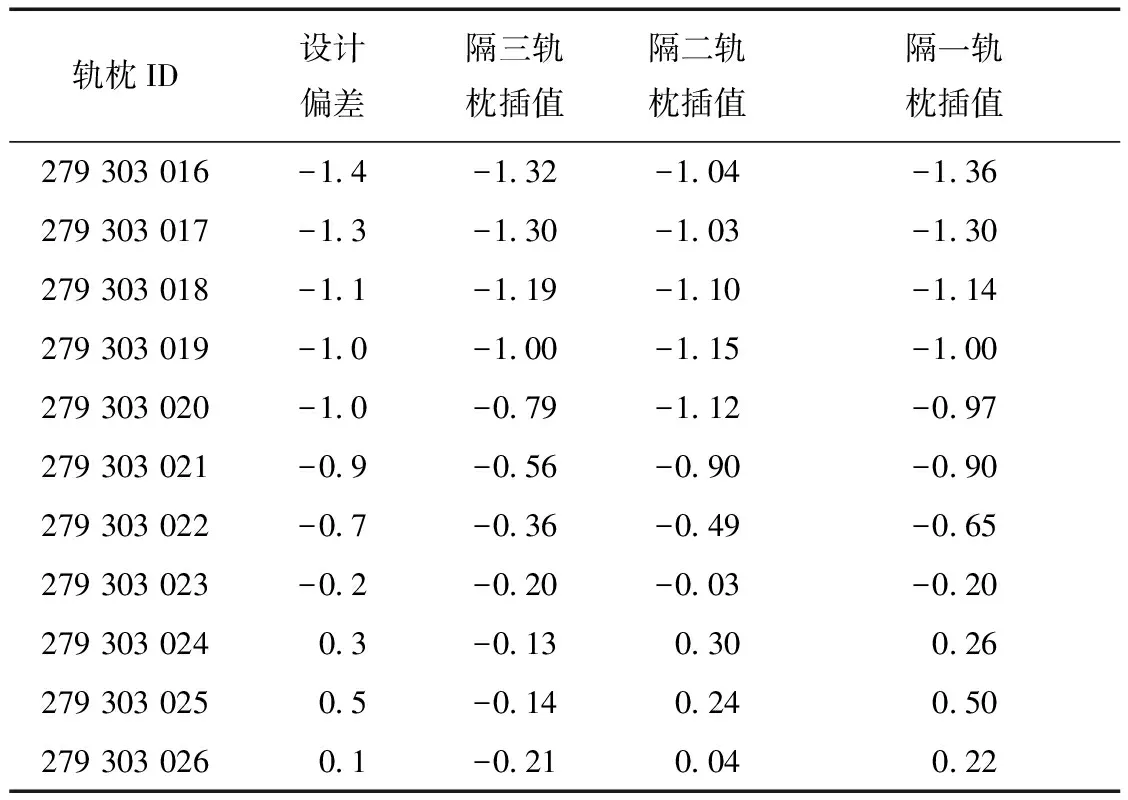
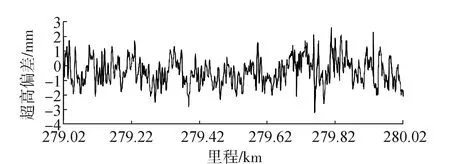
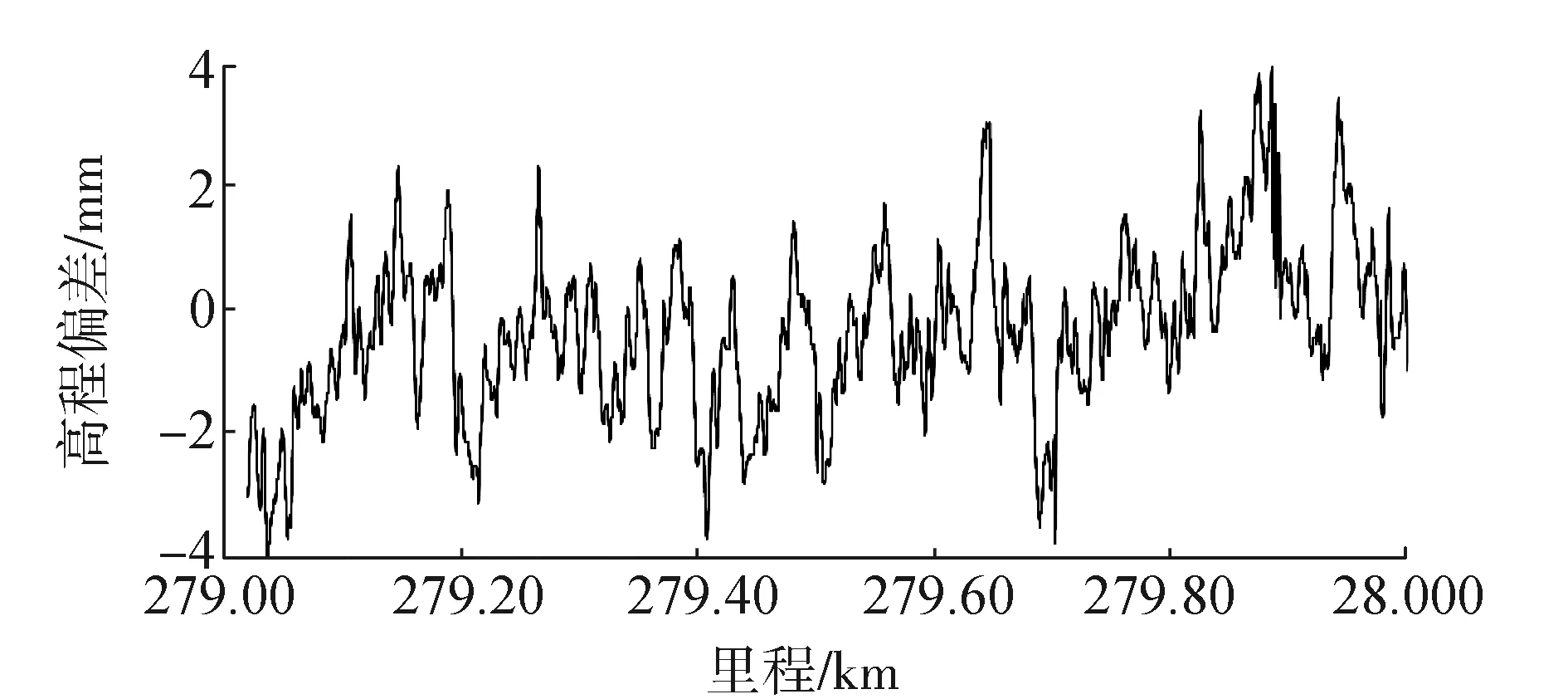
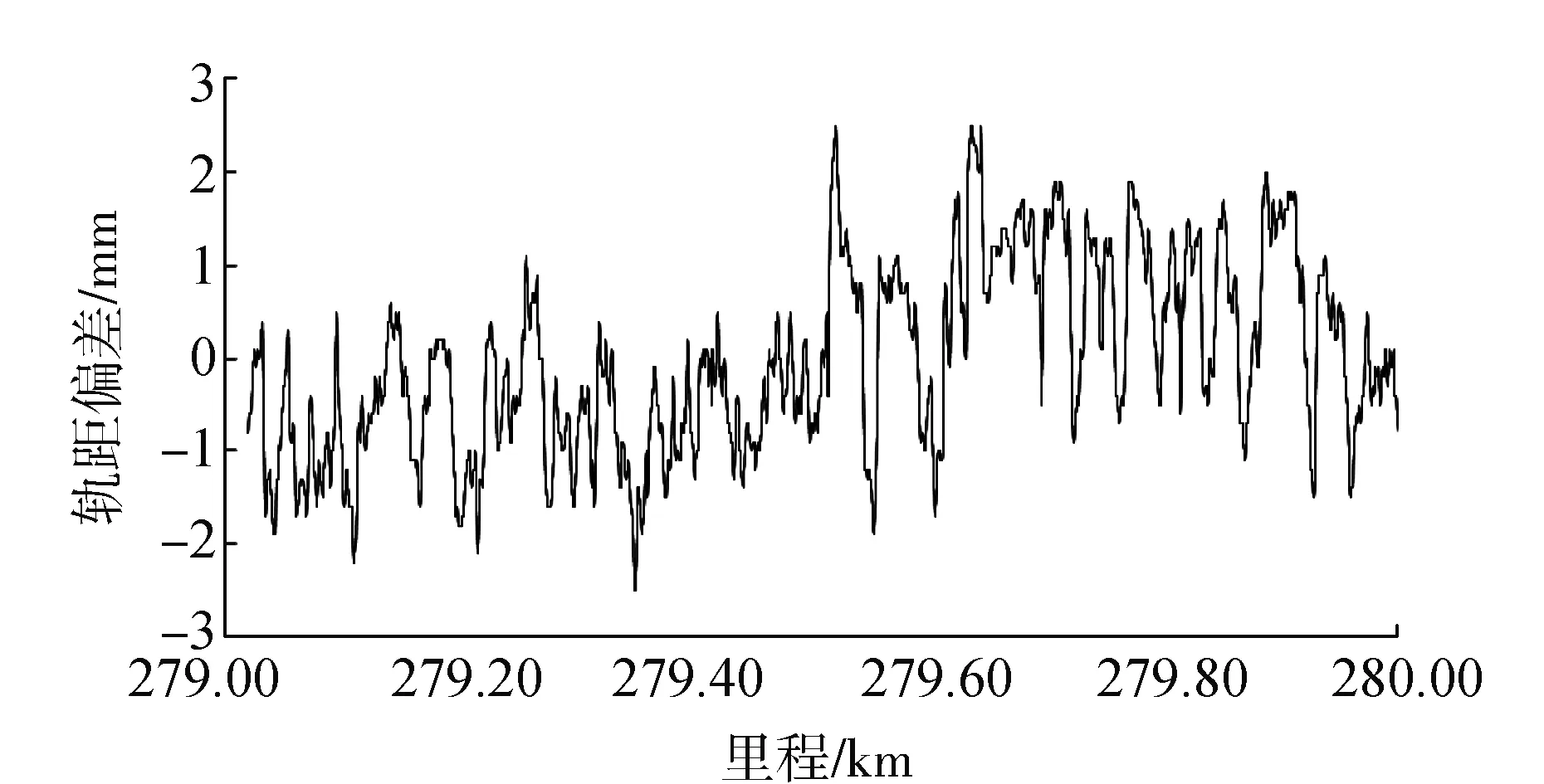
三次样条插值函数可以通过任意多个有限的数据采样点,就能保证插值的曲线函数具有二阶导数良好的连续性。三次样条插值方法简单易行其插值能力很强,其定义为对于数据区间(a,b)上给定的分划区间:a=x0 设一阶导数S′(xi)=Mi(i=0,1,…,n),在区间[xi,xi+1]上由Lagrange插值有 (3) 式中hi=xi-xi-1,再对式(3)进行两次积分,可以得到 (4) 再对上式微分一次得 (5) 由于S(x)在(a,b)上的一阶导数具有连续性,则S(x)在[xi-1,xi]和[xi,xi+1]上的插值点i处具有相同的一阶导数,S′(xi-0)=S′(xi+0)代入式(3)得 (6) 确定三次样条函数的边界条件,[x0,x1]上当x等于x0的时候,代入式(3),可以得到 (7) 当S(0)已知,并由上式,令x=x0,得 (8) 求得的起点边界条件如下: 2M0+a0M1=g0. (9) 同理,得到终点边界条件 (10) 构成了定解问题 (11) 对式(11)进行求解,在每个细化的小区间里建立三次样条插值函数的表达式,就可以得到最终对采样点进行插值的函数曲线。 通过对以上插值曲线的分析,可以得到: 1)Lagrange插值法在数据量大的时候计算量大,还有可能会出现龙格现象,插值误差较大。 2)分段三次Hermite插值得到的函数插值曲线只具有连续的一阶导数,得到的插值的曲线光滑度也不高。 3)三次样条曲线线形光滑,能够较好地反映数据的线形[10],适合轨道检测数据的插值分析处理。 2.2 三次样条插值在在轨道检测中的应用分析 结合贵广高铁的工程轨道检测外业采集数据,按照采样间隔分别设为隔一、隔二、隔三根轨枕,并且分别在直线段、曲线段分析确定三次样条曲线插值法在轨道精调的工程实际中的适用性,计算对轨道检测数据三次样条曲线插值处理的轨枕点数据,相对于实际测值的偏差平均值、中误差。 2.2.1 高程数据插值 1)对直线段的高程数据进行插值处理并分析,得到其相对检测数据的偏差平均值和相对于检测数据的中误差,如表1所示。 表1 直线段高程隔不同数目轨枕插值 mm 由此得出,在进行直线段的高程数据轨道精调时,隔两根轨枕进行测量效果相对于隔一和隔三根轨枕效果较好,插值高程误差平均值为0.01 mm,高程中误差为0.087 7 mm。 2)对曲线段的高程数据进行插值处理并分析,得到其相对检测数据的偏差平均值和相对于检测数据的中误差,如表2所示。 表2 曲线段高程隔不同数目轨枕插值 mm 由此得出,在线路曲线段调轨时隔一根轨枕进行测量相对于隔二隔三轨枕测量效果较好,插值高程误差平均值为0.003 mm,高程中误差为0.067 mm。 2.2.2 轨向数据插值 1)对直线段的轨向数据进行插值处理并分析,得到其相对检测数据的偏差平均值和相对于检测数据的中误差,如表3所示。 表3 直线段轨向隔不同数目轨枕插值 mm 由此得出,在直线段调轨时隔两个轨枕进行测量效果相对于隔一和隔三根轨枕效果好,插值误差平均值为0.023 mm,中误差为0.152 9 mm。 2)对曲线段的轨向数据进行插值处理并分析,得到其相对检测数据的偏差平均值和相对于检测数据的中误差,如表4所示。 表4 铁路道岔隔不同数目轨枕插值 mm 由此得出,在线路曲线段调轨时隔一个轨枕进行测量相对于隔二轨枕测量效果较好,插值误差平均值为0.014 mm,中误差为0.108 mm。 2.2.3 超高数据插值 1)对直线段的超高数据进行插值处理并分析,得到其相对检测数据的偏差平均值和相对于检测数据的中误差,如表5所示。 可以看出,在直线段调轨时,隔两个轨枕进行测量效果相对于隔一个和3个轨枕效果较好,插值误差平均值为0.008 mm,中误差为0.069 6 mm。 2)对曲线段的高程数据进行插值处理并分析,得到其相对检测数据的偏差平均值和相对于检测数据的中误差,如表6所示。 表5 直线段超高数据隔不同数目轨枕插值 mm 表6 曲线段超高数据隔不同数目轨枕插值 mm 在线路曲线段调轨时,隔一个轨枕进行测量,相对于隔二轨枕测量效果较好,插值误差平均值为0.009 mm,中误差为0.016 5 mm。 2.2.4 轨距数据插值 1)对直线段的轨距数据进行插值处理并分析,得到其相对检测数据的偏差平均值和相对于检测数据的中误差,如表7所示。 由此得出,在直线段调轨时隔二轨枕进行测量效果相对于隔一隔三根轨枕效果较好,插值轨距误差平均值为0.001 mm,轨距插值中误差为0.067 3 mm。 2)对曲线段的轨距数据进行插值处理并分析,得到其相对检测数据的偏差平均值和相对于检测数据的中误差,如表8所示。 表7 直线段轨距隔不同数目轨枕插值 mm 表8 曲线段轨距隔不同数目轨枕插值 mm 由此得出,在线路曲线段调轨时隔一轨枕进行测量,相对于隔二轨枕测量效果较好,轨距插值误差平均值为0.016 mm,轨距中误差为0.044 8 mm。 综上所述,通过实验获得的所有插值后得到的数据均符合中误差在0.3 mm以内。所以,三次样条插值得到的数据可以用在轨道静态检测数据的计算中。在实际操作中应该注意基于轨道位置偏差变化平缓、轨道延续不断、静态调整的多次重复性,可以根据情况进行样条曲线插值。直线段进行调轨时可以间隔两轨枕进行测量。在曲线段进行调轨时最好只隔一轨枕或者连续测量。 将数据进行曲线插值处理后获得没有进行检测的轨枕点的轨道几何状态参数,将所有轨枕点的检测数据导入到轨道平顺性评价系统中进行评估,与未做间隔采点处理的原始检测数据的评价结果进行比较。 利用里程279 000至280 000范围内的轨道检测数据进行具体分析,直线段采用隔二轨枕检测曲线段采用隔一轨枕曲线检测,得到外业采集的原始数据并对得到的原始数据进行插值处理。由图2—图5分析可以得到该区段通过间隔采点再经过三次样条插值计算得到的轨道检测数据与未经过间隔采点处理的原始数据反应的线路情况一致,轨道几何状态参数与实测的数据在允许误差范围内。 图2 超高插值结果 图3 高程插值结果 图4 轨向插值结果 图5 轨距插值结果 通过将插值得到的数据导入到平顺性评价系统,与原始数据导入到该系统得出的调整曲线对比可知。曲线插值确实可以应用在轨道静态检测的数据采集过程中,且得到的数据完全可以计算调整量。 本文通过分析不同的插值方法最后采用适合高铁检测数据的三次样条插值算法,将其运用到贵广高铁的工程中并将处理后数据导入平顺性系统进行评价,充分验证了该方法的可行性和有效性。 1)三次样条插值比Lagrange插值法、分段三次Hermite插值法更适合于处理高铁无砟轨道静态检测。 2)通过实测数据论证了高铁静态检测中,对于直线段测量隔三轨枕精度较低应采用隔二轨枕测量方法;在曲线段、道岔的测量过程中由于高铁静态检测数据误差要求较高应采用隔一轨枕或者是连续测量的方法进行。 3)本文通过简化外业观测手段按照实验方案通过三次样条插值获得的数据中误差均在0.3 mm以内,均满足《客运专线无砟轨道铁路工程施工质量验收暂行标准》,对于没有突变情况下相邻两轨枕相对点位误差绝对值不超过0.3 mm的精度要求。 [1] 芮小平,刘仍奎,涂霞蔚,等.基于轨道检测数据的轨道状态评定方法研究[J].中国安全科学学报, 2007,17(4):166-171. [2] 郝亚东,赵杰,樊廷春.基于 GRP1000 的无砟轨道精调测量研究[J].测绘通报, 2013(4):52-55. [3] 何林烜,刘成龙,达乾龙,等.高速铁路轨道控制网高程网测量新方法[J].铁道科学与工程学报,2014(6):137-141. [4] 洪思敏.轨道检测小车测量方法的研究[D].广州:广东工业大学,2015. [5] 中华人民共和国铁道部.高速铁路工程测量规范:TB10601—2009[S].北京:中国铁道出版社,2010:13-15. [6] 刘成龙,杨雪峰.高速铁路轨道基准网平面网精度评定方法[J].测绘科学技术学报,2012,29(6):401-405. [7] 李济民.基于遗传算法的轨道精调系统的设计与应用[D].武汉:武汉理工大学,2012. [8] 陈鹏,陈正阳,李骁.一种新的GPS精密星历插值方法[J].大地测量与地球动力学,2009,29(2):111-114. [9] 林志熙,黄富贵,周景亮.基于三次样条函数的采样点分布方法研究[J].福建工程学院学报,2005,3(3):212-215. [10] 姚连璧,刘春.样条函数与稳健估计在线路线形识别中的应用[J].同济大学学报(自然科学版),2004,32(7):943-946. [责任编辑:刘文霞] An improved method for static detection of unballasted track ZHENG Tao1,QUAN Jinyi2, XU Xinchao1 (1.School of Geometrics, Liaoning Technical University,Fuxin 123000,China;2.Jinan Geotechnical Investigation and Surveying Institute,Jinan 250101,China) The static detection of unballasted tracking is the way of testing the railway sleeper one by one along rail lines, for which it can meet the needs of engineering precision but the work efficiency is low. By comparing the advantages and disadvantages of different interpolation methods, this paper selects three spline interpolations to process the data of the static orbit detection. And combing different measurement schemes of Guangzhou high-speed test engineering, this paper analyses the interpolation results of high-speed straightaways and curve segments. Comparing track inspection data resulting from continuous measurement, the paper obtains the most effective and precise measurement and data processing implementation scheme, which is proved by engineering practice. railway transportation; track static detection; unballasted track; track fine adjustment; curves interpolation 著录:郑涛,全金谊,徐辛超.一种改进的高铁无砟轨道检测方法[J].测绘工程,2017,26(11):49-54. 10.19349/j.cnki.issn1006-7949.2017.11.011 2016-10-09 国家自然科学基金资助项目(41401535,41504030) 郑 涛(1982-),男,博士研究生. P258 A 1006-7949(2017)11-0049-06
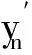
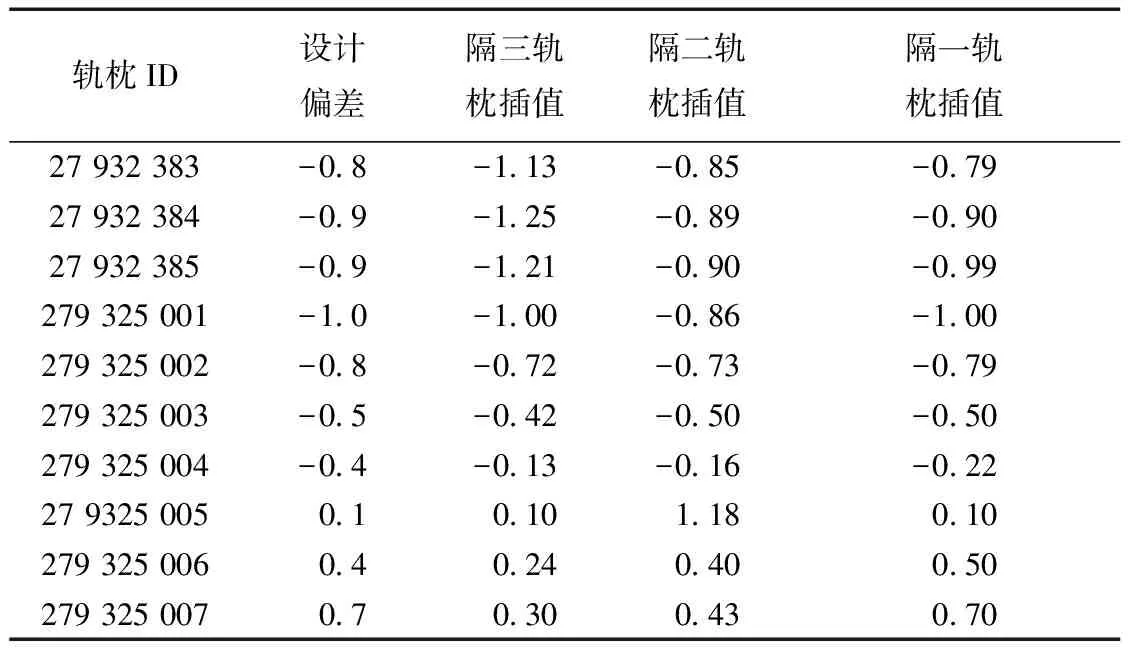
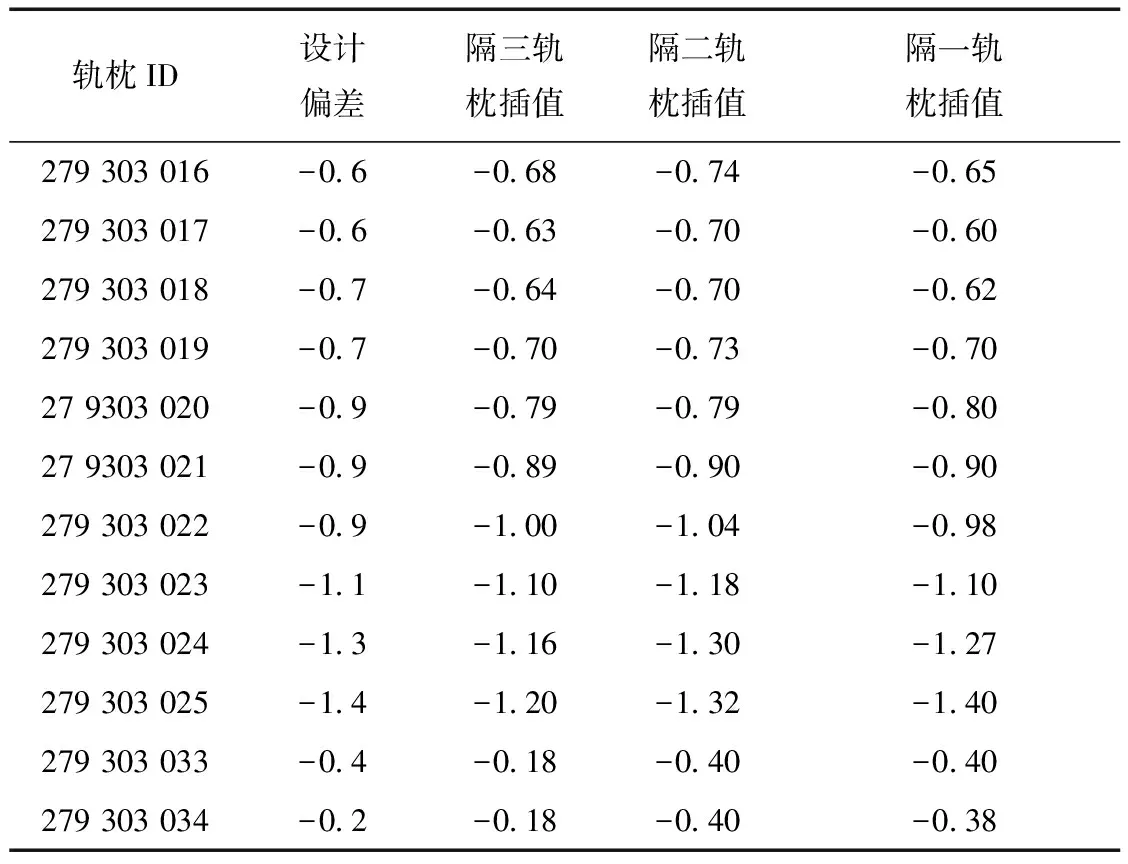
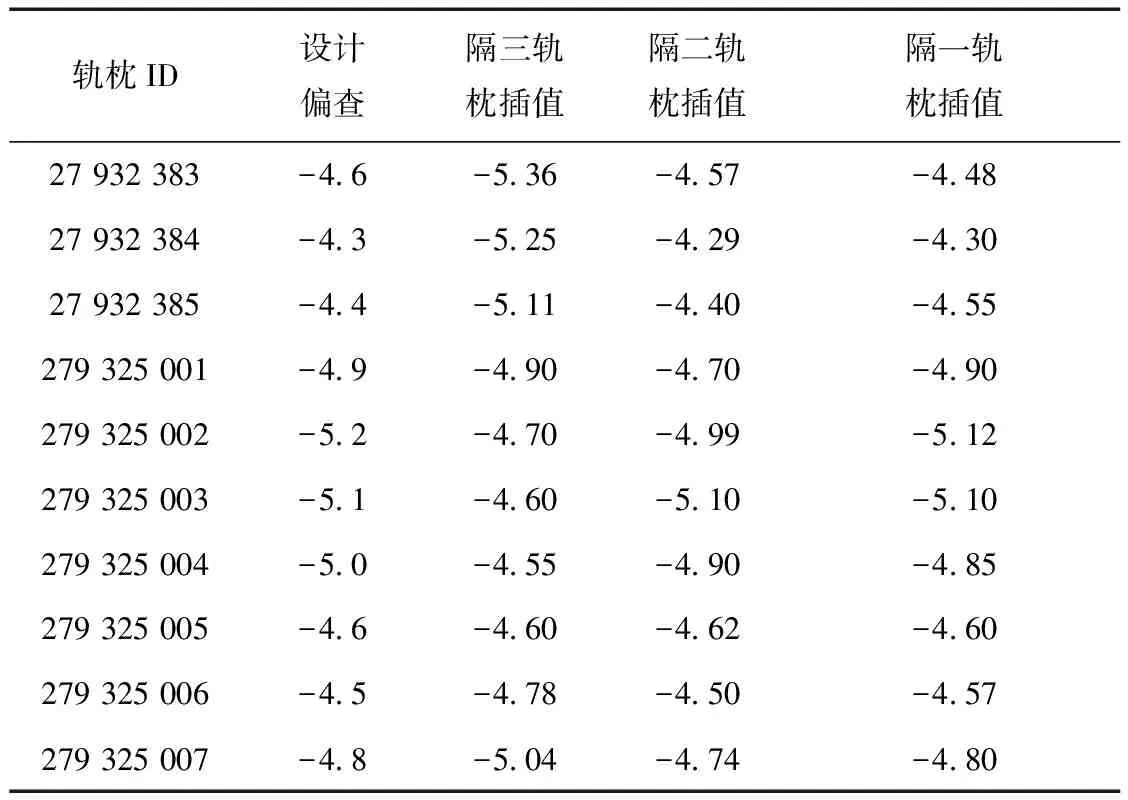



3 工程实例数据处理与分析

4 结束语

