北斗三频非差观测值的电离层周跳探测与修复

赵才新，吴江飞，栗广才

(信息工程大学 地理空间信息学院，河南 郑州 450001)

北斗三频非差观测值的电离层周跳探测与修复

赵才新，吴江飞，栗广才

(信息工程大学 地理空间信息学院，河南 郑州 450001)

针对历元间隔较大或电离层延迟较大的情况，采用两个无几何相位组合与一个最优无几何无电离层组合形成3个线性无关的探测量，将历元间高次差法引用到无几何相位组合探测量中，通过选取合适的探测阈值，使无几何相位组合能够正确探测到较大电离层影响情况下的不敏感周跳。此外，文中采用了一种特殊的无几何无电离组合观测量进行辅助修复，通过两次取整保证了周跳修复的准确性，避免了传统三频周处理中的搜索算法造成错误修复的问题，试验表明，文中算法可以正确探测与修复较大电离层影响情况下不同北斗卫星星座类型的所有小周跳组合以及不敏感周跳组合。

周跳探测与修复；电离层延迟；高次差；北斗三频；小周跳

在GNSS定位中，一般有两种方法处理周跳问题，第一种是引进新的模糊度参数，第二种是对周跳直接探测与修复。然而模糊度参数通常需要较长的时间才能收敛，引进新的模糊度参数无疑会延长收敛时间，因此准确地探测和修复周跳对参数收敛起着关键性的作用。我国的北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)在3个频率上播发信号，为实时周跳探测提供了性能更加优良的非差线性组合[1-3]。对于常规的基于三频伪距/载波组合或三频相位组合周跳处理方法，均假设历元间电离层变化对周跳处理的影响可以忽略不计，但在历元间隔较大或电离层活跃期间，这种假设将不再成立[4-7]。为了避免在电离层活跃时期周跳误判的问题，文献[8]选取了两个无几何无电离层伪距相位和一个弱电离层的无几何组合组成3个线性无关的组合系数对北斗三频数据进行周跳探测与修复，但由于观测量的综合噪声非常大，周跳处理成功率非常低。基于上述问题，本文提出了一种新的周跳探测方法，以适应历元间隔较大或电离层延迟较大时的周跳处理问题。

1 无几何无电离层伪距相位组合

北斗三频伪距/相位组合观测量方程可表示为

Pabc=aP1+bP2+cP3=

(1)

式中:ρ为卫星至接收机的几何距离；βabc,βijk分别为伪距组合观测量和相位组合观测量的电离层延迟数，i,j,k∈Z，a,b,c∈R ，I1为载频f1上的电离层延迟；mabc，mijk分别为伪距组合观测量和相位组合观测量的多路径误差；dabc和dijk分别为伪距组合观测量和相位组合观测量的硬件时延；Nijk和λijk分别为相位组合观测量的模糊度和波长；εabc，eijk分别为伪距组合观测量和相位组合观测量的观测噪声；R,Z分别代表实数集和整数集。构造三频无几何无电离层组合作为三频周跳检验量[7,9]

(2)

需要满足条件

(3)

(4)

(5)

式中σP，σφ分别为以米为单位的伪距观测精度和以周为单位的相位观测精度。由于硬件延迟误差随时间变化缓慢，因此在相邻历元求差时可基本消除硬件延迟项，给出周跳探测公式

(6)

式中:Δφijk=φijk(t1)-φijk(t0)，ΔPabc=Pabc(t1)-Pabc(t0)，则组合周跳的估计精度为

(7)

可根据式(8)判断是否有周跳发生

(8)

当k分别取3和4时表明以99.7%和99.9%的显著性水平判定有周跳发生。

假设北斗的相位精度和伪距精度分别为0.01周和0.3 m对于无几何无电离层伪距/载波组合，在满足条件式(3)、式(4)和式(5)的情况下,搜索到的最优组合(0，1，-1)噪声误差为0.064周，而次优其4倍中误差达到了一周，这将不利于小周跳的探测与修复，基于此问题，本文采用了一种具有平滑作用的特殊周跳探测修复量

(9)

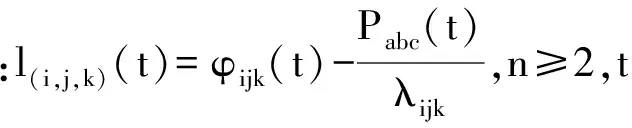
根据式(9)可知，

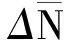
(10)

则ΔNikj正确取整的概率为

(11)

式中f(·)函数的作用是把周跳量固定为n的倍数，由式(11)可知纳伪率与取整成功率分别是关于n的单调递减与递增函数。当n=4时，该修复量的取整成功率为99.99%，已经接近于1，纳伪率也趋近于0，这对周跳的修复非常有利；当n=4时，若以4倍中误差作为探测阈值，会有至少3个探测量被探测出来，由于探测量噪声达到了0.5周，且被探测出的相邻周跳其值仅存在1周的差值，很难确定合理的探测阈值。因此根据以上特点，该探测修复量可以用来作为周跳修复而不参与周跳探测。

2 高次历元差分的三频无几何相位组合

在无几何无电离层伪距相位组合中，随着|i+j+k|的增大，噪声会迅速增大，在无几何无电离层伪距/载波组合中寻找3个较好的线性无关组合是不可行的[1,7]，此外还需要辅助其它组合观测量来进行周跳探测与修复,本文选取的是无几何相位组合探测量。三频无几何相位组合量如式(12)所示。

(12)

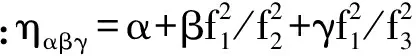
(13)

由式(13)根据误差传播定律可得在电离层延迟误差项忽略不计的情况下，无几何相位组合周跳估值的标准差为

除此之外，由于无几何无电离层周跳探测量无法探测出ΔN1=ΔN2=ΔN3这样特殊的周跳，对于无几何相位组合量的选取必须能够较好地探测出这些特殊周跳组合。因此，无几何相位组合量还需满足

(14)

在满足以上条件的情况下，通过搜索，组合(1，-1，0)与(1，0，-1)对特殊周跳比较敏感，可以用来辅助无几何无电离层伪距相位组合来进行周跳探测。

3 周跳量的探测与修复

对于周跳的探测，本文采用无几何无电离层伪距相位组合(0，-1，1)和无几何相位组合(1，0，-1)与(1，-1，0)构造出3个线性无关的周跳检验量，并对无几何相位组合采用三次差法放大周跳和削弱电离层影响，以便于小周跳的探测与修复。为了进一步削弱电离层残差对周跳探测的影响，对于三次历元差分无几何相位测量取5倍中误差作为探测阈值，然而由于历元间三次差法把周跳放大了一倍，此时纳伪率并不高。

通过前面3个组合探测量可以确定历元发生的准确位置，为了进一步保证周跳修复的准确率，本文采用两个无几何无电离层组合和两个无几何相位组合对周跳进行修复。次优无几何无电离层组合(1，2，-3)当采用如式(9)的探测修复量，并取n=4时，其纳伪率趋于0，而取整成功率为99.99%。若某历元发生周跳，通过对这两个组合的探测量成功取整以后，可以得到3个频率点上的周跳，ΔN1,ΔN2,ΔN3之间的关系，如式(15)所示。

(15)

式中ΔN(0,-1,1),ΔN(1，2，-3)为通过无几何无电离层伪距相位组合(0，-1，1)与(1，2，-3)正确取整后的探测量，因此该式可以认为不含误差。要解出周跳值，还需要采用无几何相位组合，本文采用的无几何相位组合为(1，0，-1)与(1，-1，0)，其探测量关系式如式(16)所示。

(16)

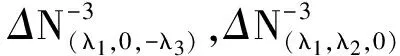
(17)

根据误差传播可算出ΔN1的误差大小为0.09周，由式(11)可知，其四舍五入取整成功率为99.99%，可以对其直接取整，然后把B1上取整后的周跳带入式(17)算出其它两个频率上的周跳，到此，某历元上的周跳探测修复完成。

4 试验与分析

本文算例数据采用MGEX的cut0站于2013年3月17日采集的北斗三频数据，采样间隔为30 s，该站位于电离层变化的显著区域。为了分析各个探测量对小周跳的探测能力，人为地在数据中每隔一些历元加入一些小周跳，对于无几何无电离层组合(0，-1，1)与(1，2，-3)从第40历元开始在观测数据中每隔80历元分别加入周跳组合(0，0，1)与(1，0，0)；对于无几何相位组合(1，0，-1)与(1，-1，0)同样从第40 历元开始在观测数据中每隔80历元加入周跳组合(1，1，1)。如图1(a)所示，无几何无电离层伪距相位组合(1，2，-3)普通探测修复量存在着较大的纳伪率，而当采用如式(9)的探测修复量并取n=4时，如图1(b)所示所有发生周跳的历元均可被探测出来，其值被放大了4倍，且其最大值均不超过6，因此很容易将其正确修复。通过图2可知，在电离层影响较大的情况下，无法探测与修复(1，1，1)这样的小周跳，然而经过历元间三次差后，在放大小周跳的同时电离层残差大部分被削弱，当取5倍中误差作为探测阈值时，小周跳全部被探测出来，而且不存在纳伪现象。

图1 无几何无电离层伪距相位组合探测修复量

图2 无几何相位组合探测量

为了进一步地验证该方法对周跳探测与修复的能力，人为地在观测数据中加入(1，1，1)以内的所有周跳组合以及对无几何相位组合(1，0，-1)来说不敏感的周跳组合(59，48，48)、无几何相位组合(1，-1，0)不敏感的周跳组合(31，24，24)9个周跳组合用本文方法进行探测与修复，其探测与修复结果如表1所示。在表1中第一、第二与第三探测量分别指无几何相位组合(1，-1，0)历元间三次差探测量、无几何相位组合(1，0，-1)历元间三次差探测量和无几何无电离层组合(0，-1，1)普通探测量，特殊辅助修复量是指无几何无电离层组合(1，2，-3)基于式(9)并取n=4的修复量，从表1中可以看出该修复量能完全被成功修复，进而利用本文的修复方法，可将小周跳与不敏感周跳完全正确修复。

5 结 论

针对无几何相位组合在历元间隔较大和电离层影响较大的情况下，将历元间高次差法应用到无几何相位组合探测量，其在消除电离层的同时放大了周跳，克服了一般无几何相位组合难以探测不敏感周跳的问题。用两个历元间三次差无几何相位组合探测量结合一个较优的无几何无电离层组合探测量，形成3个线性无关的组合探测量，能够在电离层延迟较大的情况下对小周跳进行准确探测。在修复时，本文采用了基于次优无几何无电离层组合的特殊修复量进行辅助修复，通过对无几何无电离层组合两次取整，保证周跳修复的正确率，通过试验可知，采用本文方法可实现对北斗卫星导航系统不同星座1周以内所有周跳的探测与修复以及对不敏感周跳组合的探测与修复。由于周跳探测中最多只用前后各4个历元，探测量均为几何无关量且几乎不受电离层影响，因此本文算法可应用在历元间隔较大或电离层影响较大情况下的三频动态实时非差定位数据预处理中。

表1 周跳的探测与修复

[1] 于兴旺.多频GNSS精密定位理论与方法研究[D].武汉：武汉大学，2011.

[2] 陈品馨，章传银，黄昆学．用相位减伪距法和电离层残差法探测和修复周跳[J].大地测量与地球动力学，2010(2)：120-124.

[3] 黄令勇.GNSS多频数据处理理论与方法研究[D].郑州：信息工程大学，2012.

[4] 姚一飞，高井祥，王坚，等.北斗三频载波值的周跳实时探测与修复[J].中国矿业大学学报，2014，43(6)：1140-1148.

[5] CAI Changsheng,LIU Zhizhao,XIA Pengfei,et al.Cycle Slip Detection and Repair for Undifferenced GPS Observations Under High Ionospheric Activity[J].GPS Solution,2013,17(2):247-260.

[6] BANVILLE S,LANGLEY R B. Mitigating the Impact of Ionospheric Cycle Slips in GNSS Observations[J]. Journal of Geodesy,2013,87(2):179-193.

[7] 黄令勇，翟国君，欧阳永忠，等. 三频GNSS电离层周跳处理[J].测绘学报，2015，44(7)：717-725.

[8] 孙保琪，欧吉坤，盛传贞，等.一种适于Compas、周跳探测的三频数据优化组合[J].武汉大学学报(信息科学版)，2010，35(10)：1157-1160.

[9] 黄令勇，翟国君，欧阳永忠，等.削弱电离层影响的三频TurboEdit周跳处理方法[J].测绘学报，2015，44(8)：840-847.

[10] LIU Zhizhao.A New Automated Cycle Slip Detection and Repair Method for a Single Dual-Frequency GPS Receiver[J].Journal of Geodesy，2011，85(3):171-183.

[11] 王维，王解先，高俊强.CPS周跳探测的方法研究[J].武汉大学学报(信息科学版)，2010，36(6)：689-690.

[责任编辑：刘文霞]

Ionospheric cycle slip detection and repair based on BDS triple-frequency undifferenced observations

ZHAO Caixin, WU Jiangfei, LI Guangcai

(School of Geospatial Information,Information Engineering University, Zhengzhou 450001，China)

In the case of high ionospheric activity or long epoch interval, this paper uses two geometry-ree phase combinations and optimal geometry-free, ionospheric-free code-phase combination to form three nonlinear detections.and repair the cycle slip for compass triple-frequency phase data. The high difference geometry-free phase combination by weakening ionospheric activity as well as the amplifying cycle slip can detect insensitive cycle slip under circumstance of high ionospheric activity or long epoch.In the other hand, this paper presents using one kind of special geometry-free and ionospheric-free code-phase combination aid repairing cycle slip, which ensure correct reparation rate of cycle slip by means of double-rounding and avoids incorrect results caused by traditional search method. At last the observation data of long epoch interval under circumstance of high ionospheric activity are used to conduct the experiment, The result shows that the method presented can detect and repair small cycle slip in the case of high ionospheric activity or long epoch interval for different satellites of compass.

cycle slip detection and repair; ionospheric delay; high difference; compass triple-frequency data; small cycle slip

著录：赵才新，吴江飞，栗广才.北斗三频非差观测值的电离层周跳探测与修复[J].测绘工程，2017，26(11)：23-27.

10.19349/j.cnki.issn1006-7949.2017.11.005

2016-10-26

国家自然科学基金资助项目(41174006)；中国博士后科学基金资助项目(201003772；20100481458)

赵才新(1991-)，男，硕士研究生.

P228.4

A

1006-7949(2017)11-0023-05