中学物理成绩信息熵的计算

刘素伶,朱诗洛,王恩过

(岭南师范学院物理科学与技术学院,广东湛江524048)

中学物理成绩信息熵的计算

刘素伶,朱诗洛,王恩过*

(岭南师范学院物理科学与技术学院,广东湛江524048)

通过对离散型及连续型随机函数的信息熵的分析,提出了信息熵计算的基本方法.研究发现,中学物理成绩具有不同的分布特征,有正态分布、瑞利分布、均匀分布等,有的甚至不能用常见的概率分布函数描述.对这些容量大小不同、分布特征各不相同的样本,都可以得到合适的信息熵,显示了计算方法的广泛适用性.

信息熵;物理成绩;概率分布;计算

1 引 言

熵原本是表征系统能量分布均匀程度或系统内部粒子无序程度或混乱度的一个物理量, 20世纪40年代Shannon在信息论中提出信息熵,用以度量信源的平均信息量[1,2].信息熵的提出大大扩展了熵的内涵,也得到了广泛的研究,取得了许多重大的研究成果,并在自然和社会科学的许多领域中得到广泛的推广和应用[3-7].本文探讨了信息熵的计算方法,得到了中学物理成绩的信息熵,期望对信息熵计算与应用有益.

2 计算方法

考虑一个具有n个可能结果的随机试验X,该随机事件不确定性的大小既可以用概率分布函数来描述,也可以用信息熵的大小来度量.若n个可能结果出现的概率分布为P=(P1,其信息熵可用(1)式计算

若X为连续型的随机变量,该连续变量的信息熵则用(2)式表示

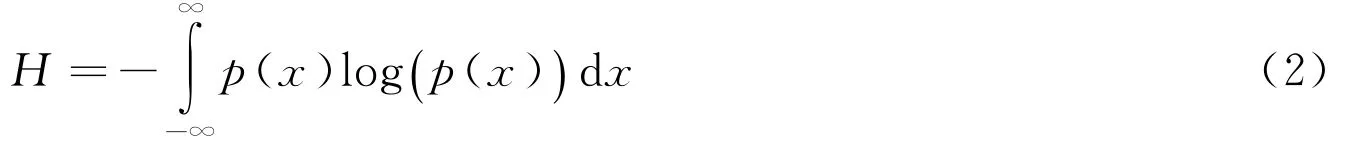
式中,p(x)称为概率分布密度函数.若X的取值区间为[x1,x2,…,xn],将区间该划分成m个等分,每个小区间的长度记为Δx,则X落在第i个小区间的概率为Pi,该小区间的概率密度可表示为,p(xi)=Pi/Δx.考虑到xi→-∞或xi→∞时,p(xi)log(p(xi))→0,概率分布的尾部的影响可以忽视,我们用复合梯梯形公式离散(2)式,得到(3)式.

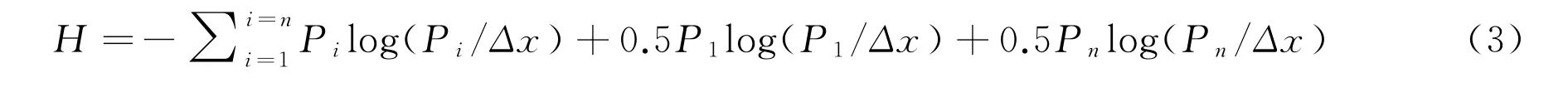
对于一个特定的随机变量而言,不管用什么方法计算的信息熵都应该是相同的,至少是相近的,这是由信息熵的唯一性所决定的.然而,(1)式和(3)式明显不同,因此需要检验哪一种算法更适合于信息熵的计算.为此,我们假设X服从标准正态分布,取Pi=i/(n+1),i=1,2,…n,计算对应的xi,得到具有n个可能结果的随机试验X=[x1,x2,…xn].将X的取值区间划分等距离的m个小区间,小区间的长度Δx=(xn-x1)/m,m为数据分组数.对该随机试验X,分别用(1)式和(3)式计算其信息熵,结果见图1.图1(a)结果说明,用式(1)计算的信息熵随数据分组数m的增加而增加,稳定性差,难以满足信息熵唯一性特征要求.从这个意义上讲,(1)式并不是一个适合信息熵计算的有效方法,尽管这一方法也常常得到了应用[2].换句话说,在用(1)式计算的信息熵时,合适的数据分组数m的确定极为重要.

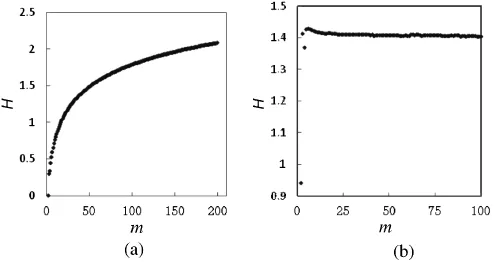
图1 信息熵计算方法比较

从图1(b)可以看出,当数据分组数即m值增加吋,计算的信息熵最初不稳定,表现为快速增加和波动,但当m增至10之后,H值虽然仍有波动且趋势向下,但基本上在非常小范围内波动,比如m为10～100时,H值其波动范围在1%左右;可见用(3)式计算的信息熵具有较好的稳定性,因此更适合于信息熵的计算,因此后续信息熵的计算过程仅采用(3)式进行.

需要指出的是,由于在(3)式推导过程中并没有限定随机变量的具体的分布函数,故所有分布的随机变量都能使用,即使我们并不清楚它的随机概率分布函数的具体表达形式.另外,相比与(2)式,(3)式忽视了概率分布的尾部的影响,因此计算结果可能会偏小一些.但在样品容量n较大时,这种分布尾部的影响会大大降低.

3 计算结果与讨论

为了探讨中学生物理成绩的信息熵,我们以收集的几所中学的物理成绩做为样本,探索不同样本大小、不同概率分布特征的随机变量的信息熵.其中,样本A、B为中山市古镇高级中学2016年9、10月月考物理成绩,样本C、D为四会龙莆学校2016年两次周考物理成绩,样本E为罗定中学2017高三理科一模成绩物理成绩,样本F为罗定城东学校2017高三级学生一模物理成绩,样本G为罗定城东学校2016高一第一学期期末考试物理成绩,样本H为2016电白高级高级中学高一市统考物理成绩.所有的计算过程都在MATLAB软件上进行.

3.1 物理成绩的分布特征

物理成绩的分布特征与其数字特征密切相关,表1给出了研究对象即几所中学的物理成绩的数字特征.表中平均值反映了考卷对考查学生的学习效果适应性,用标准差描述成绩的集中或离散情况.样本A～D平均值较为合理,在60分左右,试题难易适当;其他样本的平均值过低,表明考题对于考生很难.样本的标准差反映学生的学习成绩的离散情况,其值在11至22之间,变化幅度不大.

表1 中学的物理成绩的数字特征

偏度系数S反映了学生考试成绩分布的对称性,S=0为对称分布,S≠0为偏态分布,其中S＞0为正偏态分布,S＜0为负偏态分布.表1显示,样本B～D的S接近0,可以看成为对称分布,这说明考生成绩较好,试题难易适当、考试成绩能够较好反映学生的真实的学习效果.样本A为偏度系数为-0.7181＜0,学生的成绩是负偏态分布的,曲线峰向右偏移,这说明考生成绩偏高,试题偏易、难度偏低,难度较低的项目比例偏大.样本H为偏度系数为1.2104,学生的成绩是正偏态分布,曲线峰向左偏移,这说明试题难度偏高,考生成绩偏低.

峰度系数K反映了分布峰的高低或宽狭.偏度系数S和峰度系数K用于检验考试成绩的分布规律.比如,S接近0、K接近3.0的样品更接近正态分布.因此,样本C、D样品更接近正态分布,其中C样本的QQ曲线(见图2)接近一条直线,就能直观证实了C样本的正态分布的特点.其他样本的偏度系数S或峰度系数K偏离正态分布较大,为了确定这些样本的分布,也可用样本数据分布的分位数与所指定分布的分位数之间的关系曲线来进行检验的,若所有点基本分布在一条直线的附近,就可以初步判定该样本服从相应的分布.样本B的分布特征符合均匀分布函数的特点,其累积概率分布与学生成绩接近线性关系,见图3.

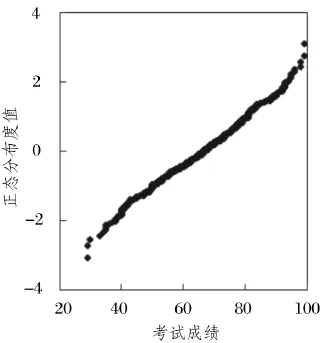
图2 样本C的正态分布QQ图

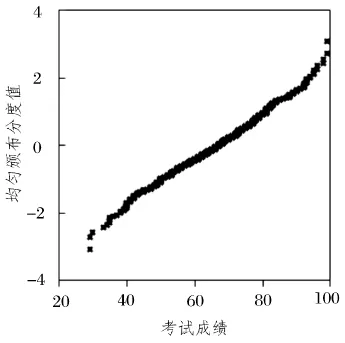
图3 样本B的均匀分布QQ图

如果用样品的学生成绩与均值为0、h=1的瑞利分布分位值作图,可以检验该样本是否为瑞利分布;对样本E,结果见图4,图4说明样品E基本符合瑞利分布.同理,也可证实样品F基本符合瑞利分布.

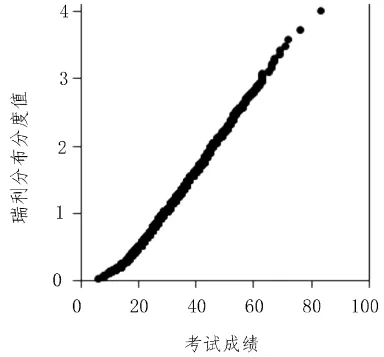
图4 对样本E的瑞利分布QQ图

A、H样本的偏度系数大,为非对称分布,与常见的概率分布函数的特征差异较大,用各个概率分布函数绘制的QQ图的线性也不佳,因此这两个样本的概率分布函数及分布特征尚不清楚,需要进一步研究.

3.2 物理成绩的信息熵

用(3)式计算所有样本在不同m值下的信息熵,结果如图5所示.图5说明,在m大于10后,所有样本的信息熵都具有较好的稳定性,在m=5～40之间信息熵波动幅度不超过1%,因此,用公式(3)计算中学生物理成绩的信息熵是可行的.

图5 物理成绩的信息熵

在m=20时计算的信息熵见表2.从表2可以看出,不同样品的信息熵各有不同,其中样本B的信息熵最大,为1.8827;而样本F的信息熵最小,仅为1.6339.我们知道,信息熵的大小反映了样本不确性的大小,从物理意义上讲,它与标准差一样都与不确定度有关,因此两者之间必然存在一定的关联度.比较表1中的标准差与表2的H值可以发现,标准差大的样本,其H值常常也较大.比如,样本B的信息熵和标准差都是所有样本中最大的.但信息熵变化幅度要远远小于标准差,在二者也不是简单的线性关系,甚至大小次序也不同,如图6所示,这反映了信息熵和标准差的显著区别.

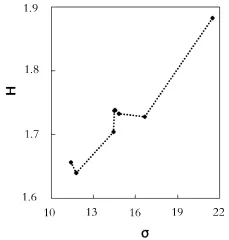
图6 物理成绩的标准差与信息熵的关系

表2 计算的物理成绩的信息熵

尽管信息熵和标准差都可以反映系统的紊乱性和不确定性,而且信息熵常常是标准的单调递增函数,但这一递增关系仅对相同的分布函数是准确的,对不同的分布函数则未必适用.标准差与随机变量的二阶矩特征有关,适用于概率分布为对称的情况;而信息熵则可以表达随机变量的多阶矩特征,对随机变量的分布没有对称性的要求,能更好地描述系统的不确定性,适用性更强[6].如前所述,本研究所用的8个样本,既有对称分布也有非对称分布,其分布特征差异较大,因此用标准差来度量样本的离散特性或不确定性显然是不够的,也是不准确的;而信息熵度量方法使不同样本之间的比较成为可能,这也是信息熵方法能够得到广泛使用的重要原因.

4 结 论

本文通过对离散型及连续型随机函数的信息熵的分析,提出了信息熵计算的基本方法.研究发现,中学物理成绩具有不同的分布特征,有正态分布、瑞利分布、均匀分布等,有的甚至不能用常见的概率分布函数描述.对这些容量大小不同、分布特征各不相同的样本,都可以得到合适的信息熵,显示了这一计算方法的广泛适用性.

[1]C.E.Shannon.Themathematicaltheoryofcommunication[J].BellSystemTechnicalJournal,1948 (27):35-38.

[2]张继国,辛格.信息熵:理论与应用[M].北京:北京水利水电出版社,2012.

[3]黎爱兵,张立凤,王秋良.基于非线性误差信息熵理论的大气多变量系统可预报性分析[J].中国科学:地球科学,2014,44(7):1544-1555.

[4]孙海蓉,王蕊,耿军亚.基于信息熵的BP网络在热工系统建模中的应用[J].系统仿真学报,2017,29 (1):226-233.

[5]薛慧君,张杨,吕昊,等.基于信息熵估计的生物雷达弱周期信号识别技术研究[J].中国医疗设备, 2017,32(1):22-25.

[6]赵秀菊.风险的两种度量方法——信息熵与方差[J].襄樊学院学报,2010(2):12-15.

[7]陈小军,黄敬频.基于信息熵的教学效果比较评估模型[J].广西民族大学学报(自然科学版),2013,19 (1):104-108.

CalculationoftheInformationEntropyoftheExamination ScoresofPhysicsinMiddleSchools

LIUSuling,ZHUShiluo,WANGEnguo
(SchoolofPhysicsScienceandTechnology,LingnanNormalUniversity,Zhanjiang,Guangdong524048,China)

Thesamplesinourstudyaretheexaminationscoresofphysicsinmiddleschools.Anew methodfortheinformationentropycalculationispresentedbyusingthediscretizationoftheinformation entropyofcontinuousrandomvariables,andwasappliedforthecalculationoftheinformationentropyof thesamples.Thedistributionofthesampleswasalsodiscussed.Itisshowedthatthesescoresdonotobey thesamedistribution,suchasthenormaldistribution,Rayleighdistribution,anuniformdistributionfunction,andsoon.Itisalsoshowedthatthepresentmethodcanbeusefulinthecalculationoftheinformationentropyofthesampleswithdifferentsamplesizeanddistribution.Soitisveryusefulforthecalculationoftheinformationentropyofthesamplesinotherfields.

informationentropy;physicsscores;probabilitydistribution;calculation

G421

A

1006-4702(2017)03-0073-06

2017-04-21

刘素伶,女,岭南师范学院2013级物理学本科1班学生.

* 通讯作者.