基于FFT加窗插值算法的应用研究

刘旭东，赵迎春，张艳芬

(营口职业技术学院，辽宁营口115000)

【应用研究】

基于FFT加窗插值算法的应用研究

刘旭东，赵迎春，张艳芬

(营口职业技术学院，辽宁营口115000)

快速傅里叶变换(FFT)算法被广泛应用于电力系统谐波检测，但频谱泄漏、栅栏效应一直是影响测量准确性的重要因素，为此提出了一种FFT加窗插值算法．通过加窗函数、插值修正函数，对FFT算法进行优化，并利用谐波分析的试验实例进行了验证，计算结果表明：加窗加插值FFT算法，可以提高谐波检测精度，达到测量要求，满足电力系统谐波检测需求．

电力系统谐波分析；FFT；窗函数

0 引言

随着高压直流输电技术和新能源发电技术的采用，电气化机车、电动汽车的快速发展，以及工矿企业大量调速设备、换流技术的使用等，电网谐波畸变率升高，超出电力质量指标要求，对电网运行带来极大的危害[1～3]．近些年，谐波治理一直是研究热点，而谐波检测又是其中重要的技术难点．电力谐波的测量技术，通常采用快速傅里叶(FFT)算法实现，但使用过程中采样数据的截取造成的栅栏效应、频谱泄漏等问题，会导致采样数据精确度不高，不能满足谐波测量的要求．

本文提出了一种基于FFT加窗插值的算法，应用于电力系统谐波检测．研究选取一种最适合电力系统谐波检测的窗函数，并通过近似插值对FFT的结果进行修正，最后通过MATLAB仿真验证算法的有效性．

1 算法原理

1.1 频谱泄露和栅栏效应

在谐波测量过程中，SCADA系统采集电流、电压模拟信号，再通过A/D转换得到数字信号；在这个数据截断的过程中，当同步采样时(即采样时间长度等于原信号周期的整数倍)，运算数据显示不受频谱泄漏影响；而当非同步采样时，采样频率不能有效完整地分辨测量信号，就产生了栅栏效应．

快速傅里叶(FFT)加窗插值算法是一种优化算法，可以对FFT产生的栅栏效应、频谱泄漏问题有效控制．窗函数尤为重要，对不同的测量对象，应采用不同的窗函数．论文仿真试验采样以电气信号测量效果较好的汉宁窗为例，谐波测量中频谱泄漏得到很好的抑制．

1.2 加窗插值FFT算法

将测量信号用cosine正弦量表示：

(1)

式中f为频率，A为幅值，φ为相位，p为最高谐波次数．对上式离散处理，得到频谱为：

(2)

若有离散窗W(n)，其频谱W(ejω)可表示为：

W(ejω)=W0(ω)·e-jcω

(3)

式中W0(ω)为一实函数，C为一实常数．加窗函数后的离散频谱为：

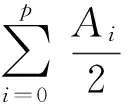
(4)

用DFT可求出XW(n)的离散谱XW(k)，抽样的结果为：

XW(k)=XW(ejω)|ωkΔw，k=0,1,2,…，N-1

(5)

由于考虑不同步问题，截取窗不一定为采样信号周期的整数倍，可设：

(6)

i次谐波表示为：

(7)

其中，ki、λ1分别

ki=ik1，λi=iλ1

(8)

对于i =1,2,… p，由式(7)容易得到

ωi=(ki+λi)Δω

(9)

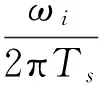
(10)

从式(9)、(10)可知，λi称为频率校正量．对于第i =l次谐波，如果窗W(n)的幅频特W0(ω)满足

W0(klΔω+ωi)=0，i=1,2,…，p

(11)

W0(klΔω-ωi)=0，i=1,2,…，p;i≠1

(12)

当ω=klΔω处，各次谐波含量正、负频率分量都为零，频谱分析不受频谱泄漏影响．此时，由式(4)、(5)、(9)有：

(13)

(14)

arg[XW(kl)]=CλiΔω+φi

(15)

用离散傅里叶变换(DFT)，得到XW(kl),l次谐波参数为：

fl=(kl+λl)Δf

(16)

Al=2|XW(kl)|/[W0(-λlΔω)]

(17)

φl=arg[XW(kl)]-CλlΔω

(18)

1.3 三次样条插值算法

论文采用三次样条函数插值修正[4、5]，计算量不大，稳定性能好，不但能保证信号函数分段的连续，还能保证一阶和二阶导数也是连续的，使函数具有很好的平滑性．以(ti,yi)为插值点，三次样条函数为：

(19)

式中hi=ti+1-ti．

通过加窗插值FFT计算，求得电气信号中基波和各次谐波参数，具有较好的计算精度．

2 仿真计算

仿真计算通过MATLAB数值计算软件实现，编写程序三次样条函数，通过FFT算法加窗插值修正计算仿真．

通过选用不同窗函数，发现汉宁窗测量效果最好．以下列试验数据仿真为例，待测电气各次谐波幅值为：12，4，3，0.5，0.3，0.1，0.05．实例仿真结果见表1，分析结果可知幅值误差修正效果达到0.1%，基本达到谐波检测要求．

表1 汉宁窗修正谐波幅值信号比较

信号幅值(Amplitude)n次谐波1234567FFT校正算法11.75433.77652.81230.41120.31020.08900.0405汉宁窗插值修正11.98393.99232.98550.49610.29420.09770.0483

这说明加汉宁窗和三次样条插值修正FFT算法可以进一步减少谐波间的能量泄漏，从而提高计算精度．

3 结论

提出一种快速傅里叶变换(FFT)算法，应用于电力系统谐波检测．通过对FFT加窗插值的运算分析，得到相应的频谱结果，得出此算法对电力系统谐波检测数据的准确度有明显提高．此算法可以用于电力系统二次回路测量、保护装置测量以及电力计量中，也可以用于其他领域中，具有实用价值．

[1]肖雁鸿，毛筱，周靖林，等．电力系统谐波测量方法综述[J]．电网技术， 2002，26(6)：61-64．

[2]丁玉美，高西全.数字信号处理[M].西安：西安电子科技大学出版社，2001.

[3]祁才君．数字信号处理技术的算法分析与应用[M]．北京：机械工业出版社，2005．

[4]Ignacio Santamaria-Caballero, Carlos J.Pantaleon-Prieto,Jesus Ibanez-Diaz,etal．Improved procedures for estimating amplitudes and phases of harmonics with application to vibration analysis[J]．IEEE Transactions on Instrumentation and Measurement, 1998，47(1)：209-214．

[5]KINCAID D，CHENEY W.数值分析[M].王国荣，俞耀明，徐兆亮，译.北京:机械工业出版社，2005.

(审稿人 马文龙 邓景茹，责任编辑 王 巍)

Applied research on windowed interpolation algorithm on FFT

LIU Xu-dong, ZHAO Ying-chun, ZHANG Yan-fen

(Yingkou College of Vocational Technology, Yingkou Liaoning 115000)

Fast Fourier transform (FFT) algorithm has been widely used in the detection of power system harmonic. But the spectral leakage and fence effect have always been the key factor of influencing the accuracy of measurement. The paper proposes FFT windowed interpolation algorithm, which not only optimizes the FFT algorithm by adding window function and interpolation correction function, but also verifies the harmonic analysis. The computing result shows that the FFT algorithm based on windowed interpolation algorithm can improve the accuracy of harmonic detection and meet the requirements of measurement and electrical system harmonic detection requirement.

power system harmonic analysis; FFT; windows function

2016—12—20

刘旭东(1979-)，男，辽宁营口市人，讲师，主要从事电力系统电能质量方向研究．

辽宁省“十三五”规划高教研究课题(GHYB160232)

TM933

A

1008-5688(2017)01-0078-03