基于离散模型的内超环面齿轮干涉检验方法
洪 玫 姚立纲
福州大学机械工程及自动化学院,福州,350116
基于离散模型的内超环面齿轮干涉检验方法
洪 玫 姚立纲
福州大学机械工程及自动化学院,福州,350116
针对内超环面齿轮齿面加工局部和全局干涉现象,提出一种干涉检验方法,有效地避免了加工干涉。通过干涉检验面簇的引入和干涉检验线簇的构造,将内超环面齿轮齿面和刀具扫掠体离散化。运用内超环面齿轮齿面和刀具扫掠体离散模型,通过截平面处刀具中心的求解,确定内超环面齿轮齿面加工局部和全局干涉区域。通过实例分析进一步验证了内超环面齿轮齿面加工干涉检验方法的可行性。
超环面行星蜗杆传动;内超环面齿轮;复杂曲面;干涉检验;离散建模
0 引言
超环面行星蜗杆传动由中心蜗杆、行星蜗轮、内超环面齿轮、行星架以及滚动体组成[1]。该系统具有优良的传动性能,但这些性能必须以较高的加工精度来保证。内超环面齿轮是系统中的关键零部件,其齿面是复杂的空间曲面,由于齿面形状的特殊性,故在利用球头刀三轴数控加工齿面局部内凹区域的过程中,若刀具半径选取不合适,易造成齿面过切和欠切(即局部干涉),并出现刀具与内超环面齿轮齿面非加工区域碰撞的现象(即全局干涉现象),从而影响加工精度。
目前尚无关于内超环面齿轮齿面加工干涉问题的报道,但是有不少学者针对复杂曲面在加工过程中出现的干涉现象进行了大量的探讨和研究。DING等[2]通过对加工表面几何形状的分析以及模具表面和刀具表面主曲率的计算和比较,有效地检测出三轴模具数控加工中的干涉区域。李艳霞等[3]给出了几种常见刀具扫掠体与毛坯仿真求交的运算公式,通过数控仿真加工模型的建立和交点的求解进行仿真干涉判断。DING等[4]提出了基于包围盒和八叉树的五坐标数控加工自由曲面的干涉检测方法,能有效地减小计算量,提高检测效率。曾志迎等[5]对复杂曲面进行划分,通过环形刀五坐标轴加工模型的建立、刀具最佳尺寸的选取和刀具姿态的改变来避免干涉,从而生成复杂曲面环形刀无干涉刀具路径。李万军等[6]通过曲面干涉检测点和刀具局部坐标系的坐标变换来进行全局干涉检测,判断曲面点是否落在刀具半径范围内来确定干涉点。杜娟等[7]运用曲率匹配原则选取刀具半径,并采用网格点来快速生成检测区域和检测点,保证在接触点处沿任何方向刀具和被加工表面之间不发生干涉。王国勋等[8]通过计算曲面上的点在刀具局部坐标系中刀具投影区域内的坐标值与刀具的坐标位置关系来判断是否发生干涉。AHMET[9]提出了基于参数区域的检测区域和检测点的确定方法,并通过计算切触点与检测点连线的最大倾角来判断是否有干涉发生。文献[10-12]研究了垂直于刀具进给方向的法截面内刀具同加工曲面的几何啮合状态,通过检测刀具和切触点处的曲面曲率是否匹配来进行局部干涉的判断,并通过调整刀具尺寸或刀具姿态来消除干涉现象。
为了有效地检验出内超环面齿轮齿面加工过程中出现的局部和全局干涉区域,从而更好地实现复杂曲面的数控加工,并保证较高的加工精度,本文提出了一种干涉检验方法,能较好地对内超环面齿轮齿面加工局部和全局干涉区域进行检验。
1 干涉检验面的引入和内超环面齿轮齿面离散建模
图1所示为剖视的内超环面齿轮三维实体模型,它由螺旋齿面、旋转曲面和两个端面组成。内超环面齿轮齿面是一种复杂的空间曲面,运用数值方法进行干涉检验计算时难度较大,本文引入与内超环面齿轮轴线垂直的干涉检验面簇与内超环面齿轮齿面接触线簇(图2),求交提取齿面离散数据点,建立内超环面齿轮齿面离散模型。

图1 剖视的内超环面齿轮三维实体模型和单个螺旋齿面Fig.1 Section of stationary internal toroidal gear solid model and single spiral tooth surface

图2 干涉检验面簇和内超环面齿轮齿面接触线簇Fig.2 Interference detection plan cluster and stationary internal toroidal gear tooth surface contact line cluster
根据内超环面齿轮齿面方程[13],将滚珠参数v的取值区间[-π/2,π/2]离散成m个角度,每个角度对应一条齿面接触线,这样内超环面齿轮齿面就被离散成m条接触线。n个干涉检验面与齿面m条接触线相交,可获得m×n个交点坐标,这些交点构成了内超环面齿轮齿面离散数据点。通过改变干涉检验面的个数n和离散角度m,可控制内超环面齿轮齿面离散模型的精度。
2 干涉检验线的构造和刀具扫掠体离散建模
以球头刀三轴数控加工内超环面齿轮齿面为例,将球头刀模型简化成由一个圆柱体和一个半球体组成,当球头刀从一个刀位点运动到下一个刀位点时形成刀具扫掠体模型,如图3所示。T1、T2分别为两个相邻刀位点刀具中心的位置,通过内超环面齿轮齿面离散数据点G(xG,yG,zG)构造与z轴平行的干涉检验线,过干涉检验线作与平面T1T2T3T4垂直的截平面,与刀具扫掠体相交,由此将刀具扫掠体离散成由截平面簇组成。内超环面齿轮齿面离散数据点决定了干涉检验线的位置以及截平面的个数和间距。

图3 刀具扫掠体离散模型Fig.3 Tool scanning body discretization model
3 内超环面齿轮齿面加工干涉检验[14]
3.1 截平面处刀具中心的求解
如图4所示,截平面与平面T1T2T3T4相交的交线可认为是此处刀具的轴线,设两个相邻刀位点刀具中心T1(xT1,yT1,zT1)、T2(xT2,yT2,zT2)在oxy平面上的投影点分别为T1xy、T2xy,
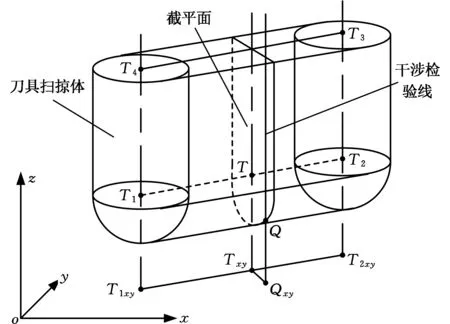
图4 刀具扫掠体截平面处刀具中心求解Fig.4 Solution of the cutting plane tool center
截平面处刀具中心T(xT,yT,zT)在oxy平面上的投影点为Txy,干涉检验线与刀具扫掠体球头部分的交点Q(xQ,yQ,zQ)在oxy平面上的投影点为Qxy。
直线T1xyT2xy的方程为
(1)
直线TxyQxy与直线T1xyT2xy垂直,根据式(1)可求得直线TxyQxy的斜率
(2)
直线TxyQxy的方程为
y-yG=kTxyQxy(x-xG)
(3)
联立式(1)和式(3)即可求得直线TxyQxy与直线T1xyT2xy的交点Txy的x、y坐标值,即截平面处刀具中心T的x、y坐标值xT、yT。
直线T1T2的方程为
(4)
将截平面处刀具中心T的x、y坐标值xT、yT代入式(4),即可求得刀具中心T的z坐标值zT。
3.2 局部干涉检验
如图3所示,干涉检验线通过内超环面齿轮齿面离散数据点G(xG,yG,zG),则干涉检验线的方程为
(5)
如图4所示,干涉检验线与截平面的交点Q与刀具中心T之间的距离应等于刀具球头部分的半径R,可求得交点Q(xq,yq,zq)的坐标:
(6)
比较内超环面齿轮齿面离散数据点坐标zG和干涉检验线与截平面的交点坐标zQ的大小,如果zG≥zQ,则刀具扫掠体在此位置不会发生局部干涉;如果zG 3.3 全局干涉检验 如图5所示,干涉检验面与刀具轴线和内超环面齿轮齿面相交,即干涉检验面方程为 z=zG (7) 图5 全局干涉检验Fig.5 Global interference detection 设干涉检验面与刀具轴线的交点为H(xH,yH,zH),与内超环面齿轮齿面相交得到若干个离散数据点。计算交点H到齿面离散数据点的最短距离,即 (8) xH=xTyH=yT 当该距离小于刀具半径时,即可判断此处会发生全局干涉。 根据内超环面齿轮离散建模方法,采用51个干涉检验面与内超环面齿轮齿面10条接触线求交,来提取内超环面齿轮齿面离散数据点,如图6所示。 图6 内超环面齿轮齿面离散数据点Fig.6 Stationary internal toroidal gear tooth surface discrete data points 根据内超环面齿轮齿面加工干涉检验方法,当刀具半径R取不同值时,内超环面齿轮齿面局部和全局干涉区域发生了变化,如图7和图8所示。随着刀具半径的减小,内超环面齿轮齿面的局部和全局干涉区域也相应减小。 为了验证本文方法能有效地避免内超环面齿轮齿面加工时出现的干涉现象,对内超环面齿轮单齿进行了数控加工,如图9所示,当选取刀具半径R=5 mm时,基本不会出现干涉现象。 (a)R=8.0 mm (b)R=7.5 mm (c)R=7.0 mm (d)R=6.5 mm图7 内超环面齿轮齿面局部干涉区域Fig.7 Stationary internal toroidal gear tooth surface local interference area (a)R=8.0 mm (b)R=7.0 mm (c)R=6.0 mm (d)R=5.0 mm图8 内超环面齿轮齿面全局干涉区域Fig.8 Stationary internal toroidal gear tooth surface global interference area 图9 内超环面齿轮单齿数控加工实物图Fig.9 Stationary internal toroidal gear single tooth surface material object 本文引入干涉检验面簇与内超环面齿轮齿面接触线簇求交,提取齿面离散数据点,将内超环面齿轮齿面离散化,并以内超环面齿轮齿面离散数据点为依据,构造干涉检验线簇,运用截平面将刀具扫掠体离散化。通过求解截平面处刀具中心坐标,比较内超环面齿轮齿面离散数据点和干涉检验线与截平面交点的z坐标来确定局部干涉区域;通过干涉检验面与刀具轴线的交点到齿面离散数据点的最短距离和刀具半径之间的比较来确定全局干涉区域。通过实例分析确定了内超环面齿轮齿面局部和全局干涉区域,选取不同的刀具半径局部和全局干涉区域的变化情况。可以看出,随着刀具半径的减小,内超环面齿轮齿面的局部和全局干涉区域也相应减小。运用本文的干涉检验离散建模方法,避免了加工干涉,并在Marzak数控加工中心上进行了内超环面齿轮的铣削加工,实际加工结果验证了本文方法的有效性。 [1] 洪玫, 姚立纲.超环面行星蜗杆传动系统研究进展与展望[J].机械传动,2013,37(6):129-132. HONG Mei, YAO Ligang. Study Current State and Prospect of the Toroidal Planet Worm Drive System[J]. Mechanical Transmission,2013,37(6):129-132. [2] DING X M, FUH J, LEE K S. Interference Detection for 3-axis Mold Machining[J].Computer-aided Design, 2001,33(8):561-569. [3] 李艳霞, 李科艳.基于数控仿真的刀具干涉验证算法研究[J].制造技术与机床,2010(8):28-31. LI Yanxia, LI Keyan. Research on Tool Interference Verification Algorithm Based on NC Simulation[J]. Manufacturing Technology & Machine Tool,2010(8):28-31. [4] DING S, MANNAN M A, POO A N.Oriented Bounding Box and Octree Based Global Interference Detection in 5-axis Machining of Free-form Surfaces[J]. Computer-aided Design,2004,36(13):1281-1294. [5] 曾志迎, 贾育秦, 袁金鹏, 等. 复杂曲面的五轴加工无干涉刀具路径生成技术研究[J]. 组合机床与自动化加工技术,2012(10):5-9. ZENG Zhiying, JIA Yuqin, YUAN Jinpeng, et al. Research on Gauging-free Cutter Path Generation Technology of Complex Surfaces[J]. Modular Machine Tool & Automatic Manufacturing Technique,2012(10):5-9. [6] 李万军,赵东标,牛敏,等.五轴加工全局干涉检查及其避免[J].计算机集成制造系统,2011,17(5):1011-1015. LI Wanjun, ZHAO Dongbiao, NIU Min, et al. Global Tool Interference Check and Avoidance in Five-axis Numerical Control Machining[J]. Computer Integrated Manufacturing Systems,2011,17(5):1011-1015. [7] 杜娟, 闫献国, 田锡天. 复杂曲面五轴加工局部干涉处理技术研究[J].图学学报,2012,33(1):113-120. DU Juan, YAN Xianguo, TIAN Xitian. Local Interference Detection and Avoidance in Five-axis Machining of Complex Surfaces[J]. Journal of Graphics,2012,33(1):113-120. [8] 王国勋, 舒启林, 王军, 等. 复杂曲面五轴加工干涉检查的研究[J].中国机械工程,2014,25(3):299-303. WANG Guoxun, SHU Qilin, WANG Jun, et al. Tool Interference Checking for Five Axis NC Machining of Sculptured Surfaces[J]. China Mechanical Engineering,2014,25(3):299-303. [9] CAN A, UNUVAR A. A Novel Iso-scallop Tool-path Generation for Efficient Five-axis Machining of Free-form Surfaces[J]. International Journal of Advanced Manufacturing Technology,2010,51(9/12):1083-1098. [10] MAKHANOV S S. Adaptable Geometric Patterns for Five-axis Machining: a Survey[J]. International Journal of Advanced Manufacturing Technology,2010,47(9/12):1167-1208. [11] JUN C S, CHA K, LEE Y S. Optimizing Tool Orientations for 5-axis Machining by Configuration-space Search Method[J]. Computer-aided Design,2003,35(6):549-566. [12] RAO A, SARMA R. On Local Gouging in Five-axis Sculptured Surface Machining Using Flat-end Tools[J]. Computer-aided Design,2000,32(7):409-420. [13] 洪玫, 姚立纲. 基于数值方法的内超环面齿轮齿廓离散建模[J].图学学报,2013,34(4):88-93. HONG Mei, YAO Ligang.Discrete Modeling of the Tooth Profile of the Stationary Internal Toroidal Based on Numerical Method[J]. Journal of Graphics,2013,34(4):88-93. [14] 洪玫.超环面行星蜗杆传动齿廓几何建模与基于误差和弹性变形的啮合特性分析[D].福州:福州大学,2014. HONG Mei. Tooth Profile Geometry Modeling and Meshing Characterictic Analysis Based on the Errors and Elastic Deformation for the Toroidal Drive[D]. Fuzhou: Fuzhou University,2014. (编辑 陈 勇) Interference Detection Method on Stationary Internal Toroidal Gear Based on Discrete Model HONG Mei YAO Ligang School of Mechanical Engineering and Automation,Fuzhou University,Fuzhou,350116 An interference detection method was put forward to effectively solve the problems of machining local and global interference phenomenons on stationary internal toroidal gear tooth surfaces. The introduction to interference detection plan clusters and the structure of interference detection line clusters were to obtain stationary internal toroidal gear tooth surface and tool scanning body discretization model. By using stationary internal toroidal gear tooth surface and tool scanning body discretization model, and through solving the cutting plane tool centers, stationary internal toroidal gear tooth surface machining local and global interference areas were determined. And through the example analyses, the feasibility of machining interference detection method of stationary internal toroidal gear tooth surface was further verified. toroidal drive;stationary internal toroidal gear;complex surface;interference detection; discrete modeling 2017-04-01 国家自然科学基金资助项目(50675035);福建省自然科学基金资助项目(2016J05120);福建省教育厅资助项目(JAT160065) TH132 10.3969/j.issn.1004-132X.2017.15.004 洪 玫,女,1980年生。福州大学机械工程及自动化学院讲师、博士。主要研究方向为数字化设计与制造。发表论文8篇。E-mail:8741513@qq.com。姚立纲,男,1964年生。福州大学机械工程及自动化学院教授、博士。
4 实例分析
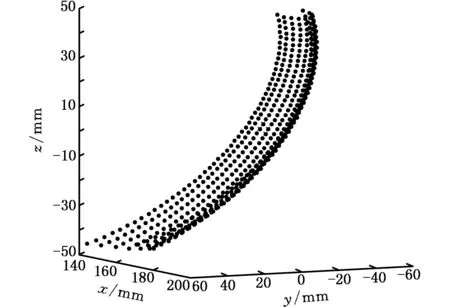
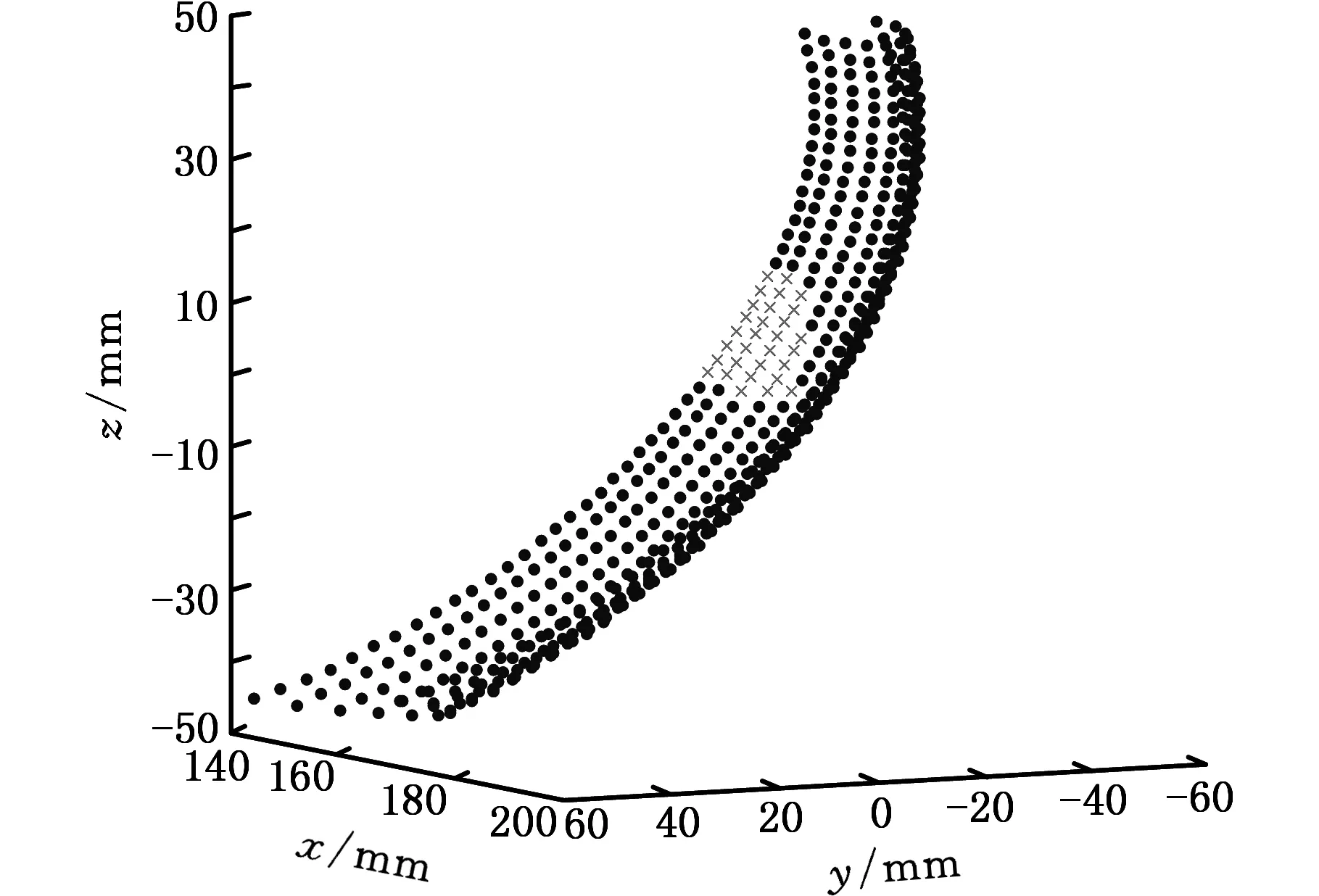



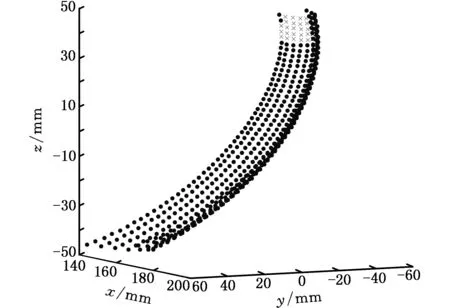



5 结语

