三瓣式气体箔片径向轴承的静动态特性

冯 凯 胡小强 赵雪源 李文俊

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

三瓣式气体箔片径向轴承的静动态特性

冯 凯 胡小强 赵雪源 李文俊

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

针对一种新型三瓣式气体箔片轴承，考虑接触界面库仑摩擦后提出了相应的刚度计算模型，并通过求解动压气体润滑Reynolds方程，计算并分析了轴承的静态特性和动态特性。研究了转速、载荷、轴承预载和轴承安装角对该轴承静动态特性的影响。静态特性方面，轴承预载可以较大程度地提高承载能力，且高转速下承载能力更强；安装角度对承载能力的影响呈正/余弦规律变化，且随着转速增大，最大承载能力所对应的安装角不断减小，并最终稳定在70°。动态方面，轴承动态直接刚度随预载增大而显著增大，阻尼变化较小；轴承动态刚度和阻尼随安装角的变化也表现为正/余弦规律，且随安装角的增大，两直接刚度和两直接阻尼分别呈异步变化趋势。

气体箔片轴承; 静态特性; 动态特性；轴承预载；安装角

0 引言

气体箔片轴承以其高速、无油、耐高温和效率高等显著优点在航空航天及民用等领域获得了广泛运用，如飞机上的空气循环机(air cycle machine)[1-2]、涡轮交流发电机[3]、涡轮增压器[4-5]等。早在1972年，AiResearch公司(后更名为Honeywell)为美国国家航空航天局(NASA)设计制作了一款由气体箔片轴承支承、额定功率为125 kW的TAC(turbo-alternator-compressor)，其工作状态良好[6]；1974年，美国海军第一次将气体箔片轴承应用于A7E战机的空体循环机上，并在越南战争中投入使用，因气体箔片轴承较球轴承更为可靠的表现，该轴承在美国海军飞机中获得了大量推广[7]。除此之外，微型轴承也是一项研究热点。SALEHI等[8]设计搭建了由空气箔片轴承支撑、模拟微型燃气轮机的70万转转子实验台；张海军等[9]研究了微气体轴承-转子系统的动力学特性。

气体箔片轴承的种类在不断增加，各类轴承性能差异也较大。为了系统地分析不同箔片轴承的特点，KIM[10]对比了四种轴承的静动态特性：第一种为普通整圆型波箔轴承；第二种为整圆型波箔轴承，且其轴向刚度抛物线变化；第三种为三瓣式波箔轴承，周向等刚度；第四种为三瓣式波箔轴承，且其周向刚度抛物线变化。除此之外，DELLACORTE等[11]提出了一种轴承承载能力的计算公式，并根据各种轴承的承载能力，将现有径向箔片轴承分成三代：第一代在轴向和周向上都保持等刚度；第二代在轴向和周向中某单一方向上保持变刚度；第三代在轴向和周向上都保持变刚度，有的轴承甚至在径向上也是变刚度。

本文研究了一种第三代气体箔片轴承，该轴承具有三瓣式弹性支承箔片和对应的三瓣式顶层箔片。针对该类型轴承，Capstone公司联合MOORE等[12]设计了一个实验台来测量此轴承的动态特性参数。另外，Capstone公司也联合KIM等[13]对该轴承进行了建模分析，并将理论计算得到的参数与实验数据进行了对比。但由于在模型简化时，弹性支承箔片刚度模型忽略了接触界面库仑摩擦，将刚度视为定值，故未能很好地反映刚度情况。

为了建立对于箔片轴承较为准确、合理的刚度模型，研究人员付出了极大努力。HESHMAT等[14]针对波箔式轴承提出了一种用柔性系数来计算箔片刚度的方法；FENG等[15]针对鼓泡型轴承(multi wound foil bearing)提出了相应的计算模型，并在考虑箔片局部变形影响情况下，对轴承静态性能进行了预测；LEZ等[16]针对波箔式轴承，考虑接触界面库仑摩擦，提出一种较为复杂的八弹簧模型，并且在此模型基础上，对轴承进行了非线性分析[17]；FENG等[18]针对波箔式轴承，提出了一种杆簧模型，并基于该模型研究了轴承的静态特性和非线性特性[19]、动态特性[20]以及热动力学特性[21]；FENG等[22]针对一种新型弹簧箔片轴承，提出了分析模型，并设计了实验来进行模型验证。

本文根据轴承的结构特点，考虑接触界面库仑摩擦，提出了一种刚度随变形量变化的计算模型，通过二维刚度形式体现了轴承的变刚度性质，并研究了该轴承的静动态特性。

1 轴承结构及刚度模型

1.1 轴承结构

本文所研究的三瓣式气体箔片轴承的结构如图1所示。 该轴承主要由轴承套、三瓣弹性支承箔片和三瓣顶层箔片组成。轴承套内壁有三个均匀分布的燕尾槽，用于固定弹性支承箔片和顶层箔片。内壁上由三个燕尾槽分隔开的三段圆弧与轴承外壁并非同心，而是具有3.65 mm的偏心距。图1中显示了其中一瓣弹性支承箔片和相对应顶层箔片的安装方法，另外两对箔片的安装与此类似。顶层箔片和轴承套在结构上存在一定预载，参照图2，预载rp指的是顶层箔片圆心OT到轴承中心OB的距离d与轴承名义间隙C的比值，即rp=d/C。另外，由于轴承预载的存在，此时轴承名义间隙C的定义也较为特殊：当转子处于轴承中心位置时，3个燕尾槽确定的圆与转子外壁的间隙称为名义间隙；三个顶层箔片的内接包络圆直径定义为轴承直径，图2中，R为轴承半径；θa为轴承安装角，即左上方燕尾槽与垂直方向的夹角；θ0为偏位角，即转子中心与轴承中心连线与x轴正方向的夹角;OR为转子中心；e为转子偏心距。

图1 三瓣式气体箔片轴承Fig.1 Three-pad gas foil journal bearing

图2 轴承简图和坐标系Fig.2 Schematic view of bearing and coordinate system

该轴承具有变刚度特性，其主要原因在于弹性支承箔片的特殊结构形式。弹性支承箔片由8排弹性小片和连接它们的细梁组成，每个弹性小片都是一个变截面对称梁，相邻两排的弹性小片结构尺寸不同，且交错分布；在轴向上，弹性小片的整体尺寸呈先增大、后减小的趋势；沿转子转动方向，弹性小片整体尺寸逐渐增大，刚度也不断增大，所以沿转子转动方向，箔片前端比后端更易变形，在前端形成较厚气膜，在后端形成较薄气膜，构成楔形效应。这种变刚度结构形式可以有效地提高轴承的稳定性和承载能力[12]。本文分析所用轴承的主要参数见表1。

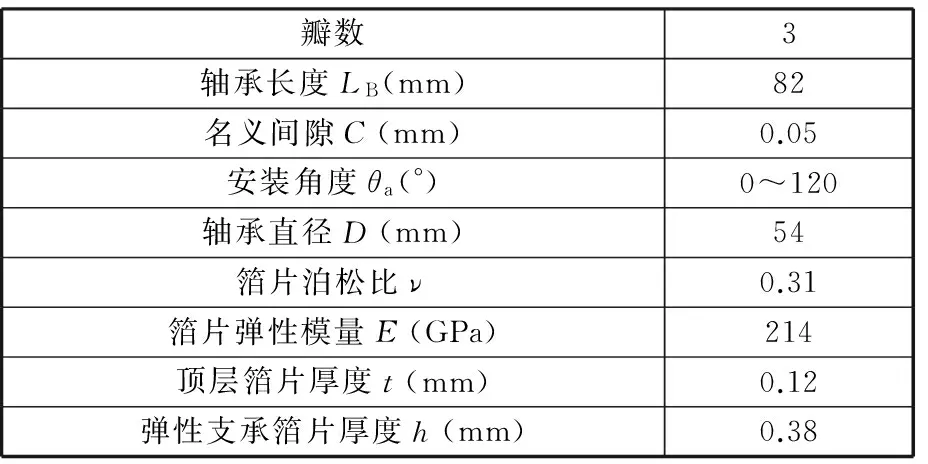
表1 轴承主要参数

1.2 弹性支承箔片刚度模型

为了便于理解和方便分析计算，将轴承结构沿圆周方向展开到平面，如图3所示。分析弹性支承箔片上一个弹性小片，所得坐标转换关系为

(1)

式中，ξx、ξy分别为展开后的横坐标和纵坐标；φ为轴承柱坐标中的角度；R1为轴承套内表面半径；L1为轴承套内表面圆心到弹性小片中点的距离。

图3 轴承等效展开图Fig.3 Equivalent expansion along the circumference direction

经计算对比发现，将轴承结构沿圆周方向展开后，弹性小片的等效形状接近圆弧，且将其简化为经过弹性小片两端点和中点的圆弧时，误差小于0.035%，因此，将等效后的弹性小片结构作为圆弧处理。

等效弹性小片结构呈圆弧拱形，两端支脚直接与轴承套接触，存在明显的库仑摩擦。将弹性小片结构简化为两根相互铰接刚性杆和一根水平弹簧的形式，如图4所示。

图4 弹性支承箔片刚度模型Fig.4 Model of the support foil

根据弹性小片的结构尺寸，并运用能量法来求解杆簧模型的水平刚度K1。详细求解过程如下。

变形能量方程为

(2)

D=Ehp3/[12(1-ν2)]

式中,M为截面上弯矩；N为截面上轴力；A为截面面积;hp为截面厚度；L为截面宽度。

由图5可得

(3)

式中，F1、F2分别为两端点所受力；Rb为等效圆弧半径；θf为圆弧拱形半弧角度；ψ为圆弧上任一点与右端点夹角。

图5 水平刚度K1的求解Fig.5 Analysis of horizontal stiffness K1

由于弹性支承箔片上所有弹性小片均为变截面结构，故任取一弹性小片，如图6所示，其截面形状按图上规律变化，其中，a0、a1为常数。

图6 弹性小片结构Fig.6 Elastic piece

弯曲变形能量

(4)

将式(3)和图6中的变化规律代入式(4)：

(5)

另外，纵向变形能量

(6)

代入式(3)和图6中的变化规律后，有

(7)

水平变形量

(8)

所以得到水平弹簧刚度：

(9)

事实上，弹性小片的水平位移与垂直变形存在对应关系，所以上述模型最终可以被等效为刚度是Kv的垂直弹簧。弹性小片两端自由，且与轴承套之间的摩擦因数μ为0.2，自由端的受力分析如图7所示。其中，Fp为弹性小片所受压力；Ff为端点所受摩擦力；Fk为等效水平弹簧力；Fbeam为等效刚性杆的水平分力；FR为等效刚性杆的垂直分力；α为等效刚性杆的水平夹角。

图7 自由端受力分析图Fig.7 Force analysis at the free end

根据端点位置受力分析，得平衡方程：

Fbeam=Ff+Fk

(10)

FR=Fp/2Fbeam=FR/tanα

Ff=μFRFk=2K1ΔL

Fp=KvΔh

式中，Δh为中点垂直变形量；ΔL为弹性小片一端水平位移。

将上述各式代入式(10)得

(11)

ΔL=

由式(11)可以看出，垂直刚度是关于垂直变形量Δh的函数，所以箔片在径向上具有变刚度趋势。

因该类轴承的研究工作正处于前期阶段，在轴承性能预测之前，需要进行适当的简化。本文将轴向上各弹性小片的结构尺寸视为相同，并且后续的计算和分析都是基于该简化前提进行的。

1.3 顶层箔片刚度模型

顶层箔片是由24自由度的壳单元有限元模型来描述的[18]，并且按弹性支承箔片相同的单元划分规则得到同等数量单元。通过计算得到顶层箔片节点上的垂直刚度矩阵Ktop，与1.2节计算得到的弹性支承箔片节点上的刚度矩阵Kv进行叠加耦合，最终得到箔片全局刚度矩阵：Kglob=Ktop+Kv。由箔片结构形式可知，顶层箔片变形量矩阵δ的计算是基于全局刚度得到的，即F=Kglobδ，其中，F为节点力矩阵。

2 静态特性预测

2.1 静态特性计算

箔片轴承内气膜压力分布是通过求解恒温下气体Reynolds方程得到的。视气体为理想可压缩流体，根据图2所示的坐标定义，Reynolds方程可以写成以下形式：

(12)

在轴承实际工作时，考虑轴承名义间隙、偏心率、预载和箔片变形后，量纲一气膜厚度

(13)

式中，ε为偏心率，ε=e/C；θp为每瓣中心位置对应的角度；δ(θ,z)为顶层箔片变形量。

由于三瓣式箔片轴承的每瓣上气膜压力和气膜厚度的处理较为独立，故通过对每一瓣参数进行单独求解、最后整体组装的方式来计算该轴承的静态特性。对每瓣进行求解时，由于轴向两端直接与周围大气接触，气膜压力等于大气压；另外，任意两瓣过渡处气膜厚度较大，压力接近于大气压，故静态计算的边界条件设为：

式中，θs为每瓣开始的位置。

目前，大多数箔片轴承的静态和动态预测都是在一维刚度简化的基础上进行的，即在轴向上认为箔片刚度不变，用圆周方向的一组刚度来表示箔片刚度特征[10，14]。当然，对于箔片刚度在轴向没有变化的情况，一维刚度简化下的预测结果可信度还是比较好的，但对于本文所分析的轴承，其刚度在轴向上是交错分布的，如果使用一维刚度进行简化，则与实际情况存在较大差异，不能很好地预测轴承性能，所以本文使用二维刚度，从而可更准确地表示弹性支承箔片的刚度分布。

性能预测的数值计算方案如下：

(3)根据顶层箔片刚度模型计算出Ktop，根据弹性支承箔片刚度模型和顶层箔片变形量计算出Kv，最终得到箔片全局刚度Kglob。

(4)根据新的气膜压力分布和箔片全局刚度，计算得到新的顶层箔片变形量δ1(θ,z)。

(5)如果新的气膜压力和新的顶层箔片变形量相比之前值的变化量都小于0.0001，则跳出循环，否则回到步骤(2)继续计算。

在计算收敛之后，根据轴承的气膜压力分布即可算出轴承所承受的静态载荷，因此，该转速下偏心率和载荷得以对应。

转速为40 kr/min，轴承载荷为20 N，θa=0°，rp=0.3时(轴承其他参数见表1)，某一瓣弹性支承箔片的刚度计算结果如图8所示。可以明显看出：弹性支承箔片刚度沿圆周方向呈单调增大趋势。

图8 箔片刚度分布示意图Fig.8 Structural rigidity distribution

图9为在转速为40 kr/min，安装角θa=0°，rp=0.3，给定轴承载荷为20 N时的气膜厚度分布图和气膜压力分布图。由于预载的存在，在气膜厚度分布图和压力分布图中出现了三个明显的波谷和波峰，且压力最大值出现在气膜厚度最小处附近，位于第二瓣上。另外可以发现，气膜厚度图上出现了较多尖角毛刺，这是顶层箔片局部变形所造成的。

(a)气膜厚度分布图

(b)气压分布图图9 轴承气压分布和气膜厚度分布(40 kr/min，20 N)Fig.9 Film thickness and pressure distribution (40 kr/min，20 N)

图10 最小气膜厚度与载荷关系曲线Fig.10 Minimum thickness versus bearing load

由图10可以看出，随着载荷的增大，两种轴承的最小气膜厚度都呈线性减小趋势；对于相同转速和载荷，三瓣式轴承的最小气膜厚度小于刚性轴承的最小气膜厚度；相比之下，随着载荷增大，三瓣式轴承最小气膜厚度减小的速度更快；另外，在同一轴承载荷下增大转速，两种轴承的最小气膜厚度都会增大。

图11 轴心稳定位置与载荷关系曲线Fig.11 Rotor stable position versus bearing load

由图11可以看出，在相同载荷下，两种轴承高转速的偏心率均小于低转速的偏心率，这是因为提高转速，增大了气膜压力，推动转子朝轴承中心位置移动；在同一转速和相同载荷变化范围下，三瓣式轴承对应的偏心率变化范围远大于刚性轴承的偏心率变化范围，并且载荷增大时，刚性轴承的偏心率增大速度逐渐减缓，而三瓣式轴承的偏心率几乎保持恒定速率增大；另外一个比较特殊的现象是：随着载荷增大，刚性轴承的偏位角保持逐渐减小趋势，而三瓣式轴承的偏位角是先减小，偏心率在0.27左右时，偏位角逐渐增大，当偏心率达0.33左右时，偏位角又开始减小，这是因为当偏心率增大到一定程度，转子位于两瓣箔片之间，且靠近燕尾槽，气压发生变化，此时转子稳定位置会发生一定波动。除此之外，还可以发现在相同条件下，刚性轴承的偏位角大于三瓣式轴承的偏位角，这是因为三瓣式轴承的切向力比刚性轴的切向力小，所以三瓣式轴承的偏位角相对更小[23]。

2.2 轴承预载对静态性能的影响

由式(5)可知，轴承预载直接影响气膜厚度，进而影响轴承静态特性。为了研究轴承预载与静态特性的关系，在给定F=20 N，θa=0°，转速分别为25 kr/min和40 kr/min的情况下，偏心率与轴承预载的关系曲线如图12所示。由图12可知，在一定转速下，增大轴承预载，偏心率将随之减小，说明轴承的承载能力得到了提升，其中rp=0相当于顶层箔片与轴承套同心的情况，所以同心形式的轴承承载能力相对更小，偏心率的减小速度随着预载增加而不断降低；在一定轴承预载下，随转速的增大，偏心率减小，且随预载的增大，不同转速偏心率的差值逐渐减小。

图12 偏心率与轴承预载关系曲线Fig.12 Eccentricity ratio versus preload

2.3 安装角度对静态性能的影响

需要强调的是，以上所有的静态预测结果都是在安装角θa=0°的前提下得到的，但是当安装角θa不同时，整个轴承的气膜分布情况将发生较大变化，在一定程度上影响轴承的整体性能。

为了找到最佳静态性能对应的安装角，指导试验和工程应用，本文以承载能力为评价指标，分析了在给定F=20 N，rp=0.3时，转速分别为15 kr/min、25 kr/min、30 kr/min、40 kr/min、45 kr/min和50 kr/min的情况下，偏心率随安装角度的变化关系，如图13所示。由图13可知，偏心率随着安装角度的增大呈正/余弦曲线的变化规律。因为轴承载荷固定，所以在相同转速下，最小偏心率位置可以认为是轴承承载能力最大的状态，称之为最佳安装角。随着转速的增大，轴承最佳安装角逐渐减小，并最终稳定于70°。另外可以明显发现，随着转速增大，偏心率的变化幅值也在不断降低。

图13 偏心率与安装角度关系曲线Fig.13 Eccentricity ratio versus installation angle

3 动态特性预测

3.1 动态特性计算

轴承动态参数预测是在静态稳定状态下，给予微小径向扰动得到的[24-26]。微小扰动下气体Reynolds方程为

(14)

式中，υ为激振频率，本文研究γ=1时的情况。

忽略高阶小量后，气膜压力、气膜厚度和箔片变形量的泰勒展开式(所有参数均为量纲一的值)可分别表示为

(15)

(16)

(17)

将式(15)～式(17)代入式(14)后，通过对各分项进行分离[25]，分别得到轴承动态刚度系数和动态阻尼系数：

(18)

(19)

式中，Kxx、Kyy为直接刚度；Kxy、Kyx为交叉刚度；Cxx、Cyy为直接阻尼；Cxy、Cyx为交叉阻尼。

式(18)、式(19)中用Kij统一表示动态刚度，指的是j方向的力与其所引起的i方向位移的比值；用Cij统一表示动态阻尼，指的是j方向的力与其所引起的i方向速度的比值。

图14所示为预载rp=0.3、载荷F=20 N时，使用微扰动法计算得到的轴承动态刚度和动态阻尼随转速的变化情况。

(a)动态刚度与转速关系曲线

(b)动态阻尼与转速关系曲线图14 轴承动态刚度和动态阻尼随转速的变化情况Fig.14 Dynamic stiffness and damping versus rotor speed

由图14a可以看出，直接刚度Kxx和Kyy近似相等，且都随着转速增大而增大；交叉刚度明显小于直接刚度；交叉刚度Kxy随转速的增大而减小，Kyx随转速的增大而增大；转速增大后，交叉刚度的绝对值趋向于0，所以轴承稳定性不断提高。

由图14b可以看出，直接阻尼Cxx和Cyy近似相等，且都随着转速的增大而减小。在计算范围内，直接阻尼大于交叉阻尼，但它们的差值随着转速的增大而逐渐减小；Cxy随着转速的增大而增大，Cyx随着转速的增大而减小。

3.2 轴承预载对动态性能的影响

图15所示为F=20 N、θa=0°时，分别在25 kr/min和40 kr/min两种转速下，轴承预载对动态刚度和动态阻尼的影响。由图15a可知，对于同一转速下，随着轴承预载的增大，直接动态刚度Kxx和Kyy都显著增大，且Kxx≈Kyy、rp=0的同心形式轴承的刚度最小；由图15b可知，对于相同转速，增大轴承预载，直接阻尼Cxx和Cyy变化较小。另外，可以发现转速为25 kr/min时，Kyy与Cyy在rp=0.2附近都出现了突变情况，在文献[27]中也出现了类似情况。

(a)直接刚度与轴承预载关系曲线

(b)直接阻尼与轴承预载关系曲线图15 预载对轴承动态刚度和动态阻尼的影响Fig.15 Dynamic stiffness and damping versus preload

3.3 安装角度对动态性能的影响

(a)动态刚度与安装角度关系曲线

(b)阻尼与安装角度关系曲线图16 安装角度对动态刚度和动态阻尼的影响Fig.16 Dynamic stiffness and damping versus installation angle

图16所示为F=20 N，rp=0.3时，在40 kr/min转速下，轴承安装角对动态刚度和动态阻尼的影响。可以明显看出，动态刚度和阻尼随安装角度的变化都呈正/余弦规律。由图16a可知，直接刚度Kxx和Kyy呈异步变化趋势，相位相差180°，Kxx在安装角为90°左右取得最大值，而Kyy在安装角为30°附近取最大值；直接刚度和交叉刚度的变化幅值几乎相等，且交叉刚度远小于直接刚度。由图16b可知，直接阻尼Cxx和Cyy也呈相位角相差180°的异步变化趋势，并且Cxx在安装角为110°附近取得最大值，Cyy在安装角为50°附近取得最大值；直接阻尼和交叉阻尼的变化幅值也相差不大。

4 结论

(1)三瓣式箔片轴承的静态特性如下：当增大转速时，最小气膜厚度增大，偏心率减小；在相同转速下，逐渐增大载荷时，偏心率几乎以恒定速率增大，而偏位角则先减小后增大，到达特定位置后又开始减小。

(2)该轴承的动态特性如下：随着转速增大，直接刚度Kxx和Kyy几乎相等，且不断增大；交叉刚度Kxy和Kyx近似对称，且小于直接刚度；轴承直接阻尼Cxx和Cyy也几乎相等，且都随转速增大而减小；交叉刚度Cxy和Cyx的绝对值都随转速增大而减小。

(3)在相同情况下，增大轴承预载，将使偏心率减小，轴承承载能力提高；随着轴承预载的增大，直接动态刚度将得到较大提升，而直接动态阻尼则变化较小。

(4)安装角度对轴承静态和动态特性的影响都是以正弦/余弦形式表现的。在特定工况下，总存在最佳安装角来实现最大承载能力；随转速增大，最佳安装角不断减小，当转速在40 kr/min以上时，最佳安装角稳定在70°左右，该结果对工程应用有一定指导意义。随安装角的增大，两直接刚度异步变化，两直接阻尼也呈异步变化趋势，根据设计要求综合考虑后，可得到最理想安装角度。

[1] EMERSON T P. Application of Foil Air Bearing Turbomachinery in Aircraft Environmental Control Systems[J].Control Systems,1978,100(11):111-111.

[2] DELLACORTE C, RADIL K C, BRUCKNER R J, et al. Design, Fabrication and Performance of Open Source Generation Ⅰ and Ⅱ Compliant Hydrodynamic Gas Foil Bearings[J]. Tribology Transactions,2008,51(3):254-264.

[3] JEONG S, KIM E J, LEE Y B. Rotordynamic Behavior of ORC Micro Turbine Generator Supported by Gas Foil Bearings[C]//13th Asian International Conference on Fluid Machinery. Tokyo,2015:AICFM13-129(1-9).

[4] FENG K, LI W J, CHENG M M. A Simulator Test-bed for High-speed Oil-free Turbine Engine Rotor Dynamics[C]// Yunlin: CTTT,2015:87-88.

[5] AGRAWAL G L. Foil Gas Bearings for Turbomachinery, SAE Paper No. 901236[R]. Williamsburg: SAE,1990.

[6] AiResearch Mfg. Co.. Preliminary Design of a Mini-Brayton Compressor-Alternator-Turbine (CAT)[EB/OL]. [2016-06-20]. http://ntrs.nasa.gov/.

[7] AGRAWAL G L.Foil Air/Gas Bearing Technology—an Overview[C]//International Gas Turbine and Aeroengine Congress and Exhibition.New York,1997: V001T04A6-VT04A6.

[8] SALEHI M, HESHMAT H, WALTON J F, et al. Operation of a Mesoscopic Gas Turbine Simulator at Speeds in Excess of 700,000 rpm on Foil Bearings[J].Journal of Engineering for Gas Turbines & Power, 2007,129(1):87-94.

[9] 张海军, 祝长生. 微气体轴承-转子系统动力特性研究[J]. 中国机械工程, 2012,23(12):1400-1403. ZHANG Haijun, ZHU Changsheng. Study on Dynamics of Micro Gas Journal Bearing-rotor System[J]. China Mechanical Engineering,2012,23(12):1400-1403.

[10] KIM D. Parametric Studies on Static and Dynamic Performance of Air Foil Bearings with Different Top Foil Geometries and Bump Stiffness Distributions[J]. Journal of Tribology, 2007,129(2):354-364.

[11] DELLACORTE C, VALCO M J. Load Capacity Estimation of Foil Air Journal Bearings for Oil-free Turbomachinery Applications[J]. Tribology Transactions,2000,43(4):795-801.

[12] MOORE J J, LERCHE A, ALLISON T, et al. Development of a High Speed Gas Bearing Test Rig to Measure Rotordynamic Force Coefficients[J]. Journal of Engineering for Gas Turbines and Power,2010,133(10):541-548.

[13] KIM T, ANDRES L S, NOURSE J, et al. Modeling of a Gas Foil Bearing for Microturbine Applications: Predictions Versus Experimental Stiffness and Damping Force Coefficients[C]// World Tribology Congress. Kyoto,2009:6-11.

[14] HESHMAT H, WALOWIT J A, PINKUS O. Analysis of Gas-lubricated Foil Journal Bearings[J]. Journal of Lubrication Technology, 1983,105(4):647-655.

[15] FENG K, KANEKO S. A Numerical Calculation Model of Multiwound Foil Bearing with the Effect of Foil Local Deformation[J]. Journal of System Design and Dynamics, 2007,1(3):648-659.

[16] LEZ S L, ARGHIR M, FRENE J. A New Bump-type Foil Bearing Structure Analytical Model[J].Journal of Engineering for Gas Turbines and Power,2007,129(4):747-757.

[17] LEZ S L, ARGHIR M, FRENE J. Nonlinear Numerical Prediction of Gas Foil Bearing Stability and Unbalanced Response[J]. Journal of Engineering for Gas Turbines & Power,2009,131(1):1089-1100.

[18] FENG K, KANEKO S. Analytical Model of Bump-type Foil Bearings Using a Link-spring Structure and a Finite-element Shell Model[J]. Journal of Tribology,2010,132(2):021706(1-11).

[19] FENG K, KANEKO S. Parametric Studies on Static Performance and Nonlinear Instability of Bump-type Foil Bearings[J]. Journal of System Design & Dynamics,2010,4(6):871-883.

[20] FENG K, KANEKO S. Prediction of Dynamic Coefficients of Bump-type Foil Bearings with Bumps Considered as Link-spring Structures[J]. Tribology Online,2011,6(1):10-18.

[21] FENG K, KANEKO S, HOUJOH H. Integrated Numerical Model for Thermohydrodynamic Analysis of Bump-type Foil Bearings[C]// International Design Engineering Technical Conferences and Computers and Information in Engineering Conference.New York,2011:3-14.

[22] FENG K, HU J, LIU W, et al. Structural Characterization of a Novel Gas Foil Bearing with Nested Compression Springs: Analytical Modeling and Experimental Measurement[J]. Journal of Engineering for Gas Turbines & Power,2016,138(1):012504(1-11).

[23] MUSZYNSKA A. Rotordynamics[M]. Boca Raton: CRC Press,2005:1-29.

[24] PENG J P, CARPINO M. Calculation of Stiffness and Damping Coefficients for Elastically Supported Gas Foil Bearings [J]. Journal of Tribology,1993,115(1):20-27.

[25] FENG K, KANEKO S. Calculation of Dynamic Coefficients for Multiwound Foil Bearings [J]. Journal of System Design and Dynamics,2009,3(5):841-852.

[26] 戚社苗, 耿海鹏, 虞烈. 动压气体轴承的动态刚度和动态阻尼系数 [J]. 机械工程学报,2007,43(5):91-98.QI Shemiao, GENG Haipeng,YU Lie. Dynamic Stiffness and Dynamic Damping Coefficients of Aerodynamic Bearings[J]. Journal of Mechanical Engineering,2007,43(5):91-98.

[27] 杨利花. 可倾瓦与弹性箔片动压气体轴承的性能研究[D]. 西安：西安交通大学,2009. YANG Lihua. Study on the Performance of Aerodynamic Tilting-pad and Compliant Foil Bearings[D].Xi’an: Xi’an Jiaotong University,2009.

(编辑 陈 勇)

Static and Dynamic Performances of a Three-pad Gas Foil Journal Bearing

FENG Kai HU Xiaoqiang ZHAO Xueyuan LI Wenjun

State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan University,Changsha, 410082

A novel three-pad gas foil bearing was analyzed herein. The stiffness was modeled by considering the Coulomb’s friction. The static and dynamic characteristics of the bearing were obtained by solving the Reynolds equation. The effects of rotor speed, load, pad preload and installation angle on the bearing performances were discussed. Static results indicate that the preload may increase the load capacity significantly especially at high rotor speed. The installation angle effecting on the load capacity is based on the law of sine/cosine rules. With the increasing of rotor speeds, the installation angle corresponding to the maximum load capacity decreases constantly, and stabilizes at 70° eventually. Dynamic results show that the direct stiffness increases significantly with the increasing of the pad preload. However, the damping only has slightly variation. The installation angle effecting on the stiffness and damping is also based on the law of sine/cosine rule. And two direct stiffnesses show the trend of asynchronization with the increasing of installation angles. Meanwhile, two direct dampings also vary asynchronously.

gas foil bearing; static performance; dynamic performance; preload; installation angle

2016-07-01

国家自然科学基金资助项目(51575170)；国家科技支撑计划资助项目(2015BAF32B01)

TH133.35

10.3969/j.issn.1004-132X.2017.15.010

冯 凯，男，1982年生。湖南大学机械与运载工程学院教授、博士研究生导师。主要研究方向为微型燃气轮机、涡轮增压器、高速空压机等。E-mail: kfeng@hnu.edu.cn。胡小强，男，1991年生。湖南大学机械与运载工程学院硕士研究生。赵雪源，男，1989年生。湖南大学机械与运载工程学院博士研究生。李文俊，男，1988年生。湖南大学机械与运载工程学院博士研究生。