一类非完整机械手的链式变换特性及其运动规划方法
李 亮 刘一方 谭跃刚
1.宝鸡文理学院机械工程学院,宝鸡,7210162.中国长江动力集团有限公司,武汉,4300703.武汉理工大学机电工程学院,武汉,430070
一类非完整机械手的链式变换特性及其运动规划方法
李 亮1刘一方2谭跃刚3
1.宝鸡文理学院机械工程学院,宝鸡,7210162.中国长江动力集团有限公司,武汉,4300703.武汉理工大学机电工程学院,武汉,430070
针对一类非完整三关节机械手提出了规避链式逆变换奇异位形的运动规划方法。根据非完整机械手的结构特点分离出广义坐标向量中的自由变量,将其边界值作为控制输入中的待定系数进行求解。对于非完整机械手在链式逆变换过程中出现的奇异性问题,提出令链式空间中一条轨迹向关节空间映射有解的不等式约束条件,利用增加附加位形约束的方法来规避非完整机械手的链式逆变换奇异位形。仿真与实验结果证明了运动规划算法的可行性与有效性。
非完整机械手; 链式变换; 奇异位形;运动规划
0 引言
机器人运动学方程中,对时间的导数不能积分为有限形式,这类约束称为非完整约束,含有非完整约束的系统称为非完整系统。虽然非完整约束限制了系统的瞬时运动,但在位形空间上是完全可控的,因此非完整系统具有更高的灵活性。此外,非完整系统的广义速度并不是相互独立的,故其控制输入数目少于广义坐标数目,呈现出欠驱动的特性,驱动装置的减少使得非完整系统具有结构紧凑、重量轻等特点。
非完整运动规划即在有限时间内使机器人系统从给定的初始位形运动到目标位形的控制输入求解问题[1]。非完整系统内部存在运动耦合,因此在机器人系统的位形空间内只有满足非完整约束的轨迹才是可行的。这一特性使得针对完整系统运动规划的纯几何方法都无法直接应用于非完整系统,故对非完整系统的运动规划显得更为复杂和困难。非完整系统的运动规划策略研究引起了国内外学者的广泛关注。
围绕链式系统路径规划的研究,主要集中在控制算法的设计和已有可链式化非完整系统的运动控制。MURRAY等[2]通过坐标及输入变换将轮式移动机器人的运动学方程转换成为一类结构简单的非完整系统——链式系统。TILBURY等[3]将三角函数、多项式、分段常数等含有待定系数的方程作为控制输入,实现了对链式系统的运动规划。LOOCK等[4]基于微分代数法研究轮式移动机器人,提出了具有平滑输出特征的路径规划方法。JANIAK等[5]利用牛顿下降法解决了能量最优条件下的路径规划问题。
虽然针对链式系统已有许多较成熟的运动规划算法,然而对非完整多关节机械手这类运动耦合度高、运动学模型复杂的非完整系统的运动规划并不容易[6]。由于非完整机械手的运动学模型与链式模型之间的映射在位形空间上并不完全微分同胚,在链式空间中规划所得的一条路径不能保证其能够完全映射至关节空间,即机械手某些关节在位形空间产生了模型变换奇异点或区间,如Nakamura非完整机械臂[7]、轮式拖挂车系统[8-9]等。尽管上述研究都已提到链式逆变换解的奇异性问题,但未深入讨论解决办法。本文以一类非完整三关节机械手为研究对象,利用惩罚函数和牛顿迭代法求解链式空间中一条链式逆变换有唯一解的轨迹。
1 非完整机械手的基本结构
非完整机械手以摩擦圆盘机构为运动传递单元,摩擦盘之间无滑动的滚动产生了不可积的速度约束,因此这类机械手系统为一阶非完整系统[10]。摩擦圆盘运动传递机构如图1所示,其中盘A为输入盘,盘B与盘D为输出盘。当盘A旋转时,通过滚动摩擦依次驱动盘B、C、D旋转。另外,当水平布置的摩擦盘B、盘D的中心轴转动时,各摩擦盘之间的运动传动比会产生变化,因此可以通过改变水平摩擦盘中心轴的角位移来控制摩擦盘之间的传动比。

图1 摩擦圆盘运动传递机构Fig.1 Friction disc motion transmission mechanism
在非完整机械手的每一个关节内布置一组摩擦圆盘机构,其中垂直布置的两圆盘与前一个关节固连,水平布置的两圆盘与后一个关节固连,非完整三关节机械手的机构模型如图2a所示,实物如图2b所示。其中,电机2驱动关节1转动,电机1驱动关节1的输入盘A1转动,摩擦圆盘机构中的一个输出盘B1通过齿轮传动机构驱动关节2中的输入圆盘A2转动,另一个输出盘D1通过同步带传动机构驱动关节2转动。关节2中的运动传递关系与关节1相同。
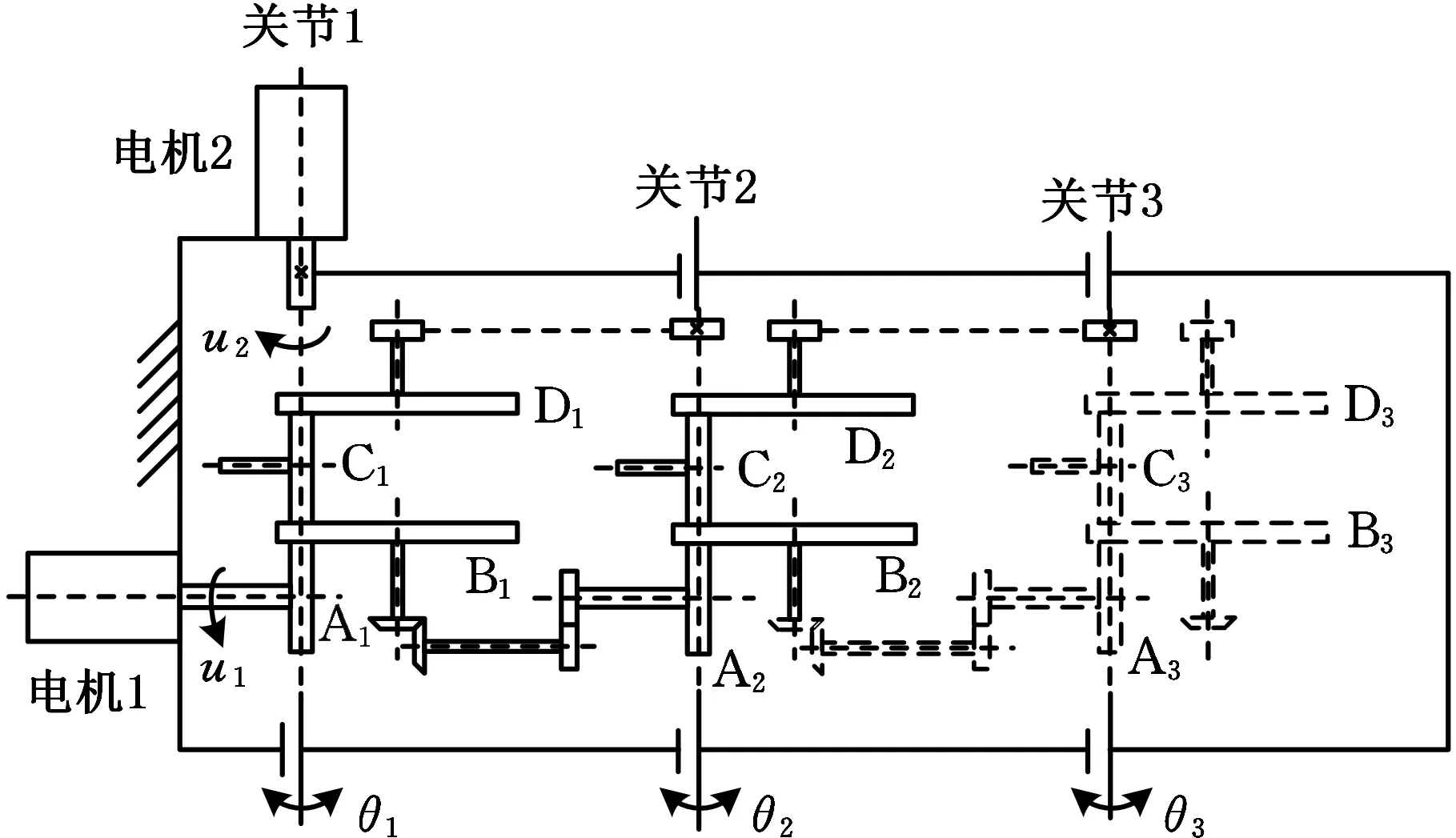
(a)非完整三关节机械手机构图

(b)非完整三关节机械手实物图图2 非完整三关节机械手Fig.2 Three-joint nonholonomic manipulator
非完整三关节机械手的位形空间由四个状态变量表示[11]:三个关节的转动角位移θ1、θ2、θ3以及一个输入盘的转动角位移φ1,而控制输入只有关节1的角速度与盘A1的角速度两个。这说明非完整机械手系统可以由少于广义坐标数目的控制输入来控制其运动。
摩擦盘间的运动为无滑动的滚动,因此相互接触的两摩擦盘在接触点处的相对速度为零。根据此运动关系可推导出非完整三关节机械手的运动学模型表达式:
(1)
式中,k2、k3为与结构尺寸有关的系数;μ1、μ2分别为盘A1和关节1的角速度。
2 非完整机械手的链式变换特性
2.1 链式变换
Sørdalen在研究多挂车系统的链式变换时,将其广义坐标向量选取为每个挂车牵引杆的转动角位移及最末一个挂车的位置坐标,得到一种符合三角形构造的非完整系统。这种三角形构造非完整系统的特点是其第i个广义速度只与i-1以后的广义坐标(含第i-1个)及输入有关。Sørdalen给出了符合三角形构造的无漂移仿射系统转换成为链式系统的条件及方法[8]。定理1 对于符合三角形构造的无漂移仿射系统:
(2)
i∈{3,4,…,n}qi-1=(qi-1,qi,…,qn)T

对于非完整三关节机械手,取其广义坐标向量q=(φ2,θ1,θ2,θ3)T,便可将非完整三关节机械手的运动学模型改写为如下所示的三角形构造形式:
(3)
式中,kg为与结构尺寸有关的系数。
根据定理1可以证明非完整三关节机械手系统可通过如下坐标变换:
(4)
转换成为两输入四维链式系统:
(5)
式中,v1和v2分别表示链式变量z1和z2的速度,由式(4)可知,v1是输入圆盘A2的角速度,v2没有明确的物理意义。
2.2 链式逆变换奇异性
通过链式变换与链式逆变换,可将链式系统的运动规划方法应用于非完整三关节机械手系统。然而,运动规划过程中我们发现,在某些边界条件约束下,虽然可以在链式空间内规划出各状态变量的运动轨迹,但这些轨迹从链式空间映射到关节空间中时,机械手某些关节的运动可能产生奇异现象。


图3 各关节角的运动轨迹Fig.3 The trajectory of each joint
此奇异现象是运动轨迹从链式空间映射到关节空间的过程中产生的,因此需先推导出链式逆变换表达式。链式变换表达式(4)表明关节角位移θ1、θ2与z2、z3变量之间的映射并不是单射,有多个关节向量θ对应同一个向量z,因此在求反余弦函数时应该先界定关节角θ1、θ2的运动范围。例如,关节角位移θ1、θ2的初始值与终止值均为正值时,可计算得链式逆变换表达式:
(6)
观察非完整机械手系统的链式逆变换表达式(式(6))发现其中存在反三角函数与二次开方运算,而这些运算对自变量有定义域的要求。如果状态变量的取值超出了一定范围,则会导致链式逆变换无实数解。如图4所示,在θ1产生奇异的时间段(3~10 s之间)状态变量z2的值大于零,这使得在链式逆变换时由开方计算得到的是复数解,从而导致了关节角θ1的链式逆变换奇异。这一实例表明,并不是链式空间中所有的点都可以通过链式逆变换映射到关节空间中。一旦在链式空间中规划出一条轨迹,其上的某一点或某些点链式逆变换无解,则关节角的运动就会产生奇异,我们将非完整机械手的这种性质称为链式逆变换奇异性。

图4 z的运动轨迹Fig.4 The trajectory of z parameter
这种由于链式逆变换而产生的奇异位形可以通过对状态变量附加不等式约束来规避,根据数学上对反三角函数及二次开方运算中自变量的定义域要求,可以确定z2、z3需满足的条件如下所示:
(7)
整理得
(8)
3 规避奇异位形的运动规划方法
对非完整三关节机械手的运动规划实际上是控制其三个关节角从给定的初始值运动到目标值,这是对机械手系统的边界条件约束。另一方面,为了规避机械手系统的链式逆变换奇异位形,还需要对状态变量的取值附加不等式约束条件,这一约束实际是限制了系统的空间位形,故称之为位形约束。在链式空间内规划的轨迹必须同时满足边界条件约束与位形约束,才能无奇异地映射成为关节空间内的可行轨迹。
3.1 边界条件约束
非完整三关节机械手的边界条件约束只限制θ1、θ2、θ3,称其为待控制状态变量,对φ2则没有边界条件约束,称其为自由状态变量。运动规划的目的是在有限的时间内求解有界控制输入u(t),使三个关节角分别从初始值出发,在终止时刻到达目标值。这样,就将非完整三关节机械手广义坐标向量中的自由变量分离出来,可将此自由变量的边界值作为待定系数通过运动规划求解。

(9)
其中,z2(T)、z3(T)、z4(T)表示控制输入为u(t)时各状态变量在终止时刻的值,是关于u(t)的函数。
3.2 位形约束
为了规避非完整三关节机械手的链式逆变换奇异位形,必须保证运动规划的轨迹能够完全地从链式空间映射到关节空间中,因此轨迹上的每一个点都应该是链式逆变换有解的。在之前的论述中已给出了链式空间中的一点向关节空间映射有实数解的条件(式(8)),该式中状态变量z2、z3相互耦合,且每增加一个不等式约束时算法的复杂度及计算时间也会大大增加。因此在实际的运动规划中可以根据具体情况选择其中的一个或几个不等式来作为非完整机械手系统的附加位形约束。
将系统链式空间中的一条轨迹L定义为:L={z(ti):ti∈[0,T],i=1,2,…,N},即将轨迹看作连续时间内一系列的点,并假设空间中可达的区域由不等式x(z)<0表示。为了处理这一不等式位形约束,定义如下函数:
(10)
其中,r>0,g(x)为一个连续光滑的函数。当x小于零时,函数g(x)为零,当x大于等于零时,g(x)随x单调递增,选取g(x)为
(11)
γ>0
即可将不等式约束方程x(z)<0转换为等式约束方程:
(12)
当轨迹上所有N个点均满足位形约束条件x(z)<0时,表明轨迹L在z变量的可达空间内,h的值为零,等式约束方程(式(12))不起作用;当存在某个或某些点不满足位形约束条件时,h的值为正数,约束方程(式(12))迫使轨迹L向可达空间内运动。
3.3 运动规划
在非完整三关节机械手系统所对应的链式空间内,将各状态变量的边界条件约束与为了规避链式逆变换奇异位形的附加约束结合起来,可以得到一个扩展的非线性方程组:
(13)
若将控制输入取为含有待定系数的多项式:
(14)
则边界条件及运动总时间已知时,f1、f2、f3、h均为关于待定系数的表达式,非完整三关节机械手的运动规划问题即可转化成为式(13)所示的非线性方程组的求解问题。
可以采用牛顿迭代法求解非线性方程组(式(13)),如下所示:
c(k+1)=c(k)-[G′(c(k))]+G(c(k))
(15)
其中,c为控制输入的待定系数,c=(c1,c2,c3,c4)T;G′(c)为G(c)的雅可比矩阵,G=(f1,f2,f3,h)T,[G′(c)]+为G′(c)的伪逆。
求解出链式空间中的控制输入表达式后,便可规划得链式空间中待控制状态变量的运动轨迹,再通过链式逆变换将轨迹映射到关节空间中,得到非完整机械手三个关节角的运动轨迹。在此过程中链式空间内对状态变量附加的位形约束能够保证规划的轨迹可完全映射至关节空间中,从而规避了机械手的链式逆变换奇异位形。
4 仿真与实验
增加位形约束后进行运动规划,得到链式空间中各状态变量的运动轨迹如图5所示,此时z2始终保持为负值,这说明链式空间中规划的轨迹可以完全地映射至关节空间中。通过链式逆变换求解出非完整机械手三个关节角的运动轨迹如图6所示。

图5 z的运动轨迹(加入位形约束后)Fig.5 The trajectory of z parameter (configuration constraint attached)

图6 各关节角的运动轨迹(加入位形约束后)Fig.6 The trajectory of each joint (configuration constraint attached)
在非完整三关节机械手运动控制实验平台(图7)开展实验研究,利用两个伺服电机作为非完整机械手的控制输入,并通过UMAC控制器控制伺服电机的运动,通过角位移传感器测量各关节角实际运动的角位移。非完整三关节机械手三个关节角的实际运动轨迹如图8所示。

图7 运动控制实验平台Fig.7 Motion control experimental platform
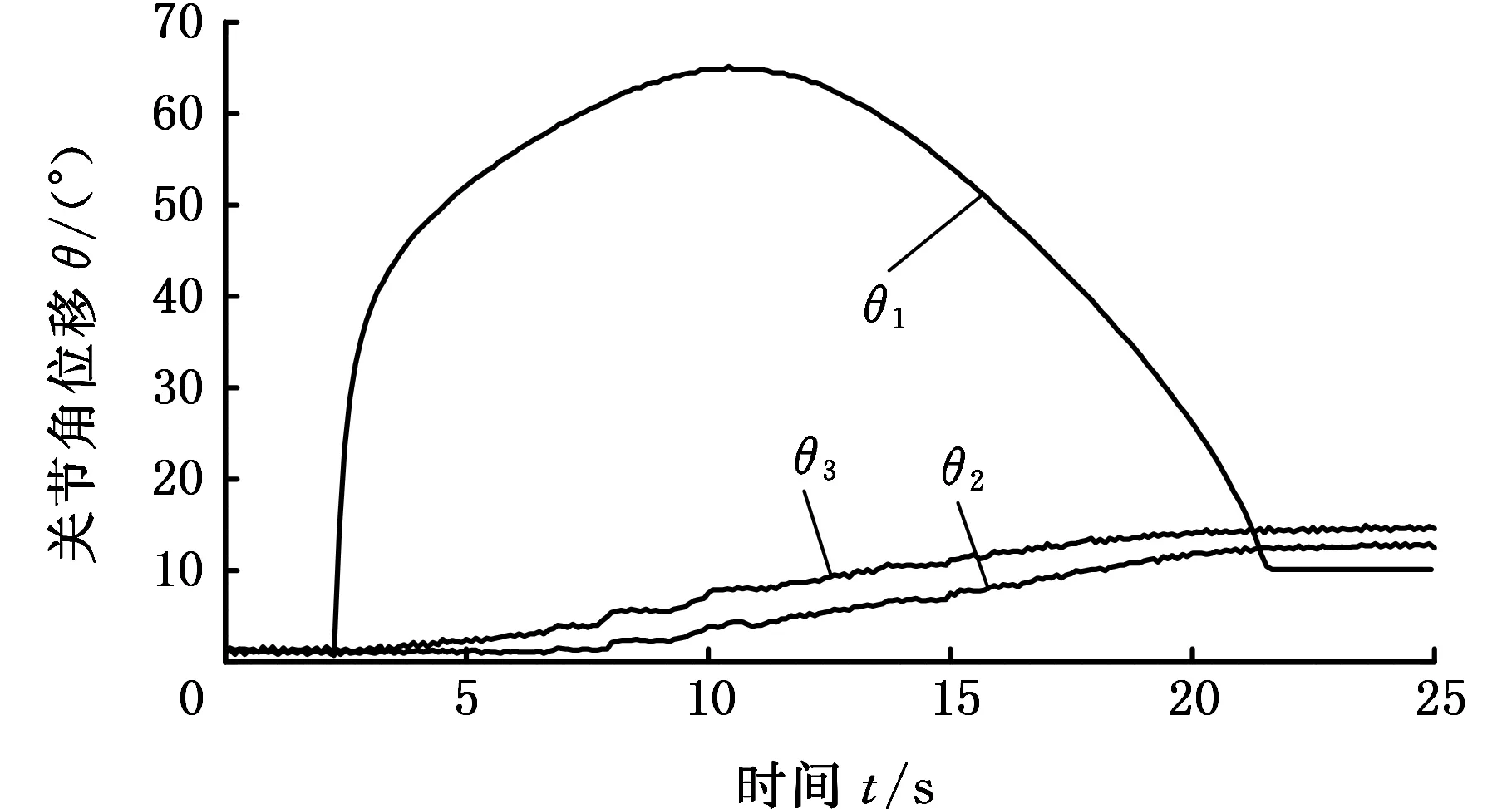
图8 各关节角的实际运动轨迹Fig.8 The experimental trajectory of each joint
对比仿真与实验结果,机械手三个关节角位移的运动趋势基本相同,这表明本文提出的运动规划方法可以实现对非完整三关节机械手的有效控制。
5 结论
(1)依据非完整机械手的结构特征,将广义坐标向量中的自由状态变量分离出来,并利用边界值作为待定系数进行求解,明确了一类可链式化机械手路径规划的基本方法。
(2)从非完整机械手的运动学模型及其变换特点出发,探讨了运动规划的方法以及存在奇异位形的原因——链式逆变换解的奇异性,并提出了保证链式逆变换可行的不等式约束条件。
(3)建立了一种可规避奇异位形的运动规划方法,即利用罚函数将不等式约束转化为等式约束后,将其与边界条件约束结合起来形成一个非线性方程组,通过牛顿迭代法求解链式系统的控制输入,规划出一条从链式空间无奇异地映射到关节空间中的路径。计算仿真和实验表明所提出的运动规划方法是有效的。
[1] DULEBA I, KHEFIFI W, KARCZ-DULEBA I. Layer, Lie Algebraic Method of Motion Planning for Nonholonomic Systems[J]. Journal of the Franklin Institute, 2012, 349(1):201-215.
[2] MURRAY R M, SASTRY S S. Steering Nonholonomic Systems in Chained Form[C]//IEEE Conference on Decision & Control. Brighton, 1991:1121-1126.
[3] TILBURY D, MURRAY R M, SASTRY S S.Trajectory Generation for the N-trailer Problem Using Goursat Normal Form[J]. IEEE Transactions on Automatic Control, 1995, 40(5):802-819.
[4] LOOCK W V, PIPELEERS G, DIEHL M, et al. Optimal Path Following for Differentially Flat Robotic Systems through a Geometric Problem Formulation[J]. IEEE Transactions on Robotics, 2014, 30(4): 980-985.
[5] JANIAK M, TCHONA K. Towards Constrained Motion Planning of Mobile Manipulators[C]//IEEE International Conference on Robotics and Automation. Anchorage, 2010:4990-4995.
[6] TAN T G, LI L, LIU M Y, et al. Design and Path Planning for Controllable Underactuated Manipulator[J]. International Journal of Advancements in Computing Technology, 2012, 4(2): 212-221.
[7] NAKAMURA Y, CHUNG W, SORDALEN O J. Design and Control of the Nonholonomic Manipulator[J]. IEEE Transactions on Robotics & Automation, 2001, 17(1):48-59.
[8] SORDALEN O J. Conversion of the Kinematics of a Car with N Trailers into a Chained Form[C]//IEEE International Conference on Robotics and Automation. Atlanta, 1993: 382-387.
[9] KORAYEM M H, NAZEMIZADEH M, RAHIMI H N. Trajectory Optimization of Nonholonomic Mobile Manipulators Departing to a Moving Target Amidst Moving Obstacles[J]. Acta Mechanica, 2013, 224(5):995-1008.
[10] TAN Y G, JIANG A Q, ZHOU Z D. A Nonholonomic Motion Planning and Control Based on Chained Form Transformation[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Beijing, 2006: 3149-3153.
[11] 谭跃刚. 非完整机器人的原理与控制[M].北京:科学出版社,2011:76-82. TAN Yuegang. Principle and Control of Nonholonomic Robots[M]. Beijing: Science Press, 2011:76-82.
(编辑 王旻玥)
Chained Form Conversion and Motion Planning Method for a Nonholonomic Manipulator
LI Liang1LIU Yifang2TAN Yuegang3
1.School of Mechatronic Engineering,Baoji University of Arts and Sciences,Baoji ,Shaanxi,7210072.China Chang Jiang Energy Corp.(Group),Wuhan,4300703.School of Mechanical and Electronic Engineering,Wuhan University of Technology,Wuhan,430070
A motion planning algorithm was proposed to avoid the inverse chained form conversion singularity of nonholonomic three-joint manipulators. Free variables of generalized coordinates were separated according to the structural features of nonholonomic manipulators. Then the boundary values of variables acted as undetermined coefficients of control inputs. Inequality constraints were proposed to make sure that a trajectory in chained form spaces might be mapped into joint spaces for singularity of inverse chained form conversion. Additional constraints were used to avoid singular configuration of the inverse chained form conversion. Results of simulations and experiments prove the feasibility and effectiveness of this motion planning algorithm.
nonholonomic manipulator; chained form conversion; singular configuration; motion planning
2016-09-18
陕西省自然科学基础研究计划资助项目(2016JM5019);陕西省教育科学“十三五”规划资助项目(SGH16H161);宝鸡科技计划资助项目(16RKX1-30)
TP24
10.3969/j.issn.1004-132X.2017.16.010
李 亮,男,1979年生。宝鸡文理学院机械工程学院讲师、博士。主要研究方向为机器人技术与控制。发表文章10余篇。E-mail:leeliang@126.com。刘一方,女,1990年生。中国长江动力集团有限公司汽轮机研究所工程师。谭跃刚,男,1959年生。武汉理工大学机电工程学院教授、博士研究生导师。

