基于拓扑优化方法的大型液压挖掘机斗杆新型结构

宁晓斌 刘亚冉 李 颉 李 光 李佳林

1.浙江工业大学机械工程学院，杭州,3100142.英国帝国理工学院航空系，伦敦，SW72AZ 3.太原重工股份有限公司,太原,030024

基于拓扑优化方法的大型液压挖掘机斗杆新型结构

宁晓斌1刘亚冉1李 颉2李 光3李佳林3

1.浙江工业大学机械工程学院，杭州,3100142.英国帝国理工学院航空系，伦敦，SW72AZ 3.太原重工股份有限公司,太原,030024

以斗杆结构强度为基准，采用结构优化的方法，设计了大型液压挖掘机正铲工作装置斗杆新结构。采用离散元方法，构建矿山岩石模型，获得铲斗挖掘阻力；采用多体动力学方法，搭建大型液压挖掘机正铲工作装置刚柔耦合动力学模型，获得挖掘机斗杆挖掘工况斗杆动态载荷，并对斗杆进行动态结构强度分析；采用SIMP插值函数的变密度拓扑优化方法，在有限元中对斗杆结构进行拓扑优化设计，获得大型液压挖掘机正铲工作装置新型斗杆结构；对新型斗杆结构进行动态结构强度分析，斗杆结构强度保持原有水平。研究结果表明，通过拓扑优化后得到的新型斗杆，结构强度与类比设计一致，但质量减小。

有限元；拓扑优化；变密度法；挖掘机

0 引言

随着矿山设备高效、低排放需求，采掘设备向大型化发展，国内超过200 t大型液压挖掘机保有量持续增加，但国产仅有WYD260大型液压挖掘机进行矿山作业。该挖掘机整机质量260 t，铲斗容量15 m3，其驱动电机功率为1000 kW；而进口铲斗容量15 m3的液压挖掘机，其驱动电机功率仅为700～750 kW，由此可知，我国大型液压挖掘机设计仍然与国外存在差距。

由于大型液压挖掘机被卡特彼勒、小松、利勃海尔和日立四大工程机械公司垄断，大型液压挖掘机设计方法从未公开，国内大型液压挖掘机核心技术掌握不够。与大型液压挖掘机不同,小型挖掘机作业对象主要是沙土。以小型反铲液压挖掘机工作装置质量和耐久性为目标，KIM[1]开发了优化设计方法及程序，能够在相对较短的时间内实现工作装置的自动设计，包括有限元自动建模、应力分析，疲劳寿命计算，形状和厚度的优化；PARK[2]以可靠的动臂疲劳强度和较低的生产成本为优化目标，基于应力分析获得应力分布，重新配置动臂结构，得到一个较为合理的动臂结构；ÖZGEN[3]运用一种柔性优化设计软件，结合遗传算法对小型液压挖掘机的动臂进行形貌优化研究，优化后的动臂在满足强度与可靠性的条件下，减轻了质量；WU等[4]运用拓扑优化的方法，对小型挖掘机动臂内部加强筋重新布置，减轻了动臂应力集中问题；邓志勇等[5]以小型反铲挖掘机动臂质量最小化为目标函数，以动臂各单元的相对密度为设计变量，强度和刚度为约束条件，采用变密度法，对动臂进行了轻量化设计。周全[6]利用有限元优化方法对WYD260挖掘机的斗杆进行了拓扑优化，但未提出完善的斗杆结构。针对小型液压挖掘机工作装置的研究主要集中在静态结构分析，而大型液压挖掘机在矿山的作业对象主要是松散岩石，工作装置冲击载荷大，为研发具有自主知识产权的大型液压挖掘机，本文探索了大型液压挖掘机工作装置结构优化设计方法。太原重工股份有限公司研制的国产首台大型液压挖掘机WYD260在准格尔某矿山投产，整机性能稳定，铲装岩石满斗率90%以上[7-8]。该公司以WYD260为基础，研制了WYD390型(整机质量390 t，铲斗容量22 m3)挖掘机[9-10]，并正在研发WYD600型(整机质量600 t，铲斗容量32 m3)大型液压挖掘机。

本文针对WYD600型正铲液压挖掘机的研发，建立工作装置刚柔耦合模型，依据铲斗挖掘阻力，对挖掘机工作装置进行动态结构强度分析；基于有限元软件拓扑优化方法[11]，利用变密度法[12]，对挖掘机斗杆的结构拓扑优化和优化后的结构强度进行分析。

1 大型正铲液压挖掘机作业载荷分析

离散元方法在研究松散岩石颗粒动力学特性中得到应用[13-14]。采用离散元方法，基于岩石材料特性、岩石块度分布和分形分布，建立准格尔某矿山松散岩石矿堆模型，按照WYD260挖掘机斗杆挖掘工况，分析得出松散岩石对铲斗的挖掘阻力，将挖掘阻力施加在工作装置多体动力学刚体模型上，测量得出斗杆挖掘工况斗杆油缸、动臂油缸的压力，对比WYD260挖掘机在矿山斗杆挖掘工况动臂油缸、斗杆油缸压力实测值，二者基本吻合，建立的离散元岩石模型比较准确地模拟了大型挖掘机铲斗的挖掘阻力[15]。

WYD600挖掘机与WYD260挖掘机同样采用正铲工作装置。在所建立的松散岩石模型上，进行WYD600挖掘机斗杆挖掘工况下铲斗挖掘阻力分析，得到铲斗挖掘阻力，如图1所示，图中曲线分别表示铲斗挖掘阻力，挖掘阻力在X、Y、Z方向的分力(铲斗在XZ平面运动)。

图1 挖掘阻力Fig.1 Digging resistance

2 挖掘机正铲工作装置动态结构强度分析

大型液压挖掘机正铲工作装置由动臂、斗杆、铲斗和油缸组成，首先在多体动力学软件MSC.ADAMS中建立工作装置的刚体模型，然后采用HyperMesh对动臂、斗杆划分网格并导入多体动力学软件，将动臂、斗杆替代为柔性体部件，铲斗、油缸仍然为刚性部件，通过约束连接各零部件，建立工作装置刚柔耦合模型。

动态结构强度分析在工作装置刚柔耦合模型中进行。在MSC.ADAMS中，将图1所示的挖掘阻力加载到工作装置刚柔耦合模型的铲斗上，通过驱动函数控制铲斗挖掘轨迹与离散元铲斗挖掘轨迹基本一致，模拟挖掘机斗杆挖掘。斗杆挖掘工况工作装置某时刻结构应力云图见图2，该时刻斗杆应力达到峰值，最大应力为108.99 MPa。

图2 工作装置von Mises应力云图Fig.2 Von Mises stress contour of the working device

斗杆应力达到峰值时刻，斗杆各铰接点三个方向上的受力如表1所示。

表1 斗杆应力峰值时铰接点的受力情况Tab.1 Hinge force with maximum stress N

3 斗杆拓扑优化

3.1 拓扑优化模型的建立

挖掘机工作装置的性能基本决定着挖掘机的作业效率与能耗。工作装置要求质量轻、强度高、耐久性强。挖掘机最常见的作业方式是斗杆挖掘，斗杆在斗杆挖掘工况受到的载荷与冲击较大，如果斗杆质量过大，会降低挖掘效率，因此斗杆结构优化目标是在保证强度和稳定性的前提下减轻质量。

拓扑优化设计是用来在给定的设计空间内确定结构的形状、材料分布或传力途径的一种优化方法。连续体拓扑优化方法主要有均匀化方法[16-17]、变密度法以及渐进结构优化法[18]。变密度法计算效率高，应用广泛，本文采用变密度法，应用有限元软件对斗杆进行拓扑优化。对斗杆结构而言，各个铰接孔的位置及尺寸是在工作装置整体结构设计阶段决定的，故在优化设计过程中必须作为非设计区域加以保留(图3深色区域)。剩下的结构作为设计区域(图3浅色区域)，拓扑计算只改变该区域的单元密度值。在斗杆各个铰接处创建刚性连接，用于对斗杆施加约束和载荷。与铲斗铰接处(图3的A铰接处)为全约束；与动臂铰接处(图3的B铰接处)仅不约束绕Y轴的转动；与油缸铰接处(图3的C铰接处)约束Y轴方向的移动和绕X、Y轴的转动，在沿X轴与Z轴方向施加载荷。把斗杆挖掘过程中，斗杆结构最大应力时刻斗杆油缸对斗杆的作用力加载到斗杆油缸铰接点。

图3 斗杆有限元网格模型Fig.3 The finite elements model of stick

拓扑优化目标为体积分数最小。优化目标是使用材料最少，使斗杆结构质量减轻，实现斗杆结构轻量化设计。

拓扑优化的设计变量为设计区域里每个单元的密度。拓扑结构单元密度在0～1.0之间，通过改变单元密度，得到不同的拓扑结构密度云图。

针对斗杆设计变量，定义了五种设计约束，分别为最小成员尺寸控制约束、对设计区域进行对称约束的制造工艺约束、对设计区域的应力水平约束、体积比约束以及位移约束。具体设定如下：

(1)添加对最小成员尺寸控制约束可以保证拓扑结构中单元密度是1的位置处，结构的最小尺寸大于设定值。最小成员尺寸约束可以避免细小传力结构的产生，使材料的拓扑更加均匀化。一般最小成员尺寸为网格的3倍左右，故最小成员尺寸设定值为120 mm。

(2)由于斗杆关于纵向平面(XZ平面)左右对称，故需对设计区域进行模式组制造工艺约束。无论有限元模型的网格、载荷和边界约束是否对称，模式组对称约束均可以保证结构拓扑密度分布关于纵向平面对称，在没有承受对称力的情况下得到对称结构，便于加工制造。

(3)斗杆采用某合金材料，最大许用应力为680 MPa，考虑到设计的安全系数，将设计区域结构受到的最大应力控制在350 MPa，将其设置为设计区域的应力水平约束。

(4)设置不同的体积比约束，得到不同的拓扑结果，体积约束过大会造成大量的材料堆积，体积约束过小会造成结构应力分布集中。把体积比约束设置在0.1～0.3之间，选择满足要求的、结构特点分明的一组作为最终的拓扑结果。

(5)拓扑优化的目标是减少材料使用，但是，减少材料后可能导致模型刚度的降低以及变形的加剧，因此，在优化过程中需要确定位移约束，这样可以保证在使用的材料和模型的总体刚度上达到一定的平衡。将载荷作用点的合成位移的上限设为1.0 mm。

创建应变能响应函数，将寻求设计区域应变能的最小值定义为目标函数，结构材料的体积和位移作为限制，即拓扑优化的目标是，在满足以上所有约束条件的前提下，寻求刚度最大和变形最小的新斗杆结构。

优化求解计算前，将最大优化设计迭代系数(DESMAX)设为80，为了获得比较清晰的拓扑结构，离散参数(DISCRETE)取2.0。

3.2 拓扑优化结果及分析

(a)体积比约束0.1

(b)体积比约束 0.15

(c)体积比约束0.2

(d)体积比约束0.25图4 拓扑结构单元密度云图Fig.4 Elements density contour of the topological strcture

(a)体积比约束0.1

(b)体积比约束 0.15

(c)体积比约束0.2

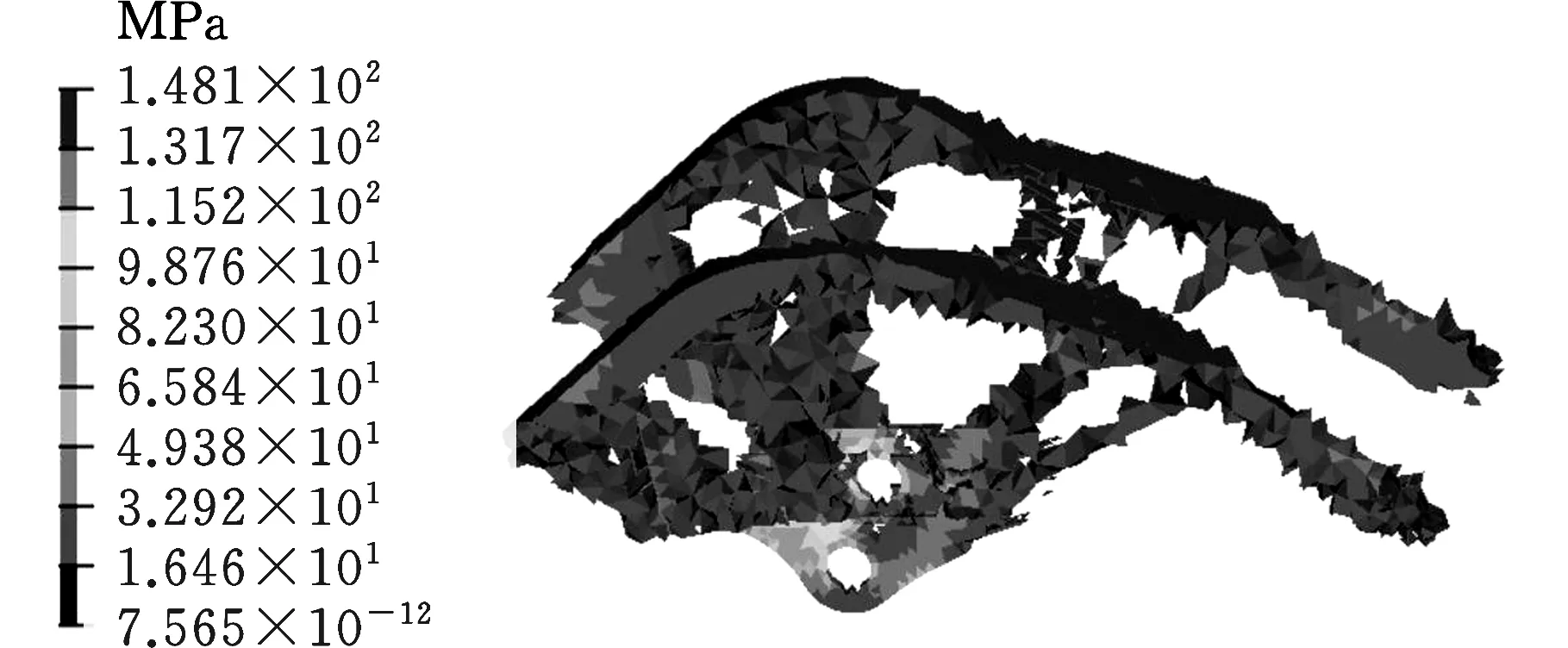
(d)体积比约束0.25图5 拓扑结构应力云图Fig.5 Stress contour of the topological structure

优化求解计算完成后，查看单元密度云图，设置单元密度云图显示密度值超过0.3的部分。分别对体积比约束(最多保留体积)为0.1、0.15、0.2、0.25的拓扑结构进行对比分析，如图4所示。查看对应的拓扑结构应力云图，如图5所示。图4对单元密度值小于0.3区域的材料做了去除处理，图中显示的深色区域的单元密度为1，表示该区域的材料很重要，需要保留；浅色区域密度值小，表明该处材料保留少，结构可以做适当的改变。图5中，四种结构应力均小于许用应力，最大应力位置位于斗杆油缸铰接处附近。综合分析拓扑结构单元密度云图和应力云图,体积比约束为0.1的拓扑优化单元密度云图材料分布清晰，无过多的材料堆积，且应力主要集中在载荷施加位置附近，其他位置应力较小，符合拓扑优化设计要求。故选择体积比约束为0.1的拓扑结构为拓扑优化结果。

导出斗杆拓扑优化CAE网格模型，如图6所示。

图6 拓扑后的CAE模型Fig.6 CAE model after topology

4 斗杆拓扑结构优化设计

4.1 斗杆拓扑结构静力学分析

拓扑优化结构为概念设计结构，拓扑优化模型存在结构不连续、形状不规则等缺陷，不符合实际制造要求。在拓扑模型基础上，对斗杆结构进行重新设计。斗杆结构仍然选择钢板焊接而成，用平整的钢板替代不规则的面板，将细小的部位连成一个整体。对整理过的斗杆拓扑结构重新进行网格划分，并在各铰接点施加约束和载荷，在有限元软件中进行静力学分析，得到图7所示的应力云图，最大应力为189.2 MPa。

图7 拓扑结构静力学分析von Mises应力云图Fig.7 Von Mises stress contour of static analysis

4.2 斗杆拓扑结构动态强度分析及优化

将拓扑斗杆结构网格导入多体动力学软件，替代原斗杆柔性体，同样地，进行斗杆挖掘工况动态仿真分析。斗杆最大应力时刻的应力云图见图8，最大应力653.7 MPa，由于斗杆应力过大，需对斗杆结构进一步优化设计。

图8 拓扑结构动力学分析von Mises应力云图Fig.8 Von Mises stress contour of topological structure in dynamical analysis

去除圆形柱体，用箱形梁代替，利于加工制造；高应力区域为拉应力，可以在斗杆底部加两个箱型梁，缓解顶部的应力集中。对应力大的板适当增大板厚，应力小的板适当减小板厚。再次优化设计的斗杆结构网格模型如图9a所示，导入多体动力学软件中，进行斗杆挖掘工况结构分析，斗杆结构强度应力云图见图9b，斗杆最大应力为129.58 MPa。斗杆较图8结构应力有很大的减小，但结构局部应力集中明显，底部下梁与中间四根支撑梁交叉在一起，不利于制造。

(a)优化后斗杆CAE模型

(b)新斗杆动力学分析von Mises应力云图图9 优化后斗杆结构Fig.9 The strcture of stick after opimization

将中间四根支撑梁移动到上下两跟箱型梁之间，可以改善结构的稳定性，利于斗杆的加工制造，但同时会使得斗杆底板受到较大的剪切力，大大增大了底板的应力。提出两种方案对底板应力大的问题进行优化，方案一是保持斗杆油缸铰接位置不变，通过改变底板结构来缓解底板应力过大的问题；方案二是增大两个斗杆油缸间的距离，使底板受到的剪切力减小。

(a)优化后斗杆CAE模型

(b)优化后斗杆动力学分析von Mises应力云图图10 优化后斗杆结构一Fig.10 The first strcture of stick after opimization

(a)优化后斗杆CAE模型

方案一：在底板上方再创建一块板，可以减小底板的受力，两板之间通过建立加强板使斗杆底部构成一箱体，提高结构的稳定性，改善该区域的应力。斗杆油缸铰接位置增加两块耳板，缓解下梁和铰接耳板应力过大的问题。四根支撑梁板厚也可以适当减小，减小斗杆质量。斗杆上部增加一根横梁可以保证斗杆结构的稳定性，也可以有效缓解横梁的受力，同时可以减小底部箱体的受力。修改后的斗杆网格模型如图10a所示，斗杆钢板厚度为45 mm、35 mm、20 mm三种；同理，在多体动力学软件中进行挖掘机工作装置斗杆挖掘工况分析，修改后的新斗杆动力学分析应力云图见图10b，最大应力为106.93 MPa，质量为15.6 t。

(b)优化后斗杆动力学分析von Mises应力云图图11 优化后斗杆结构二Fig.11 The second strcture of stick after opimization

方案二：将两个斗杆油缸沿Y轴方向适当外移，增大油缸铰接点之间的距离，使斗杆受力点靠近两根下梁，并保证油缸之间的安装距离。按照方案一的做法，用箱体代替底板，增加一根横梁，增大结构的稳定性。钢板的厚度减小为40 mm、30 mm、20 mm。新斗杆CAE模型如图11a所示，动力学分析应力云图见图11b。最大应力为57.08 MPa，质量为13.6 t。

对比优化前斗杆结构与优化后斗杆结构在同一挖掘工况下的应力、斗杆质量、板厚，如表2所示。

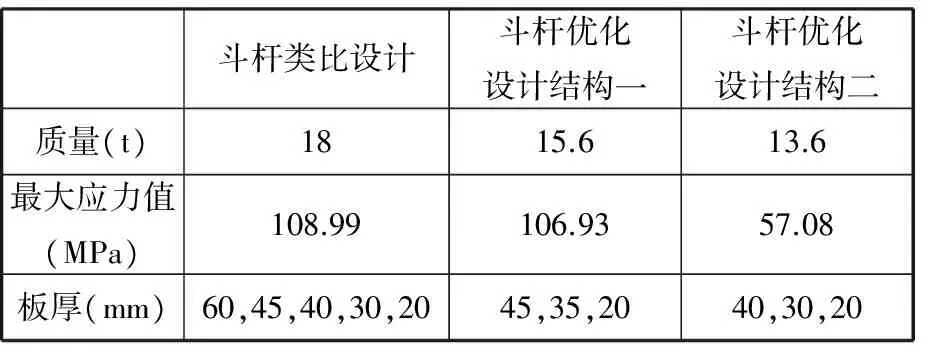
表2 优化前斗杆与优化后斗杆结果对比Tab.2 Comparison between the former and the later stick

比较优化后设计的斗杆新结构与原设计的斗杆结构，在不降低结构强度的前提下降低了质量，相关设计方法与结构已申请专利。大型液压挖掘机正铲工作装置关键结构件设计方法是挖掘机研发的核心技术之一，本文的设计方法在大型液压挖掘机工作装置设计上具有较高的参考价值。

5 结论

(1)采用离散元方法建立矿山松散岩石模型，分析计算了大型挖掘机铲斗挖掘阻力。

(2)在多体动力学软件中建立大型液压挖掘机正铲工作装置刚柔耦合模型，全面分析挖掘机工作装置动态结构强度，并对类比设计、重新设计的斗杆结构进行了动态结构强度分析，确保了斗杆优化设计后结构的可靠性。

(3)基于变密度法的拓扑优化技术，运用有限元软件对挖掘机斗杆进行了拓扑优化。考虑斗杆拓扑结构的可制造性等因素，对结构进行了优化设计。优化后的新型斗杆结构强度与原结构保持不变，但质量减轻。挖掘机作业循环过程中，斗杆重心始终与挖掘机整机重心保持较大的距离，减轻斗杆质量，不仅增加了挖掘机作业效率，而且增加了挖掘机作业的稳定性。

[1] KIM S Y. A Development of the Virtual Design System for the Attachments of a Hydraulic Excavator[J]. SAE International Journal of Commercial Vehicles, 2012, 5(1):327-332.

[2] PARK S C. Design of Excavator Boom Structure Based on Fatigue Strength of Weldment(II)[J]. Journal of the Korea Society for Power System Engineering, 2011, 29(4)：61-66.

[3] ÖZGEN C. Shape Optimization of an Excavator Boom by Using Genetic Algorithm[D]. Ankara:Middle East Technical University，2008.

[4] WU S B， LIU X B. Layout Topology Optimization for Inner Stiffeners of Excavator’s Boom[J]. Advanced Materials Research，2014(915/916)：240-243.

[5] 邓志勇，熊昌炯，洪昊，等. 变密度法在挖掘机动臂轻量化设计中的分析与应用[J]. 三明学院学报，2016，33 (2)：66-73. DENG Zhiyong，XIONG Changjiong, HONG Hao，et al. Analysis and Application on Variable Density Method in the Process of the Excavator Boom Lightweight Design[J]. Journal of Sanming University，2016，33 (2)：66-73.

[6] 周全. 正铲液压挖掘机工作装置动态强度分析与结构优化[D]. 杭州：浙江工业大学，2015. ZHOU Quan. Research on Dynamic Strength and Structure Optimization of Face-shovel Hydraulic Excavator Attachment[D]. Hangzhou：Zhejiang University of Technology，2015.

[7] 朱小晶，权龙，王新中，等. 大型液压挖掘机工作特性联合仿真研究[J]. 农业机械学报，2011，42(4)：27-32. ZHU Xiaojing，QUAN Long，WANG Xinzhong，et al. Co-simulation Analysis of Working Characteristic for Large Hydraulic Excavator[J]. Transactions of the Chinese Society for Agricultural Machinery，2011，42(4)：27-32.

[8] 朱小晶，权龙，王新中，等. 大型矿用正铲液压挖掘机水平推压特性联合仿真[J]. 农业机械学报，2011，42(5)：30-34. ZHU Xiaojing，QUAN Long，WANG Xinzhong，et al. Co-simulation of Flat-pushing Characteristics of Large Mining Face-shovel Hydraulic Excavator[J]. Transactions of the Chinese Society for Agricultural Machinery，2011，42(5)：30-34.

[9] 张羽林，宁晓斌，王秋成. 大型正铲液压挖掘机工作装置性能的优化仿真[J]. 机电工程，2013，30(3)：329-332. ZHANG Yulin，NING Xiaobin，WANG Qiucheng. Optimization Simulation for Performance of Working Device of Large Face-shovel Hydraulic Excavator[J]. Journal of Mechanical & Electrical Engineering，2013，30(3)：329-332.

[10] 陈露丰, 宁晓斌. 液压挖掘机工作装置的动态强度仿真分析[J]. 机电工程，2013，30(8)：924-928. CHEN Lufeng，NING Xiaobin. Simulation and Analysis of Dynamic Strength of Working Mechanism of Hydraulic Excavator[J]. Journal of Mechanical & Electrical Engineering，2013，30(8)：924-928.

[11] THOMAS H，SCLLRAMM U. Issues of Commercial Optimization Software Development[J]. Structural and Multidisciplinary Optimization，2002，23(2)：97-110.

[12] BENDSØE M P. Optimal Shape Design as a Material Distribution Problem[J]. Structural and Multidisciplinary Optimization，1989，1(4)：193-202.

[13] THORNTON C，CUMMINS S J，CLEARY P W. An Investigation of the Comparative Behaviour of Alternative Contact Force Models during Inelastic Collisions[J]. Powder Technology，2013，233：30-46.

[14] HÖHNER D，WIRTZ S，KRUGGEL-EMDEN H，et al. Comparison of the Multi-sphere and Polyhedral Approach to Simulate Non-spherical Particles within the Discrete Element Method：Influence on Temporal Force Evolution for Multiple Contacts[J]. Powder Technology，2011，208:643-656.

[15] 陈烨，李爱峰，李光，等. 大型液压挖掘机斗杆挖掘阻力的离散元方法研究[J]. 机电工程，2015，32(6)：798-802. CHEN Ye，LI Aifeng，LI Guang，et al. DEM Research for Crowd Force of Large Hydraulic Excavator[J]. Journal of Mechanical & Electrical Engineering，2015，32(6)： 798-802.

[16] BENDSØE M P，KIKUCHI N. Generating Optimal Topologies in Structural Design Using a Homogenization Method[J]. Computer Methods in Applied Mechanics and Engineering，1988，71：197-224.

[17] SUZHKI K，KIKUCHI N. A Homogenization Method for Shape and Topology Optimization[J]. Computer Methods in Applied Mechanics and Engineering，1991，4：17-22.

[18] XIE Y M，STEVEN G P. A Simple Evolutionary Procedure for Structural Optimization[J]. Computer&Structures，1993，49(5)：885-896.

(编辑 王旻玥)

New Stick Structures of Large Hydraulic Excavators Using Topology Optimization Method

NING Xiaobin1LIU Yaran1LI Jie2LI Guang3LI Jialin3

1.College of Mechanical Engineering,Zhejiang University of Technology,Hangzhou,3100142.Department of Aeronautics,Imperial College London，London,SW72AZ3.Taiyuan Heavy Industry Co.,Ltd.,Taiyuan,030024

Based on the structural strengths of the sticks, a new stick structure of the working devices of large shovel hydraulic excavators was designed by the method of structure optimization. Mine rock model was build by using the discrete element method, and the digging resistances of the bucket were obtained. The rigid-flexible coupling model of the working devices of the large shovel hydraulic excavators was established by using the multi-body dynamics method, the dynamic loads of the sticks during the stick digging were obtained, and the dynamic structural strengths of the sticks were analyzed. The topology optimization design of the stick structures in finite element was carried out by using the variable density topology optimization method of SIMP interpolating function, and the new stick structures of the working devices of large shovel hydraulic excavators were obtained. The dynamic structure strengths of the new stick structures were analyzed, the strengths of the new stick structures maintained the original level. The results indicate that the new stick structure has the same strength as the analogy designed, while the weights of the sticks are reduced.

finite element; topology optimization; variable density method; excavator

2016-10-26

国家自然科学基金资助项目(51375452);山西省煤基重点科技攻关项目(MJ2014-01)

TH122

10.3969/j.issn.1004-132X.2017.16.007

宁晓斌，男，1965年生。浙江工业大学机械工程学院副教授。主要研究方向为机械优化设计、工程车辆能量回收方法。发表论文20余篇。刘亚冉，男，1990年生。浙江工业大学机械工程学院硕士研究生。李 颉，男，1991年生。英国帝国理工学院航空系硕士研究生。李 光，男，1982年生。太原重工股份有限公司技术中心工程师。李佳林，男，1983年生。太原重工股份有限公司技术中心工程师。