TTI各向异性逆时偏移技术及应用
王咸彬
(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)
TTI各向异性逆时偏移技术及应用
王咸彬
(中国石油化工股份有限公司石油物探技术研究院,江苏南京211103)
地下介质广泛存在各向异性,传统各向同性地震偏移成像技术往往会导致成像精度不高甚至深度偏差问题,宽方位采集技术和高精度逆时偏移(RTM)成像技术的应用更是突显了各向异性的影响。从弱各向异性弹性波波动方程出发,首先采用拟声波近似得到VTI各向异性伪声波控制方程,然后引入交叉导数项进行坐标旋转得到TTI各向异性伪声波控制方程,再由高阶有限差分方法得到TTI-RTM偏移算子,最后采用波场校正消除横波分量影响,提高各向异性偏移算子的精度。模型试算和实际资料处理结果表明,该技术在处理各向异性介质地震资料时具有更高的精度,是高精度地震成像理想的技术手段。
各向异性;拟声波近似;控制方程;TTI逆时偏移
地下介质具有广泛的各向异性特性,如我国东部陆相砂泥岩薄互层具有长波长各向异性特征,西部海相岩溶—裂缝型碳酸盐岩储层具有裂隙诱导各向异性特征。随着宽方位地震数据采集技术的推广应用,各向异性对地震成像效果的影响更加突出。逆时偏移(RTM)等地震成像技术因其在克服偏移孔径和偏移倾角限制方面的理论优势越来越得到工业界的认可,但大偏移孔径和大偏移倾角容易引入TTI各向异性的影响,传统的以各向同性介质为物理假设的RTM技术往往存在成像精度不高、地震分辨率降低、甚至成像深度与实际位置存在偏差等问题[1-6]。因此,需要发展TTI各向异性RTM技术以提高成像精度和地震分辨率、恢复真实的成像深度、消除井震误差,提高钻井成功率。
波兰科学家RUDZKI[7]于19世纪末20世纪初首次提出地下介质存在各向异性效应;GASSMANN[8]于20世纪50年代开展了各向异性对地震波传播影响方面的研究;20世纪70年代,LEVIN[9]描述了椭圆各向异性介质中反射波、折射波和多次波的特性,从而为各向异性介质地震处理方法研究奠定了理论基础;20世纪90年代,TSVANKIN等[10]推导了各向异性介质反射波时距曲线方程,在各向异性介质地震资料处理及成像技术的发展历程中起到了里程碑的作用。21世纪初,各向异性介质地震成像方法得到飞速发展,SUN等[11]在PS波Kirchhoff叠前时间偏移方法中,除了考虑介质的各向异性,同时还引入了变速介质走时计算公式;周巍等[12]研究了各向异性Kirchhoff叠前深度偏移算法和各向异性介质参数提取方法;GUO等[13]、刘礼农等[14]、吴国忱等[15]、梁锴等[16]研究了三维各向异性介质中的波动方程叠前深度偏移方法;ZHU等[17]通过修改运动学和动力学射线追踪方程组将高斯束偏移方法发展到各向异性介质,分别实现了叠后和叠前各向异性高斯束偏移;张凯等[18]将各向异性高斯束偏移拓展到角度域;王伟国等[19]提出了伪谱法逆时偏移技术,能够很好地近似Thomsen精确方程,但是精度偏低;王娟等[20]提出不完全的声波近似波场模拟方法,与弹性波模拟方法相比,明显提高了逆时偏移的计算效率,保证了长时间的稳定模拟,但是模拟中依然存在横波干扰;FLETCHER等[21]、DU等[22-23]提出了精确的弹性波逆时偏移方法,但无法实现纯纵波逆时偏移。
本文在前人研究的基础上,基于Thomsen参数推导了VTI各向异性伪声波控制方程,描述了VTI介质地震波传播规律,根据TTI介质和VTI介质的不同,引入交叉导数项通过坐标旋转得到了对称轴倾斜的TTI各向异性伪声波控制方程,进一步采用声波近似下的波场校正消除横波分量,得到TTI各向异性RTM偏移算子,最后通过三维盐丘模型试算和工区实际资料处理验证了TTI逆时偏移方法的有效性与实用性。
1 方法原理
1.1 弱各向异性介质中的波动方程
EULER根据位移、形变、应变与应力的关系,利用广义Hooker定律和牛顿第二定律建立了线性弹性动力学运动方程的一般表达式:
(1)
式中:ρ表示介质的密度;u表示质点的位移场;下标i,j,k,l表示笛卡尔坐标系中的任意一个维度;cijkl表示四阶刚度张量,即Hooker定律中应力与应变的关系张量;f表示单位质量、单位体积介质所受的外力。
由于利用弹性系数刚度矩阵不能直观地表示各向异性的强度,为此,THOMSEN[24]引入5个各向异性参数来描述弹性介质中的弱各向异性特性,每个参数都是弹性参数的函数,并且有明确的物理意义。
(2)
式中:vP0和vS0分别为P波和S波垂直TI介质各向同性地层的相速度;ε是P波各向异性强度的度量,ε=0意味着纵波无各向异性,ε越大,介质的纵波各向异性越强;δ是纵横波速度比的相关参数;γ是度量横波各向异性和横波分裂强度的参数,γ=0时横波无各向异性,γ越大介质的横波各向异性强度越大。利用ε,γ和δ可以表征弱VTI介质中弹性矩阵元素:
(3)
其中,
(4)
1.2 拟声波近似及其控制方程
严格意义上来说,各向异性介质的声波不存在。但对于构造成像来说,与各向同性介质相类似,我们需要一个代表各向异性介质中P波运动学特征的声学近似,就能进行P波波场的外推和成像。声学近似的意义在于用标量场描述各向异性介质中的波场,不用外推矢量波的方程组,大大减少了计算量,这在逆时偏移中十分重要;并且P波控制方程能很好地逼近实际介质中P波分量的运动学特征,能保证构造成像的精确性;不用进行波场分离,就能较好地解决P波和S波耦合的问题,使得P波成像不受S波的干扰。
ALKHALIFAH[25]首先提出了拟声波近似这一概念,在耦合的频散关系中令垂直方向上SV波速度为0,简化了频散关系,从而在运动学上很好地近似描述P波分量,简化出可解的qP波控制方程。
二维情况下,求解Christoffel方程,并代入Thomsen参数,得到不同极化类型波的相速度公式:
(5)
式中:θ是相角;“±”中“+”代表qP波,“-”代表qSV波。
利用耦合的频散作近似,将(5)式两边平方,经过整理,得到qP-qSV波耦合的频散关系:
(6)
式中:kz是纵向波数;vnmo是动校正速度;ω是圆频率;kx和ky分别是x方向和y方向的波数;η代表非椭圆率。
(6)式两边同时乘上f-k域的波场F(kx,ky,kz,ω),反变换到时间域得到最终控制方程:
(7)
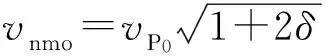
(8)
引入辅助变量:
(9)
(8)式两边乘以p(ω,kx,ky,kz)后可以写作:
(10)
联立(9)式、(10)式,反变换到时间域,得到控制方程:
(11)

1.3 从VTI介质推广到TTI介质
从VTI介质到TTI介质,并没有引入新的波现象,但是会使得控制方程变得更为复杂,也就是引入了更多的交叉导数项,对(11)式进行坐标旋转,可以得到TTI介质的控制方程。在二维情况下,(11)式推广到TTI介质后,变为:
(12)
其中,

(13)
式中:θ0代表地层倾角。
1.4 基于TTI介质的有限差分逆时偏移算子
利用二阶中心差分格式近似二阶时间偏导数,从(12)式可以得到如下的差分方程:
(14)
利用高阶空间差分近似可得空间微分表达式为:
sin2θ0L(x)L(z)
(15)
其中,L(x)=∂/∂x,L(y)=∂/∂y,L(z)=∂/∂z。
利用N阶中心差分近似可以得到:
(16)

1.5 拟声波近似下的波场校正
由于拟声波近似采用的是耦合频散关系,令vs0=0是为了简化控制方程,而并不意味着qSV波相速度处处为0(实际上仅仅当相角为0和90°时相速度才为0),因此qP波分量中都会有耦合的qSV波分量,如图1a所示。本文利用椭圆各向异性介质中胀缩震源不产生转化qSV波的特点,对波场进行校正以减小波场中横波分量的影响,波场校正公式为:
(17)
图1b为校正后的波场;图1c为波场校正量。由图1b和图1c可见,经波场校正后,qSV波的能量得到消除,提高了成像质量。

图1 波场校正效果a 校正前原始波场; b 校正后波场; c 波场校正量
2 三维盐丘理论模型测试
为了验证本文方法的正确性,采用经典SEG TTI各向异性盐丘模型进行试算。图2为模型的示意图,Inline和Crossline方向各901个点(间距均为15m),最大深度为5000m(深度间隔为10m)。采集设计33条测线,正演炮数据共有3333炮,每条测线101炮,线间隔为360m,炮间隔120m,每炮301×301道地震数据,道间隔为30m,记录长度为8s,采样间隔为2ms,震源和检波点埋置在地下10m的位置。

图2 经典SEG TTI各向异性盐丘模型
图3和图4分别是Inline251线的各向异性参数场和RTM深度偏移剖面;图5和图6分别是Crossline251线的各向异性参数场和RTM深度偏移剖面(图中φ代表地层方位角)。对比偏移剖面可以发现,各向异性RTM偏移剖面品质明显优于各向同性RTM偏移,盐丘边界的刻画、地层之间接触关系更清楚合理。尤其是剖面中红色圆圈标注的断层区域,各向异性RTM成像结果断层归位更准确;剖面深层红色方框内的水平同相轴,结果也更准确,深度与真实位置更吻合。图7a和图7b分别为各向同性RTM和各向异性RTM获得的共成像点道集。可以看到,各向同性RTM由于忽略了各向异性参数的影响,成像道集在远偏移距处弯曲,而各向异性RTM克服了各向异性的影响,成像道集在各个偏移距位置均拉平,进一步验证了本文TTI各向异性RTM成像技术的有效性。

图3 Inline251线对应的各向异性参数场a vP0; b ε; c δ; d θ0;e φ

图4 Inline251线对应的深度偏移剖面a 各向同性RTM; b 各向异性RTM

图5 Crossline251线对应的各向异性参数场a vP0; b ε; c δ; d θ0; e φ
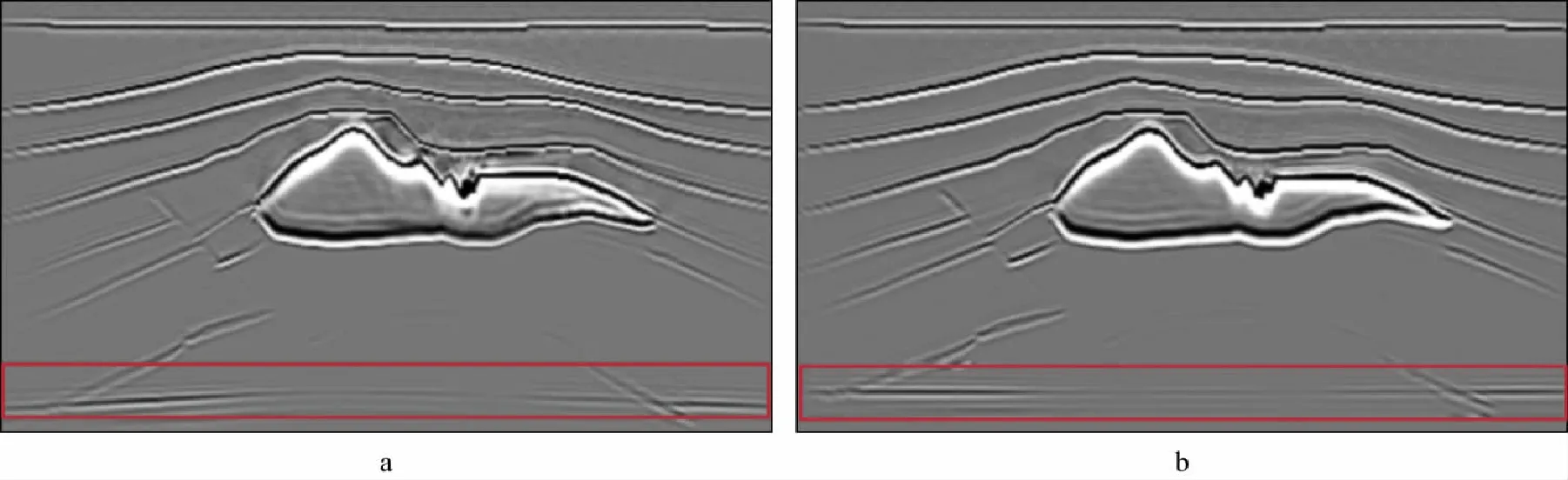
图6 Crossline251线对应的深度偏移剖面a 各向同性RTM; b 各向异性RTM

图7 各向同性RTM(a)和各向异性RTM(b)得到的共成像点道集
3 实际资料处理
为了进一步验证本文方法的有效性和适用性,利用本文提出的TTI各向异性RTM技术对A区151km2实际资料进行了偏移成像处理。图8为偏移所用的TTI各向异性参数模型,由TTI各向异性参数精细建模得到。首先结合测井数据和实际资料采用时差相似性分析等方法建立深度域初始模型,再采用TTI介质层析迭代反演方法建立vP0,ε和δ深度域精细模型;然后在成像剖面上扫描地层倾角和方位角,通过正交关系计算得到对称轴的倾角和方位角模型。这5种TTI介质各向异性参数都影响最终的偏移成像结果,具体表现为:vP0影响最大,主要影响剖面总体成像质量、构造形态、成像深度等;ε影响次之,主要影响大偏移距道集、剖面的聚焦程度、连续程度、构造的水平成像位置等;δ影响非常小,主要影响剩余成像深度等;对称轴倾角和方位角的影响跟地层倾角有关,当地层倾角较大时影响较大,主要影响射线追踪的路径和旅行时。
图9和图10分别给出了Inline201线和Crossline101线采用不同方法得到的偏移剖面。图9a和图10a分别为前期各向同性叠前时间偏移(PSTM)得到的老剖面,分析认为:老剖面整体品质较高,一些大套地层成像较好,但浅层成像信噪比偏低,成像模糊;中深层分辨率偏低,断层成像不清晰;且由于该区存在较强烈的TTI各向异性,成像剖面与测井资料存在较大深度误差(平均80m,最大接近140m),从而对后续的地震资料解释带来较大的困扰。图9b和图10b分别为各向同性RTM成像剖面。与常规PSTM成像结果相比,RTM成像剖面品质更高,信噪比和分辨率都有不同程度的提高,浅层成像更加清晰,中深层断层成像更加清楚,地层之间的接触关系更加合理;井震误差有一定程度改善,但仍然存在较大误差,尤其是构造侧翼误差更大,对解释结果带来较大影响。图9c和图10c分别为各向异性RTM成像剖面,可以看到目的层位与测井分层数据之间几乎没有明显的深度差,与测井数据的匹配更加准确。图11为3种偏移方法成像剖面的井震误差统计图,表1为对应的15口井误差统计表。可以看到,无论是提供井(表1中玫红底色)还是验证井(表1中白色底色),TTI-RTM的井震误差都得到有效控制(平均10m),验证了本文方法在实际资料应用中的有效性和适用性。

图8 TTI偏移各向异性参数模型a vP0模型; b ε模型; c δ模型; d 对称轴倾角模型; e 对称轴方位角模型
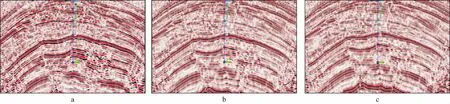
图9 Inline201线偏移剖面对比a 各向同性PSTM; b 各向同性RTM; c TTI各向异性RTM

图10 Crossline101线偏移剖面对比a 各向同性PSTM; b 各向同性RTM; c TTI各向异性RTM

表1 3种偏移方法对应每口井的误差 单位:m

图11 井位置(a)与3种偏移方法的误差(b)
4 认识与结论
本文采用拟声波近似方法推导了VTI各向异性伪声波控制方程,以描述VTI介质地震波传播规律;引入交叉导数项通过坐标旋转得到了对称轴倾斜的TTI各向异性伪声波控制方程;采用高阶有限差分方法推导了TTI各向异性RTM偏移算子。由于采用的是耦合频散关系,令横波速度为0,无法完全消除对成像结果的影响,采用声波近似下的波场校正可以完全消除耦合横波分量,不影响横波成分,提高了TTI各向异性RTM偏移算子的精度。
模型试算和实际资料成像结果表明,本文研究的TTI各向异性RTM成像技术在提高高陡构造、断层和深层盐下构造的成像精度,尤其是消除各向异性引起的成像深度误差方面具有明显的效果。
[1] 张千祥,王德利,周进举.二维TTI介质的纯P波波动方程数值模拟[J].石油物探,2015,54(5):485-492 ZHANG Q X,WANG D L,ZHOU J J.Acoustic wave equation numerical simulation for pure P-wave in 2D TTI medium[J].Geophysical Prospecting for Petroleum,2015,54(5):485-492
[2] 秦海旭,吴国忱.TTI介质弹性波随机边界逆时偏移的实现[J].石油物探,2014,53(5):570-578 QIN H X,WU G C.The implementation of elastic reverse time migration in TTI media based on random boundary[J].Geophysical Prospecting for Petroleum,2014,53(5):570-578
[3] 马光克,李洋森,孙万元,等.可变网格高阶有限差分法逆时偏移研究[J].石油物探,2016,55(5):728-736 MA G K,LI Y S,SUN W Y,et al.Acoustic pre-stack reverse time migration using variable grid finite-difference method[J].Geophysical Prospecting for Petroleum,2016,55(5):728-736
[4] 李振春,李庆洋,黄建平,等.一种稳定的高精度双变网格正演模拟与逆时偏移方法[J].石油物探,2014,53(2):127-136 LI Z C,LI Q Y,HUANG J P,et al.A stable and high-precision dual-variable grid forward modeling and reverse time migration method[J].Geophysical Prospecting for Petroleum,2014,53(2):127-136
[5] 郭书娟,马方正,段心标,等.最小二乘逆时偏移成像方法的实现与应用研究[J].石油物探,2015,54(3):301-308 GUO S J,MA F Z,DUAN X B,et al.Research of least-squares reverse-time migration imaging method and its application[J].Geophysical Prospecting for Petroleum,2015,54(3):301-308
[6] 段新意,李振春,黄建平,等.各向异性介质共炮域高斯束叠前深度偏移[J].石油物探,2014,53(5):579-586 DUAN X Y,LI Z C,HUANG J P,et al.A prestack Gaussian beam depth migration in common-shot domain for anisotropic media[J].Geophysical Prospecting for Petroleum,2014,53(5):579-586
[7] RUDZKI M J P.Über die gestalt elastischer wellen in gesteinen (Ⅱ):studie aus der theorie der erdbebenwellen[J].Anzeiger der Akademie der Wissenschaften Krakau,1897:387-393
[8] GASSMANN F.Elastic waves through a packing of spheres[J].Geophysics,1951,16(4):673-685
[9] LEVIN F K.The reflection,refraction,and diffraction of waves in media with an elliptical velocity dependence[J].Geophysics,1978,43(3):528-537
[10] TSVANKIN I,THOMSEN L.Nonhyperbolic reflection moveout in anisotropic media[J].Geophysics,1994,59(8):1290-1304
[11] SUN C W,MARTINEZ R D.3D Kirchhhoff PS-wave prestack time migration for V(z) and VTI media[J].Expanded Abstracts of 73rdAnnual Internat SEG Mtg,2003:957-960
[12] 周巍,王鹏燕,杨勤勇,等.各向异性克希霍夫叠前深度偏移[J].石油物探,2012,51(5):476-485 ZHOU W,WANG P Y,YANG Q Y,et al.Anisotropy Kirchhoff prestack depth migration[J].Geophysical Prospecting for Petroleum,2012,51(5):476-485
[13] GUO J S,BIONDO B.Plane-wave migration in tilted coordinates[J].Geophysics,2008,73(5):S185-S194
[14] 刘礼农,张剑锋.三维各向异性介质中的波动方程叠前深度偏移方法[J].地球物理学报,2011,54(11):2906-2915 LIU L N,ZHANG J F.Wave equation prestack depth migration method in 3D VTI media[J].Chinese Journal of Geophysics,2011,54(11):2906-2915
[15] 吴国忱,梁锴,王华忠.VTI介质qP波广义高阶屏单程传播算子[J].石油地球物理勘探,2007,42(6):640-650 WU G C,LIANG K,WANG H Z.High-order one-way generalized-screen propagation operator of qP-wave in VTI medium[J].Oil Geophysical Prospecting,2007,42(6):640-650
[16] 梁锴,吴国忱,印兴耀.TTI介质qP波方程频率-空间域加权平均有限差分算子[J].石油地球物理勘探,2007,42(5):516-525 LIANG K,WU G C,YIN X Y.Weighted mean finite-difference operator of qP wave equation in frequency-space domain for TTI medium[J].Oil Geophysical Prospecting,2007,42(5):516-525
[17] ZHU T,GRAY S H,WANG D.Prestack Gaussian-beam depth migration in anisotropic media[J].Geophysics,2007,72(3):S133-S138
[18] 张凯,段新意,李振春,等.角度域各向异性高斯束逆时偏移[J].石油地球物理勘探,2015,50(5):912-918 ZHANG K,DUAN X Y,LI Z C,et al.Angle domain reverse time migration with Gaussian beam in anisotropic media[J].Oil Geophysical Prospecting,2015,50(5):912-918
[19] 王伟国,熊水金,徐华宁,等.TTI介质各向异性伪谱法逆时偏移[J].石油地球物理勘探,2012,47(4):566-572 WANG W G,XIONG S J,XU H N,et al.Reverse-time migration using pseudo-spectral method for tilted TI media[J].Oil Geophysical Prospecting,2012,47(4):566-572
[20] 王娟,李振春,孙小东,等.TTI介质逆时偏移成像[J].石油地球物理勘探,2012,47(4):573-577 WANG J,LI Z C,SUN X D,et al.Reverse time migration in tilt transversely isotropic(TTI) media[J].Oil Geophysical Prospecting,2012,47(4):573-577
[21] FLETCHER R P,DU X,FOWLER P J.Reverse time migration in tilted transversely isotropic(TTI) media[J].Geophysics,2009,74(6):WCA179-WCA187
[22] DU X,BANCROFT J C,LINES L R.Reverse-time migration for tilted TI media[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005:1930-1933
[23] DU X,FLETCHER R,FOWLER P J.A new pseudo-acoustic wave equation for VTI media[J].Expanded Abstracts of 70thEAGE Conference and Exhibition,2008:2082-2086
[24] THOMSEN L.Weak elastic anisotropy[J].Geophysics,1986,51(10):1954-1966
[25] ALKHALIFAH T.An acoustic wave equation for anisotropic media[J].Geophysics,2000,65(4):1239-1250
[26] ZHOU H,ZHANG G,BLOOR R.An anisotropic acoustic wave equation for VTI media[J].Expanded Abstracts of 68thEAGE Conference and Exhibition,2006:H033
(编辑:陈 杰)
Anisotropic reverse time migration technique in TTI media and its application
WANG Xianbin
(SinopecGeophysicalResearchInstitute,Nanjing211103,China)
Anisotropy is widespread in the subsurface formation medium.The conventional isotropic seismic migration imaging technique often leads to low imaging accuracy and even depth error.The application of wide azimuth seismic acquisition technique and high precision RTM imaging technology have highlighted the influence of anisotropy.In this paper we begin with the weakly anisotropic elastic wave equation,First,the VTI anisotropic pseudo acoustic wave control equation is obtained by quasi acoustic approximation.Then,the cross derivative term is introduced to coordinate rotation to get the TTI anisotropic pseudo acoustic wave control equation.Next,the TTI-RTM migration operator is obtained by high order finite difference.Finally,the influence of the S-wave component is eliminated by wave field correction to improve the accuracy of the anisotropic migration operator.The model test and field data processing results show that,the technique is more beneficial to the anisotropic medium with higher precision and it’s an ideal technique for high precision seismic imaging.
anisotropy,quasi acoustic wave approximate,control equation,TTI reverse time migration
2016-12-21;改回日期:2017-03-28。
王咸彬(1965—),男,博士,高级工程师,主要从事地球物理方法技术研究与管理工作。
国家高技术研究发展计划(863计划)项目(2011AA060303)资助。
P631
A
1000-1441(2017)04-0534-09
10.3969/j.issn.1000-1441.2017.04.009
This research is financially supported by the National High-tech R&D Program (863 Program) (Grant No.2011AA060303).

