地震叠前逆时偏移衰减随机边界条件研究

柯 璇,石 颖,2,张莹莹,张 振

(1.东北石油大学地球科学学院,黑龙江大庆163318;2.黑龙江省普通高校科技创新团队“断层变形、封闭性及与流体运移”,黑龙江大庆163318;3.中国石油塔里木油田分公司勘探开发研究院,新疆库尔勒841000)

地震叠前逆时偏移衰减随机边界条件研究

柯 璇1,石 颖1,2,张莹莹1,张 振3

(1.东北石油大学地球科学学院,黑龙江大庆163318;2.黑龙江省普通高校科技创新团队“断层变形、封闭性及与流体运移”,黑龙江大庆163318;3.中国石油塔里木油田分公司勘探开发研究院,新疆库尔勒841000)

逆时偏移的边界条件及存储需求往往相互制约,二者的选取直接影响逆时偏移的成像结果和适用条件,因此对逆时偏移边界条件和对应存储策略的研究具有重要意义。提出了一种衰减随机边界条件,在真实波场外围依次加入衰减层和随机速度层,可有效降低随机反射对真实波场的能量干扰。对波动方程逆向运算重建激发点波场,结合互相关成像条件,完成逆时偏移计算。对比分析随机边界条件、完全匹配层边界条件和衰减随机边界条件的测试结果,与随机边界条件相比,衰减随机边界条件在牺牲较少存储效率的情况下,能够获得接近吸收边界条件的偏移效果。盐丘模型和大偏移距模型算例分析结果验证了以上结论的正确性。

逆时偏移;随机边界;存储;波场重建

逆时偏移[1]对复杂构造成像具有良好的效果,因此成为地球物理研究的热点之一[2-5]。而计算精度的提高和波场存储需求的降低则一直是逆时偏移算法的重要研究方向。计算精度方面,除提升波场模拟精度外,还需要采用适合的边界条件压制边界反射,削弱干扰噪声。BÉRENGER[6]提出了完全匹配层(Perfectly Matched Layer,PML)边界条件,在波场外侧设置衰减层并引入衰减因子,在衰减层内采用带衰减项的波动方程进行波场递推计算,进而达到消除边界反射的目的,该方法易于实现且吸收效果较好[7-12]。张衡等[13]提出了VTI介质非分裂式PML吸收边界条件,人工反射吸收效率得到明显提高。LIU等[14]提出一种混合边界条件,衰减层内的波场计算由双程波方程逐渐转化为单程波方程,再对波场进行衰减吸收,该方法所需吸收层数较少,间接降低了波场的计算量和存储量。在逆时偏移算法中,由于激发点和检波点波场往往需进行同时刻互相关计算,但全波场保存的存储量占用在实际应用中难以实现,因此,逆时偏移的存储需求成为限制逆时偏移发展的瓶颈之一。对此,SYMES[15]设置了检查点存储临时波场,节省了存储空间,但需引入额外计算量用于波场重建;FENG等[16]提出一种波场存储方法,存储边界处的单层波场及最后两时刻的全波场,采用变阶数有限差分算法进行波场重建,但由于缺少准确的边界波场,这种方法在波场反传时会引入误差。CLAPP[17]提出了一种吸收边界条件下的波场存储策略,根据有限差分阶数保存若干层波场,可保证重建波场无精度损耗。但是该方法需进行频繁的数据交换,尤其是在对逆时偏移算法应用GPU加速时[18-20],计算硬件之间频繁的数据传输会导致较大的时间延迟,不利于提高计算效率;王保利等[21]针对该方法提出了一种有效边界存储策略,并将其应用于GPU加速平台,引入检查点思想,进一步降低了数据存储量,结合GPU高性能计算的优势,在保证波场重建精度的同时,计算耗时也得到良好的控制。

吸收边界条件虽然可以压制边界反射干扰,但往往需要进行大量的波场存储,CLAPP[22]提出的随机边界条件,在速度场外围引入随机速度层,降低了边界反射的相关性,从而以随机噪声的形式保存了波场能量,对原方程进行逆向运算,即可获得历史波场,仅需保存最后两时刻波场切片,所需存储量较少。然而,随机噪声是初至波场直接经由随机速度层反射而来,其能量往往与有效反射波场的能量处于同一量级,会在偏移剖面上产生较大的影响。SHEN等[23]提出一种改进的随机边界条件,对低频波场的随机散射效率更高,更有利于进行波形反演计算,但仍无法解决随机反射的干扰问题。综上所述,目前关于逆时偏移的边界条件和存储策略的研究均为针对解决边界噪声和波场存储量二者当中的一个问题,并没有一个更灵活的折中方案。

本文方法综合运用PML边界条件和随机边界条件,旨在保证逆时偏移成像精度的基础上,降低波场存储空间。边界条件方面,在真实波场外围依次加入衰减层和随机速度层,降低随机反射波振幅,从而减少随机噪声对逆时偏移结果的影响。存储策略方面,与随机边界条件的存储策略类似,保存最后时刻波场,采用波动方程的逆向运算重建激发点波场信息,进而与接收点波场完成互相关计算,实现逆时偏移成像。在此基础上,本文方法需设置检查点,保存临时波场,以降低波场重建过程中的累积误差。最后,对盐丘模型和大偏移距模型进行逆时偏移试算,验证了本文方法的有效性。

1 衰减随机边界条件

根据逆时偏移的算法需求,在进行地震数据偏移成像过程中,需获得历史时刻激发点波场信息,但保存全部激发点波场信息会消耗巨大的存储空间[18],为节约数据存储空间,研究人员常使用CLAPP提出的随机边界条件[22],该方法在有效速度场外加入随机速度场,不进行边界处波场能量的吸收,然后根据波动方程进行反向运算即可构建历史波场。但是由于初至波场能量较强,入射至随机边界层后,产生的随机反射会形成强能量干扰,往往会在偏移剖面上形成较强的虚假同相轴。我们结合随机边界条件思想,提出一种速度场的构建方法:首先在有效速度场(图1 中区域a)外进行速度等效拉伸(图1中区域b),然后在外层加入随机速度场(图1中区域c)。逆时偏移算法中,后续的波场模拟计算,即采用上述方法构建的速度场。

图1 随机边界速度场

逆时偏移算法可采用声波波动方程进行波场模拟,在二维空间内,假定密度为常数,通常采用(1)式所示的声波方程进行数值计算:

(1)

式中:P(x,z,t)为地震波场;V(x,z)为地下介质速度;x和z分别为空间水平方向和垂直方向的坐标;t为时间。

本文采用PML吸收方程进行波场计算[12]:

(2)

式中:A(x,z)为衰减系数矩阵,衰减系数值随边界层外法线方向呈递增趋势分布,可通过线性函数、指数函数和三角函数等方法进行构建[10-12]。当A(x,z)为0时,方程(2)可化简为(1)式所示的声波波动方程。

本文方法在速度等效拉伸区域(图1中区域b)构建衰减系数,当波场入射至此区域时,产生能量衰减,其余区域衰减系数设置为0,无振幅衰减,即(2)式中A(x,z)项为0,波场的传播遵循(1)式。

本文采用有限差分数值方法对方程(2)进行离散,整理可得如下形式:

(3)

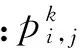
应用方程(3)可进行激发点波场的正向传播模拟,且当地震波进入边界吸收层后,其振幅会逐渐衰减。

2 波场重建

(4)

应用方程(4)可实现激发点波场的逆时传播,当衰减系数di,j为0时,激发点波场无振幅衰减,当di,j为非零值时,即在正传波场的衰减区域,地震波振幅会逐渐增强。

对利用方程(3)计算得到的正传波场,仅保存最后两时刻激发点波场,由方程(4)进行激发点波场的逆时重建,再对其同接收点波场应用互相关成像条件,即可完成逆时偏移成像。

为验证本文方法对随机噪声的衰减作用,分别利用随机边界条件和衰减随机边界条件进行地震波场的正传模拟和重建实验。模型大小为301×301个网格点,网格间距为8m,设置50层边界,其中内侧40层做速度等效拉伸,最外侧的10层为随机速度层。采用衰减随机边界条件时,边界层内侧40层为吸收层,设置衰减因子。假定模型为3500m/s的匀速介质,震源位于模型的中央位置,震源子波为主频30Hz的雷克子波,时间采样率为0.5ms,波场传播最大时刻为0.55s,采用两种边界条件计算的地震波场在0.55s的波场快照如图2所示。

抽取1.2km深度处(图2中虚线位置)波场数据可见,假定地震子波最大振幅为10000时,在有效波场范围内(0.4～2.0km),采用随机边界条件在虚线处产生的随机噪声最大振幅值为2588,如图3中虚线所示;采用衰减随机边界条件,由于随机噪声需经过衰减层传播,进入有效波场区域的随机噪声得以衰减,最大振幅值为669,如图3中实线所示。由此可知,采用衰减随机边界条件,经过衰减层后,随机反射噪声被有效压制,振幅强度下降明显。

为验证本文方法波场重建的准确性,进行了地震波场的重建实验,并在同参数条件下,与随机边界条件的波场重建结果进行了对比。图4a和图4b分别为采用衰减随机边界条件在0.25s时刻波场快照和波场传至0.55s后,反传至0.25s时的波场快照,可以看出,正、反传波场无明显差异,抽取1.2km深度处的波场数据进行对比(图5)可以看出,二者振幅无明显差异。

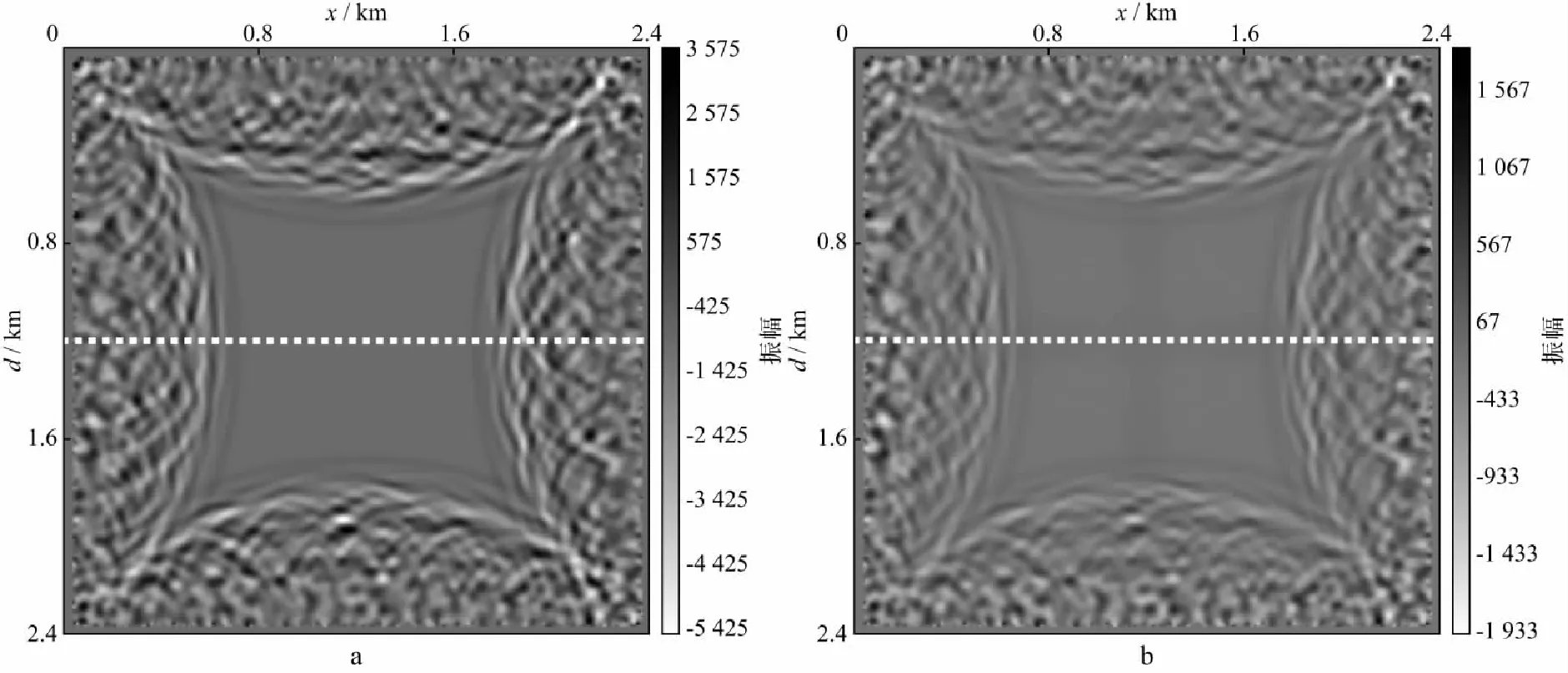
图2 不同边界条件波场快照对比(t=0.55s)a 随机边界条件; b 衰减随机边界条件

图3 随机边界条件与衰减随机边界条件随机噪声振幅对比

图4 衰减随机边界条件正传与反传波场快照对比(t=0.25s)a 正传波场快照; b 反传波场快照

图6a和图6b分别为随机边界条件下0.25s时刻波场快照和波场传至0.55s后,再反传至0.25s时的波场快照。由图6可见,二者并无明显差别。进一步抽取1.2km处的波场数据进行对比,如图7所示,二者振幅大小相当。

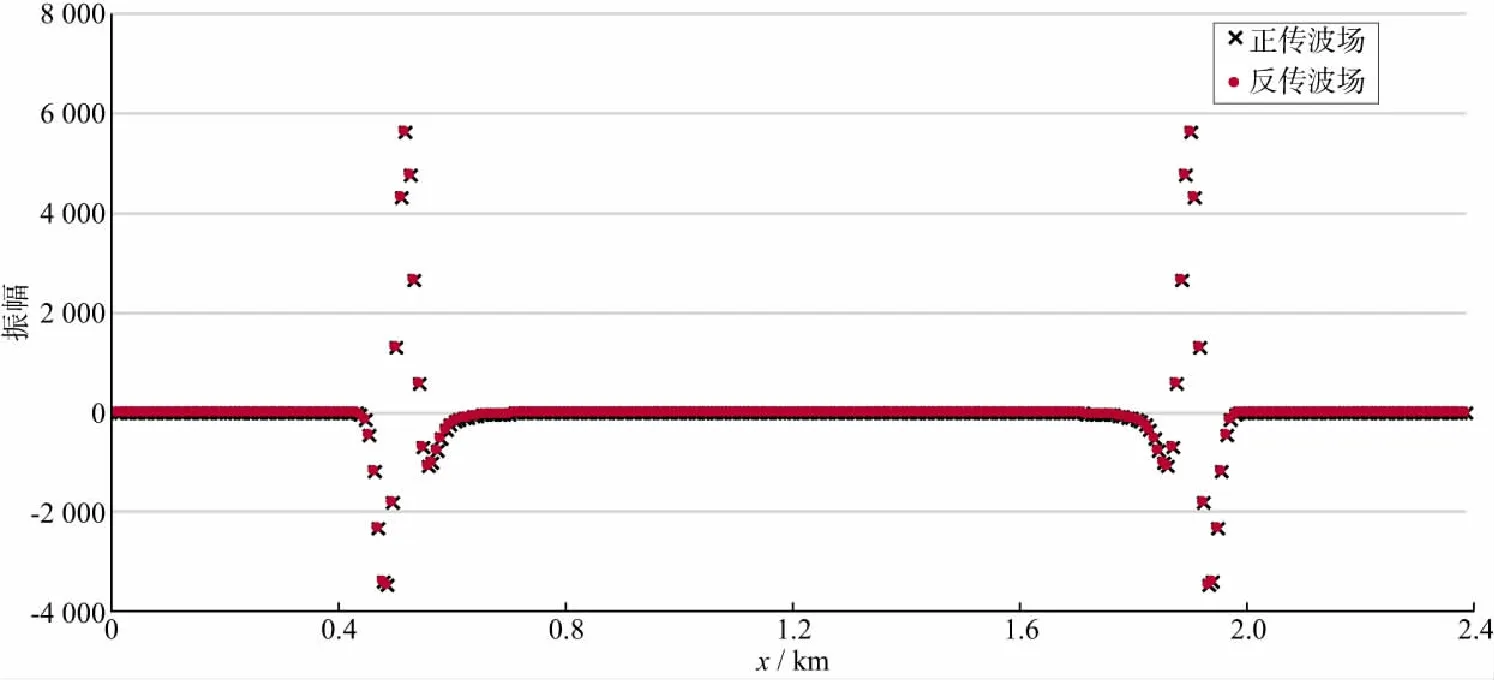
图5 图4a和图4b所示波场在1.2km处振幅对比

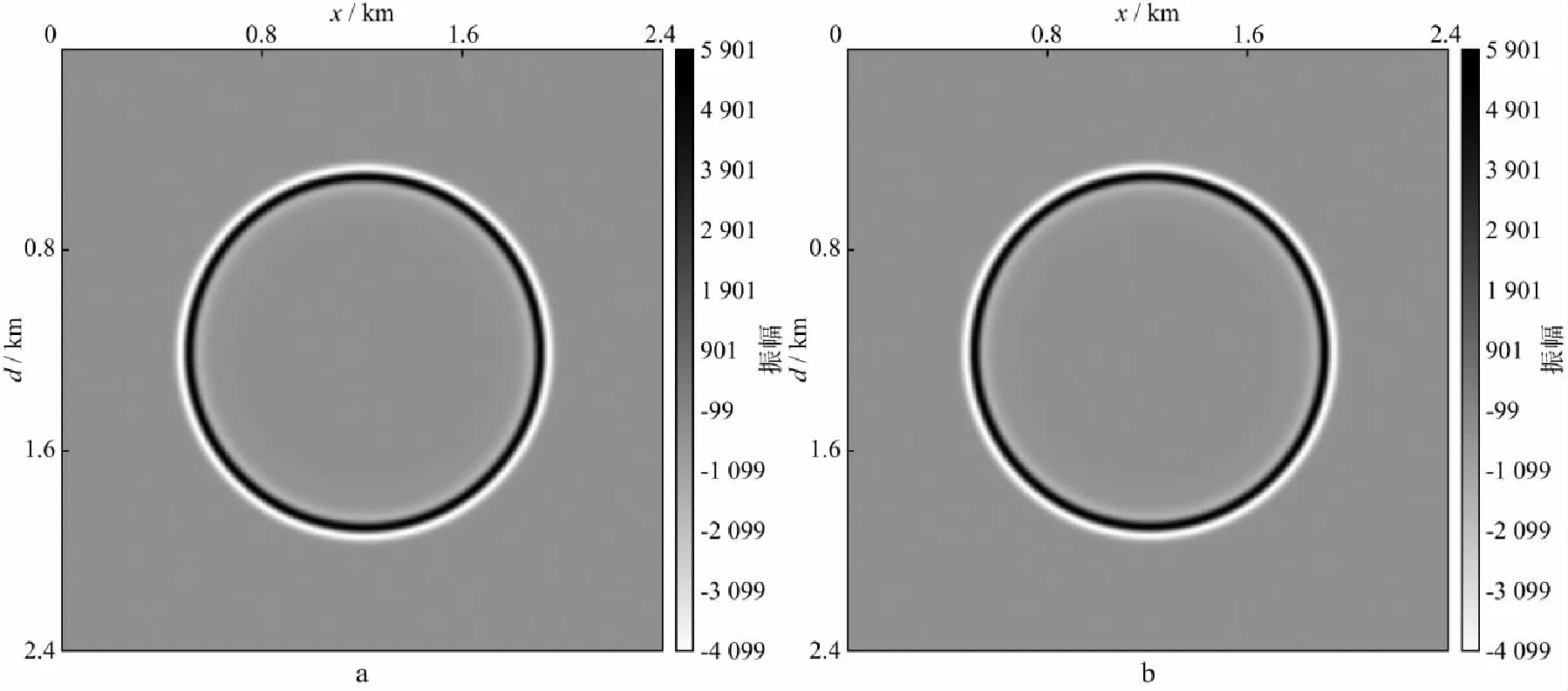
图6 随机边界条件正传与反传波场快照对比(0.25s)a 正传波场快照; b 反传波场快照

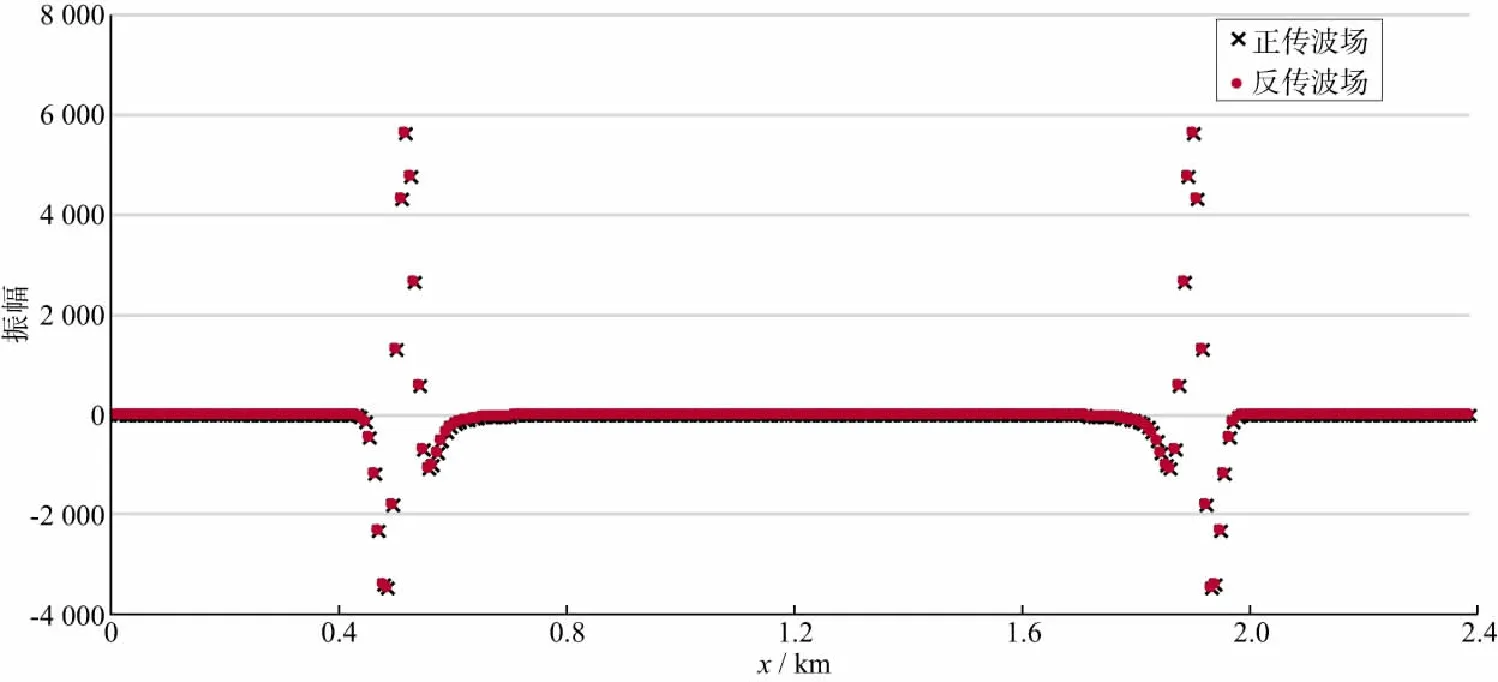
图7 图6a和图6b所示波场在1.2km处振幅对比

为了进行误差的量化对比,分别对两种边界条件的正、反传波场进行了差剖面测试。图8a为采用随机边界条件在0.25s时刻正、反传波场的差剖面,最大误差值为0.023,图8b为采用衰减随机边界条件在0.25s时刻正、反传波场的差剖面,最大误差值为0.310。可以看出,应用衰减随机边界条件进行波场恢复所产生的误差值虽然较随机边界条件更大,但误差主要分布在衰减层区域，对有效成像区域的影响可忽略。主要原因在于:当波场进入衰减区后,随着波场的传播,振幅衰减程度逐渐增大,采用本文方法进行波场重建时,会有部分波场由于振幅过小而无法完全得到保真恢复,进而产生波场畸变[17]。本文方法虽然在衰减区引入了部分误差，但与对随机噪声的衰减效果相比，波场的整体噪声水平有所下降。

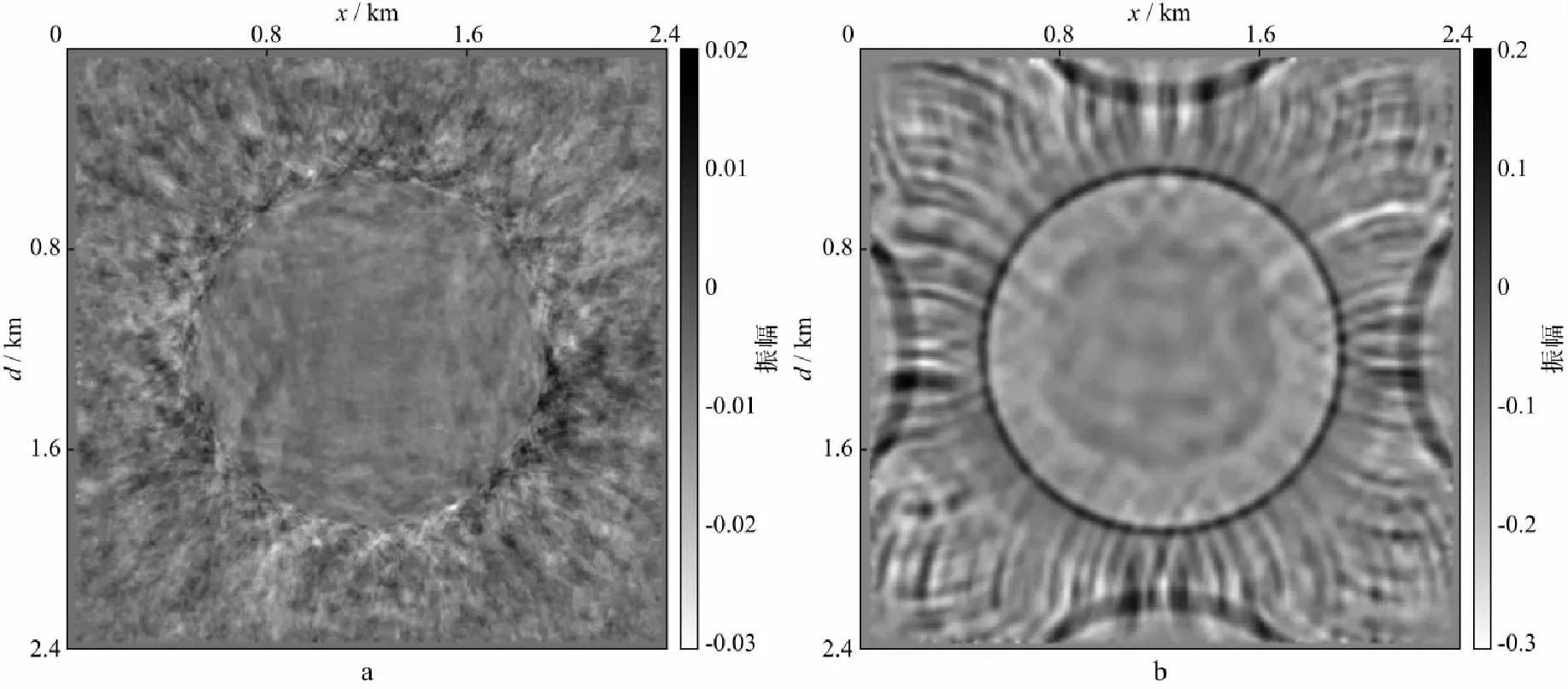
图8 不同边界条件正传与反传波场误差对比(t=0.25s)a 随机边界条件; b 衰减随机边界条件

保存波场的时间周期的选取,受衰减系数影响,可根据正传波场与反传波场之间的一致性选择波场保存周期。

本文采用公式(5)进行波场一致性估算:

(5)

式中:pf(i,j)为正传波场;pb(i,j)为反传重建波场;I,J为空间水平、垂直方向网格点数;i,j为空间坐标;Eτ为两种波场的一致性。公式(5)实质上是估算每个网格点上正传波场、反传波场的能量差异与正传波场能量的平均比值,可间接反映误差对真实波场的影响程度。

图9显示了当Eτ不超过0.2时,波场迭代时间随衰减系数的变化趋势。当衰减矩阵中最大衰减系数小于30时,由于衰减程度较弱,振幅恢复较准确,更接近于随机边界条件,波场持续时间均接近于本次实验最大采样时间。随着衰减系数的增大,重建波场在满足精度要求的基础上，迭代时间下降。考虑到实际应用时对噪声影响和波场存储量的需求,建议最大衰减系数选取20～30,既可保证对随机噪声的衰减,又能增加迭代时间，减少检查点个数，控制波场存储量。

3 存储量分析

波场存储量和计算量是评判逆时偏移边界条件和存储策略的重要指标,本文对比分析了随机边界条件、衰减随机边界条件和PML吸收边界条件的计算量和存储量。

如前所述，索绪尔从未提及语言本体论，自然不可能指出本体及其属性是其理论推理的基点，但他却将“任意性作为构造理论的第一原理或公理，其他论断则由此演绎出来” [35]21。那么，任意性和本体是什么关系呢？“任意性原则之所以是‘头等重要的’，在于它集中地反映了索绪尔语言学的本体论特征，它充分地说明了语言实体的本原性” [36]54。这也就是说，任意性是本体的根本属性。索绪尔虽然没有明确提及本体论，但他特别强调任意性，并把它高调定位为语言学的第一原则，实质上也就确立了本体论的基础地位。

设定模型水平方向网格点数为Nx,垂直方向的网格点数为Nz,边界层数为L,空间差分阶数为2K,波场传播在时间方向的采样点数为T,每隔C个时间点进行一次临时波场存储,为便于统计,假设Nx=Nz=N，则二维空间内,随机边界条件的存储需求为2(N+2L)2·4字节,衰减随机边界条件的存储需求为2T·(N+2L)2·4/C字节,采用PML吸收边界条件及有效边界存储策略的存储需求为4KNT·4字节,易知通常情况下PML吸收边界条件存储量占用最大,衰减随机边界条件次之,随机边界条件的存储需求最小。

在波场反传过程中,需要对整体波场进行计算,但由于衰减随机边界条件采用带有衰减项的波动方程,因此在网格点数相同的情况下,衰减随机边界条件的计算量略大于随机边界条件,由于PML吸收边界条件在波场反传过程中并非全波场计算,因此无法进行计算量的量化对比。

4 逆时偏移算例

为验证本文方法在逆时偏移应用中的有效性,分别采用随机边界条件、PML边界条件(有效边界存储策略)和衰减随机边界条件进行逆时偏移计算。

测试的模型水平方向网格点数为800、垂直方向网格点数为600,空间网格间距为10m,激发100炮,炮点位于0～8000m,炮间距80m,接收点位于地表0～8000m,共800个检波器,道间距10m,时间采样间隔为0.8ms,采样点数为6000,共记录4.8s,成像条件为震源归一化互相关成像条件。

4.1 随机边界条件

考虑到常规声波波动方程无振幅能量衰减的特性,随机边界条件[22]在速度场外围加入随机速度层,当波场传播至随机速度层后,并不会产生衰减,即波场能量并无损失,而是以随机散射噪声的形式得以保存。因此,理论上对随机边界条件下的任意时刻波场,采用波动方程的逆向运算,即可获得历史波场。在逆时偏移应用中,保存最大时刻的激发点波场信息,根据原波动方程即可实现激发点波场的逆时反传,从而与检波点波场进行相关成像。

本文测试设定边界层数为100,外侧30层为随机速度层,内侧70层根据模型速度场做等效拉伸。存储策略为保存最后两时刻激发点波场,同时进行激发点波场反传和接收点波场正传,完成逆时偏移成像。

4.2 PML吸收边界条件(有效边界存储策略)

PML吸收边界条件[6]通过修改波动方程,引入衰减项,当波场进入边界层后,会由内向外逐渐衰减,且不会产生剧烈反射。该边界条件可有效解决波场的边界反射问题,但由于在边界层内,波场振幅被衰减,所以常规的波动方程逆向运算无法精确重建激发点波场。有效边界存储策略是根据有限差分法中空间差分的计算特性,在激发点波场正传时,保存一定层数的内部波场,从而进行波场逆推,理论上,层数为空间差分阶数的一半时,即可实现波场的精确重建[21]。

本文测试设定边界层数为100,边界层内为PML吸收边界条件,在激发点波场正传过程中,根据本文采用的10阶空间差分,保存5层边界波场及最后两时刻波场;在激发点波场反传过程中,每时刻均在有效边界层中进行波场加载,保证内部有效区域内的波场信息完整。理论上,该方法对有效区域内激发点波场的恢复精度最高,等同于保存全部波场所获得的计算精度,因此在本文中,将采用该方法的逆时偏移剖面作为评判偏移效果的参考。

4.3 衰减随机边界条件(检查点存储策略)

边界层数为100,外侧30层为随机速度层,对波场无衰减;内侧70层根据模型速度场做等效拉伸且设置PML衰减层。存储策略方面,根据检查点间隔,每隔一定时间进行一次波场保存,本次测试检查点设置为600,即每隔600个时间点保存一次波场。在运用方程(4)进行激发点波场反传过程中,当传播至检查点时刻时,用保存的波场进行波场替换,然后继续反传。

图10给出了速度模型及采用不同边界条件得到的偏移剖面。由图10可见,采用随机边界条件的偏移剖面,受随机噪声影响较大,在中浅层由于入射至边界层的波场能量较强,因此随机噪声影响较为明显,出现了杂乱的同相轴,影响对真实构造形态的判断;采用衰减随机边界条件与PML边界条件的偏移剖面无明显差异。在本文逆时偏移测试中,PML吸收边界条件波场存储量约为320.4MB,衰减随机边界条件(检查点间隔为600)波场存储量仅约为54.9MB,较前者节约了5倍存储量,随机边界条件波场存储量占用最小,约为6.1MB,实验结果与本文第3部分结论一致,3种边界条件的波场存储量及噪声影响情况如表1所示。

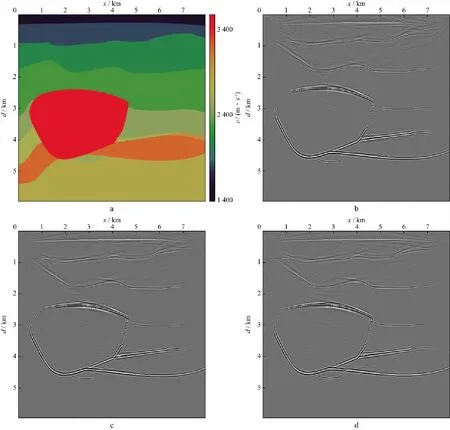
图10 速度模型及采用不同边界条件得到的逆时偏移剖面a 速度模型; b 随机边界条件; c PML吸收边界条件; d 衰减随机边界条件

边界条件及存储策略波场存储量噪声影响随机边界条件小大衰减随机边界条件中小PML吸收边界条件(有效边界存储策略)大小

4.4 大偏移距模型测试

在横纵比较大的模型中,为完成远偏移距炮集数据的成像计算,通常采用较大的采样时长,即逆时偏移的时间采样时长远超过近偏移距数据的成像时长,从而能更全面地测试近偏移距区域边界条件的应用效果。为进一步检测衰减随机边界条件的适用性,本文进行了大偏移距模型的逆时偏移测试。测试模型水平方向网格点数为1501,垂直方向网格点数为151,横纵比约为10∶1,边界层数为100,3种边界条件的设置与4.1到4.3节一致。水平和垂直方向的空间网格间距为10m,精确速度模型如图11a所示,逆时偏移所用的平滑速度模型如图11b所示。激发11炮,炮点位于4000～10000m,炮间距600m,接收点位于地表0～15000m,共1501个检波器,道间距10m,时间采样间隔为1.0ms,采样点数为5000,共记录5.0s,成像条件为互相关成像条件。

图11c到图11e分别为随机边界条件、PML边界条件(有效边界存储策略)和衰减随机边界条件(检查点间隔为600)的逆时偏移测试结果。对比可知,在该模型测试中,采用随机边界条件时,逆时偏移剖面仍存在较大的随机噪声干扰;采用PML边界条件和本文提出的衰减随机边界条件的结果相近,无随机噪声干扰。

由于远偏移距数据受覆盖次数限制和折射波影响,逆时偏移效果不尽理想,因此本文在逆时偏移叠加成像过程中,对远偏移距的成像结果进行了衰减,分别采用上述3种边界条件得到的测试结果如图11f到图11h所示。对比可知,经远偏移距成像数据衰减后,采用3种边界条件的逆时偏移结果得到明显改善,同时也可发现,采用随机边界条件仍存在随机噪声干扰;采用PML边界条件和衰减随机边界条件得到的结果则不存在随机噪声干扰。

图11 速度模型及不同边界条件逆时偏移和远偏移距衰减逆时偏移剖面a 精确速度模型; b 平滑速度模型; c 随机边界条件逆时偏移剖面; d PML边界条件逆时偏移剖面; e 衰减随机边界条件逆时偏移剖面; f 随机边界条件远偏移距衰减逆时偏移剖面; g PML吸收边界条件远偏移距衰减逆时偏移剖面; h 衰减随机边界条件远偏移距衰减逆时偏移剖面

本节测试中,随机边界条件存储量占用约为2.27MB,PML吸收边界条件波场存储量约为315.09MB,衰减随机边界条件(检查点点数为600)波场存储量约为38.0MB,进一步验证了本文方法在保证成像精度的基础上,降低了波场存储量。

5 结论与展望

本文方法综合利用了随机边界条件对反射波场随机化的特性和吸收边界条件对波场振幅的衰减特性,在随机速度层内侧加入波场衰减层,对随机反射波场进行衰减,从而降低随机噪声干扰,并且通过对波动方程的逆向运算重建激发点波场,降低逆时偏移过程中波场的存储量。对于波场重建过程中产生的波形畸变,结合检查点波场存储策略可将其有效压制。模型数据逆时偏移试算表明,本文方法能够在牺牲较小存储效率的基础上,有效压制随机噪声的影响。

相比于随机边界条件方法,本文方法存在一定不足,例如计算量略大,而且因需要在检查点时间处进行波场保存,会带来额外的波场存储量和数据传输延迟。

相比于PML吸收边界条件及其存储策略,本文方法波场存储需求较小。而且由于具有较高的成像精度,噪声引入少,因此本文方法同样适用于最小二乘逆时偏移及全波形反演等算法中的梯度计算,这也是作者下一步的研究工作。

[1] BAYSAL E,KOSLOFF D D,SHERWOOD J W C.Reverse time migration[J].Geophysics,1983,48(11):1514-1524

[2] 杨勤勇,段心标.逆时偏移技术发展现状与趋势[J].石油物探,2010,49(1):92-98 YANG Q Y,DUAN X B.Development status and trend of reverse time migration[J].Geophysical Prospecting for Petroleum,2010,49(1):92-98

[3] 毕丽飞,秦宁,杨晓东,等.弹性多波高斯束逆时偏移方法[J].石油物探,2015,54(1):64-70 BI L F,QIN N,YANG X D,et al.Gauss beam reverse time migration method for elastic multiple wave[J].Geophysical Prospecting for Petroleum,2015,54(1):64-70

[4] 郭书娟,马方正,段心标,等.最小二乘逆时偏移成像方法的实现与应用研究[J].石油物探,2015,54(3):301-308 GUO S J,MA F Z,DUAN X B,et al.Research of least-squares reverse-time migration imaging method and its application[J].Geophysical Prospecting for Petroleum,2015,54(3):301-308

[5] 段心标,王华忠,白英哲,等.基于GPU的三维起伏地表单程波叠前深度偏移[J].石油物探,2016,55(2):223-230 DUAN X B,WANG H Z,BAI Y Z,et al.3D one-way wave equation prestack depth migration from topography based on the acceleration of GPU[J].Geophysical Prospecting for Petroleum,2016,55(2):223-230

[6] BÉRENGER J P.A perfectly matched layer for the absorption of electromagnetic waves[J].Journal of Computational Physics,1994,114(2):185-200

[7] WENG C C,WEEDON W H.A 3D perfectly matched medium from modified maxwell’s equations with stretched coordinates[J].Microwave & Optical Technology Letters,1994,7(13):599-604

[8] 吴国忱,梁锴.VTI介质准P波频率空间域组合边界条件研究[J].石油物探,2005,44(4):301-307 WU G C,LIANG K.Combined boundary conditions of quasi-P wave within frequency-space domain in VTI media[J].Geophysical Prospecting for Petroleum,2005,44(4):301-307

[9] 单启铜,乐友喜.PML边界条件下二维粘弹性介质波场模拟[J].石油物探,2007,46(2):126-130 SHAN Q T,YUE Y X.Wavefield simulation of 2-D viscoelastic medium in perfectly matched layer boundary[J].Geophysical Prospecting for Petroleum,2007,46(2):126-130

[10] 陈可洋.完全匹配层吸收边界条件研究[J].石油物探,2010,49(5):472-477 CHEN K Y.Study on perfectly matched layer absorbing boundary condition[J].Geophysical Prospecting for Petroleum,2010,49(5):472-477

[11] 高刚,贺振华,黄德济,等.完全匹配层人工边界条件中的衰减因子分析[J].石油物探,2011,50(5):430-433 GAO G,HE Z H,HUANG D J,et al.Analysis on attenuation factor in the processing of artificial boundary conditions of PML[J].Geophysical Prospecting for Petroleum,2011,50(5):430-433

[12] 王维红,柯璇,裴江云.完全匹配层吸收边界条件应用研究[J].地球物理学进展,2013,28(5):2508-2514 WANG W H,KE X,PEI J Y.Application investigation of perfectly matched layer absorbing boundary condition[J].Progress in Geophysics,2013,28(5):2508-2514

[13] 张衡,刘洪,李博,等.VTI介质声波方程非分裂式PML吸收边界条件研究[J].石油物探,2016,55(6):781-792 ZHANG H,LIU H,LI B,et al.The research on unsplit PML absorbing boundary conditions of acoustic equation for VTI media[J].Geophysical Prospecting for Petroleum,2016,55(6):781-792

[14] LIU Y,SEN M K.A hybrid scheme for absorbing edge reflections in numerical modeling of wave propagation[J].Geophysics,2010,75(2):A1-A6

[15] SYMES W W.Reverse time migration with optimal checkpointing[J].Geophysics,2007,72(5):213-221

[16] FENG B,WANG H Z.Reverse time migration with source wavefield reconstruction strategy[J].Journal of Geophysics & Engineering,2012,9(1):69-74

[17] CLAPP R G.Reverse time migration:saving the boundaries[R].Stanford Exploration Project,2008:136-144

[18] 李博,刘红伟,刘国峰,等.地震叠前逆时偏移算法的CPU/GPU实施对策[J].地球物理学报,2010,53(12):2938-2943 LI B,LIU H W,LIU G F,et al.Computational strategy of seismic pre-stack reverse time migration on CPU/GPU[J].Chinese Journal of Geophysics,2010,53(12):2938-2943

[19] 刘红伟,李博,刘洪,等.地震叠前逆时偏移高阶有限差分算法及GPU实现[J].地球物理学报,2010,53(7):1725-1733 LIU H W,LI B,LIU H,et al.The algorithm of high order finite difference pre-stack reverse time migration and GPU implementation[J].Chinese Journal of Geophysics,2010,53(7):1725-1733

[20] 刘红伟,刘洪,邹振,等.地震叠前逆时偏移中的去噪与存储[J].地球物理学报,2010,53(9):2171-2180 LIU H W,LIU H,ZOU Z,et al.The problems of denoise and storage in seismic reverse time migration[J].Chinese Journal of Geophysics,2010,53(9):2171-2180

[21] 王保利,高静怀,陈文超,等.地震叠前逆时偏移的有效边界存储策略[J].地球物理学报,2012,55(7):2412-2421 WANG B L,GAO J H,CHEN W C,et al.Efficient boundary storage strategies for seismic reverse time migration[J].Chinese Journal of Geophysics,2012,55(7):2412-2421

[22] CLAPP R G.Reverse time migration with random boundaries[J].Expanded Abstracts of 79thAnnual Internat SEG Mtg,2009:2809-2813

[23] SHEN X K,CLAPP R G.Random boundary condition for memory-efficient waveform inversion gradient computation[J].Geophysics,2015,80(6):R351-R359

[24] CLAERBOUT J F.Toward a unified theory of reflector mapping[J].Geophysics,1971,36(3):467-481

(编辑：陈 杰)

A damped random boundary condition for prestack reverse time migration

KE Xuan1,SHI Ying1,2,ZHANG Yingying1,ZHANG Zhen3

(1.EarthScienceCollegeofNortheastPetroleumUniversity,Daqing163318,China;2.HeilongjiangProvincecollegescienceandtechnologyinnovationteam‘faultsdeformation,sealingabilityandfluidmigration’,Daqing163318,China;3.ResearchInstituteofExploration&Development,PetroChinaTarimOilfieldCompany,KorlaXinjiang841000,China)

The boundary conditions and storage requirements of reverse time migration (RTM) are often restricted to each other.The selection of these two parameters directly affect the imaging results and application conditions of RTM.Therefore,it is very important to study the boundary conditions and corresponding storage strategies for RTM.We proposed a damped random boundary condition,in which the energy attenuation layer and the random velocity layer were added outside of the real wavefield in turn.This method could effectively reduce the energy interference from random reflection.The inverse operation of the wave equation could reconstruct the source wavefield.Combined with cross-correlation imaging conditions,we conducted the RTM calculation.The results of comparison and analysis show that,compared with the random boundary condition,at the expense of less storage efficiency,the proposed method could obtain a better migration result,and the accuracy is very close to the results obtained by the perfectly matched layer boundary condition.The correctness of the above conclusion is verified by the example of salt model and big offset model.

reverse time migration (RTM),random boundary,storage,wavefield reconstruction

2016-09-27;改回日期：2017-04-15。

柯璇(1989—),男,博士在读,主要从事地震波场正演模拟与偏移成像等方面的研究。

石颖(1976—),女,教授,博士生导师,主要从事地震资料处理方面的研究。

国家自然科学基金项目(41574117,41474118)、黑龙江省杰出青年科学基金项目(JC2016006)、大连理工大学海岸和近海工程国家重点实验室开放基金项目(LP1509)、黑龙江省自然科学基金项目(D2015011)和东北石油大学研究生创新科研项目(YJSCX2016-002NEPU)联合资助。

P631

A

1000-1441(2017)04-0523-11

10.3969/j.issn.1000-1441.2017.04.008

This research is financially supported by the National Natural Science Foundation of China (Grant Nos.41574117,41474118),Heilongjiang Province Natural Science Fund for Distinguished Young Scholar (Grant No.JC2016006),the Open Project of State Key Laboratory of Coastal and Offshore Engineering of Dalian University of Technology (Grant No.LP1509),the Natural Science Foundation of Heilongjiang Province (Grant No.D2015011) and the Northeast Petroleum University Innovation Foundation for Postgraduate (Grant No.YJSCX2016-002NEPU).