物块在斜面体上运动的力学问题研究

陈玺君

(江苏省丹阳市吕叔湘中学；广西师范大学2016级在职教育硕士 江苏 镇江 212300)

物块在斜面体上运动的力学问题研究

陈玺君

(江苏省丹阳市吕叔湘中学；广西师范大学2016级在职教育硕士 江苏 镇江 212300)

研究了一个滑块在光滑的斜面体上运动的力学问题，给出了定量细致的推导过程，结论表明：物块的速度、位移随下落高度变量变化，加速度、作用力为定值，物体做匀变速直线运动，一对内力弹力分别做了功，但总功为零，且进行了教学方面的讨论．

滑块 力学问题 特征 方法

1 导言

高一年级机械能“功”这一节，教师往往都会举出这样一个典型的例题让学生思考：如图1所示，一质量为M，倾角为θ的光滑斜面体位于光滑的水平地面上处于静止状态，质量为m的物块(可视为质点)自斜面的顶端由静止开始沿斜面滑下．问：斜面体对物块的弹力是做正功、负功还是不做功？

其解答为：斜面体对物块的弹力对物块做负功．一般教师都是这样去跟学生讲解，先画出物块和斜面体初态和末态的位置，找出物块相对于斜面体的位移，进而让学生发现斜面体对物块的弹力与物块位移的方向夹角大于90°，因此弹力对物块做了负功．

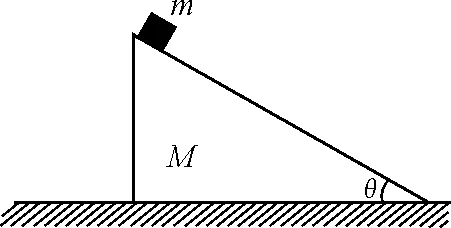
图1 原图

回答似乎很完美，然而，物块m和斜面体M分别相对于水平面做何种性质的运动？速度怎样？位移怎样？作用力怎样？功能关系又怎样？似乎故意避而不谈，有些物理学习程度好的学生去问时，老师甚至故意回避，以致学生不甚明确；再者，解决此问题的物理学方法论有什么特点？高中物理能够合理解决到什么程度？

本文从此出发，尽量用通俗的理论推导进行研究，力求获得相对详细的解答，以期为此问题的开放式教学提供详备的物理理论指导．

2 研究过程

为了这个问题，研究尽可能涉及更多的理论知识推导以获得相对详述的信息．取水平面为惯性参考系，研究对象：物块、斜面体．对物块、斜面体分别受力分析，如图2所示．

图2 受力分析图

沿水平方向为x轴、竖直向下为y轴，建立平面直角坐标系xOy，分别对物块m和斜面体M列牛顿第二定律方程有

Nsinθ=mamx

(1)

mg-Ncosθ=mamy

(2)

-N′sinθ=-MaMx

(3)

Mg+N′cosθ-F=0

(4)

由牛顿第三定律可知

N′=N

(5)

从以上式(1)～(5)来看，目前还无法判物块m和斜面体M相对于水平地面做什么性质的运动．

2.1 速度特征

设u为物块m相对于斜面体M的速度大小(方向沿斜面向下)，vm和vM分别为物块和斜面体相对于水平地面的速度大小，则有

(6)

其中x为物块沿斜面下滑的位移变量，h为物块下落的高度变量.

vmx=ucosθ-vMx

(7)

vmy=usinθ

(8)

由式(1) 、(3) 、(5)得

(9)

式(9)对时间0～t积分，得

(10)

(11)

式(11)也可由系统水平方向动量守恒可得．

由式(7)、(11)得

(12)

(13)

物块m和斜面体M组成的系统机械能守恒，有

(14)

由式(8) 、(12)、(13)、(14)得

(15)

将式(15)分别代入式(8)、(12)、(13)得

(16)

(17)

(18)

物块m相对水平地面的速度与水平方向的夹角α的正切值为

(19)

物块相对水平地面的速度大小为

(20)

由式(19) 、(20)可知物块m相对水平地面的速度的方向保持不变，大小随下落的高度h增大而增大．可见物块m相对水平地面的轨迹为直线，如图3所示．

图3

2.2 位移特征

由式(6)得

(21)

物块相对水平地面的元位移大小为

(22)

对式(22)进行0～h积分，再结合式(21)，有

(23)

得

(24)

同理可得

(25)

(26)

(27)

物块相对水平地面的位移与水平方向的夹角β的正切值为

(28)

这个结果和物块速度与水平方向的夹角完全相同．

物块相对水平地面的位移大小为

(29)

斜面体相对水平地面的元位移大小为

(30)

同理积分可得

(31)

斜面体M相对水平地面的位移大小为

(32)

物块和斜面体相对于水平地面水平方向的分位移之和为

(33)

2.3 加速度特征

式(15)、(16)、(17)、(18)分别对时间t求导，再结合式(21)，得

(34)

式(34)表示物块相对于斜面体的加速度．

(35)[3]

(36)

(37)

物块相对于水平面的加速度与水平方向的夹角γ的正切值为

(38)

这个结果和物块速度、位移与水平方向的夹角均相同．

物块相对于水平面的加速度大小为

(39)

式(19)、(38)表明，m的加速度方向和速度方向始终同向，且大小为定值．式(39)物块相对于水平地面的加速度大小保持不变．因此，综述物块相对于水平地面做匀加速直线运动．

式(37)表明，斜面体的加速度大小不变，方向水平向左，因此，斜面体相对于水平地面也做匀加速直线运动．

2.4 作用力特征

由式(1)、(4)、(5)、(35)得

(40)

F=Mg+N′cosθ=

(41)

式(40)、(41)表明，N和F均为定值，因而再次说明m和M分别相对于水平地面做匀变速直线运动．

2.4 功能关系特征

由式(22)、(25)、(30)及式(21) 、(5)、(40)推导可得

W=Nsinθdxm-Ncosθdym+N′sinθdxM=

(42)

由式(42)可知，一对相互作用力弹力(内力)N，N′的元功为零．

虽然一对相互作用力弹力(内力)N，N′的元功为零[1]，但过程中显然做了功，从分析并画出的运动轨迹可以看出(如图3所示)，斜面体对物块的弹力与物块位移的方向夹角大于90°，因此弹力N的确对物块做了负功．弹力N′对斜面体做了正功，一对内力N,N′在此分别对系统(m，M和地球)内各个物体做功，并没有消耗系统的机械能，在此做功起到了使系统内的机械能发生转化(物块的重力势能减少转化为物块水平方向的动能，物块竖直方向的动能以及斜面体水平方向的动能)，因此系统的机械能是守恒的．

3 综述

3.1 处理方法

上述研究采用的主要物理方法有隔离法、整体法、理想模型法、运动的合成与分解法、相对运动法、微分法、积分法．

3.2 教学指导意义

从大学普通物理学的角度来看，不能仅停留于此典型力学问题的一般解决，理应尽可能详实、深入的认识，另外还可以从物理学方法论方面加深研究．

当然，探索的结果表明物块、斜面体分别相对于水平地面做匀变速直线运动，轨迹如图所示．高中物理可以从物块、斜面体水平方向动量守恒[2]

mvmx=MvMx

再由几何关系[2]

是可以求出物块、斜面体分别相对于水平地面的位移大小的，然而物块水平方向和竖直方向的分速度、物块相对地面的合速度、斜面体的速度以及物块、斜面体运动的加速度和受到的弹力是无法求解的，虽然不是变力，却涉及到微积分，高中物理目前不涉及到微积分知识，所以无能为力．高中物理能够合理解决的有式(1)～(9)、(11)～(20)，运动的方法有理想模型法、运动的合成与分解、相对运动法、隔离法与整体法．

4 结束语

本文详实、细致地研究了一个高中典型力学问题，首先获得了关于这个问题的速度、位移、加速度、作用力、功能关系，加深了对此问题的定量认识，使之不再停留在感性的认知上．其次总结了解决此问题的物理学方法，从大学普通物理和高中物理两个不同的角度来审视此问题的可行性特点，为此问题的开放式教学提供详备的物理理论指导．再次，此问题可以成为一个很好的高中物理与大学普通物理衔接的实例．

1 梁绍荣，刘昌年，盛正华.普通物理学·力学(第二版).北京：高等教育出版社，1987

2 漆安慎.普通物理学教程·力学(第二版)学习指导书.北京：高等教育出版社，2009

3 江苏省物理学会主编.物理学奥赛教程(增订本).南京：南京大学出版社，2004.06

2017-03-10)