复合函数求单调区间的数形结合方法

冯艳超

【中图分类号】G633.6 【文獻标识码】A 【文章编号】2095-3089（2017）28-0133-01

对于复合函数求单调区间的问题常用解决方法有两种：第一种方法可以用导数方法来求；但是解不等式有的时候难度很大；第二种方法可以用数形结合的方法来求。这种求复合函数单调区间的方法直观、简便、易懂、便于学生掌握，是值得一试的好方法。现将这种方法解析如下：

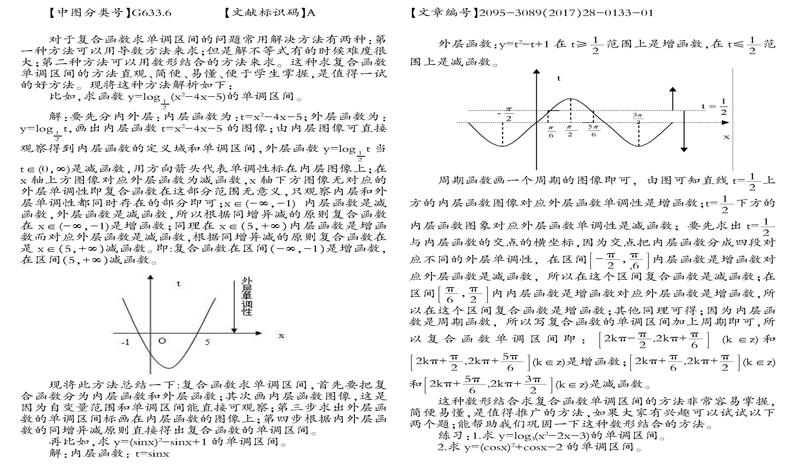
比如，求函数y=log■（x2-4x-5）的单调区间。

解：要先分内外层：内层函数为：t=x2-4x-5；外层函数为： y=log■t，画出内层函数t=x2-4x-5的图像；由内层图像可直接观察得到内层函数的定义域和单调区间，外层函数y=log■t当t∈（0，∞）是减函数，用方向箭头代表单调性标在内层图像上；在x轴上方图像对应外层函数为减函数，x轴下方图像无对应的外层单调性即复合函数在这部分范围无意义，只观察内层和外层单调性都同时存在的部分即可；x∈（-∞，-1）内层函数是减函数，外层函数是减函数，所以根据同增异减的原则复合函数在x∈（-∞，-1）是增函数；同理在x∈（5，+∞）内层函数是增函数而对应外层函数是减函数，根据同增异减的原则复合函数在是x∈（5，+∞）减函数。即：复合函数在区间（-∞，-1）是增函数，在区间（5，+∞）减函数。

现将此方法总结一下：复合函数求单调区间，首先要把复合函数分为内层函数和外层函数；其次画内层函数图像，这是因为自变量范围和单调区间能直接可观察；第三步求出外层函数的单调区间标画在内层函数的图像上；第四步根据内外层函数的同增异减原则直接得出复合函数的单调区间。

再比如，求y=（sinx）2-sinx+1的单调区间。

解：内层函数： t=sinx

外层函数：y=t2-t+1在t≥■范围上是增函数，在t≤■范围上是减函数。

周期函数画一个周期的图像即可，由图可知直线t=■上方的内层函数图像对应外层函数单调性是增函数；t=■下方的内层函数图象对应外层函数单调性是减函数；要先求出t=■与内层函数的交点的横坐标，因为交点把内层函数分成四段对应不同的外层单调性，在区间-■，■内层函数是增函数对应外层函数是减函数，所以在这个区间复合函数是减函数；在区间■，■内内层函数是增函数对应外层函数是增函数，所以在这个区间复合函数是增函数；其他同理可得；因为内层函数是周期函数，所以写复合函数的单调区间加上周期即可，所以复合函数单调区间即：2k？仔-■，2k？仔+■（k∈z）和2k？仔+■，2k？仔+■（k∈z）是增函数；2k？仔+■，2k？仔+■（k∈z）和2k？仔+■，2k？仔+■（k∈z）是减函数。

这种数形结合求复合函数单调区间的方法非常容易掌握，简便易懂，是值得推广的方法，如果大家有兴趣可以试试以下两个题；能帮助我们巩固一下这种数形结合的方法。

练习：1.求y=log3（x2-2x-3）的单调区间。

2.求y=（cosx）2+cosx-2的单调区间。