横观各向同性岩体中复杂地应力反演参数敏感度分析

张志增,张 欣

(中原工学院建筑工程学院,河南郑州450007)

横观各向同性岩体中复杂地应力反演参数敏感度分析

张志增,张 欣

(中原工学院建筑工程学院,河南郑州450007)

为了分析复杂地应力情况下横观各向同性岩体参数对地应力反演结果的影响程度,假定岩体参数在±50%的波动范围内变化并进行数值模拟,观察反演结果的变化情况。结果表明,已知参数波动越大,反演结果失真程度越高,呈现线性相关性。各向同性面内的弹性模量E的精确度对反演结果影响最大,垂直各向同性面方向的泊松比μ′次之,各向同性面内的泊松比μ再次之,垂直各向同性面方向的弹性模量E′对反演结果影响较小。

横观各向同性岩体；地应力；反演参数；敏感度

0 引 言

进入21世纪以来,伴随着岩土工程建设项目规模的不断加大,其复杂程度与难度也随之提升[1],岩土体地应力参数的精准获得成为岩土工程的一项重要研究课题[2]。岩土体地应力参数选取的精确与否决定着工程设计与施工的成败。现场原位试验法、试验室试验和经验类比法等确定岩土体地应力的方法存在局限,不能反映真实的岩土体地应力状况[3-5]。大量研究表明,基于现场量测信息的位移反分析方法为岩土体地应力参数的确定开辟了一条新道路,在岩土工程中发挥了重要的作用[6-7]。

上世纪70年代初期,Kavanagh和Clough为位移反分析方法奠定了一定的理论基础[8]。经过40多年的发展,位移反分析方法的研究在国内外已经取得了丰硕的成果,研究涉及弹性问题、粘弹性问题、弹塑性问题和横观各向同性问题[9-12]。岩体的初始地应力作为岩土工程的重要参数,一直是国内学者研究的重要对象[13-15]。纵观已有地应力反演的文献,大多针对优化方法展开研究,关于地应力反演的稳定性研究鲜有报道。张志增[16]推导了横观各向同性岩体中巷道位移的解析解,并进行了位移反分析的唯一性分析。本文在上述研究的基础上,对横观各向同性岩体中复杂地应力反演的参数敏感度进行分析。

1 计算模型的基本假定

建立如图1所示的坐标系。假定xoy面为横观各向同性面,oz为对称轴。横观各向同性岩体中深埋圆形巷道模型见图2。图中,p为竖直方向地应力；q为水平地应力；τ为剪应力。基本假设如下：①巷道围岩为横观各向同性弹性体,开挖后位移和应变均为微小；②巷道走向垂直于横观各向同性面；③模型为平面应变问题；④巷道为埋深巷道,忽略巷道上、下部的初始应力差；⑤忽略影响范围内的自重[17]。

图1 横观各向同性材料示意

图2 深埋圆形巷道模型

2 参数敏感度分析

2.1 数值模型

根据位移反分析唯一性理论,张志增[18]推导得到了地应力p、q和τ的反分析表达式并指出,如果同时反分析p、q和τ,至少需要已知3个测点的位移值和其他各个岩体参数。

采用数值计算软件FLAC3D,建立1个横观各向同性岩体中圆形巷道模型。巷道半径a=2 m、各向同性面内的弹性模量E=1 GPa、垂直各向同性面方向的弹性模量E′=0.8 GPa、各向同性面内的泊松比μ=0.25、垂直各向同性面方向的泊松比μ′=0.3、p=10 MPa、q=20 MPa、τ=3 MPa。由FLAC3D计算得到该模型的位移云图见图3,可以读出模型中任意点的位移值。

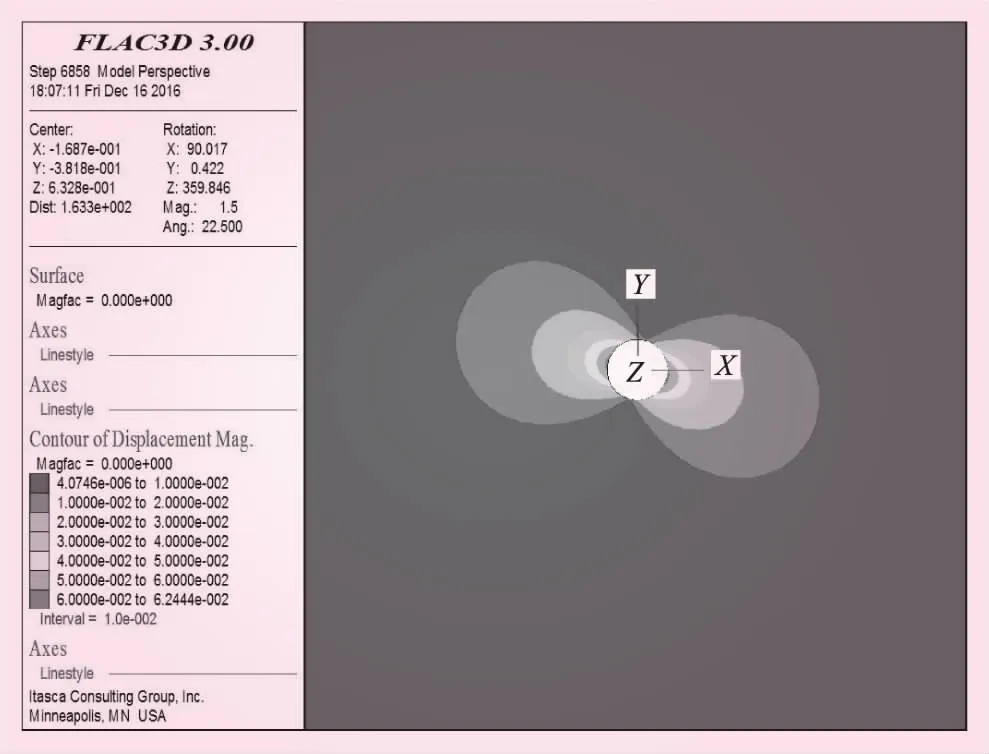
图3 圆形巷道模型的位移云图

选取点1(2,60°)、点2(2,90°)和点3(2,120°)的位移值u1=0.014 816 m、u2=0.014 59 m、u3=0.037 614 m用于反分析计算,求得p=10.08 MPa、q=20.19 MPa、τ=2.86 MPa。与精确值相比,相对误差分别为0.82%、0.95%、4.62%,这证明了反分析的精确度。下面通过调整不同参数的取值,分析各参数对反分析结果的敏感度。

2.2 各向同性面内的弹性模量E

对各向同性面内弹性模量E进行波动,赋予不同的值以计算反分析结果。将E波动时与精确时的反演值对比,进行误差分析,结果见表1；再将E波动时的反演值与标准地应力值对比,进行误差分析,结果见表2。E波动时与精确时的反演值之间的相对误差见图4；与标准地应力值之间的相对误差见图5。

由表1、2和图4、5可以看出,弹性模量E的波动对反分析结果的影响呈现出一定的线性相关性,参数的误差越大,反分析值误差越大。从指导工程角度来看,弹性模量E误差在10%内,反分析结果的相对误差较小,此时反分析的结果仍具有可信度。

2.3 各向同性面内的泊松比 μ

对各向同性面内泊松比μ进行波动,赋予不同的值以计算反分析结果。将μ波动时与精确时的反演值对比,进行误差分析,结果见表3；再将μ波动时的反演值与标准地应力值对比,进行误差分析,结果见表4。μ波动时与μ精确时的反演值之间的相对误差

表1 E波动时与精确时反演值对比

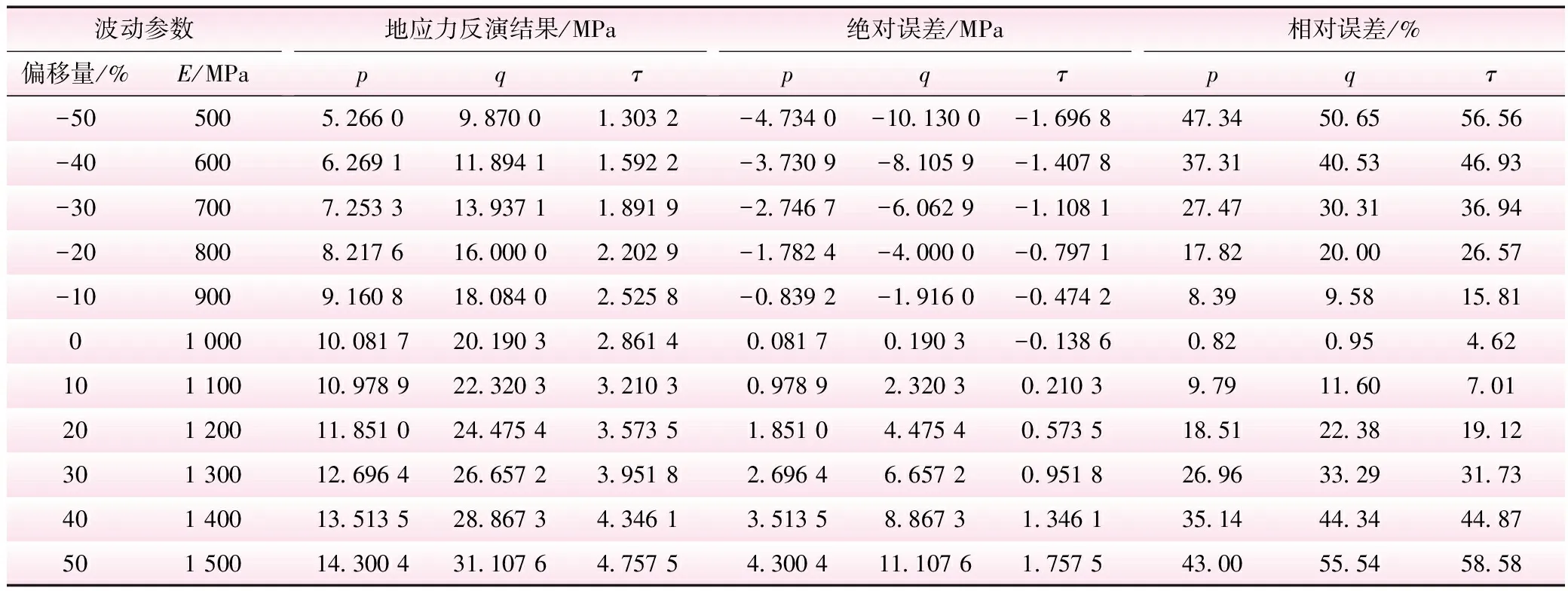
表2 E波动时反演值与标准地应力值对比

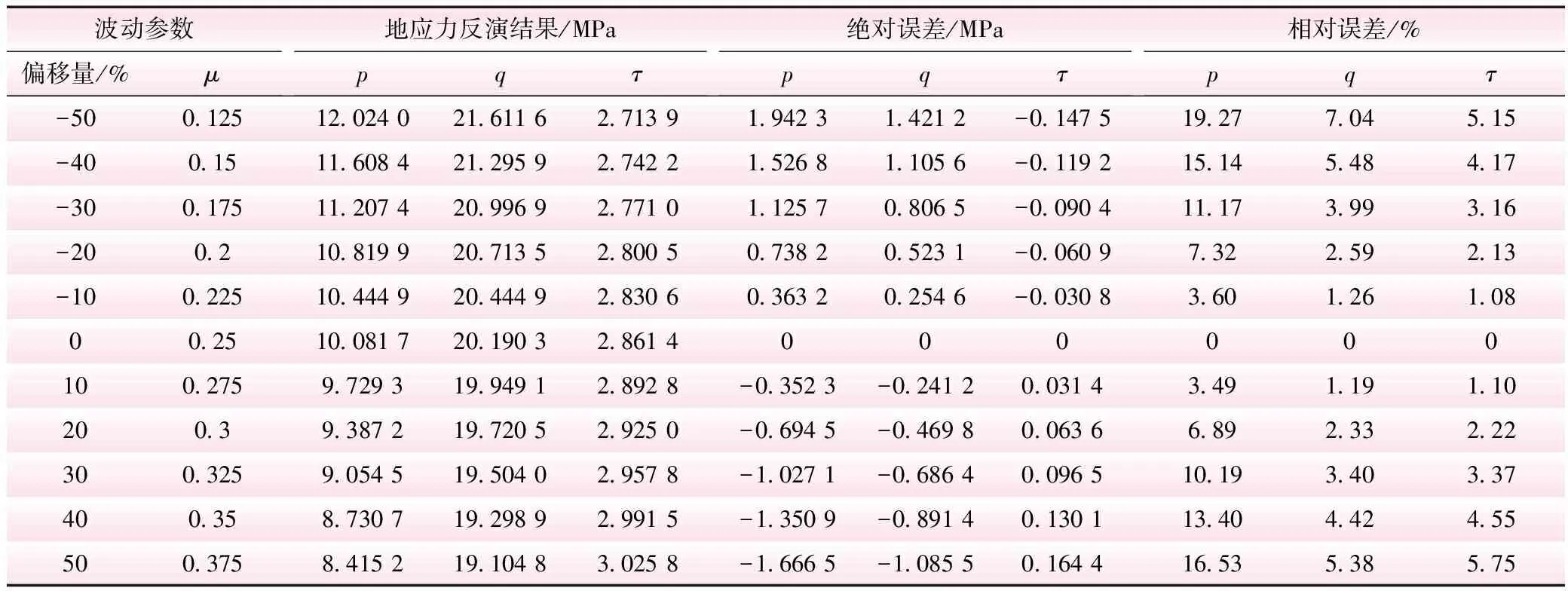
表3 μ波动时与精确时反演值对比分析

见图6。与标准地应力值之间的相对误差见图7。

由表3、4和图6、7可以看出,泊松比μ的波动对反分析结果的影响呈现出一定的线性相关性,参数的误差越大,反分析值误差越大。从指导工程角度来看,泊松比μ误差在30%内,反分析结果的相对误差较小,此时反分析的结果仍具有很大的可信度。

表4 μ波动时反演值与标准地应力值对比分析

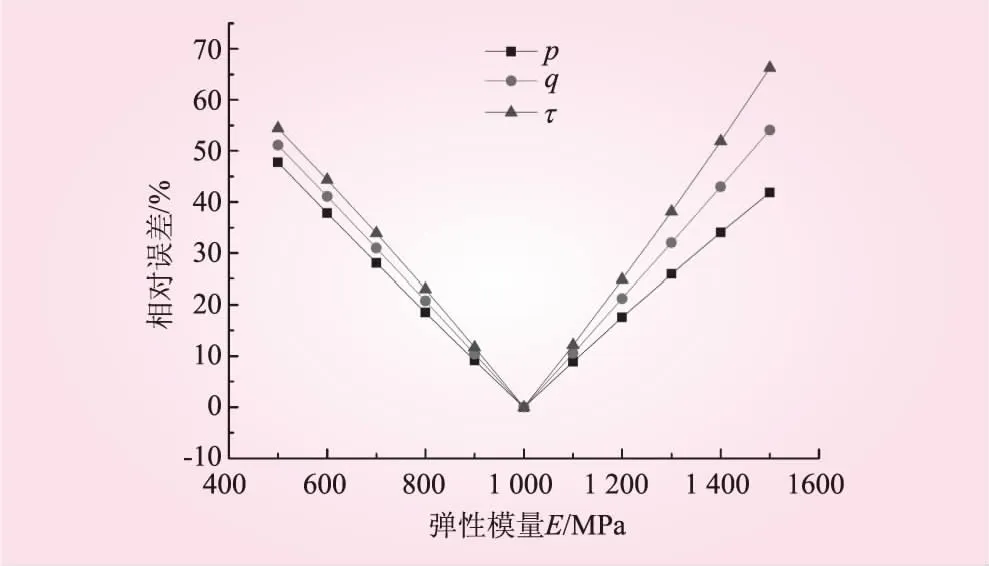
图4 E波动时与精确时反演值的相对误差

图5 E波动时反演值与标准地应力值的相对误差

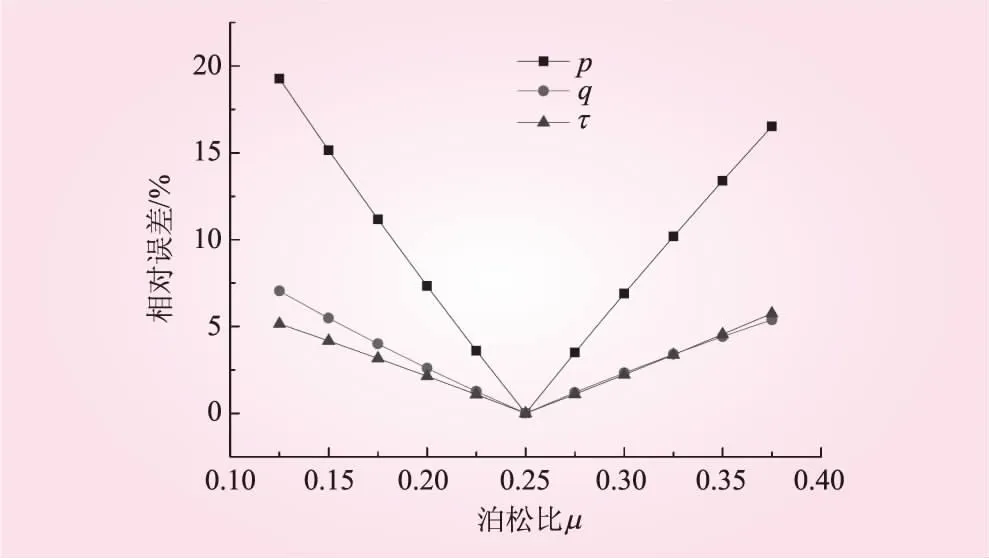
图6 μ波动时与精确时反演值的相对误差

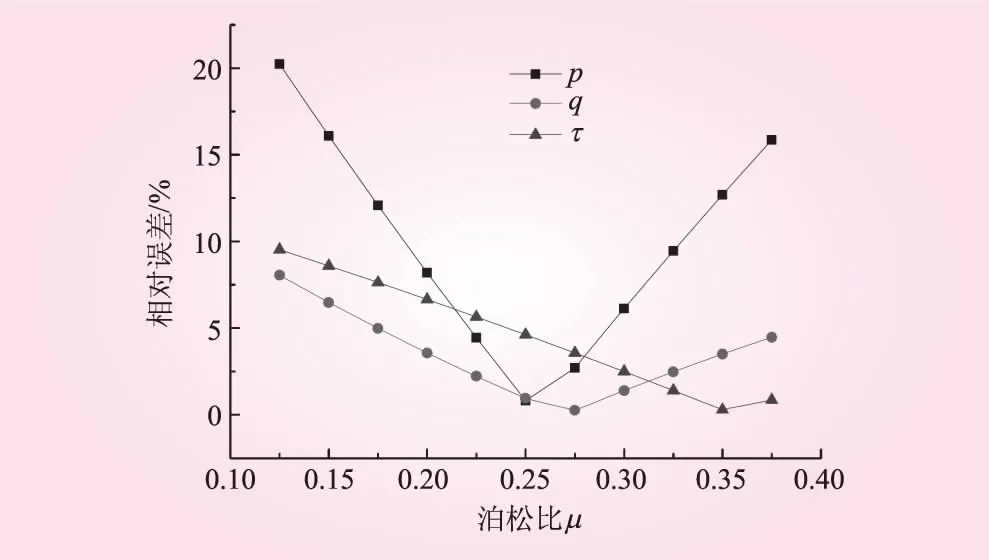
图7 μ波动时反演值与标准地应力值的相对误差

2.4 垂直各向同性面方向的弹性模量E′

对垂直各向同性面方向的弹性模量E′进行波动,赋予不同的值以计算反分析结果。将E′波动时与精确时的反演值对比,进行误差分析,结果见表5；再将E′波动时的反演值与标准地应力值对比,进行误差分析,结果见表6。E′波动时与精确时的反演值之间的相对误差见图8；与标准地应力值之间的相对误差见图9。

由表5、6和图8、9可以看出,弹性模量E′的波动对反分析结果的影响呈现出一定的线性相关性,参数误差越大,反分析值误差越大。从指导工程角度来看,弹性模量E′误差在40%内,反分析结果的相对误差较小,此时反分析的结果仍具有很大的可信度。

2.5 垂直各向同性面方向的泊松比 μ′

对垂直各向同性面方向的泊松比μ′进行波动,赋予不同的值计算反分析结果。将μ′波动时与精确时的反演值对比,进行误差分析,结果见表7；再将μ′波动时的反演值与标准地应力值对比,进行误差分析,结果见表8。μ′波动时与精确时的反演值之间的相对误差见图10；与标准地应力值之间的相对误差见图11。

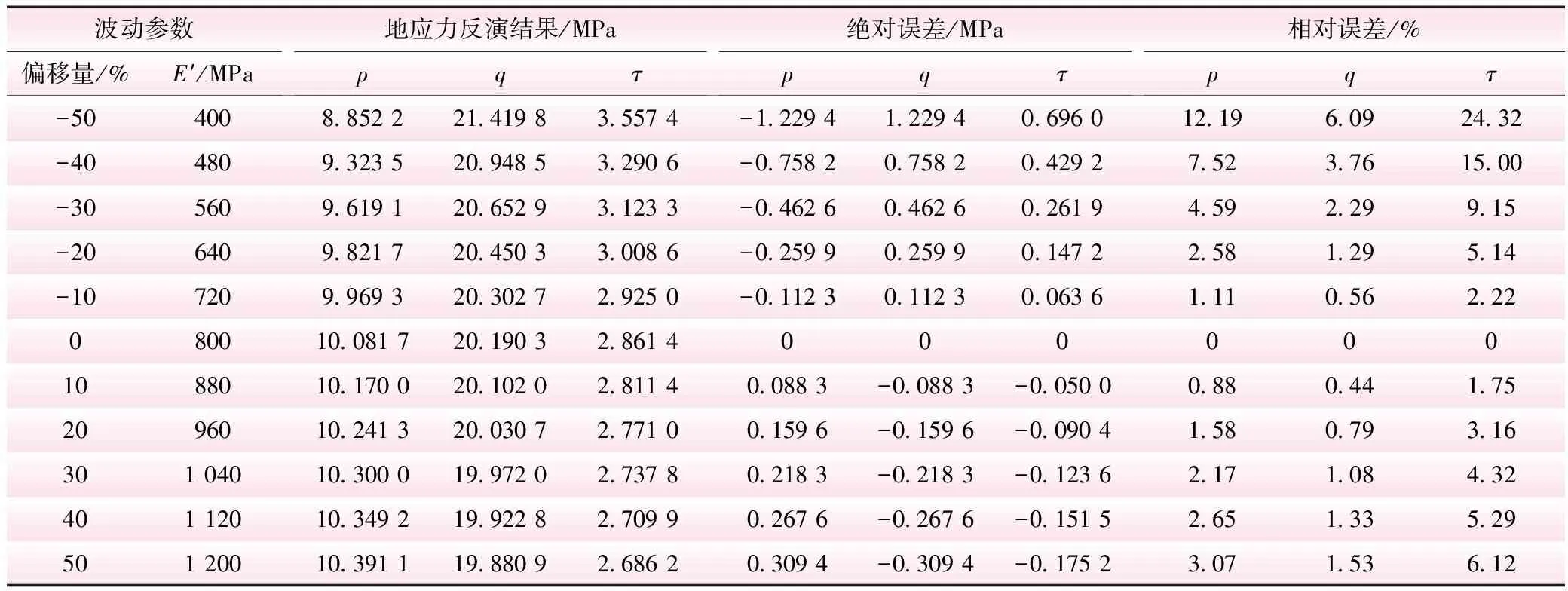
表5 E′波动时与精确时反演值对比分析

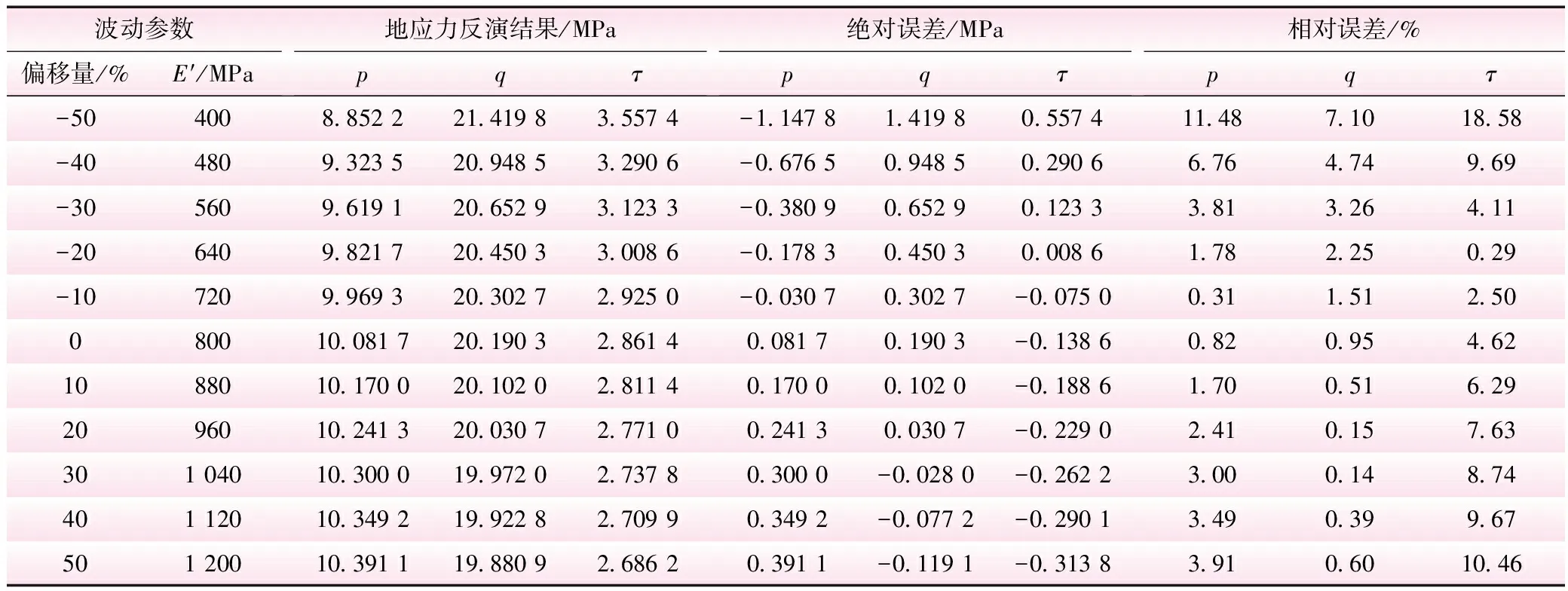
表6 E′波动时反演值与标准地应力值对比分析

表7 μ′波动时与精确时反演值对比分析

由表7、8和图10、11可以看出,泊松比μ′的波动对反分析结果的影响呈现出一定的线性相关性,参数的误差越大,反分析值误差越大,但在一定程度上对反分析值的影响是较小的。从指导工程角度来看,泊松比μ′误差在20%内,反分析结果的相对误差较小,此时反分析的结果仍具有可信度。

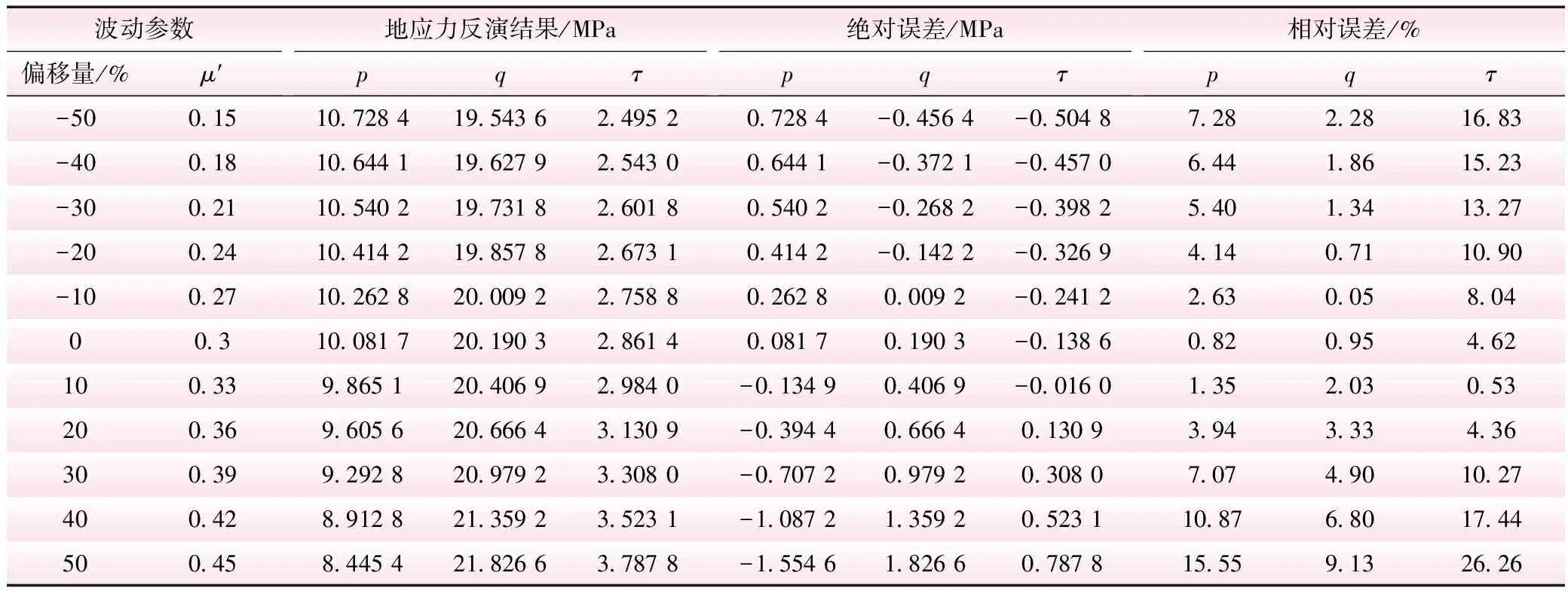
表8 μ′波动时反演值与标准地应力值对比分析

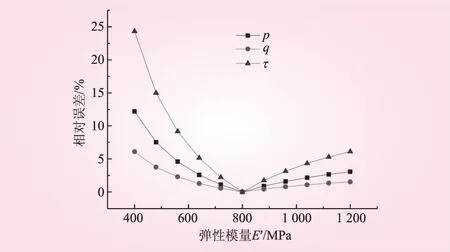
图8 E′波动时与精确时反演值的相对误差

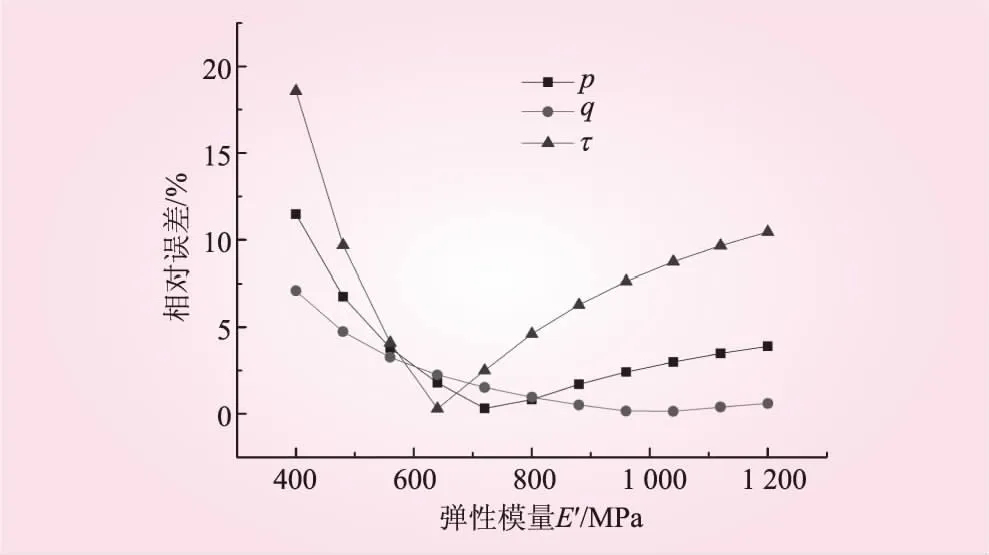
图9 E′波动时反演值与标准地应力值的相对误差

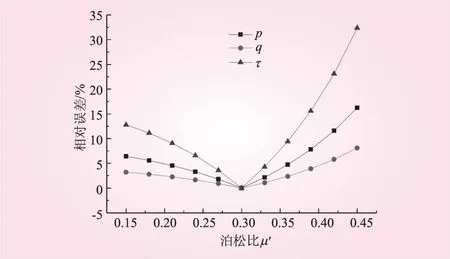
图10 μ′波动时与精确时的相对误差

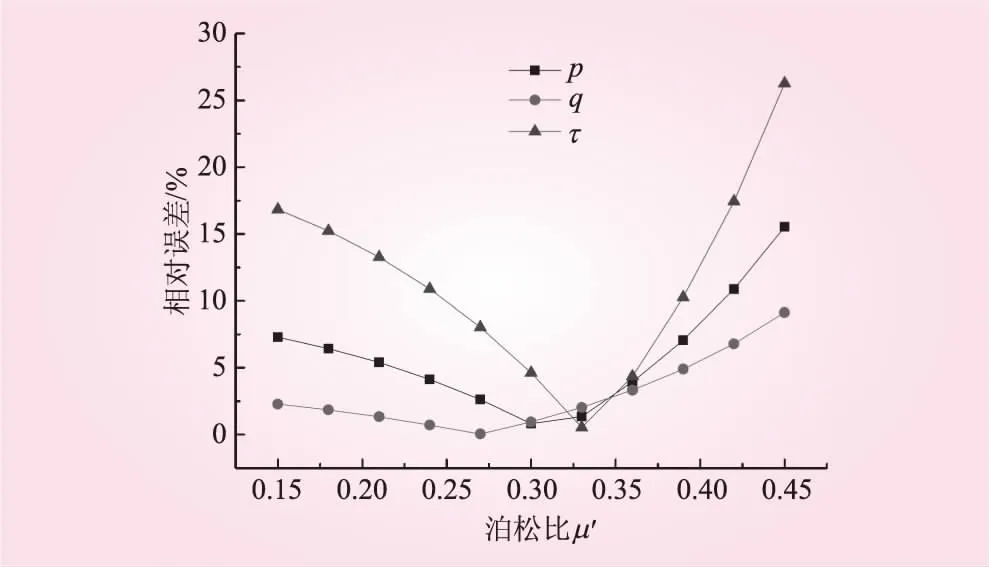
图11 μ′波动时反演值与标准地应力值的相对误差

3 结 语

通过对横观各向同性岩体深埋圆形巷道反分析模型中地应力反演时的参数敏感度进行分析,可以得出以下结论：

(1)在反分析具有唯一性的前提下,横观各向同性岩体深埋圆形巷道反分析模型能够通过位移解析解进行地应力反分析计算,其结果是可靠的。

(2)应用深埋圆形巷道反分析模型进行地应力反演计算时,各已知参数的精度对反演值结果的影响呈现线性相关性,参数的误差越大,反演值精度越低。

(3)横观各向同性岩体中深埋圆形巷道反分析模型中的参数敏感程度如下：弹性模量E的精确度对反演值结果影响最大,泊松比μ′次之,泊松比μ再次之,弹性模量E′影响最小,其误差分别在10%、20%、30%、40%以内时反分析的结果仍具有可信度。

(4)在使用横观各向同性岩体深埋圆形巷道反分析模型进行地应力反演计算时,应重点把握提高各个参数的精度,以确保反分析结果的精度。

[1]王思敬. 中国岩石力学与工程世纪成就[M]. 南京： 河海大学出版社, 2004．

[2]高大钊, 孙钧. 岩土工程的回顾与前瞻[M]. 北京： 人民交通出版社, 2001．

[3]周维垣, 杨强. 岩石力学数值计算方法[M]. 北京： 中国电力出版社, 2005．

[4]李晓红, 靳晓光, 亢会明, 等. 隧道位移智能化反分析及其应用[J]. 地下空间与工程学报, 2001, 21(4)： 299- 304．

[5]刘汉东. 岩体力学参数优选理论及应用[M]. 郑州： 黄河水利出版社, 2006．

[6]王芝银, 杨志法, 王思敬. 岩石力学位移反演分析回顾及进展[J]. 力学进展, 1998, 28(4)： 488- 498．

[7]赵新铭, 刘宁, 张剑. 岩土力学反分析的数值反演方法[J]. 水利水电科技进展, 2003, 23(2)： 55- 58.

[8]KAVANAGH K T, CLOUGH R W. Finite element applications in the characterization of elastic solids[J]. International Journal of Solids & Structures, 1971, 7(1)： 11- 23．

[9]杨志法, 刘竹华. 位移反分析法在地下工程设计中的初步应用[J]. 地下工程, 1981(2)： 9- 14.

[10]杨志法, 熊顺成, 王存玉, 等. 关于位移反分析的某些考虑[J]. 岩石力学与工程学报, 1995, 14(1)： 11- 16．

[11]陈子萌. 由位移测定值反算流变岩体变形性质参数及地应力[J]. 煤炭学报, 1982(4)： 45- 51．

[12]张志增. 横观各向同性岩体位移反分析的理论与应用研究[D]. 北京： 清华大学, 2010．

[13]马行东. 不同地应力下的地下硐室动态特征分析[J]. 矿业研究与开发, 2007(2)： 20- 22, 91．

[14]饶运章, 饶睿, 王柳, 等. 三维初始应力场在FLAC～(3D)中的反演与重构实现[J]. 矿业研究与开发, 2014(1)： 11- 15．

[15]梁波. 隧道工程[M]. 重庆： 重庆大学出版社, 2015．

[16]张志增, 李小昌, 王克忠. 考虑剪应力作用时横观各向同性岩体中圆形巷道位移反分析的惟一性[J]. 岩土力学, 2016(S2)： 449- 460．

[17]谷兆祺, 彭守拙, 李仲奎. 地下洞室工程[M]. 北京： 清华大学出版社, 1994．

[18]张志增. 横观各向同性岩体中位移反分析的基础理论研究[M]. 武汉： 华中科技大学出版社, 2017．

(责任编辑杨 健)

ParameterSensitivityAnalysisonMultiplexGroundStressBackAnalysisinTransverseIsotropicRockMass

ZHANG Zhizeng, ZHANG Xin
(School of Civil Engineering and Architecture, Zhongyuan University of Technology, Zhengzhou 450007, Henan, China)

In order to analyze the effect degree of parameters of transverse isotropic rock mass on geo stress back analysis, the numerical simulation when the rock mass parameters are fluctuated in a range from -50% to +50% is carried out to observe the changes of results of geo stress back analysis parameter. The results show that if the fluctuation of parameter relative to exact value is greater, the distortion degree of back analysis result will be higher. The fluctuation of known parameter has a linear correlation with the results of back analysis. The accuracy of modulus of elasticityEhas greatest impact on back analysis results, the impact of Poisson’s ratioμ′ is weaker than the former, the impact of Poisson’s ratioμis in the third place, and the impact of modulus of elasticityE′ is relatively minor．

transverse isotropic rock mass; geo stress; back analysis parameter; sensitivity

2017- 01- 03

NSFC-河南人才培养联合基金项目(U1204509)；河南省高等学校青年骨干教师资助计划项目(2015GGJS-192)；河南省高等学校重点科研项目资助计划项目(15A570005)

张志增(1980—),男,河南郑州人,副教授,博士,主要从事岩土与地下工程的教学和研究工作．

TD311

：A

：0559- 9342(2017)06- 0032- 07