混凝土压缩薄膜效应的发展历史及研究现状
葛 楠
(长安大学公路学院,陕西 西安 710061)
混凝土压缩薄膜效应的发展历史及研究现状
葛 楠
(长安大学公路学院,陕西 西安 710061)
本文对混凝土压缩薄膜效应工作原理进行了详细解读,阐述分析了相关计算理论的发展,对比各个理论的特点,找出了最适用理论依据,并将压缩薄膜效应与当代建筑桥梁相结合,提出未来研究方向,在保障结构安全的前提下实现最大经济效益。
压缩薄膜效应;拱效应;混凝土梁板;抗弯承载力
1 概述
钢筋混凝土结构作为当今重要的建筑桥梁结构之一,其结构性能一直是相关学科研究主题之一。试验表明,对于有侧向约束的钢筋混凝土梁板,压缩薄膜的存在使其实际承载力远大于解析结果。
混凝土压缩薄膜效应,又称内拱效应。如图1所示,受到侧向约束的混凝土梁板在荷载作用下,受拉区混凝土开裂,产生变形之后,约束端将会产生侧向阻力。在此侧向阻力的影响下,裂缝的发展得以抑制,中性轴上移速度减慢,受压区面积增大,从而构件承载能力提升。这种现象在单向板中被称为混凝土板的內拱效应,而对于双向板,则称之为混凝土压缩薄膜效应。
由于混凝土压缩薄膜效应的存在,构件承载能力远大于预估值,若能充分利用混凝土压缩薄膜效应,则可在设计时减少钢筋用量,在保障结构安全的前提下,取得更大的经济效益。

图1 拱效应理想模型
2 国外早期研究
2.1 压缩薄膜效应的提出
1921年,Westergaard,H.M.和 Slater,W.A.在对美国工程协会在圣路易斯做的一系列研究试验进行分析时发现,对于开裂构件,根据测得应力反算的构件抗弯承载力明显小于实际承载力,最大挠度的计算结果与实际测量的平均最大挠度值相差较大[1]。他们认为,承载能力的差异可能来源于钢筋与混凝土之间的粘结,裂缝处的混凝土和钢筋的相互作用对承载能力的影响大于预想结果。虽然这种猜测被后续研究证明可能性较小,但承载能力试验与理论结果差异性的提出,使之成为混凝土压缩薄膜效应研究的良好开端。由于条件的限制,试验仅考虑了钢筋混凝土单向板,所得结果具有一定的局限性。
直至1952年,在对南非一家医院进行拆除时,Ockleston才得以对完整的钢筋混凝土结构进行加载试验[2]。试验发现,在构件加载初期,裂缝尚未出现,试验挠度与计算结果吻合较好。随着荷载的增加,裂缝出现并向中性轴发展。此时的实际挠度相对于理论结果偏小。这种现象在双向板中同样出现。将试验结果与按1934钢筋混凝土规范及按塑性铰线法计算的结果对比后发现,1934规范大幅低估了构件的承载力,仅为实际承载力的1/4;而屈服线理论仅适用于单向板,对于双向板,这种方法的计算准确性大幅降低。至此,传统承载能力计算方法的局限性才广为关注。
1956年,Mcdowell E.L.等人在对砌体墙进行荷载试验时发现,受侧向约束的墙体开裂后的变形与三铰拱相似,从而第一次正式提出了拱效应的概念[3]。研究表明,拱推力的大小与接触面应变直接相关。基于变形协调关系,应变分布满足:

式中,R和u为无量纲量,R反映了构件的弹性变形,u反映了板带位移。ec为砌体墙的塑性应变,d1为1/2梁高,Lr为1/2跨径,w为梁跨中挠度。
在Mcdowell的模型中,拱推力及相应的承载能力的提高主要由R和u决定,计算公式见表1:

表1 拱效应内力分析 (Mcdowell et al.,1956)
表中sc为砌体墙最大压应力,Mu则为拱效应弯矩。
近年来,越来越多的产品外观设计以传统图案为设计元素。传统图案的应用不仅给人们带来了无限的创作灵感,还给产品增添了丰富的文化底蕴,从而使产品价值得以有效提升。
Mcdowell的理论建立在理想弹塑性关系的基础之上,试验对象为砌体结构。考虑到砌体结构与素混凝土结构的受力性能相似,该理论亦可运用于素混凝土结构之中,并为之后对钢筋混凝土梁板拱效应的研究奠定了理论基础。
2.2 基于压缩薄膜效应的计算理论
1964年,Robert Park提出了基于塑性理论的膜效应理论[4],对两端固接的框架梁的破坏机制进行了假定 (见图2),认为破坏时形成对称的四个塑性铰。根据轴向力和弯矩的平衡条件,可得拱推力N及抵抗弯矩M为:


图2 两端固接框架梁破坏形态
式中,Cc为混凝土产生的压力,Cs为压区钢筋产生的压力,T为拉区钢筋拉力,u为6英寸见方的混凝土抗压强度,k1k3表示截面混凝土平均应力与抗压强度的比值,k2反应了截面混凝土的压应力分布情况。k1k3及k2的取值服从Hognestad模型[5](见图 3)。
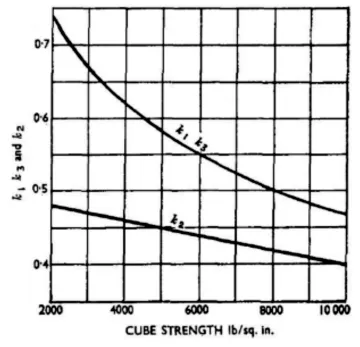
图3 压应力系数与抗压强度关系曲线(Hognestad et al.,1955—1956)
根据虚功原理,综合分析计算模型的几何关系及静力平衡条件,可得如下方程:

在上述方程中,d为梁高,d1为混凝土受压区最外层纤维到拉区钢筋合力作用点的距离,d2为混凝土受压区最外层纤维到压区钢筋合力作用点的距离。
Park发现,在此方程中,右侧第二项与Johansen提出的塑性铰线法得到的结果接近,故而推断,方程 (5)中的右侧第一项即反映了混凝土梁板的压缩薄膜效应。这一计算方法的准确性,在后来的研究中也得以验证[6][7]。
早期压缩薄膜效应的研究对象主要为砌体结构、素混凝土结构或低配筋混凝土结构。1984年,Kirkpatrick,Rankin,及 Long在Mcdowell的研究基础上,提高混凝土板配筋率,并通过调整板的跨径设立对比试验[8]。试验结果分析发现,在局部荷载作用下,冲切破坏为该类结构最常见的破坏形式,而弯曲破坏的发生机率相对较小。根据其分析结果,混凝土板的最大拱弯矩可以表示为:

在此公式中,k为拱弯矩影响系数。对于刚塑性材料,k取0.21。Kirkpatrick等人认为拱效应仅出现在结构屈服之后的破坏阶段,在理论推导过程中将混凝土视为塑性材料。实际上,拱效应在开始变形后已经逐步产生,需考虑混凝土弹—塑性材料性能的影响,k的取值应与应力大小相匹配。
之后,1997年,Rankin和Long对先前研究进行了进一步完善,对Mcdowell理论中的R和u值进行了分析简化,并将混凝土板简化为带有两端固接、带有弹性横向支撑的三铰拱[9]。所得的拱长转化公式记为


对于均布荷载,k值取8/L;对于跨中集中荷载,k值取4/L。
Rankin将变形理论与混凝土弹塑性本构关系相结合,并且首次尝试采用等效约束的方法确定侧向刚度对混凝土压缩薄膜的影响,对后续研究有着十分重要的意义。
3 国内外研究现状
2001年,英国的Taylor将Rankin的理论算法进一步拓展,发现在高强混凝土板中压缩薄膜效应更为明显[10],她指出,压缩薄膜效应作用下的拱弯矩可以表示为

式中A为混凝土在成拱区内有效面积。
在Rankin此次理论中,混凝土板的抵抗弯矩由在压缩薄膜效应下的拱弯矩和抗弯弯矩共同组成,抵抗弯矩及承载力可用下式计算。
板的冲切承载力的计算依旧采用Kirkpatrick的研究理论。
之后,郑愚[11]、王刚[12]等人在此基础上做了一系列桥梁缩尺模型的加载试验,经试验结果与各种理论计算结果的对比分析,发现Taylor的理论计算结果与实际承载力吻合度最高,拥有较好的适用性,故之后的研究主要基于这一计算理论。
郑愚的研究最为突出,她在之前理论的基础上,将压缩薄膜效应与现代混凝土梁进行了结合,采用非线性有限元方法对有横向约束的混凝土板进行数值模拟,准确模拟了侧向约束作用下的混凝土板的工作性能,并获得试验过程中较难采集的结构属性[13],证明了压缩薄膜效应的存在及产生过程。 此外,她还对交通荷载作用下的 FRP 筋、 GFRP 筋桥梁进行研究[14][15], 分析了新型高强度加筋混凝土桥梁的工作性能、破坏机理和承载能力。她的研究表明,对压缩薄膜效应的应用可降低配筋率,提高结构的耐久性,降低建造维修成本,解决了频繁更换钢筋对交通的干扰。
4 结语
混凝土压缩薄膜效应自发现至今已有近百年,随着科学的发展,计算理论不断完善。目前,对混凝土压缩薄膜效应的研究已从先前的理论研究转向应用研究。当前的研究趋势包括其在不同现代化建筑桥梁中的产生、影响压缩薄膜效应的因素分析、高效利用压缩薄膜效应改变结构外形并带来经济效益等。有限元数值模拟的发展解决了较难试验的测量问题,也解决了缩尺试验带来的性能偏差。
[1]Westergaard HM and WA Slater.Moments and stresses in slabs[C].Proceedings of the AmericanConcrete Institute(17) .Washington,D.C.:National research council,1921:415-538.
[2]Ockleston AJ.Load tests on a three storey building in Johannesburg [J].The Structural Engineer,1955,33 (10): 304-322.
[3]Mcdowell EL,KE.Mckee and E Sevin.Arching action theory of masonry walls[J].Journal of the Structural Division,1956,82 (ST2): 915/1-915/18.
[4]Park R.Ultimate strength of rectangular concrete slabs under short-term uniformloading with edges restrained against lateral movement [J].ICE Proceedings,1964,28 (2) :125-150.
[5]Hognestad E,NW Hanson and D Mchenry.Concrete stress distribution in ultimate strengthdesign [J].Journal of the American Concrete Institute,1955,52 (6) :455-479.
[6]Powell DS.Ultimate strength of concrete panels subjected to uniformly distributed loads[D].Cambridge:Cambridge U-niversity Thesis,1956.
[7]Wood RH.Plastic and elastic design of slabs and plates [M].London:Thames and Hudson,1961:353-362.
[8]Kirkpatrick J,GIB Rankin and AE Long.Strength evaluation of M-beam bridge deck slabs [J].Engineering Structures,1984,62B (3): 60-68.
[9]Rankin GIB and AE Long.Arching action strength enhancement in laterallyrestrainedslab strips [J].Structures&Buildings,1997,122 (4): 461-467.
[10]Taylor SE,GIB Rankin and DJ Cleland.Guide to compressive membrane action in concretebridge decks[M].Camberley,Surrey:Concrete Bridge Development Group,2002.
[11]Zheng Yu,Su Taylor,Des Robinson,and David Cleland.Investigation of Ultimate Strength ofDeck Slabs in Steel-Concrete Bridges [J].Aci Structural Journal,2010,107 (1):82-91.
[12]Wang G,Q Wang and Z Li.Membrane action in lateral restraint reinforced concrete slabs[J].Journal of Central South University of Technology,2011,18 (2): 550—557.
[13]郑愚,李春红,Des.Rpnbison,Su.Taylor.混凝土桥面板中压缩薄膜效应的非线性有限元分析 [J].东莞理工学院学报, 2009 (3): 56-61.
[14]郑愚,潘云峰,于国友.交通荷载作用下压缩薄膜效应对GFRP筋混凝土桥梁面板工作性能的影响分析 [J].公路,2011 (4): 1-7.
[15]郑愚,李春红,秦怀泉.对GFRP筋混凝土桥面板中压缩薄膜效应的研究 [J].世界桥梁,2011(1):59-63.
Development History and Research Status Quo of Compressive Membrane Action in Concrete
GE Nan
Compressive membrane action (CMA)has been studied comprehensively in the article.The development of computing methods on CMA was discussed and compared to find out the most applicable theory basis.Combined CMA with contemporary building bridge,the further investigations and future research direction are proposed to satisfy modern structures and to get more economic effect.
compressive membrane action,arching action,concrete slabs,flexural capacity
U441
A
1008-3812(2017)03-004-03
2017-03-29
作者简介:葛楠 (1990— ),女,山西运城人,硕士研究生,助理工程师。研究方向:土木结构。

