梁方程降阶计算的重心插值配点法

徐子康，王兆清，*，孙浩森，李金

（1.山东建筑大学 工程力学研究所，山东 济南250101；2.山东建筑大学 学报编辑部，山东济南250101；3.山东建筑大学理学院，山东 济南250101）

梁方程降阶计算的重心插值配点法

徐子康1，王兆清1，*，孙浩森2，李金3

（1.山东建筑大学 工程力学研究所，山东 济南250101；2.山东建筑大学 学报编辑部，山东济南250101；3.山东建筑大学理学院，山东 济南250101）

采用重心插值配点法求解梁方程时，随着计算节点数量的持续增加，其计算精度将逐步下降。通过对降阶计算重心插值配点法的研究，可为数值求解梁方程提供一种数值稳定性好、计算精度高的新方法。文章基于重心Lagrange插值及其微分矩阵，推导了梁方程降阶计算重心插值配点法的公式，并通过数值算例验证其有效性。结果表明:随着计算节点数量的持续增加，降阶法的计算精度仍保持在10-10～10-12范围内；求解两端简支的梁方程时，两步降阶法的计算精度高于一步降阶法；直接法计算矩阵条件数与节点数的7次方是同阶的，而一步降阶法计算矩阵条件数与节点数的4次方是同阶的，降阶法可以有效地降低计算矩阵的条件数，提高计算精度；重心插值配点法采用矩阵—向量形式的计算公式，便于程序的编写，提高了计算效率。

梁方程；降阶法；重心Lagrange插值；配点法

0 引言

梁方程是工程技术领域中常见的四阶常微分方程。数值分析四阶常微分方程边值问题，按照微分方程离散方式的不同可分为Galerkin法［1-2］和配点法［3-4］。Galerkin法是基于加权积分表达的弱形式离散方法，其典型代表是有限元法。有限元法是一种低阶数值方法，要得到问题的高精度数值解，需要划分稠密的单元，这极大降低了分析问题的效率。有限元需要采用Galerkin法将控制微分方程离散为代数方程，在形成刚度矩阵过程中，需要进行大量的积分计算，而数值积分的精度将直接影响最终的计算结果。配点法是基于微分方程强形式的离散方法，也就是强迫微分方程在给定的离散节点上精确成立［5］。配点法是一种真正意义的无网格方法，其具有计算精度高、计算公式简单、不需要数值积分和程序实施方便等特点［6-8］。

利用配点法的诸多优点，国内外数值研究者采用不同的配点型方法求解四阶边值问题。Yogesh利用三次B样条函数近似未知函数，将计算区间采用等距节点离散，提出求解四阶边值问题的三次B样条配点法，其计算精度相比Siraj提出的五次非多项式样条配点法高1～3数量级［9］。Malek采用配点法将四阶常微分方程在计算区间上离散，利用拟谱法在每个子区域上近似未知函数，将提出的拟谱配点法应用于求解一维四阶线性微分方程、二维双调和方程和二维非矩形域问题［10］。Muite使用实空间微分法、谱空间预处理法、实空间积分法和谱空间积分法4种不同的Chebyshev配点法求解四阶边值问题，验证了不同方法下的计算精度和数值稳定性［11］。虽然学者基于配点法提出了多种求解梁方程的数值方法，但所提方法的计算公式繁琐，不便于程序的编写，因而计算精度和计算效率都比较低。

Lagrange插值在数值分析方面具有重要作用，但在等距节点插值过程中，当节点数量较大时，Lagrange插值表现出极大的数值不稳定性。采用Chebyshev或Legendre节点等特殊分布的插值节点可以显著提高Lagrange插值的稳定性和计算精度［12］。王兆清等将Lagrange插值公式改写成重心公式形式，提出了基于重心Lagrange插值的配点型数值方法—重心插值配点法（BICM）［6］。该方法首先是采用重心Lagrange插值近似未知函数并建立未知函数各阶导数在插值节点处的微分矩阵，然后利用微分矩阵直接离散梁方程和边界条件，最后求解矩阵形式的离散方程组。BICM采用矩阵—向量形式的计算公式，使得计算程序的编写非常方便，极大地提高了数值求解梁方程的计算精度和计算效率，现已广泛应用于求解微分方程的边值问题［13-15］、初值 问 题［16］和 初边 值 问题［17］。

采用重心插值配点法直接求解梁方程，随着计算节点数的持续增加，计算矩阵的条件数随之增大，其计算精度将逐步下降［5］。为了保证梁方程在不同计算节点数下的求解精度，文章在重心Lagrange插值配点法直接计算（直接法）的基础上，针对不同的边界条件，提出求解梁方程的一步降阶重心插值配点法（一步降阶法）和两步降阶重心插值配点法（两步降阶法）。两步降阶法的主要思想是先求出中间变量，再利用中间变量和未知函数的关系解出未知函数，实现两步重心插值配点法的降阶计算。一步降阶法将四阶梁控制微分方程表达为未知函数和中间变量的耦合微分方程组，利用重心插值配点法求解二阶耦合微分方程组。

1 重心Lagrange插值及其微分矩阵

考虑定义在区间 ［a，b］上的节点a＝x1＜x2＜… ＜xN＝b，函数w（x）在节点处的函数值为wi＝w（xi），i＝1，2，…，N。函数w（x）的重心Lagrange插值基函数由式（1）［5］表示为

重心Lagrange插值基函数 ξi（x）和重心插值权ωi分别由式（2）和（3）表示为

式中:k＝1，2，…，N；i＝1，2，…，N。

函数w（x）在节点处的m阶导数可由式（4）表示为

2 梁方程的重心插值配点法计算公式

2.1 求解梁方程的直接法

Euler-Bernoulli梁控制微分方程由式（5）表示为

式中:EI为梁的抗弯刚度；P为轴线方向上的荷载；f（x）为横向荷载。

两端简支的边界条件由式（6）表示为

两端固支的边界条件由式（7）表示为

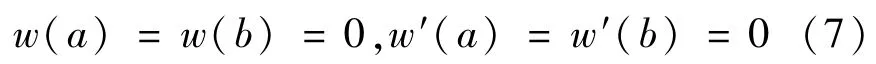
由重心Lagrange插值微分矩阵，式（5）的矩阵形式由式（8）表示为

式（8）可由式（9）简记为

式中:L＝EID（4）+PD（2）；w＝［w1，w2，…，wN］T；f＝（f（x1），f（x2），…，f（xN））T。

边界条件（6）或（7）采用重心插值公式（1）离散，则边界条件（6）或（7）的离散矩阵表达式可由式（10）表示为

将式（9）的主方程和式（10）的离散边界方程联立组合为一个过约束方程组，由式（11）表示为

上述边界条件的施加方法称为附加法，降阶法的边界条件也采用该方法作类似处理。采用最小二乘法求解方程组（11），得到未知函数在计算节点上的函数值。

2.2 简支边界条件下求解梁方程的两步降阶法

引进中间变量，中间变量由式（12）表示为

则式（5）、（6）表示的简支梁边值问题可分解为2个Poisson方程边值问题，分别由式（13）和（14）表示为

式（13）和（14）可采用重心插值配点法顺次求解，构成梁方程的两步降阶计算。两步降阶法相当于将原梁方程化为两个一维Poisson方程求解。由于边界条件必须是未知函数和中间变量的约束，两步降阶法仅适用于求解两端简支边界条件下的梁方程。对于一般边界条件下的梁方程，需采用一步降阶法求解。

2.3 一般边界条件下求解梁方程的一步降阶法

金属平衡管理是衡量冶炼企业工艺技术和管理水平的重要标志，通过计算金属回收率，反映金属元素的回收利用状况和损失方向[2]。

联立式（5）和（12），所得的方程组由式（15）表示为

采用重心插值微分矩阵离散方程（15），离散矩阵形式由式（16）表示为

采用附加法施加边界条件（10），得到的过约束代数方程组由式（17）表示为

一步降阶法将梁方程表达为未知函数和中间变量的耦合微分方程组，按照矩阵乘法的运算法则，通过增加分块零矩阵非常方便地施加各类边界条件，因而该方法不仅适用于求解两端固支边界条件下的梁方程，也可应用于求解任意边界条件（如简支和自由边界条件）下的梁方程。

3 数值算例

数值算例计算程序利用MATLAB编写，采用与第二类Chebyshev节点同分布形式的计算节点。直接法和一步降阶法的计算矩阵分别为L1和L2，相对误差由式（18）定义为

3.1 两端简支的梁方程

均布荷载作用下的简支梁，梁方程的边值问题由式（19）［5］表示为

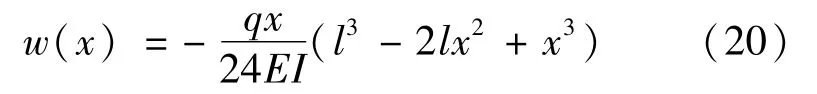
数值计算时，取梁的抗弯刚度EI＝106、l＝2、 q＝1000，一律采用国际制单位。直接法和两种降阶法计算的数据结果见表1。不同节点数计算的相对误差对数变化曲线如图1所示。

表1 直接法和降阶法计算矩阵条件数与计算的相对误差Er

图1 不同节点数计算的相对误差对数变化曲线图

观察图1可以发现，两步降阶法的计算精度最高，当节点数量在41个之内，3种方法的计算结果都保持在高精度范围内，随着节点数量的继续增加，直接法的计算精度不断下降，当节点数量增加到201时，直接法的计算结果没有意义而两种降阶法仍然能够得到高精度解。直接法和一步降阶法计算矩阵条件数与节点乘方的关系曲线如图2所示。

图2 直接法和一步降阶法计算矩阵条件数与节点乘方的关系曲线图

由图2可以直观的看出，随着节点数量的增加，直接法和一步降阶法计算矩阵的条件数不断增加，直接法计算矩阵条件数增长速度最快且增长曲线与N7基本吻合，一步降阶法计算矩阵条件数增长曲线与N4基本重合。计算矩阵的条件数越大，说明矩阵越病态，计算的精度就越低。图2中直接法计算矩阵迅速增加的条件数导致图1中直接法计算精度的持续下降，而一步降阶法可以极大地降低计算矩阵条件数从而得到更高的精度和更好的数值稳定性。

3.2 两端固支的梁方程

两端固支的梁方程边值问题由式（21）表示为

式（21）的解析解由式（22）表示为

梁方程（21）的边界条件为两端固支，采用直接法和一步降阶法进行求解。不同节点数计算的相对误差对数变化曲线如图3所示。直接法和一步降阶法计算的数据结果见表2。

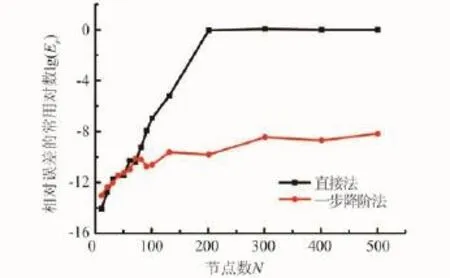
图3 不同数量节点计算的相对误差对数变化曲线图

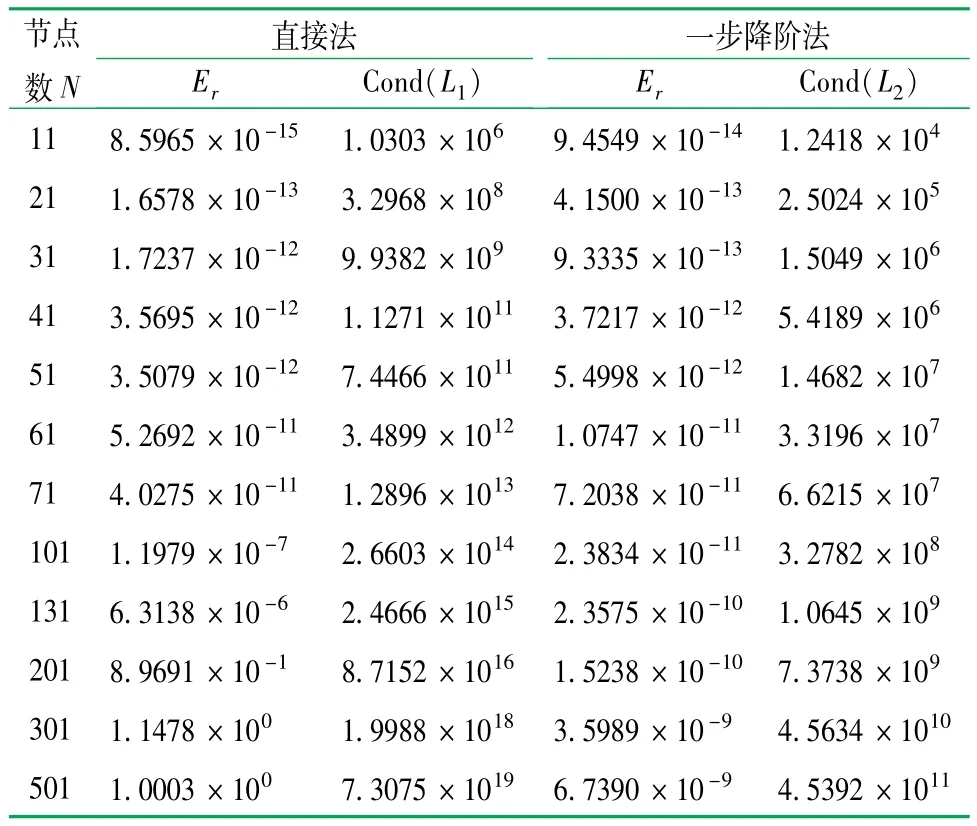
表2 直接法和一步降阶法计算矩阵条件数与计算的相对误差Er

观察图3发现，采用11个计算节点，直接法和一步降阶法即可得到问题的高精度解，当计算节点大于71时，直接法的计算精度迅速下降，而一步降阶法仍保持在高精度范围内。直接法和一步降阶法计算矩阵条件数与节点乘方的关系曲线如图4所示。

图4 直接法和一步降阶法计算矩阵条件数与节点乘方的关系曲线图

图4验证了直接法计算矩阵条件数与N7是同阶的，而一步降阶法计算矩阵条件数与N4是同阶的，进一步说明一步降阶法可以极大降低计算矩阵条件数，从而提高计算精度。

3.3 非齐次边界条件下的梁方程

梁方程边值问题由式（23）［10］表示为

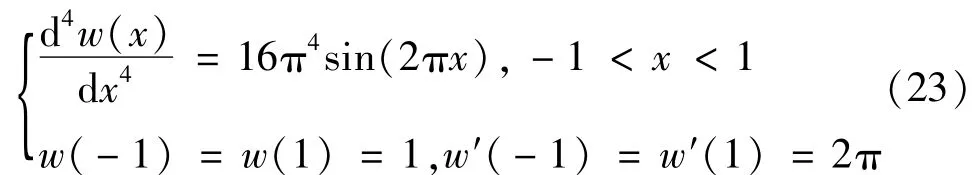
式（23）的解析解由式（24）表示为

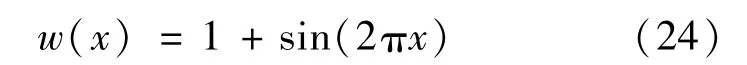
直接法和一步降阶法计算的数据结果见表3。不同数量节点计算的相对误差对数变化曲线如图5所示。

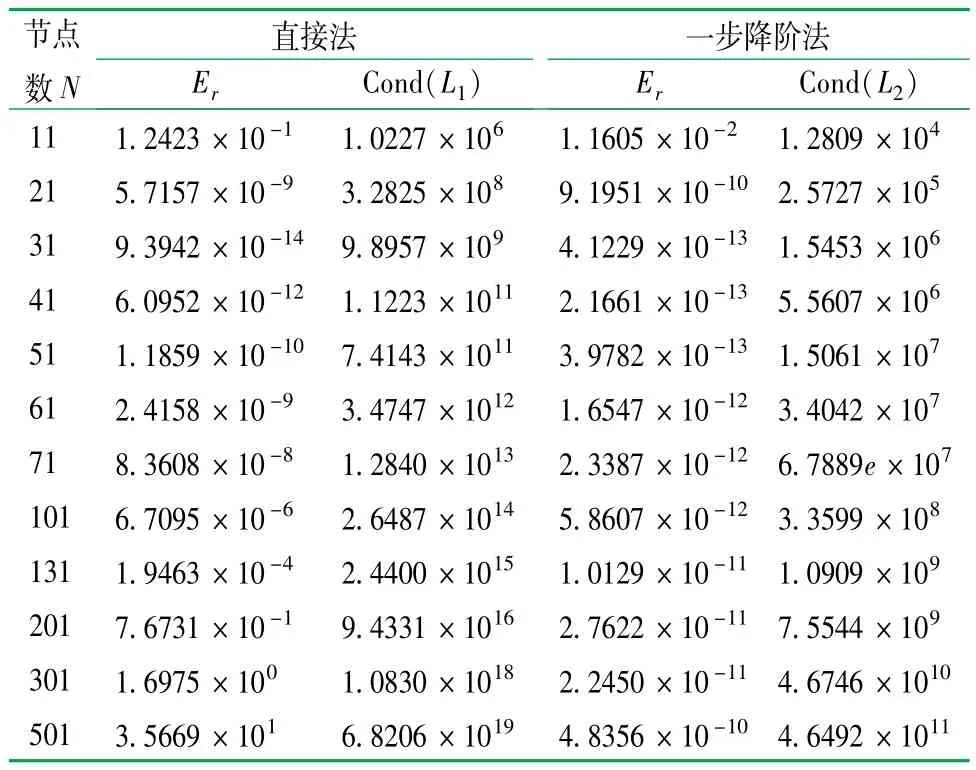
表3 直接法和一步降阶法计算矩阵条件数与计算的相对误差Er

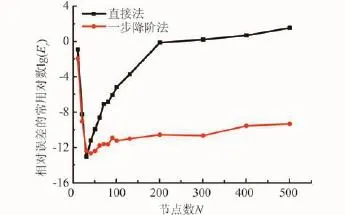
图5 不同数量节点计算的相对误差对数变化曲线图

观察图5可以发现，随着节点数的增加，直接法计算的误差曲线呈“V”字形，曲线下降段的原因主要是问题的解析解为三角振荡函数，采用较多的计算节点才能得到问题的高精度解；曲线上升段的原因是直接法计算矩阵的条件数迅速增加，导致直接法的计算精度持续下降。直接法和一步降阶法计算矩阵条件数与节点乘方的关系曲线如图6所示。

图6 直接法和一步降阶法计算矩阵条件数与节点乘方的关系曲线图

图6中的关系曲线再次得出了与图2和4相同的结论，进一步验证了一步降阶法可以明显降低计算矩阵条件数，从而提高计算精度。

4 结论

通过上述研究表明:

（1）数值求解四阶梁方程，随着计算节点数量的持续增加，直接法的计算精度逐步下降，直至失去数值意义，而一步降阶法和两步降阶法的计算精度仍保持在10-10～10-12。相比直接法，降阶法具有更高的计算精度和更好的数值稳定性。

（2）由于边界条件必须是未知函数和中间变量的约束，两步降阶法仅适用于求解两端简支边界条件下的梁方程。求解两端简支的梁方程时，两步降阶法的计算精度高于一步降阶法。

（3）求解梁方程时，计算矩阵的条件数与节点数存在着明显的数量关系:直接法计算矩阵条件数与N7是同阶的，而一步降阶法计算矩阵条件数与N4是同阶的。这说明一步降阶法能够通过降低求导的阶数，有效降低计算矩阵的条件数，从而明显改善计算精度。

（4）采用重心Lagrange插值微分矩阵离散四阶梁控制微分方程，使得控制方程的离散过程非常简便和直接。矩阵—向量形式的计算公式，非常适用于MATLAB计算程序的编写，极大地提高了数值求解的效率。重心插值配点法的计算公式简单，程序实施方便，是一种高精度的无网格数值分析方法。

［1］ Arnold D.N.，Awanou G.，Qiu W.，etal..Mixed finite elements for elasticity on quadrilateral meshes［J］.Advances in Computational Mathematics，2015，41（3）:553-572.

［2］ Atluri S.N.，Liu H.T.，Han Z.D.，et al..Meshless local petrov-Galerkin（MLPG）mixed collocation method for elasticity problems［J］.Cmes-computer Modeling in Engineering＆Sciences，2006，4（3）:141-152.

［3］ Kruse R.，Nguyenthanh N.，De Lorenzis L.，etal..Isogeometric collocation for large deformation elasticity and frictional contact problems［J］.Computer Methods in Applied Mechanics and Engineering，2015，296（1）:73-112.

［4］ Stevens D.，Power H.，Cliffe K.A.，et al..A meshless local RBF collocationmethod using integral operators for linear elasticity ［J］.International Journal ofMechanical Sciences，2014，88（1）: 246-258.

［5］ 李树忱，王兆清.高精度无网格重心插值配点法——算法、程序及工程应用［M］.北京:科学出版社，2012.

［6］ 王兆清，唐炳涛，李树忱，等.求解间断边值问题的重心插值单元配点法［J］.山东建筑大学学报，2009，24（2）:115-118.

［7］ 李树忱，王兆清，袁超.极坐标系下弹性问题的重心插值配点法［J］.中南大学学报（自然科学版），2013，44（5）:2031-2040.

［8］ 王兆清，庄美玲，姜剑.非线性MEMS微梁的重心有理插值迭代配点法分析［J］.固体力学学报，2015，36（5）:453-459.

［9］ Yogesh G.，Manoj K..Numerical Method for Solving Boundary Value Problem Arising in Deflection of Beams［J］.Canadian Journal on Computing in Mathematics，Natural Sciences，Engineering and Medicine，2011，2（7）:166-169.

［10］Malek A.，Phillips T.N..Pseudospectral collocation methods for fourth-order differential equations［J］.IMA Journal of Numerical Analysis，1994，15（4）:523-553.

［11］Muite B.K..A numerical comparison of Chebyshev methods for solving fourth order semilinear initial boundary value problems ［J］.Journal of Computational and Applied Mathematics，2010，234（2）:317-342.

［12］Weideman J.A.，Reddy S.C..A MATLAB differentiation matrix suite［J］.ACM Transactions on Mathematical Software，2000，26 （4）:465-519.

［12］王兆清，唐炳涛，李树忱，等.求解间断边值问题的重心插值单元配点法［J］.山东建筑大学学报，2009，24（2）:115-118，123.

［14］王兆清，李淑萍，唐炳涛.圆环变形及屈曲的重心插值配点法分析［J］.机械强度，2009，31（2）:245-249.

［15］王兆清，綦甲帅，唐炳涛.奇异源项问题的重心插值数值解［J］.计算物理，2011，28（6）:883-888.

［15］李淑萍，王兆清，唐炳涛.重心插值配点法求解初值问题［J］.山东建筑大学学报，2007，22（6）:481-485，506.

［17］王兆清，马燕，唐炳涛.梁动力学问题重心有理插值配点法［J］.振动与冲击，2013，32（22）:41-46.

（学科责编：赵成龙）

Barycentric interpolation collocation method based on depression of order for solving beam equations

Xu Zikang1，Wang Zhaoqing1，*，Sun Haosen2，et al.
（1.Institute of Mechanics，Shandong Jianzhu University，Jinan 250101，China；2.Editorial Department of Journal of Shandong Jianzhu University，Jinan 250101，China）

When the beam equations are solved by barycentric interpolation collocation method，computational accuracy will decline gradually as the number of nodes increases.The research on barycentric interpolation collocationmethod based on depression of order，can provide the new method that has a good numerical stability and high computational accuracy for beam equations.Based on barycentric Lagrange interpolation and its differentialmatrices，the formula of barycentric interpolation collocationmethod based on depression of order is derived.Numerical examples are given to verify the effectiveness of the proposed method.The result shows that the computational accuracy of depression of ordermethod remains the range of10-10～10-12as the number of nodes increases.When the beam equations with simply supported ends are solved，the computational accuracy of the two-step depression of order method is higher than the one-step depression of order method.The condition number of the directmethod is close to 7th power of the number of nodes，and the condition number of one-step depression of ordermethod is close to 4th power of the number of nodes.The depression of ordermethod can effectively reduce the condition number of computingmatrix such that improves the computational accuracy.By applying the computational formula with matrix-vector form，the program is easy to write and the computational efficiency of barycentric interpolation collocationmethod can beimproved remarkably.

beam equations；depression of order method；barycentric Lagrange interpolation；collocation method

O302

A

1673-7644（2017）03-0245-06

2017-04-25

国家自然科学基金面上项目（51379113）；国家自然科学基金项目（11471195）；山东省自然科学基金重点项目（ZR2016JL006）

徐子康（1993-），男，在读硕士，主要从事工程数值分析方法等方面的研究.E-mail:xuzikang1993＠163.com

*：王兆清（1965-），男，副教授，博士，主要从事工程数值分析方法等方面的研究.E-mail:sdjzuwang＠126.com