基于QC-LDPC码的联合信源信道编码研究

王海丽,黎 勇

(重庆邮电大学 重庆市移动通信技术重点实验室，重庆 400065)

基于QC-LDPC码的联合信源信道编码研究

王海丽,黎 勇

(重庆邮电大学 重庆市移动通信技术重点实验室，重庆 400065)

基于欧式几何构造的准循环LDPC码(quasi-cyclic LDPC，QC-LDPC)应用于联合信源信道编码(joint source and channel coding，JSCC)系统中，由于JSCC系统中信源码和信道码存在特殊的边连接关系，致使满足信源码字和信道码字之间特殊连接关系的QC-LDPC码字比较少，但至少QC-LDPC码可以用来作为JSCC系统中的信道码。仿真结果表明，双QC-LDPC码的JSCC系统纠错性能相比双随机LDPC码的JSCC系统有明显的改善，同时前者的译码迭代次数明显少于后者，从而提升了译码效率。仅使用QC-LDPC码作为信道码的JSCC系统也比双随机LDPC码的JSCC系统有更好的性能，且其迭代次数也更少。

联合信源信道编码；低密度奇偶校验码；准循环低密度奇偶校验码

0 前 言

随着通信技术的发展进步，无线多媒体通信技术越来越受到重视。信源编码与信道编码分开设计的通信系统，已经无法满足人们对通信质量和通信效率的高要求。对通信质量要求很高的场景，比如医疗图像传输，若传输信息有误，会导致医生做出错误的判断，给患者带来不可避免的伤害。

通信系统中，分开设计信源编码和信道编码的方案，导致了信源编码后的冗余信息不能被充分利用来进行解码，造成了信源资源的浪费。许多学者开始研究联合信源信道编码的设计方案。文献[1]提出了基于信源压缩格式(JPEG2000)的联合信源信道编码方案，该方案根据信源压缩后码流的特点进行信道译码，提高了传输效率。García-Frias等[2]基于隐型马尔科夫信源和Turbo码型设计了联合信源信道编码方案，García-Frias等[3]又将该方案扩展到LDPC码并提出了基于LDPC码的联合信源信道编码方案，M.Fresia等[4]在此基础上提出基于双随机LDPC码的JSCC系统。

Huihui Wu等[5-6]将文献[7]中提出的基于原模图LDPC码的JSCC系统应用于实际的医疗摄影图像传输中，相比于传统的图像传输系统，该系统没有压缩格式的限制，性能更优，同时降低了复杂度。尽管双随机LDPC码的JSCC系统在图像传输方面表现出了明显的优势，但为了能够适应无线传输的环境，发送端和接收端的系统框架还需要进一步优化。对于信道带宽固定的JSCC系统，文献[8]提出一种信源和信道码率自适应分配的方案。该方案是根据信道的状态信息和信源的统计特征来自适应地分配信源码率和信道码率。仿真结果表明，该方案可以同时具有良好瀑布区性能和错误平台性能。

本文根据文献[9]中的方法构造出基于欧式几何的QC-LDPC码，并将其应用于JSCC系统中。仿真结果表明，基于QC-LDPC码的JSCC系统相比于基于随机LDPC码的JSCC系统，前者不仅可以获得更好的纠错性能，而且达到译码收敛所需的迭代次数更少，从而提升了译码效率。

1 JSCC系统简介

1.1 JSCC系统的编码过程

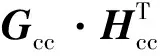
假设Hsc矩阵为l×n，Hcc矩阵为(m-l)×m，则信源压缩码率为Rsc=l/n，信道编码码率为Rcc=l/m，整个JSCC系统的码率为R=Rcc/Rsc=n/m。

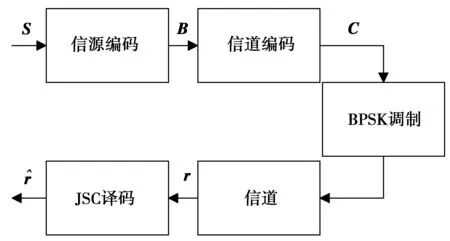
图1 双LDPC码的JSCC系统框图Fig.1 System model of JSCC based on LDPC code

1.2JSCC系统的译码过程

为了方便分析JSCC系统的译码过程，图2给出了JSCC系统中双LDPC码的Tanner因子图。图2中，左半部分表示信源LDPC码的因子图，右半部分表示信道LDPC码的因子图。信源LDPC码和信道LDPC码的因子图中相互连线的部分为二者信息交互的纽带，信道译码过程和信源译码过程通过这些连线传递似然信息。

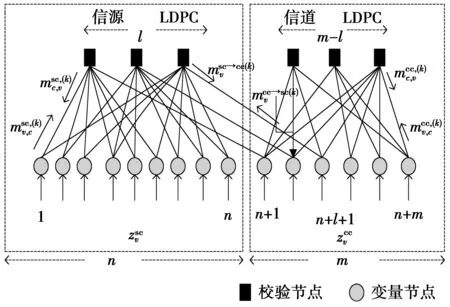
图2 JSCC系统中双LDPC码的Tanner图Fig.2 Tanner diagram of JSCC system based on LDPC code

图2中用到的变量定义如下

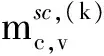
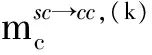
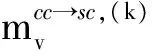
根据LDPC码的SPA译码算法，图2中Tanner图的变量节点向校验节点间传递似然信息的迭代过程为

(1)

(2)

(3)

(4)

(1)式中，v=1,2,…,n；(2)式和(3)式中，v=n+1,n+2,…,n+l；(4)式中，v=n+l+1,n+l+2,…,n+m。

校验节点向变量节点传递似然信息的迭代过程为

(5)

(6)

(7)

(5)～(6)式中，c=1,2,…,l；(7)式中，c=l+1,2,…,m。

经过k次迭代译码后，信源信息被估计，其公式为

(8)

(8)式中，L(Sv)的计算公式为

(9)

2 QC-LDPC码矩阵构造

QC-LDPC码是LDPC码的一个子类[10]，具有循环和准循环的特性。性能良好的LDPC码，具有较大的最小汉明距离和围长。本文首先利用欧式几何中的相交线构造一个大围长的基础矩阵，然后在给定的有限域范围内扩展成LDPC码的奇偶校验矩阵，同时使其具有循环和准循环的特性。下面将详细介绍基于欧式几何构造QC-LDPC码的过程。

假设有一个n维向量(m0,m1,…,mn-1)，其分量元素mi(i=0,1,…,n-1)的取值范围属于伽罗华域GF(2s)，即mi有2s个取值，则这样的n维向量总共存在2ns个。在几何数学中，这2ns个n维向量就构成了GF(2s)的向量空间，即构成了伽罗华域GF(2s)上的n维欧式几何，简称EG(n,2s)。

在EG(n,2s)中，任何一个n维向量都是几何体中的一个点，几何体中总共存在2ns个点，全零n维向量为几何体中的原点。若a0为EG(n,2s)中的一个点，那么过该点的直线有k=(2ns-1)/ (2s-1)条，每条直线中都包含2s个点。EG(n,2s)中的每条直线有2(n-1)s-1条平行线，故EG(n,2s)中直线的总数为k(2(n-1)s-1)。任意2条直线，它们要么平行，要么相交。利用欧式几何中的相交线可以将整个伽罗华域GF(2ns)划分为k个不同的子集，每个子集代表一簇平行线集合。令α为GF(2s)中本原元素，β为GF(2ns)中本原元，则GF(2s)中的2s个元素为α-∞=0,α0,…,α2s-2，EG(n,2s)中所有元素为β-∞=0,β0=1,β,…,β2ns-2。

假设a0和a1为EG(n,2s)中线性独立的2个点，则通过点a0和a1的直线为

(10)

设点a2是EG(n,2s)中与a0和a1均相互独立的点，则通过点a0和点a2的直线为

(11)

显而易见，直线l1和直线l2相交于点a0。令βil1(β∈GF(2ns))，文献[11]已经证明βil1仍为欧式几何EG(n,2s)中的线，相当于对直线l1在有限域范围内进行了循环移位。由此可以得到QC-LDPC码的基础矩阵B，对基础矩阵B进行本地向量扩展就得到矩阵QEG，再对QEG进行转置，就得到了QC-LDPC码的奇偶校验矩阵H。

基础矩阵B可表示为(T表示矩阵转置)

(12)

(12)式中，Mi(i=1,…,k-1)表示为

(13)

(13)式中，li表示为

(14)

将Mi矩阵进行本地向量扩展得到

(15)

(15)式中，Bi,j是由向量

进行本地向量扩展得到的分块，每个分块的大小为(2ms-1)×(2ms-1)，则将B矩阵进行本地向量扩展以后的形式为

(16)

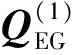
3 QC-LDPC码在JSCC系统的应用

由第2节中的奇偶校验矩阵的构造方式可知，最后生成的QC-LDPC码的奇偶校验矩阵有很大的随机性，故QC-LDPC码的码长不是能够人为控制的。由1.1节介绍的JSCC系统可知，信源经过压缩后的信息长度，决定了输入信道进行信道编码的信息长度。而信源压缩的长度是由信源LDPC码的奇偶校验矩阵的行数决定的。

若要信源编码和信道编码能够同时使用QC-LDPC码，则产生的两个检验矩阵必须满足上述约束条件。满足上述约束条件信源码的矩阵为181×504，信道码的矩阵为29×210。当不能产生同时满足信源编码和信道编码的奇偶校验矩阵时，则仅将QC-LDPC码用在信道编码部分，信源码用随机LDPC码。由此产生的信道码矩阵有1 522×3 066和231×1 026的QC-LDPC码，它们对应的信源矩阵大小分别为1 544×3 600和1 029×4 166。图3的仿真结果为不同码长的QC-LDPC码和随机LDPC码的错误平台性能对比图。由图可知，QC-LDPC码相比同等长度的随机LDPC码通常具有更好的纠错性能或者更低的错误平台。

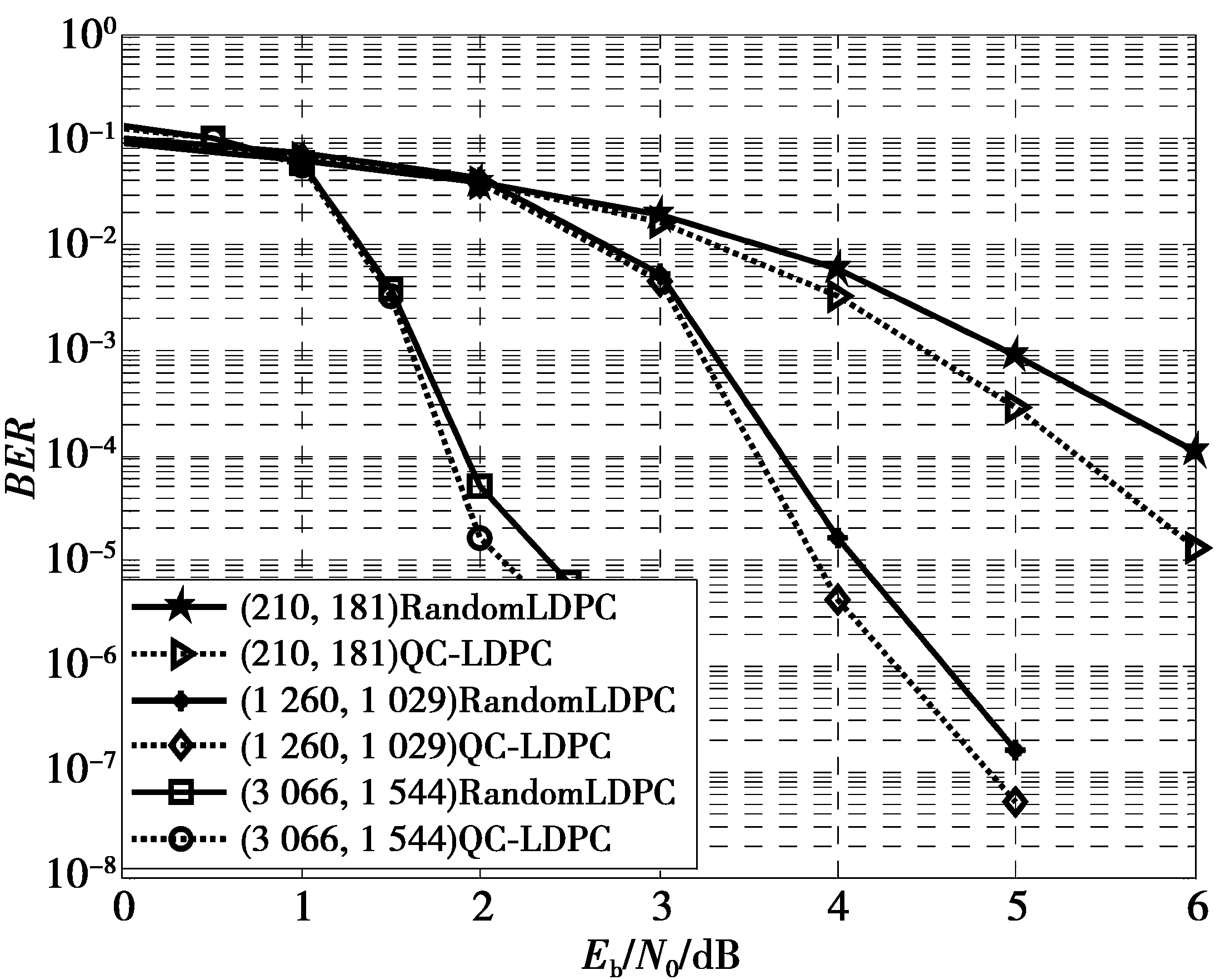
图3 QC-LDPC码和随机LDPC码的误比特率 性能对比Fig.3 BER comparison of QC-LDPC codes and LDPC codes with different code length

4 仿真结果分析

本文中做了3个仿真。实验采用C语言编程，仿真平台为VS2010，仿真信道为加性高斯白噪声信道。所采用的信源均为独立同分布伯努利信源，信源产生1的概率为0.02。在第1和第2个仿真中信源码字均为随机LDPC码，信道码字分别为基于欧式几何产生的QC-LDPC码和随机LDPC码。第1个试验中，信源矩阵大小为1 029×4 166，相应的码率为0.25，信道矩阵大小为231×1 260，其码率为0.82；第2个实验中，信源矩阵大小为1 544×3 600，其码率为0.43，信道矩阵大小为1 522×3 066，相应的码率为0.504，仿真结果如图4所示。第3个仿真中，恰好能够构造出2个同时满足信源码字与信道码字之间特殊连接关系的QC-LDPC码，该信源矩阵大小为181×504，信源码率为0.36，信道矩阵大小为29×210，信道码率为0.86。该仿真中，对于信源码字和信道码字采用QC-LDPC码和随机LDPC码的组合或者二者均采用随机LDPC码的每种情况都进行了仿真，结果如图5所示。

由图4中仿真结果可知，在信源码率较高时，信源存在的冗余信息少，使用低码率的随机LDPC码作为信道码，JSCC系统就能达到良好的性能。若将信道码换成QC-LDPC码，在低信噪比下，系统性能基本保持不变，但在高信噪比下，在BER为10-8时性能改善了约0.34 dB。

图4 2种信道码型在JSCC系统中的 BER性能曲线图Fig.4 BER performance of two kinds of channel codes in JSCC system

图5 在Rsc=0.36,Rcc=0.86 JSCC系统中 4种情况下的误码率性能Fig.5 BER Performance of four possible cases in JSCC system with Rsc=0.36 and Rcc=0.86

由图5可知，用双QC-LDPC码代替双随机LDPC码后，整个系统的性能有明显的改善，在BER为10-4时改善了约2.9 dB。若单独用QC-LDPC码作为系统的信源码或者信道码，得到的系统性能也均优于传统的基于双随机LDPC码的JSCC方案。

QC-LDPC码的奇偶校验矩阵和生成矩阵具有循环或准循环的特性，这种结构使其编码结构简单，译码复杂度低。图6给出了第3个仿真中分别基于双QC-LDPC码和双随机LDPC码的JSCC系统在不同信噪比条件下，译一个码字的平均迭代次数。由图6可知，在低信噪比下，双随机LDPC码的JSCC系统的译码迭代次数要多于双QC-LDPC码的JSCC系统。

图6 JSCC系统在2种码型下的译码迭代次数Fig.6 Decoding iteration number of JSCC system under two kinds of code

图7给出了第一个仿真和第二个仿真中双随机LDPC码的JSCC系统和仅在信道编码部分使用QC-LDPC码的JSCC系统，在不同信噪比下，译一个码字的平均迭代次数。由图7可知，在低信噪比下，信源码率越高，平均译码迭代次数越少。在同一信源码率时，双随机LDPC码的JSCC系统的平均译码迭代次数更多。

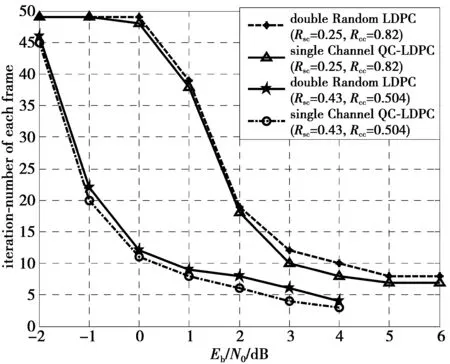
图7 JSCC系统在2种信道码型下的译码迭代次数Fig.7 Decoding iteration number of JSCC system under two kinds of channel codes

5 结 论

本文主要研究了基于欧式几何构造的准循环LDPC码的JSCC系统性能，并对其译码复杂度进行了分析。由前面的仿真结果可知，双QC-LDPC码的JSCC系统相比于传统的双随机LDPC码的JSCC系统，瀑布区性能和错误平台区性能均有不同程度的改善。在未来的工作中，可以考虑进一步优化其边连接关系，从而进一步提升JSCC系统的性能。

[1] PU L, WU Z, BILGIN A, et al. LDPC-based iterative joint source-channel decoding for JPEG2000[J]. IEEE Transactions on Image Processing a Publication of the IEEE Signal Processing Society, 2007, 16(2):577-81.

[2] GARCIA F J, VILLASENOR J D. Combining hidden Markov source models and parallel concatenated codes [J]. IEEE Communications Letters, 1997, 1(4):111-113.

[3] GARCIA F J, ZHONG W. LDPC codes for compression of multi-terminal sources with hidden Markov correlation [J]. IEEE Communications Letters, 2003, 7(3):115-117.

[4] FRESIA M, PEREZ C F, POOR H V. Optimized Concatenated LDPC Codes for Joint Source-Channel Coding[C]// IEEE International Conference on Symposium on Information Theory.USA:IEEE Press,2009:2131-2135.

[5] WU H, HE J, XU L, et al. Joint Source-Channel Coding Based on P-LDPC Codes for Radiography Images Transmission[C]// IEEE, International Conference on Trust, Security and Privacy in Computing and Communications. USA: IEEE Press, 2012:2035-2039.

[6] XU L, WU H, HE J, et al. Unequal error protection for radiography image transmission using protograph double LDPC codes[C]// Wireless Telecommunications Symposium. USA: IEEE, 2013:1-5.

[7] HE J, WANG L, CHEN P. A joint source and channel coding scheme base on simple protograph structured codes[C]// Communications and Information Technologies(ISCIT), 2012 International Symposium on. USA: IEEE, 2012:65-69.

[8] CHEN C, WANG L, JIANG Z. Adaptive Rate Allocation Scheme for Joint Source-Channel Coding Based on Double Protograph LDPC Codes[C]// Wireless Personal Multimedia Communications (WPMC),2014International Symposium on. USA: IEEE, 2014:158-162.

[9] TAI Y Y, LAN L, ZENG L, et al. Algebraic construction of quasi-cyclic LDPC codes for the AWGN and erasure channels[J].IEEE Transactions on Communications,2006, 54(10):1765-1774

[10] LIU K, El K M, LEE J. Finite-Length Algebraic Spatially-Coupled Quasi-Cyclic LDPC Codes [J]. IEEE Journal on Selected Areas in Communications, 2016, 34(2):329-344.

[11] TANG H, XU J, LIN S, et al. Codes on finite geometries [J]. IEEE Transactions on Information Theory, 2005,51(2):572-596.

(编辑：张 诚)

s：The National Natural Science Foundation of China (61401050); The Science and Technology Project of Chongqing Municipal Education Commission of China (KJ1400425)

In this paper, quasi cyclic low density parity check (QC-LDPC) codes based on Euclidean geometry are applied into the JSCC system. Since there are special links between the source code and the channel code in the JSCC system, it is difficult to construct two QC-LDPC codes which can be applied into the JSCC system. However, at least we can use a QC-LDPC code as the channel code in the JSCC system. Simulation results show that the performance of the JSCC system based on double QC-LDPC codes is significantly improved compared to that of the JSCC system based on the double random LDPC code, and the decoding iteration number of the former is obviously less than that of the latter, and thus improves the decoding effectively. The JSCC system just only using QC-LDPC code as the channel code performs better than that based on double random LDPC codes, and it also requires less iteration.

joint source and channel coding; low density parity check code; QC-LDPC code

2016-09-23

2016-11-17 通讯作者：黎 勇 yongli@cqupt.edu.cn

国家自然科学基金(61401050)；重庆市教委科技项目(KJ1400425)

10.3979/j.issn.1673-825X.2017.04.008

TN911.22

A

1673-825X(2017)04-0474-06

Research on joint source and channel coding based on QC-LDPC code

(Key Lab of Mobile Communication Technology in Chongqing, Chongqing University of Posts and Telecommunications,Chongqing 400065 P.R.China)

王海丽(1990-),女，河南人，硕士研究生。主要研究方向为信道编译码理论。E-mail:whl_0125@163.com。

黎 勇(1982-)，男，重庆人，博士，讲师。主要研究方向为信息论与编码，无线移动通信。E-mail: yongli@cqupt.edu.cn。

WANG Haili, LI Yong