一类随机Burgers方程的奇摄动解

洪文珍,包立平

(杭州电子科技大学数学研究所,浙江 杭州 310018)

一类随机Burgers方程的奇摄动解

洪文珍,包立平

(杭州电子科技大学数学研究所,浙江 杭州 310018)

讨论了一类随机Burgers方程的奇摄动解，其噪声项服从弱噪声Ornstein-Uhlenbeck(O-U)过程，并构造了相应的形式渐近解.通过摄动分析得到波的期望和初值条件，并通过余项估计得到渐近解的有效性.

奇摄动；随机Burgers方程；平均速率；Ornstein-Uhlenbeck过程；一致有效估计

0 引 言

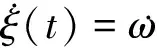
本文中，在α≠1条件下，考虑一类在有色噪声影响下的随机Burgers方程，且其噪声项服从弱噪声Ornstein-Uhlenbeck(O-U)过程，首先对所构造的波运动的平均速率方程和相应初值条件所满足的Kolmogorov方程，进行奇摄动展开，得到相应的Kolmogorov方程和Burgers方程的形式渐近解，并证明了形式渐近解的存在性与有界性；又通过余项估计，求得波运动平均速率的渐近解和初值条件的渐近解.

1 模型建立

设波的运动轨迹u(t,x)满足随机微分方程

(1)

其中，α是常数，ε是小参数.

假设：

1)a(t,x)，b(t,x)是已知的任意阶连续可微函数且均不为0；

2)ψ在R上有界，φ0(q)亦有界；

3)QT=[0,T]×R，∂PQT为QT区域的边界.

根据文献[7]可知，式(1)的解满足

(2)

(3)

令v(t,x)=Ex,tg(s,y)=∫g(s,y)p(t,x,s,y)dy，可得v(t,x)满足的后向Kolmogorov方程：

(4)

2 形式展开

2.1 初值条件的形式渐近解

首先对式(2)作形式渐近展开，得到：

(5)

关于ε作摄动展开，并比较ε的同次幂系数，可得：

(6)

(7)

⋮

(8)

⋮

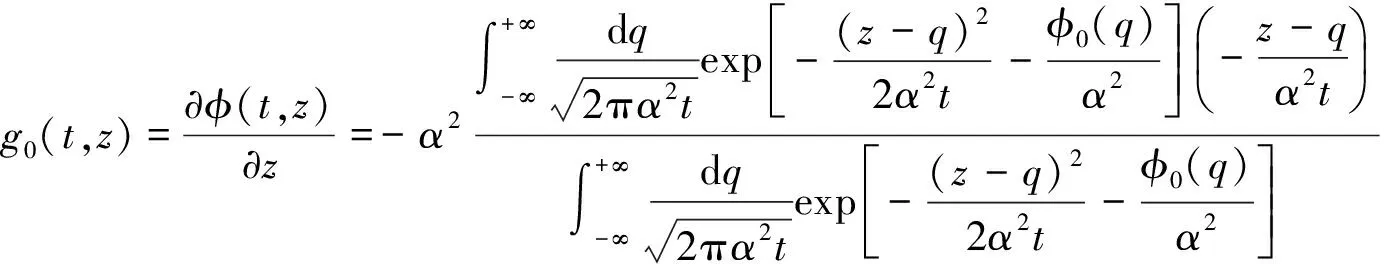
知g0z有界.

下面讨论式(7)，首先构造一个泛函

(9)

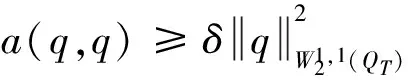
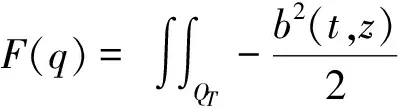
g0zzqte-θ tdtdz，恒存在唯一的g1∈H，使得F(q)=a(g1,q)，对于任意给定的q∈H，所以式(7)的解存在唯一，即g1可解.

类似情况下，可得g2,g3,…,gn,…的解存在唯一性，从而得到式(2)的形式渐近解.

2.2 平均速率的形式渐近展开

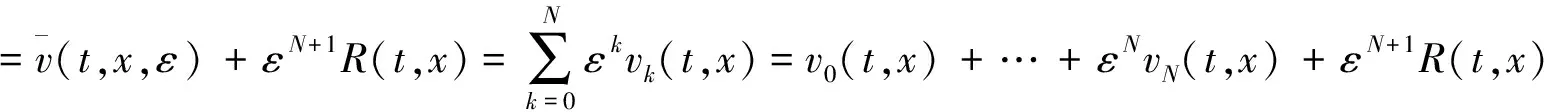
关于ε作摄动展开，并比较ε的同次幂系数可得：

(10)

(11)

⋮

(12)

⋮

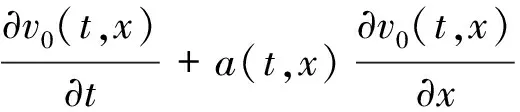
φ(x-∫a(t,x)dt)=0

其中，φ(x)为x的任意连续可微函数.考虑到v0(t=s,x)=g0，其中g0为已知函数，所以可得v0(t,x).

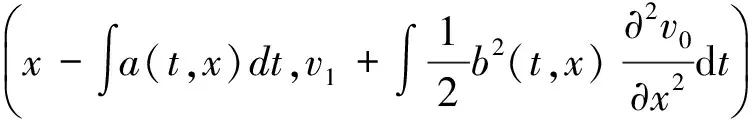
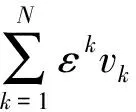
3 余项估计

3.1 初值条件的余项估计

首先考虑式(2)的余项

(13)

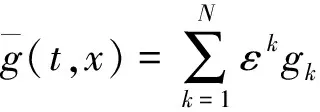
(14)

其中，H(t,x)为已知函数.

令R1=eλtP，其中λ>0，式(14)转化为：

(15)

令

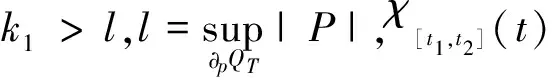
在式(15)两边同时乘以检验函数φ，且取积分，可得

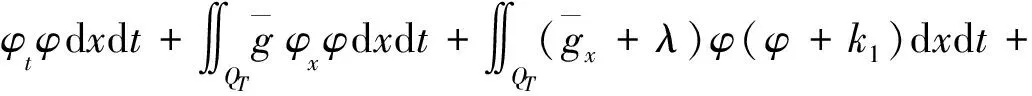
(16)

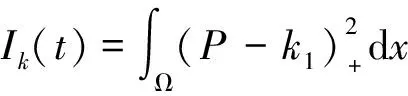
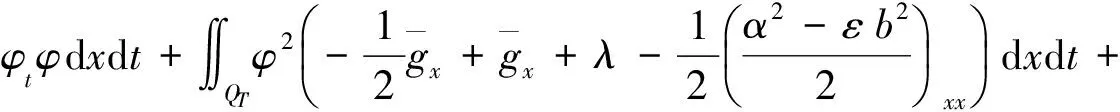
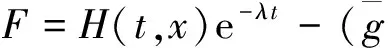
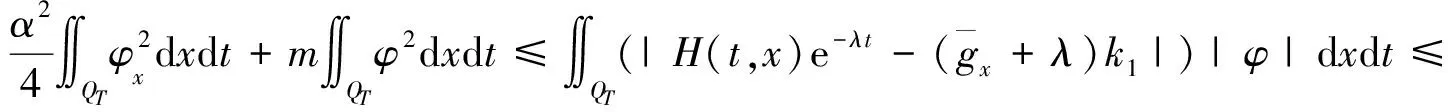
由嵌入定理与Holder不等式，可得

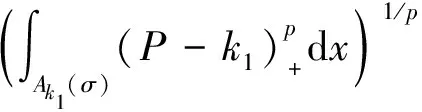
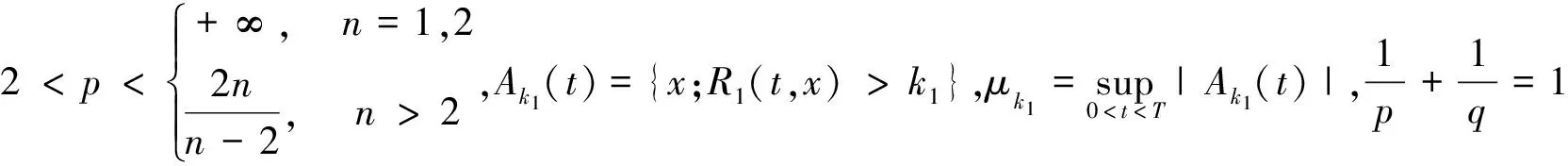
对于任何h>k1,t∈[0,T]，有Ah(t)⊂Ak1(t).

所以，

注意到，

可得

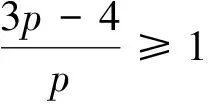
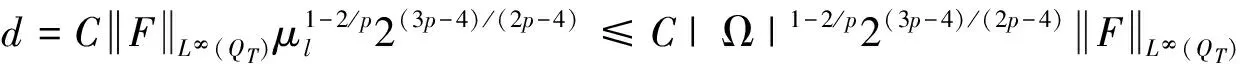
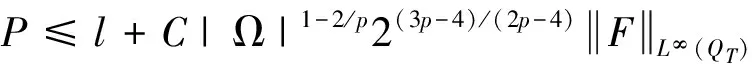
因此，R1的有界，即式(14)一致有效.

3.2 平均速率的余项估计

同理，考虑式(4)的余项

(17)

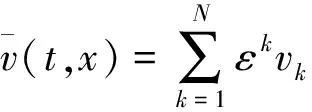
(18)

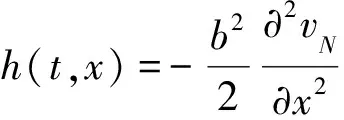
令R2=φeλs，其中λ>0.所以式(18)可以化简为

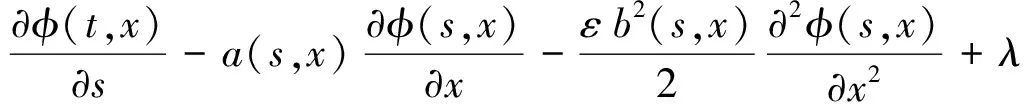
(19)

令

(20)

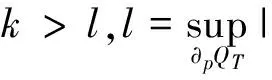
在式(20)两边同时乘上检验函数φ，并取积分，可得

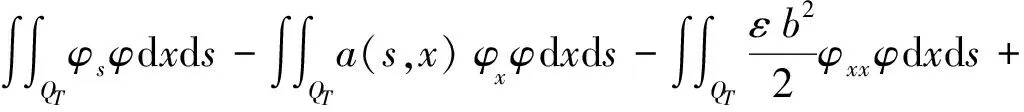
令

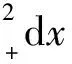
则Ik(s)于[0,T]上绝对连续.

所以，式(19)化简为，

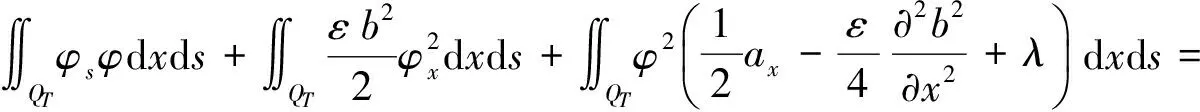
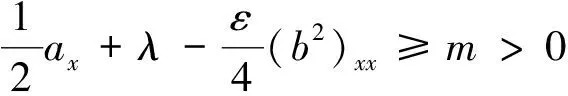
∬QTmφ2dxds≤∬QT(-he-λs-kλ)φdxds≤0，所以φ几乎处处为零.即φ≤k，所以，R2有界.

4 结束语

α≠1条件下，本文讨论了一类在有色噪声影响下的随机Burgers方程，其波动率服从弱噪声O-U过程.考虑奇摄动随机Burgers方程在无界区域上的波运动的初值条件和平均速率的形式渐近解，并应用相关的极值原理、Lax-Milgram定理和De Giorgi迭代技术证明其存在性、有界性和一致有效性.将进一步研究随机Burgers方程在有界区域上的形式渐近解问题.

[1]WADATI M． Stochastic Korteweg-de Vries equation[J]. Journal of the Physical Society of Japan, 1983,52(8):2642-2648.

[2]LILLO S D. The Burgers equation under multiplicative noise[J]. Physics Letters A, 1994,188(4/5/6):305-308.

[3]CHEKHLOV A, YAKHOT V. Kolmogorov turbulence in a random-force-driven Burgers equation[J]. Physical Review E Statistical Physics Plasmas Fluids & Related Interdisciplinary Topics, 1995,51(4):5681-5684.

[4]Weinane， Eric Vanden Eignden． Statistical Theory for the Stochastic Burgers Equation in the Inviscid Limit[J]． Communications on Pure and Applied Mathematics，2000,53(7)：852-901.

[5]VILLARROEL J. The Stochastic Burger’s Equation in Ito’s Sense[J]. Studies in Applied Mathematics, 2004,112(1):87-100.

[6]VILLARROEL J. Stochastic Perturbations of Line Solitons of KP[J]. Theoretical and Mathematical Physics, 2003,137(3):1753-1765.

[7]司曲斯.随机微分方程理论及其应用[M].上海：上海科学技术文献出版社,1986：102-120.

[8]伍卓群,尹景学,王春朋.椭圆与抛物型方程引论[M].北京：科学出版社,2003：44-85.

Asymptotic Solution of a Class of Stochastic Burgers Equation

HONG Wenzhen, BAO Liping

(InstituteofMathematics,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

In this paper, the singular perturbation solution for a class of stochastic burgers equation is discussed. Its volatility is subject to the weak noise Ornstein-Uhlenbeck(O-U) process. The corresponding asymptotic solution is constructed. By the perturbation analysis, the wave expectationv(t,x) and the initial conditiong(t,x) are obtained. And the uniformly valid estimate for the asymptotic solution of the system is obtained.

singular perturbation; random Burgers equation; average velocity; Ornstein-Uhlenbeck process; uniformly valid estimate

10.13954/j.cnki.hdu.2017.04.021

2016-11-02

国家自然科学基金项目(51175134)

洪文珍(1991-)，女，安徽安庆人，硕士研究生，偏微分方程.通信作者：包立平副教授，E-mail:baolp@hdu.edu.cn.

O175.14

A

1001-9146(2017)04-0094-05