一个微分不等式及在CH方程中的应用

肖 峥，魏 龙

(杭州电子科技大学理学院，浙江 杭州 310018)

一个微分不等式及在CH方程中的应用

肖 峥，魏 龙

(杭州电子科技大学理学院，浙江 杭州 310018)

研究一个一阶微分不等式，探究满足该不等式的函数所具有的性质，并将其应用到Camassa-Holm方程的研究中，给出了Camassa-Holm方程解的爆破条件、解的爆破速率和爆破时间的估计.

微分不等式；Gronwall不等式；CH方程；爆破解

0 引 言

微分不等式在微分方程理论和应用领域中大量出现，是研究微分方程解的存在性、有界性、唯一性、稳定性等性质的重要工具.在最近的研究中，人们发现一个异于Gronwall不等式的一阶二次微分不等式，该不等式在研究微分方程解的性质，特别是研究解的爆破行为时起到十分重要的作用[1-3].本文将探究这个不等式，研究满足不等式的函数所具有的性质，并将这个结果运用到经典的浅水波方程解的性质研究中，给出Camassa-Holm(CH)方程解爆破的初始条件，然后得到解的爆破速率和爆破时间估计.在CH方程爆破解的研究中，本文方法不同于以往文献中的方法，并且得到的解的爆破时间估计是一个新的结果.

1 一阶微分不等式

一些微分不等式在微分方程的研究中占有极其重要的地位，如经典的Gronwall不等式y′≤ay+b,常被用来估计微分方程的解的取值范围[4].本文研究如下一阶微分不等式

y′(t)≤-ay2(t)+b.

(1)

一方面，这个不等式在最近的一些研究中经常出现；另一方面，它也可被看作是将Gronwall不等式的右端关于y的一次函数推广到二次形式的微分不等式.Zhou Y.[1]在2007年最早研究了这个不等式，得到对应的函数在有限时间内爆破并给出爆破时间估计.2016年，Chen R.等[2]提到了这个不等式，但没给出证明.最近，文献[3]研究了这类不等式，但省略了这个不等式的证明过程.文献[3]中的结果推广了文献[1]中的结果，得到更为精确的爆破时间估计.本文探究了满足这个不等式的函数所具有的性质，给出了详细的证明过程，并将其运用到CH方程解的性质研究中，得到一些有趣的结果.下面给出关于微分不等式(1)的结果.

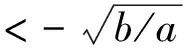
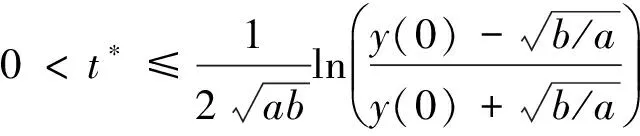
(2)

证明 引理的证明思想类似于文献[3]中的引理12的证明.本文给出证明如下：

首先，假设：当t>0,则y′(t)<0成立.

如果上述结论不成立.由函数y(t)的连续性可知，存在t0∈(0,T),对所有的t∈(0,t0),使得y′(t)<0，且y′(t0)=0成立.因为y(t)在(0,t0)上是单调递减函数，所以有

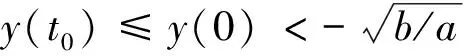
(3)

但由式(1)结合式(3)可知,y′(t0)≤-ay2(t0)+b≤-ay2(0)+b<0.这与y′(t0)=0矛盾.故假设成立.

一方面，对t>0,y′(t)<0，结合式(1)可得

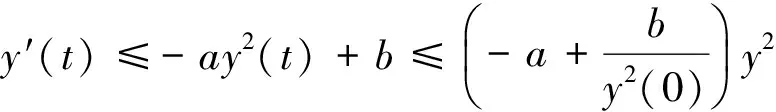
(4)

通过解式(4)，得到

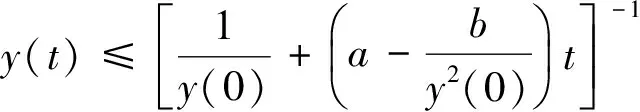
(5)

由这个不等式，不难看出，存在t*>0,使得当t→t*时，y→-∞.

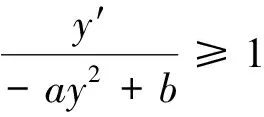
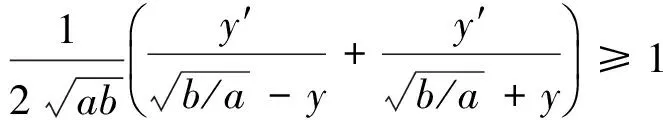
对上述不等式两端同时在(0,t)积分，得

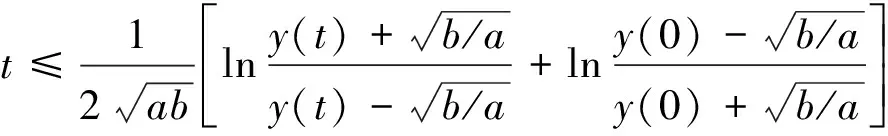
(6)

注意到t→t*时，y(t)→-∞.因此，由式(6)可知式(2)成立.证毕.

2 在CH方程中的应用

考虑经典的浅水波方程——Camassa-Holm方程[5]

(7)

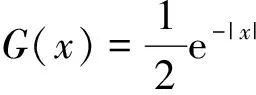
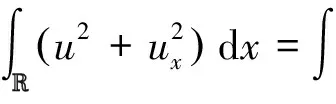
(8)

类似于文献[8]，引入特征方程

(9)

对于CH方程(7)的爆破解，有如下结论.

定理 设u0∈HS(R),s>3/2,T为CH式(7)的解的最大存在时间.如果存在一点x0∈R，当初始值满足

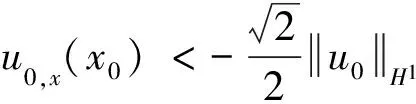
(10)

则方程对应于初始值u0的解u=u(t,x)在有限时间内爆破.即存在T*>0,使得当t→T*时，ux(t,x)→-∞.且T*满足估计

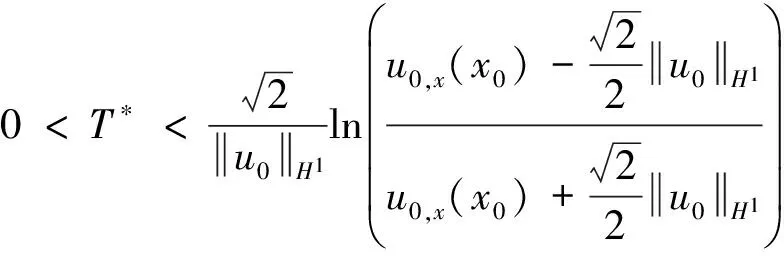
(11)

当t→T*时对应的爆破率为

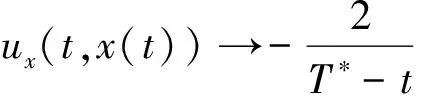
(12)

注 本文式(10)与文献[7]的结果是一致的(见文献[7]中的定理4.2)，但本文的证明方法与文献[7]中不同，且本文给出了相应解的爆破速率和爆破时间估计.

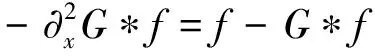
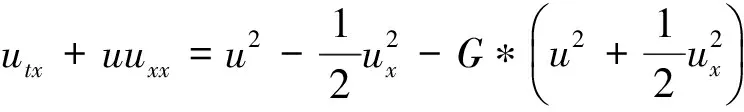
(13)

则由式(13)，得到

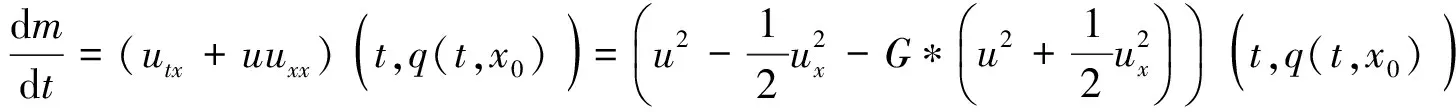
(14)

运用Young不等式，得到估计

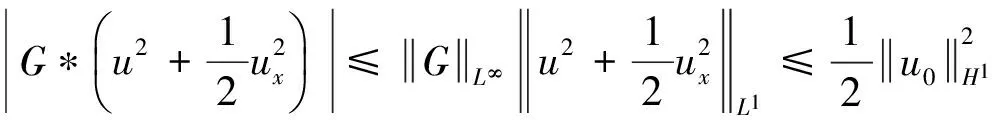
注意到估计式[7]

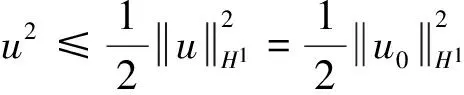
则由式(14)推出

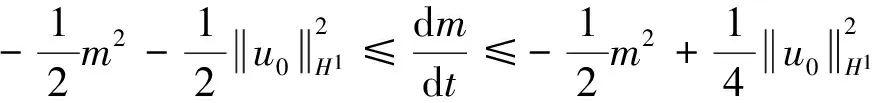
(15)

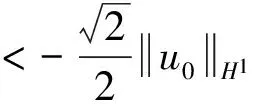
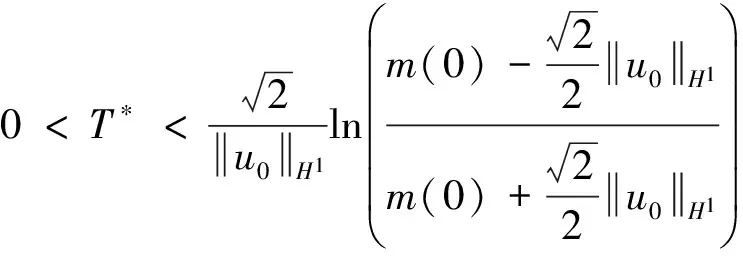
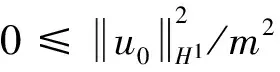
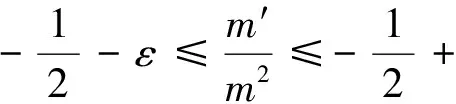
(16)

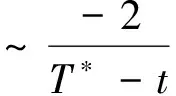
3 结束语

本文研究了满足不等式y′(t)≤-ay2(t)+b的函数所具有的性质，并将其运用到CH方程解的性质研究中，给出了CH方程的解的爆破需要的初始条件、爆破解的爆破时间和爆破速率估计.分析结果表明，微分不等式y′(t)≤-ay2(t)+b具有很好的应用价值和应用前景，可以用来研究更多的微分方程解的性质.

[1]ZHOU Y. Blow-up of solutions to the DGH equation[J]. Journal of Functional Analysis, 2007,250(1):227-248.

[2]CHEN R M, GUO F, LIU Y, et al. Analysis on the blow-up of solutions to a class of integrable peakon equations[J]. Journal of Functional Analysis, 2016,270(6):2343-2374.

[3]WEI L, WANG Y, ZHANG H. Breaking waves and persistence property for a two-component Camassa-Holm system[J]. Journal of Mathematical Analysis and Applications, 2017,445(1):1084-1096.

[4]GRONWALL T H. Note on the derivatives with respect to a parameter of the solutions of a system of differential equations[J]. Annals of Mathematics, 1919,20(2):292-296.

[5]CAMASSA R, HOLM D D. An integrable shallow water equation with peaked solitons[J]. Physical Review Letters, 1993,71(11):1661-1664.

[6]CONSTANTIN A, ESCHER J. Wave breaking for nonlinear nonlocal shallow water equations[J]. Acta Mathematica, 1998,181(2):229-243.

[7]CONSTANTIN A, ESCHER J. Well-posedness, global existence, and blowup phenomena for a periodic quasi-linear hyperbolic equation[J]. Communications on Pure and Applied Mathematics, 1998,51(5):475-504.

[8]CONSTANTIN A. Existence of permanent and breaking waves for a shallow water equation: a geometric approach[J]. Annales-Institut Fourier, 2000,50(2)：321-362.

A First Order Differential Inequality and Its Application to CH Equation

XIAO Zheng, WEI Long

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Differential inequalities are widely applied in the study of differential equations. In this paper, we study a new differential inequality and apply it to the classical Camassa-Holm(CH) equation. We obtain the existence of blow-up solution of the CH equation, and the estimates of blow-up time and blow-up rate are derived.

differential inequality; Gronwall inequality; CH equation; blow-up solution

10.13954/j.cnki.hdu.2017.04.022

2016-10-21

肖峥(1990-),女，江西吉安人，硕士研究生，微分方程.通信作者：魏龙副教授，E-mail:alongwei@163.com.

O175

A

1001-9146(2017)04-0099-04