符号动力系统的拟移位及Smale马蹄模型表示

李二林,陈芳跃,胥海云

(杭州电子科技大学理学院,浙江 杭州 310018)

符号动力系统的拟移位及Smale马蹄模型表示

李二林,陈芳跃,胥海云

(杭州电子科技大学理学院,浙江 杭州 310018)

给出了双边符号序列空间上的一种拟移位映射,通过构造一个同胚映射,证明这种拟移位映射与传统的移位映射拓扑共轭,同时,这个拟移位仍可由Smale马蹄模型来表示.

双边符号空间；Smale马蹄；拟移位映射；Cantor三分集；拓扑共轭

0 引 言

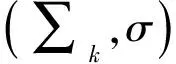
1 符号序列空间的一个拟映射

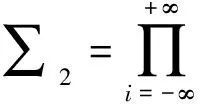
σ(…x-2x-1·x0x1x2…)=(…x-2x-1x0·x1x2…)

(1)

其中xi∈{0,1},i∈Z.现定义一种新的拟移位映射：

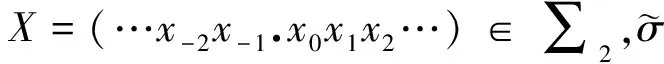
(2)

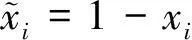
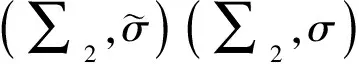
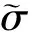
(3)

即ζ(X)的第i个位置的取值为

(4)

其中,“×”为通常的乘法运算.

在∑2上定义距离为

(5)

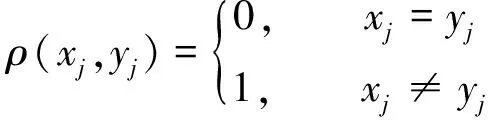
“东方彝风”酒店并不是对纯粹彝族民居的一种简单表现，跟之前所出现过对民居符号进行简单复制的设计理念具有较大的区别。项目设计人员在前期十分细致的研究了地方特色，对彝族传统文化进行了过滤，提取其中的精华，并与现代民居要素之间形成有机融合。从施工技术、材料以及构造等方面进行了全方位分析与研究，使彝族特色与东方元素之间充分结合。

设η∶∑2→∑2为映射：

(6)

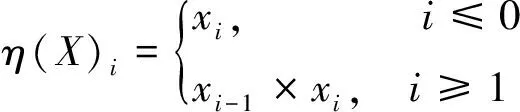
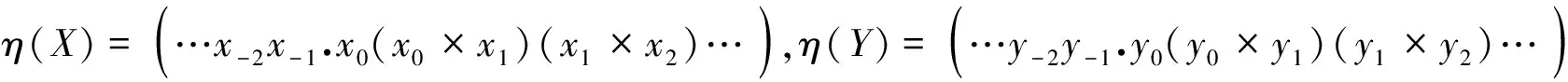
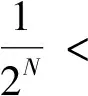
进一步有：

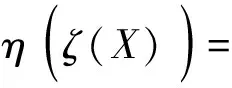
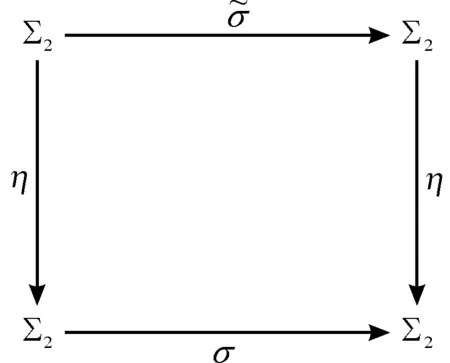
图与σ拓扑共轭交换图

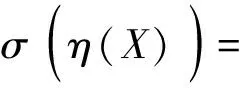
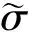
2 拟移位映射的Smale马蹄表示

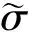
在欧式平面R2中取一个单位正方形M=I×I,定义一个从M到R2的在内同胚映射f∶M→R2如下：先把M沿水平方向线性拉长λ倍,再沿竖直方向压缩λ倍,得到一个λ单位长和1/λ单位宽的长方形,然后把这个长方形中间部分扭转一下,再弯曲成马蹄形状放在M上,几何马蹄变换如图2所示.

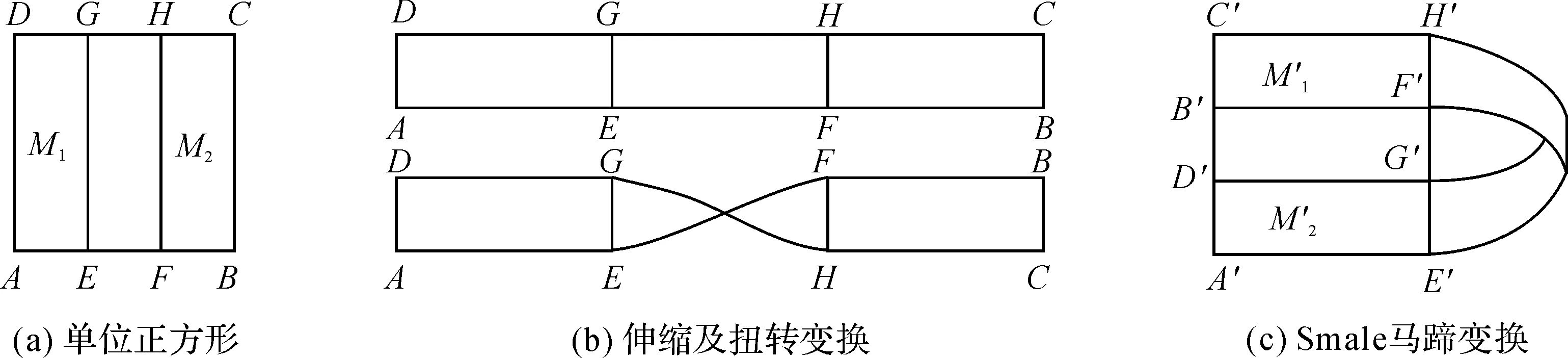
图2 几何马蹄变换图

显然,映射f将M中的长方形M1=ADGE和M2=FHCB分别映射到长方形M1′=A′E′G′D′和M2′=C′H′F′B′,这个映射是局部线性的.当λ=3时,即有

(7)

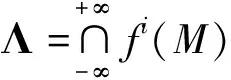
(8)

或

(9)

若x∈C,则x的展开式(8)或式(9)中可以使xi(或x-i)≠1.

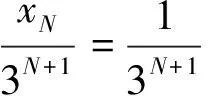
(10)

即(x,y)∈Λ对应一个双向无穷序列,(x,y)～(…x-2x-1·x0x1x2…)xi∈{0,2},i∈Z,这种对应是一一的,称这个对应是Λ的点的符号表示.即h∶Λ→∑2,可以证明h是Λ到∑2的同胚映射.

由式(7)和式(10),对于(x,y)∈Λ,有

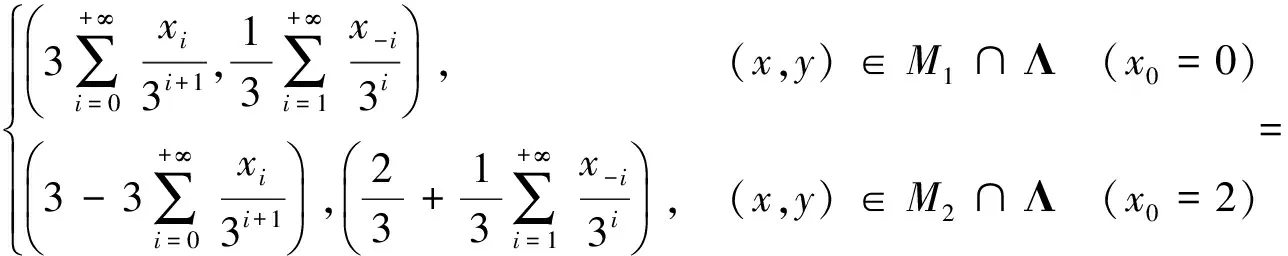
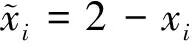
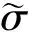
(11)

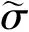
3 结束语

本文定义了一个拟移位映射,并且通过∑2上的一个同胚映射,严格证明了这个拟移位映射与传统的移位映射是拓扑共轭的.有趣的是,这种拟移位可以由Smale马蹄映射的局部线性表示,同时也可以用三进制小数来刻画.本文的思路及方法在部分符号空间的自映射及动力系统的研究中都有一定的参考价值.这种拟移位映射能否刻画其它复杂的映射,有待进一步探讨.

[1]PALIS J, MELO W D. Geometric theory of dynamical systems[M]. New York: Springer-Verlag, 1982:115-181.

[2]THOMPSON J M T, STEWART H B, TURNER R. Nonlinear Dynamics and Chaos[J]. International Journal of Bifurcation & Chaos, 1997,7(4):787-788.

[3]张筑生.微分动力系统原理[M].北京:科学出版社,1987:152-180.

[4]周作领.符号动力系统[M].上海:上海科技教育出版社,1997:71-86.

[5]HIRSCH M W, SMALE S, DEVANEY R L. Discrete Dynamical Systems, Differential Equations, Dynamical Systems, and an Introduction to Chaos[M]. Oxford:Elsevier,2013:329-359.

[6]ARROYO D, ALVAREZ G. Application of Gray codes to the study of the theory of symbolic dynamics of unimodal maps[J]. Communications in Nonlinear Science and Numerical Simulation, 2014,19(7):2345-2353.

[7]BROER H W, TAKENS F. Preliminaries of dynamical systems theory[J]. Handbook of Dynamical Systems, 2010,3:1-42.

[8]樊庆菊.几类系统的混沌性研究[D].武汉:华中科技大学,2010.

[9]CHEN F Y, CHEN F J. Model shift and strange attractor on Möbius strip[J]. Applied Mathematics & Mechanics, 2003,24(7):845-852.

[10]YANG X S, TANG Y. Horseshoes in piecewise continuous maps[J]. Chaos Solitions & Fractals, 2004,19(4):841-845.

[11]麦结华.用5-进制小数描述Smale马蹄映射[J].科学通报,1993,38(21):1932-1935.

Model Shift Mapping of Symbolic Dynamical System and Expression of Smale Horseshoe Model

LI Erlin, CHEN Fangyue, XU Haiyun

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

A kind of model shift map was given in bilateral symbol space. It is proved that the model shift map topological homomorphism the traditional shift map by constructing a homeomorphism map. Besides, the model shift map can be described by Smale horseshoe.

bilateral symbol space; Smale horseshoe; model shift map; Cantor set; topological conjugacy

10.13954/j.cnki.hdu.2017.04.016

2016-10-25

国家自然科学基金资助项目(11171084)

李二林(1991-),男,河南平顶山人,硕士研究生,动力系统与神经网络.通信作者：陈芳跃教授,E-mail：fychen@hdu.edu.cn.

O189

A

1001-9146(2017)04-0075-04