基于时间序列的上证综合指数短期预测分析

刘 亭，赵月旭

(杭州电子科技大学理学院，浙江 杭州 310018)

基于时间序列的上证综合指数短期预测分析

刘 亭，赵月旭

(杭州电子科技大学理学院，浙江 杭州 310018)

对上证日收盘指数2000-12-20至2016-06-20的数据进行建模及预测分析.首先利用相关数据建立ARIMA模型，发现模型的残差存在条件异方差性以及非正态性，于是对残差建立GARCH模型，并对残差的分布类型分别做正态分布、广义误差分布与t分布假设.通过预测精度对比发现，残差服从t分布的ARMA-GARCH模型预测效果更好，预测相对误差仅为1.3%，可为相关投资者提供参考依据.

上证综合指数；ARIMA模型；t-ARMA-GARCH模型；预测

0 引 言

上证综合指数是判断股票价格变化趋势的参考依据，对其进行预测分析，可以帮助投资者及时了解股价未来走势，降低投资风险.2011年，文献[1]对上证指数建立了基于小波的NN-GARCH模型.2014年，文献[2]对上证日收盘指数建立了基于小波分析的ARIMA模型，提高了预测精度.2015年，文献[3]利用基于粒计算的时间序列模型对股票价格进行预测.2016年，文献[4]利用ARMA模型对伦敦股票收益率做了月度和年度预测.本文对上证日收盘指数建立残差服从t分布的t-ARMA(3,3)-GARC H(1,1)模型，对上证日收盘指数进行了预测分析.

1 模型介绍

1.1 ARIMA(p,d,q)模型

ARIMA(p,d,q)模型定义如下[5]：

(1)

1.2ARMA(p,q)-GARCH(m,s)模型

ARMA(p,q)-GARCH(m,s)模型定义如下[6]：

(2)

式中，et～N(0,1)，独立同分布.

1.3 残差分布

对残差的分布类型有以下3种假设[7]：

1)残差εi服从正态分布：εi～N(0,1).

2)残差εi服从t分布：εi～t(λ)，其中t(λ)是均值为0，自由度为λ的t分布.

3)残差εi服从广义误差分布(Generalized Error Distribution，GED)分布.其密度函数为

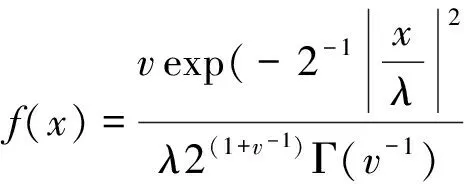
(3)

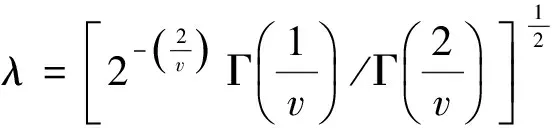
2 实证分析

本文选取上证日收盘指数2000-12-20至2016-06-20的数据进行建模，其中最后5天的收盘指数作为测试数据.

2.1 数据预处理

利用R软件对原始序列进行平稳性分析，时序图如图1所示.

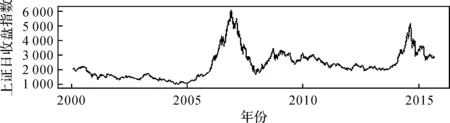
图1 上证指数日收盘指数时序图

从图1可以看出，日收盘指数随时间推移有明显的上升趋势，显然不是一个平稳序列.用单位根检验其平稳性，检验统计量为

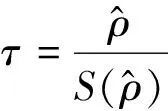
(4)

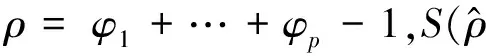
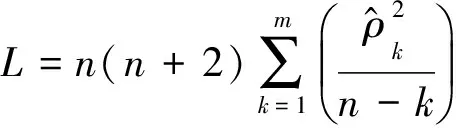
(5)

式中，n为序列观测期数，m为指定延迟期数.检验P值为0.002 61，小于α，认为差分序列非白噪声序列，可以进行建模.

2.2ARIMA(p,d,q)模型的建立

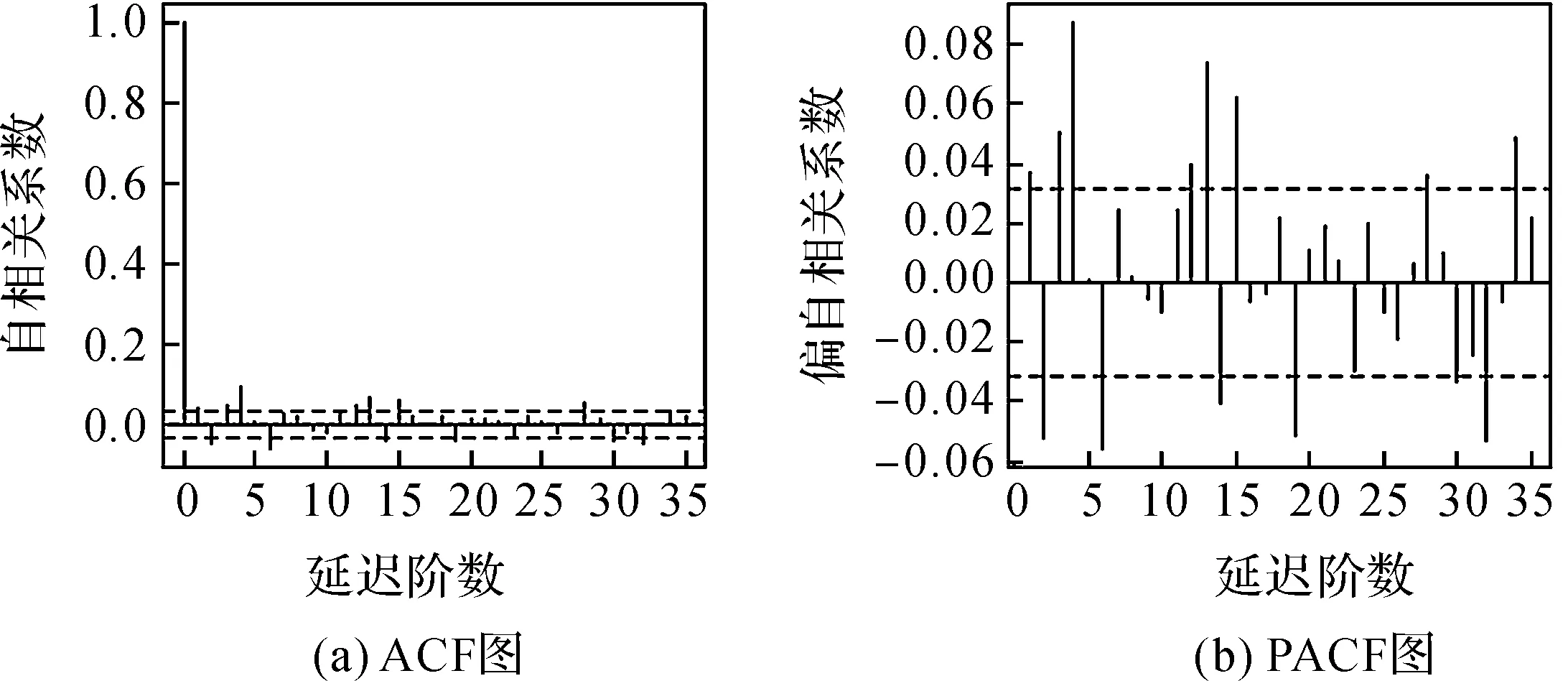
图2 差分序列的ACF，PACF图

利用R软件对原始序列拟合ARIMA模型，通过上面的分析可得这里的差分阶数d=1，对差分序列做自相关系数(ACF)图与偏自相关系数(PACF)图如图2所示.

由图2可以看出，差分序列的ACF，PACF都是拖尾的，需要对原始序列建立ARIMA(p,d,q)模型.通过对比发现，ARIMA(3,1,3)模型更适合对原始序列建模，拟合模型如下：

rt=0.683rt-1-0.769rt-2+0.496rt-3+at-0.646at-1-0.712at-2-0.405at-3.

(6)

式中，rt=xt-xt-1，{xt}为原始序列.

2.3 残差的检验

对残差序列{at}做Box-Ljung检验，检验P值为0.961 62，远大于显著性水平α，接受原假设，认为残差为白噪声序列.残差的Q-Q图与密度图如图3所示.

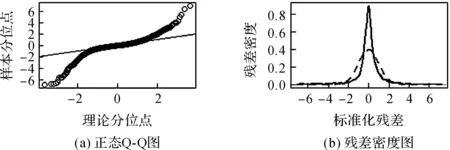
图3 残差的正态性检验

由图3可以看出，残差不服从正态分布，且呈现尖峰后尾现象.

2.4ARCH效应的检验

对残差方差进行ARCH效应检验.ARCH效应的检验原理为对残差方差进行Ljung-Box检验，检验p值为0.000 02远远小于显著性水平α=0.05，认为残差方差存在强相关性，即认为残差序列存在条件异方差性.

2.5ARMA(p,q)-GARCH(m,s)模型的建立

对原始序列分别建立ARIMA(3,1,3)模型以及残差分别服从正态分布、t分布、广义误差分布的ARMA(3,3)-GARCH(1,1)模型，结合AIC信息准则，即AIC值越小，模型的拟合效果越好，选出较优模型.通过对比发现，残差服从t分布的t-ARMA(3,3)-GARCH(1,1)模型为较优模型，拟合模型如下：

(7)

式中，α1+β1<1，且非常接近1，说明过去的波动对未来的波动有正向长期的影响.

2.6ARMA-GARCH模型充分性检验

对模型残差以及残差平方进行白噪声检验，检验p值分别为0.812 81，0.860 51，大于显著性水平α，则认为残差为白噪声序列，不存在异方差性，所建模型合理.

2.7 模型的预测与分析

利用对原始序列建立的ARIMA(3,1,3)模型以及残差分别服从正态分布、t分布、广义误差分布的ARMA(3,3)-GARCH(1,1)模型对测试数据进行预测.预测结果如表1所示.

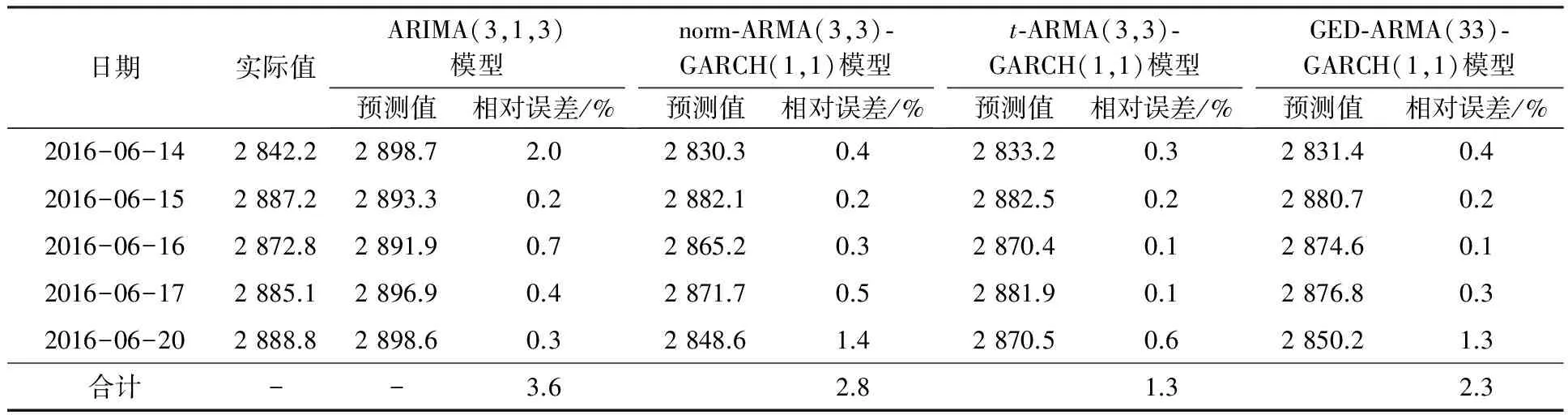
表1 不同模型预测精度对比

表1中，预测结果是通过R软件计算所得，相对误差=|预测值—实际值|/实际值×100%.由表1可以看到，t-ARMA(3,3)-GARCH(1,1)模型预测的相对误差之和仅为1.3%，说明t-ARMA-GARCH模型对上证日收盘指数的条件异方差性和尖峰厚尾现象有更好的刻画，可用于对上证指数未来波动趋势的短期预测.

3 结束语

本文利用t-ARMA-GARCH模型对上证日收盘指数进行了分析，通过预测精度对比发现，残差服从t分布的预测模型能较好地对上证指数进行预测，预测结果可以为相关投资者提供一定的参考依据.下一步研究将ARMA模型与指数GARCH模型、求和GARCH模型等做结合，对上证指数做短期分析，期待预测精度得到进一步提高.

[1]王若星，张德生，彭潇熟.上证指数的基于小波的NN-GARCH模型及实证研究[J].陕西科技大学学报，2011,29(3):142-147.

[2]石鸿雁，尤作军，陈忠菊.基于小波分析的ARIMA模型对上证指数的分析与预测[J].数学的实践与认识，2014,44(23):66-72.

[3]CHEN M Y, CHEN B T. A hybrid fuzzy time series model based on granular computing for stock price forecasting[J]. Information Sciences, 2015,29(4):227-241.

[4]ROUNAGHI M M. Monthly and yearly Forecasting of Time Series in Stock Returns using ARMA model[J]. Physica A: Statistical Mechanics and its Applications, 2016,45(4):10-21.

[5]王燕.应用时间序列分析[M].北京:中国人民大学出版社,2005:146-165.

[6]JONATHAN D. Cryer Kung-Sik Chan.Time Series Analysis with Applications in R[M].北京:机械工业出版社，2011:209-215.

[7]杨琦，曹显兵.基于ARMA-GARCH模型的股票价格分析与预测[J].数学的实践与认识，2016,46(6):21-28.

Short-term Prediction Analysis of Shanghai Composite Index Based on Time Series

LIU Ting, ZHAO Yuexu

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Data of the Shanghai daily closing index between December 20, 2000 and June 20, 2016 is used for modeling and short-term prediction analysis. Firstly, ARIMA model is established. Then, due to the presence of conditional heteroskedasticity and non-normality of the model residuals, ARMA-GARCH model is established. Distribution types of the residuals norm, GED andtare taken into account. By comparison of prediction accuracy, it is found that thet-ARMA-GARCH model has better prediction effect, the relative error of prediction is only 1.3%, which can provide helpful suggestions for relevant investors.

Shanghai composite index; ARIMA model;t-ARMA-GARCH model; prediction

10.13954/j.cnki.hdu.2017.04.015

2016-07-24

国家自然科学基金资助项目(61273093，61473107,U1509205)；浙江省自然科学基金资助项目(LR16F030003)

刘亭(1990-)，女，山东菏泽人，硕士研究生，时间序列分析.通信作者：赵月旭副教授，E-mail：yxzhao@hdu.edu.cn.

F224.7

A

1001-9146(2017)04-0071-04