经典逻辑系统中的随机化再研究*

马巧云，吴洪博

1.西安文理学院 信息工程学院，西安 710065

2.陕西师范大学 数学与信息科学学院，西安 710062

经典逻辑系统中的随机化再研究*

马巧云1+，吴洪博2

1.西安文理学院 信息工程学院，西安 710065

2.陕西师范大学 数学与信息科学学院，西安 710062

给出了经典命题逻辑系统中n元命题公式基于随机数列和随机映射的向量表示形式，利用命题公式的基于随机数列的向量表示形式给出公式的D-随机真度、公式间的D-随机相似度和D-随机伪距离的等价表示形式。说明了一个具体的n元经典命题公式的D-随机真度最多只有22n种情况。利用命题公式间的D-随机相似度和D-随机伪距离的等价表示形式，给出了关于命题公式的D-随机真度、命题公式间的D-随机相似度和D-随机伪距离的一些性质的新的证明。

经典命题逻辑系统；D-随机真度；D-随机相似度；D-随机伪距离

1 引言

为了尝试在人工智能和数值计算之间进行沟通，文献[1-2]从逻辑概念程度化入手，建立了计量逻辑学理论，进而展开了基于逻辑系统中的基本单位——命题公式的程度化的研究和基于这种程度化思想的近似推理的研究[3-7]。但是计量逻辑学存在着缺少随机性这样的不足，文献[8]利用自然数集N上的随机数列而提出了公式的随机真度的概念。这种基于随机性的逻辑概念的程度化方法已经成为当前概率化人工智能研究的一个热点问题[9-15]。文献[15]利用经典命题逻辑中公式的赋值及赋值顺序给出了公式的向量表示形式，利用向量表示形式给出公式的真度和公式间伪距离的定义，使得经典命题逻辑中公式的伪距离的讨论得到简化。

本文给出了经典命题逻辑系统中公式基于随机数列D的向量表示形式，利用公式的向量表示形式给出公式的D-随机真度、公式间的D-随机相似度和D-随机伪距离的等价表示形式。利用随机相似度和随机伪距离的等价表示形式，给出了关于随机相似度和随机伪距离的一些性质的新的证明。这些研究为深入了解逻辑空间的性质做了准备，也为后续的研究提供了一些方法和借鉴。

2 预备知识

定义1[1]设S={p1,p2,…}是可数集，¬是一元运算，∨、→是二元运算，由S生成的(¬,∨,→)型自由代数记作F(S)。F(S)中的元称作合式公式，简称公式。S中的元称作原子公式或原子命题。

定义2[1]设{0,1}为最简布尔代数，其中¬x=1-x，x→y=0当且仅当x=1,y=0。称(¬,→)型同态v:F(S)→{0,1}(v(¬A)=¬v(A),v(A→B)=v(A)→v(B))为 F(S)在{0,1}中的赋值，简称v为赋值。F(S)的全体赋值之集记为Ω。

定义3[8]设D=(P1,P2,…)是(0,1)中的随机数列，∀α=(x1,x2,…,xn)∈{0,1}n，

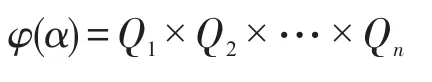
这里，当xk=1时Qk=Pk；当xk=0时Qk=1-Pk(k=1,2,…,n)。则得一映射

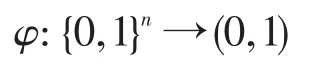
称φ为{0,1}n上的D-随机化映射。

定义 4[8]设A=A(q1,q2,…,qn)∈F(S)，令 [A]=(1)，μ([A])=∑{φ(α):α∈(1)}，τD(A)=μ([A])，称 τD(A)为A的D-随机真度。

3 基于经典逻辑公式的向量表示的D-随机真度

文献[15]已说明总可以假定命题公式A、B含有相同多的原子公式。

设fA(x1,x2,…,xn):{0,1}n→{0,1}是由公式A诱导的Boole函数（其中fA(x1,x2,…,xn)中x1,x2,…,xn的连接方式与A(q1,q2,…,qn)中q1,q2,…,qn的连接方式完全相同）。令Σ={0,1}n,设∀A(q1,q2,…,qn)∈F(S),B(q1,q2,…,qn)∈F(S),∀α∈Σ，一定有：

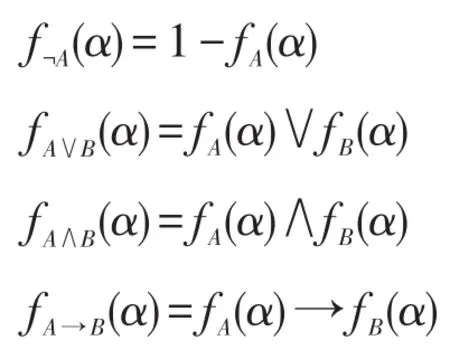
将Σ中的2n个元按照字典顺序依次记作α1,α2,…,α2n。对于具体的n元公式A(q1,q2,…,qn)，使fA(x1,x2,…,xn)=1的α是确定的，不妨依次记作αi1,αi2,…,αik，其 中i1,i2,…,ik∈{1,2,…,2n}，令Σ1={αi1,αi2,…,αik}。同样，使fA(x1,x2,…,xn)=0 的 α 也是确定的，依次记作 αj1,αj2,…,αjl，其中j1,j2,…,jl∈{1,2,…,2n}，令Σ0={αj1,αj2,…,αjl}。显然，k+l=2n。

定义5设D=(P1,P2,…)是(0,1)中的随机数列，φ为{0,1}n到{0,1}的D-随机化映射，令

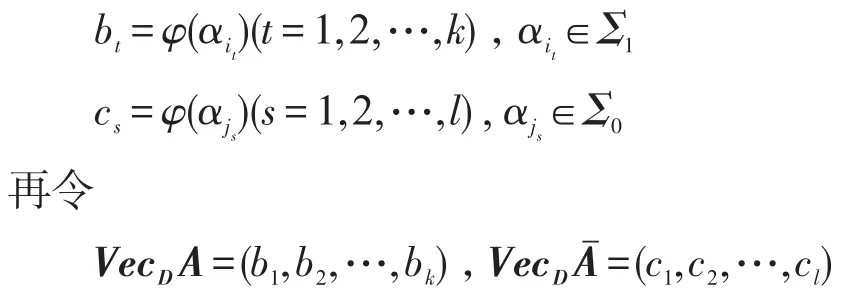
称VecDA、VecD分别为公式A基于随机数列D的1-值向量和0-值向量。

定义 6设A(q1,q2,…,qn)∈F(S)，VecDA=(b1,b2,…,bk)，VecD=(c1,c2,…,cl)分别为公式A基于随机数列D的1-值向量和0-值向量，令

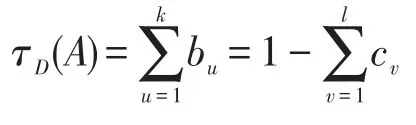
称τD(A)为A的D-随机真度。

显然，定义6与文献[8]中的D-随机真度的定义是一致的。并且当k＞l时，用第二个式子计算是比较容易的。

命题1设A(q1,q2,…,qn)∈F(S)，VecDA=(b1,b2,…,bk)，VecD=(c1,c2,…,cl)分别为公式A基于随机数列D的1-值向量和0-值向量，则：

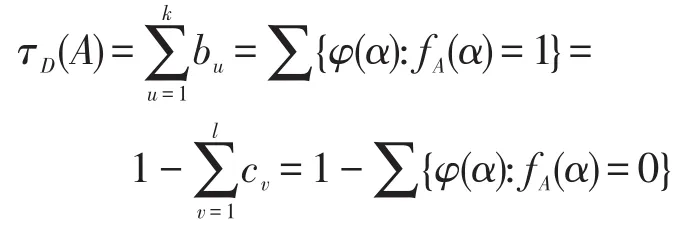
证明由定义6可直接得到。

命题2设A(q1,q2,…,qn)∈F(S)，D=(P1,P2,…)是(0,1)中的随机数列，则：

证明（1）、（2）、（3）可由定义直接得到。证明略。

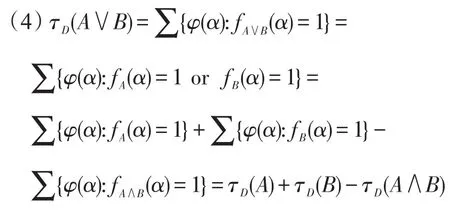
命题 3设A(q1,q2,…,qn),B(q1,q2,…,qn)，C(q1,q2,…,qn)∈F(S),D=(P1,P2,…)是(0,1)中的随机数列，α,β∈[0,1]。

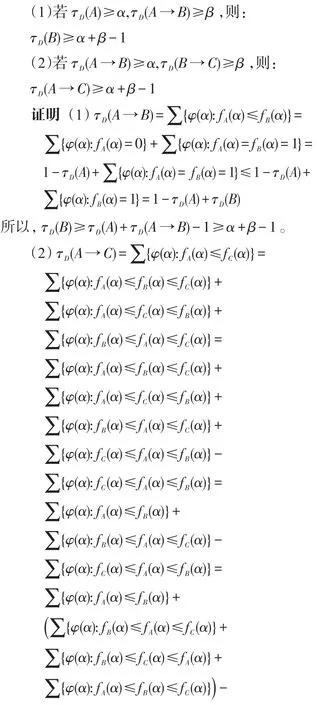
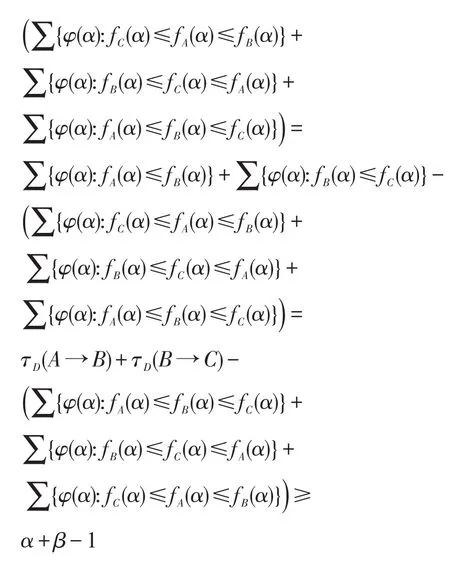
命题4设D=(P1,P2,…)是(0,1)中的随机数列。对于n元命题公式集Fn={A(q1,q2,…,qn):A∈F(S)}中的公式A来说，A的D-随机真度最多只有22n种。

证明设A(q1,q2,…,qn)∈Fn，fA(x1,x2,…,xn)∈F(S)是公式A对应的n元Boole函数。

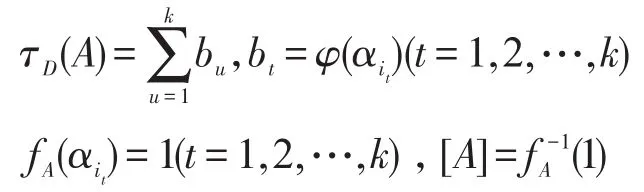
若[A]=Φ，τD(A)只有=1种情况；

若[A]={αi}，τD(A)最多有种情况；

若[A]={αi,αj}，τD(A)最多有种情况；

…

若 [A]={α1,α2,…,α2n}，τD(A)最多有种情况。

综上可知，n元命题公式A的D-真度τD(A)最多只有种不同的情况。

4 公式的相似度和公式间的伪距离

定义7[8]设D=(P1,P2,…)是(0,1)中的随机数列，A,B∈F(S)，令

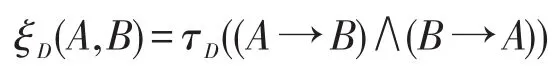
称ξD(A,B)为公式A与B的D-相似度。

命题5设A,B∈Fn，fA(x1,x2,…,xn)∈F(S),fB(x1,x2,…,xn)∈F(S)分别是公式A、B对应的n元Boole函数，则：

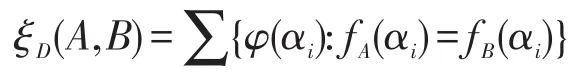
证明因为 ξD(A,B)=τD((A→B)∧(B→A))=∑{φ(α):f(A→B)∧(B→A)(α)=1}，而

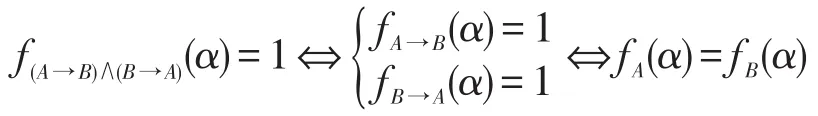
所以 ξD(A,B)=∑{φ(αi):fA(αi)=fB(αi)}。

命题6[8]设D=(P1,P2,…)是(0,1)中的随机数列，A,B,C∈F(S)，则：

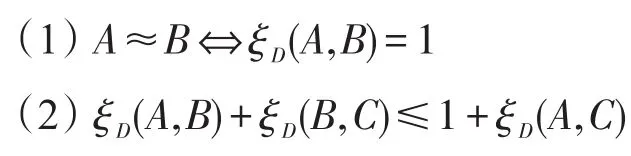
根据命题5给出命题6不同于文献[8]的证明。

证明（1）设fA(x1,x2,…,xn)，fB(x1,x2,…,xn)分别是公式A、B对应的n元Boole函数，A≈B当且仅当∀α∈Σ,fA(α)=fB(α)，当且仅当 ξD(A,B)=∑{φ(αi):fA(αi)=fB(αi)}=1。

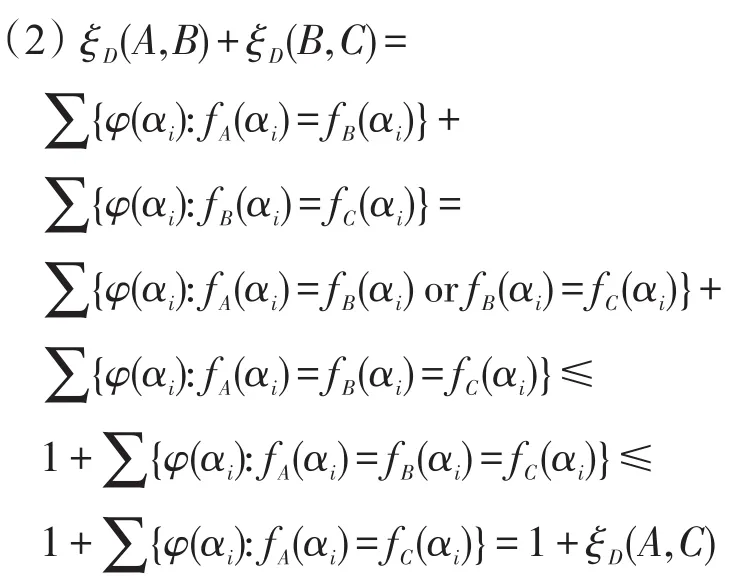
定义8[8]设D=(P1,P2,…)是(0,1)中的随机数列，A,B∈F(S)，令

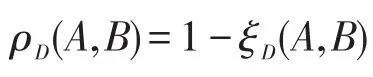
称 ρD(A,B)是F(S)上的伪距离，称为公式A与B的D-逻辑伪距离，称(F(S),ρD)为D-逻辑度量空间。

命题7设A,B∈Fn,fA(x1,x2,…,xn)∈F(S),fB(x1,x2,…,xn)∈F(S)分别是公式A、B对应的n元Boole函数，则：

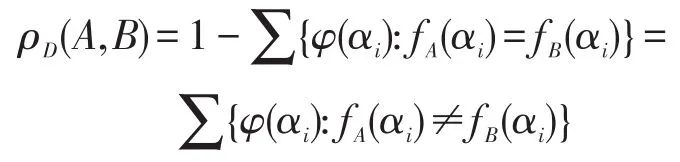
证明因为 ρD(A,B)=1-ξD(A,B)=1-∑{φ(αi):fA(αi)=fB(αi)}，而∑{φ(αi)=1:αi∈Σ},则：

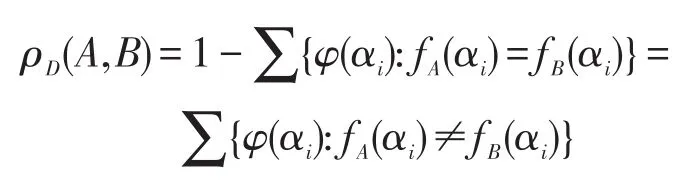
命题8在伪距离空间(F(S),ρD)中，以下结论成立：

证明略。

命题9设A(q1,q2,…,qn),B(q1,q2,…,qn),C(q1,q2,…,qn)∈F(S)，D=(P1,P2,…)是(0,1)中的随机数列，则：

ρD(A→C,B→D)≤ρD(A,B)+ρD(C,D)

证明因为 ρD(A,B)=1-ξD(A,B)，所以只需证

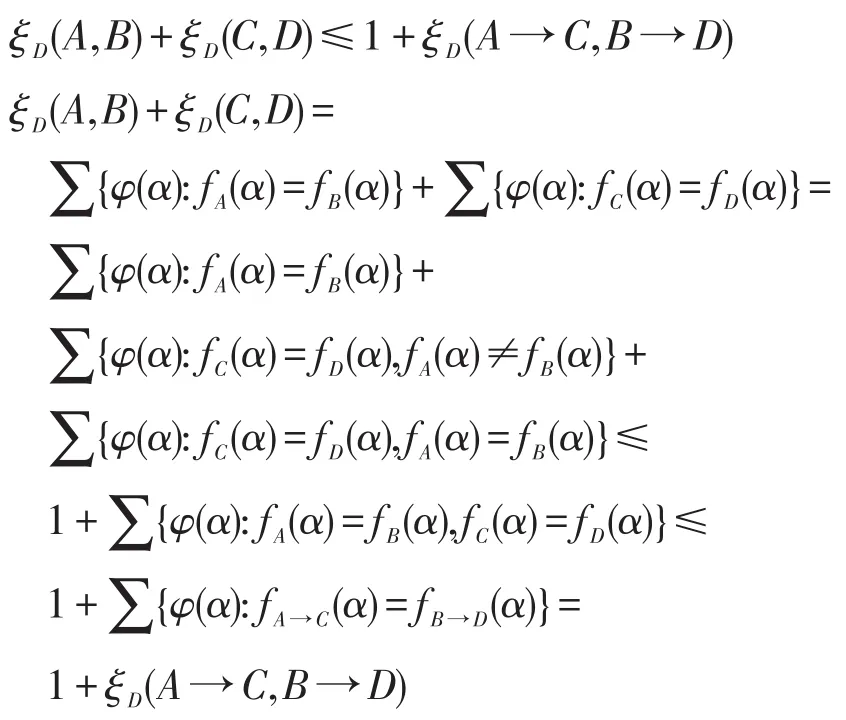
由命题9，可以证明逻辑连接词→在(F(S),ρD)中连续[8]。

命题10在伪距离空间(F(S),ρD)中，以下结论成立：

5 结束语

本文利用经典命题逻辑中公式的赋值及赋值顺序给出了公式的基于随机数列D的向量表示形式，利用命题公式的向量表示形式给出公式的D-随机真度的等价定义；同时给出了基于随机数列D-公式间的D-随机相似度和D-随机伪距离的等价定义，证明了这种定义与文献[8]中的定义等价。说明了一个具体的n元经典命题公式的D-随机真度最多只有22n种情况。本文还得到了公式间的D-随机真度、D-随机相似度和D-随机伪距离的一些简单性质，根据这些性质，可以证明在随机伪距离空间(F(S),ρD)中，逻辑连接词都是连续的。因为这种定义与文献[8]中的定义等价，所以在经典命题逻辑中利用随机伪距离进行近似推理的研究与文献[8]的结论是一致的，在此不用列出。关于在多值命题逻辑系统中是否存在与本文类似的随机真度和随机伪距离的定义，将另文进行讨论。

References:

[1]Wang Guojun.Introduction to mathematical logic and resolution principle[M].2nd ed.Beijing:Science in China Press,2006.

[2]Wang Guojun.Quantitative logic(I)[J].Chinese Journal of Engineering Mathematics,2006,23(2):191-215.

[3]Wang Guojun,Song Jianshe.Graded method in propositional logic[J].Acta Electronic Sinica,2006,34(2):252-257.

[4]Cui Meihua.The integral truth degree and pseudo-distance of formulas in the fuzzy logic system[J].Chinese Journal of Engineering Mathematics,2010,27(5):873-882.

[5]Li Bijing,Wang Guojun.Logic pseudo-metric spaces of regular implication operators[J].Acta Electronic Sinica,2010,38(3):497-502.

[6]Han Banghe,Li Yongming.Approximate reasoning in quantitative logic[J].Fuzzy Systems and Mathematics,2010,24(5):1-7.

[7]Zhou Jianren,Wu Hongbo.An equivalent definition and some properties of truth degrees in Lukasiewicz proposition logic system[J].Chinese Journal of Engineering Mathematics,2013,30(4):580-590.

[8]Hui Xiaojing,Wang Guojun.Randomization of classical inference patterns and its application[J].Science in China:Series E,2007,37(6):801-812.

[9]Hui Xiaojing,Wang Guojun.Randomization of classical inference patterns and its application(Ⅱ)[J].Fuzzy systems and Mathematics,2008,22(3):21-26.

[10]Cui Meihua.The D-conditional truth degree of formulas and approximate reasoning in theG3propositional logic system[J].Journal of Shandong University:Natural Science Edition,2010,45(11):52-58.

[11]Hui Xiaojing,Chang Jian.Some remarks on the randomized truth degree[J].Fuzzy Systems and Mathematics,2009,23(6):38-43.

[12]Lou Yan,Feng Feiyan,Zuo Weibing.Conditional randomized truth degree of formulas in Lukasiewicz n-valued propositional logic[J].Computer Engineering and Applications,2012,48(33):63-67.

[13]Zuo Weibing.The conditional randomized truth degree of formulas in the fuzzy logic systemL∗[J].Journal of Shandong University:Natural Science Edition,2012,47(6):121-126.

[14]Hui Xiaojing.Randomization ofR03-valued propositional logic system[J].Acta Mathematicae Applicate Sinica,2009,32(1):19-27.

[15]Ma Qiaoyun,Wu Hongbo.An equivalent definition about truth degree of formula and pseudo-metric among formulas in classical logic system[J].Fuzzy Systems and Mathematics,2013,27(1):28-33.

附中文参考文献：

[1]王国俊.数理逻辑引论与归结原理[M].2版.北京:科学出版社,2006.

[2]王国俊.计量逻辑学(Ⅰ)[J].工程数学学报,2006,23(2):191-215.

[3]王国俊,宋建社.命题逻辑中的程度化方法[J].电子学报,2006,34(2):252-257.

[4]崔美华.模糊逻辑系统中公式的积分真度和伪距离[J].工程数学学报,2010,27(5):873-882.

[5]李璧镜,王国俊.正则蕴含算子所对应的逻辑伪度量空间[J].电子学报,2010,38(3):497-502.

[6]韩邦合,李永明.计量逻辑学中的近似推理[J].模糊系统与数学,2010,24(5):1-7.

[7]周建仁,吴洪博.Łukasiewicz命题逻辑系统中真度的等价定义及其相关性质[J].工程数学学报,2013,30(4):580-590.

[8]惠小静,王国俊.经典推理模式的随机化研究及其应用[J].中国科学:E辑,2007,37(6):801-812.

[9]惠晓静,王国俊.经典推理模式的随机化研究及其应用(II)[J].模糊系统与数学,2008,22(3):21-26.

[10]崔美华.逻辑系统G3中命题的D-条件真度与近似推理[J].山东大学学报:理学版,2010,45(11):52-58.

[11]惠晓静,常健.关于随机真度的若干注记[J].模糊系统与数学,2009,23(6):38-43.

[12]娄妍,冯飞䶮,左卫兵.Lukasiewiczn值命题逻辑中公式的条件随机真度[J].计算机工程与应用,2012,48(33):63-67.

[13]左卫兵.模糊命题逻辑L∗中公式的条件随机真度[J].山东大学学报:理学版,2012,47(6):121-126.

[14]惠小静.三值R0命题逻辑系统的随机化[J].应用数学学报,2009,32(1):19-27.

[15]马巧云,吴洪博.经典逻辑系统中公式的真度及公式间伪距离的一种等价定义[J].模糊系统与数学,2013,27(1):28-33.

WU Hongbo was born in 1959.He received the Ph.D.degree from Sichuan University in 2001.Now he is a professor and Ph.D.supervisor at Shaanxi Normal University.His research interests include topology on lattice and nonclassical logic.吴洪博（1959—），男，陕西咸阳人，2001年于四川大学获得理学博士学位，现为陕西师范大学数学与信息科学学院教授、博士生导师，主要研究领域为格上拓扑学，非经典数理逻辑。

CNKI推出《中国高被引图书年报》

日前，中国知网（CNKI）中国科学文献计量评价研究中心推出了一套《中国高被引图书年报》，该报告基于中国大陆建国以来出版的422万余本图书被近3年国内期刊、博硕、会议论文的引用频次，分学科、分时段遴选高被引优秀学术图书予以发布。据研制方介绍，他们统计并分析了2013—2015年中国学术期刊813万余篇、中国博硕士学位论文101万余篇、中国重要会议论文39万余篇，累计引文达1 451万条。根据统计数据，422万本图书至少被引1次的图书达72万本。研制方根据中国图书馆分类法，将72万本图书划分为105个学科，分1949—2009年和2010—2014年两个时间段，分别遴选被引最高的TOP10％图书，共计选出70 911本优秀图书收入《中国高被引图书年报》。统计数据显示，这7万本高被引优秀图书虽然只占全部图书的1.68％，却获得

67.4％的总被引频次，可见这些图书质量上乘，在同类图书中发挥了更加重要的作用。该报告还首次发布各学科“学科h指数”排名前20的出版单位的评价指标，对客观评价出版社的社会效益——特别是学术出版物的社会效益具有重要的参考价值。

该报告从图书被引用的角度出发，评价图书的学术影响力，弥补了以销量和借阅等指标无法准确评价学术图书的缺憾，科学、客观地评价了图书、图书作者以及出版单位对各学科发展的贡献。

《中国高被引图书年报》把建国以来出版图书全部纳入评价范围属国内首创，是全面、客观评价图书学术影响力的工具，填补了目前图书学术水平定量评价的空白，在帮助图书馆建设特色馆藏和提高服务水平、帮助出版管理部门了解我国学术出版物现状、帮助科研机构科研管理、帮助读者购买和阅读图书等方面，均具有较强的参考价值，也为出版社评估出版业绩、决策再版图书、策划学科选题提供有用的信息。

《中国高被引图书年报》由《中国学术期刊（光盘版）》电子杂志社有限公司出版。该产品的形式为光盘电子出版物，分为理学、工学、农学、医学、人文科学和社会科学6个分卷，随盘赠送图书，欢迎您咨询、订购。

咨询电话：010-82710850,82895056转8599;E-mail：aspt@cnki.net

Restudy on Randomization of Classical Logic System*

MAQiaoyun1+,WU Hongbo2
1.College of Information Engineering,Xi’an University,Xi’an 710065,China
2.College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China
+Corresponding author:E-mail:231687227@qq.com

MA Qiaoyun,WU Hongbo.Restudy on randomization of classical logic system.Journal of Frontiers of Computer Science and Technology,2017,11(8)：1354-1360.

This paper gives the vector representation of n-ary formula in classical propositional logic system based on random sequence and random mapping,defines the D-randomized truth degree of formulas and D-randomized similarity degree and D-randomized pseudo-metric among formulas based on the vector representation of formula,and explains that the definitions of truth degree and D-randomized pseudo-metric are equivalent to the original probability definition.Then,this paper proves that the D-randomized truth degree of n-ary formula is not more than22ncases.Finally,some simple properties of pseudo-metric among formulas are obtained based on the equivalent representation of D-randomized similarity degree and D-randomized pseudo-metric among formulas.

classical propositional logic system;D-randomized truth degree;D-randomized similarity degree;D-randomized pseudo-metric

n was born in 1973.She

the M.S.degree in mathematics from Shaanxi Normal University in 2007.Now she is an associate professor at Xi’an University.Her research interest is non-classical logic. 马巧云（1973—），女，陕西咸阳人，2007年于陕西师范大学获得硕士学位，现为西安文理学院副教授，主要研究领域为非经典逻辑。

A

：O141

*The National Natural Science Foundation of China under Grant No.61572016(国家自然科学基金);the Science and Technology Planning Project of Xi'an under Grant No.2016CXYWL23(西安科技计划项目).

Received 2017-01,Accepted 2017-04.

CNKI网络优先出版:2017-04-13,http://kns.cnki.net/kcms/detail/11.5602.TP.20170413.1027.002.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology 1673-9418/2017/11(08)-1354-07

10.3778/j.issn.1673-9418.1701001

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056