近似空间复合的矩阵表示*

姚爱梦，米据生

河北师范大学 数学与信息科学学院，石家庄 050024

近似空间复合的矩阵表示*

姚爱梦+，米据生

河北师范大学 数学与信息科学学院，石家庄 050024

近似空间；复合；粗糙集；模糊集；矩阵

1 引言

20世纪80年代初Pawlak提出的粗糙集理论[1]是一种处理不精确、不确定、不完全数据的新型数学理论，已在生活中的众多领域被广泛应用。粗糙集理论的核心是利用等价关系从近似空间中导出一对上、下近似算子。然而在一些实际问题中等价关系往往不容易被满足，涉及的论域也可能不止一个[2]，因而扩充原有的粗糙集模型和改进计算方法是粗糙集理论中一个重要的研究内容。

矩阵是一种高效的并且可计量化的工具。在粗糙集理论中，早期Guan等人[3]提出了信息系统的矩阵算法，他将信息系统中的等价关系用矩阵的形式进行了重新描述，但在这个过程中矩阵更多的只是一种表示形式，而不能用来参与具体计算。之后刘贵龙[4-6]利用集合的特征函数，提出了一种基于矩阵布尔运算的求解上、下近似的方法。近几年来，很多学者[2,7-10]致力于研究如何利用矩阵刻画粗糙集的上、下近似，其中刘财辉在文献[11]中提出了一种基于一般二元关系的粗糙集上、下近似的直接矩阵求法。本文主要研究两个近似空间的复合问题，并考察如何将经典集和模糊集的上、下近似用矩阵表示和求解的问题。总的来说，矩阵方法使人们从另一视角对粗糙集的认识更加深刻，也使得计算大大简化。

2 预备知识

下面主要介绍广义近似空间和广义模糊近似空间中的一些基础知识。

定义1[12]设U和V是两个非空有限集合，称为论域。任何子集R⊆U×V都称为从U到V的二元关系。如果U=V，则称R是U上的二元关系。

定义2[12]称三元组(U,V,R)为广义近似空间，其中U和V是两个非空的有限论域，R是从U到V的二元关系。

定义3[12]设(U,V,R)为广义近似空间，分别定义两个算子Rs:U→P(V)及Rp:V→P(U)：

例1在广义近似空间(U,V,R)中，论域U={x1,x2,x3,x4,x5,x6}论域V={y1,y2,y3,y4,y5,y6,y7}。U和V的二元关系如表1。

故易知：Rs(x1)={y1,y4},Rs(x2)={y1,y2,y3,y4},Rs(x3)={y1,y4,y5,y6,y7} ,Rs(x4)={y1,y2,y3,y4},Rs(x5)={y5,y6,y7},Rs(x6)={y5,y6,y7};Rp(y1)={x1,x2,x3,x4},Rp(y2)={x2,x4},Rp(y3)={x2,x4},Rp(y4)={x1,x2,x3,x4},Rp(y5)={x3,x5,x6},Rp(y6)={x3,x5,x6},Rp(y7)={x3,x5,x6}。

若X={x1,x2,x3,x4},则(X)={y1,y2,y3,y4},(X)={y1,y2,y3,y4,y5,y6,y7};

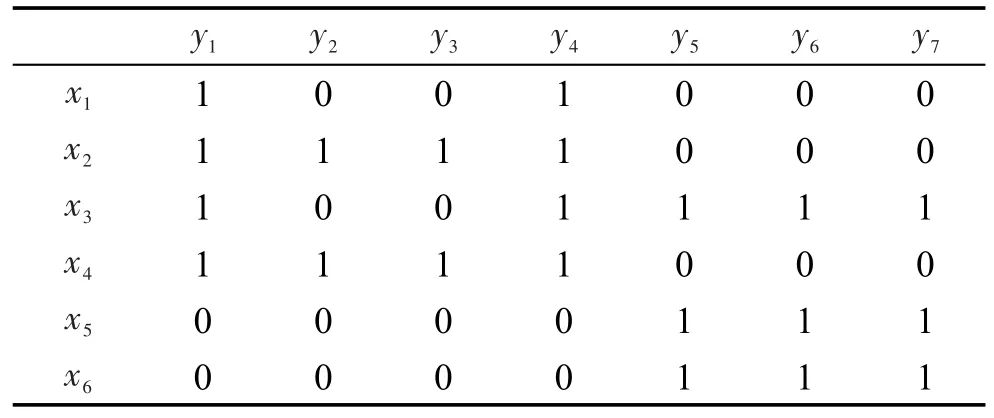
Table1 Binary relation of U and V表1 U和V的二元关系表

若Y={y1,y2,y3,y4},则(Y)={x1,x2,x4},(Y)={x1,x2,x3,x4}。

定义4[13]设U和V是非空有限论域，U的模糊子集全体记为F(U)。映射R:U×V→[0,1]，称为从U到V的模糊二元关系。∀A,B∈F(U)有：(A⋃B)(x)=∨(A(x),B(x));(A⋂B)(x)=∧{A(x),B(x)}。模糊集A的α截集Aα为Aα={x|A(x)≥α}，α∈[0,1]。容易验证：A(x)=sup{α:x∈Aα}，简记为

定义5[14]称三元组(U,V,R)为广义模糊近似空间，如果U和V为非空有限论域，R是从U到V的模糊二元关系。

定义6[15]设(U,V,R)为广义模糊近似空间，∀A∈F(U),B∈F(V)，定义A和B的下近似和上近似分别为：

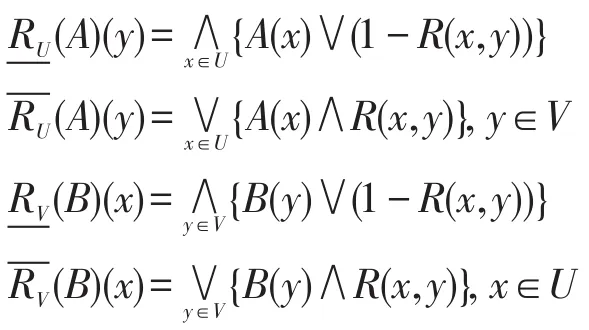
引理1[15]设(U,V,R)为广义模糊近似空间，∀A∈F(U)，B∈F(V)，有：

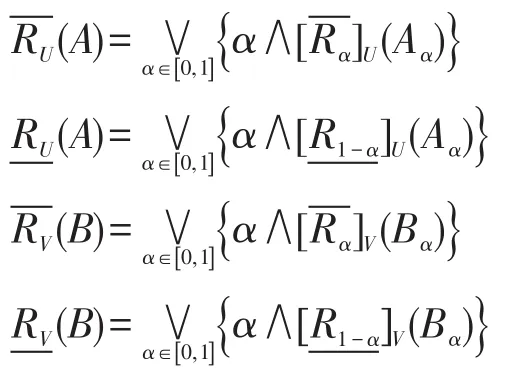
例2在广义模糊近似空间(U,V,R)中，论域U={x1,x2,x3}，论域V={y1,y2,y3,y4},U和V的模糊二元关系如表2。

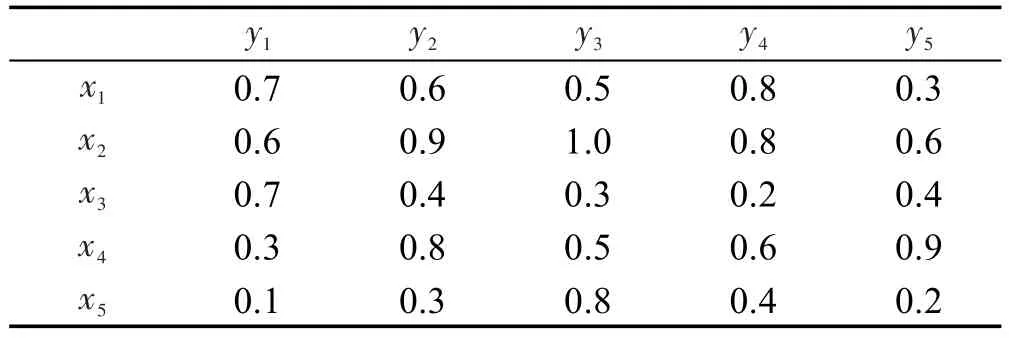
Table2 Fuzzy binary relation of U and V表2 U和V的模糊二元关系表

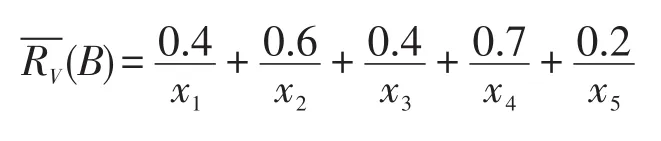
3 近似空间的复合

下面主要介绍广义近似空间复合和广义模糊近似空间复合的相关知识，并对复合近似空间中的算子和原来近似空间中的算子之间的关系作进一步研究。

定义7[16]设A=(U,V,R)和B=(V,W,S)是两个广义近似空间，A与B的复合定义为广义近似空间A⊗B=(U,W,T)，其中T是二元关系R和S的复合，即T=R∘S，其中运算∘为二元关系的复合。

性质1设A=(U,V,R)和B=(V,W,T)是两个广义近似空间，A⊗B=(U,W,T)是A与B合成的广义近似空间，则∀x∈U和∀z∈W，(x,z)∈T⇔Rs(x)⋂Sp(z)≠∅。

证明T=R∘S，由关系复合的定义知∀x∈U和∀z∈W，(x,z)∈T 当且仅当∃y∈V 使得(x,y)∈R,(y,z)∈S，即∃y∈V 使得y∈Rs(x)且y∈Sp(z)，即Rs(x)⋂Sp(z)≠∅。

性质2[16]设A=(U,V,R)和B=(V,W,T)是两个广义近似空间，A⊗B=(U,W,T)是A与B复合的广义近似空间，则：

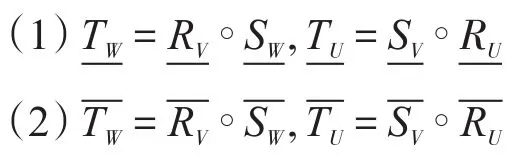
其中运算∘为算子的复合。

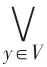
性质3[16]设A=(U,V,R)和B=(V,W,T)是两个广义模糊近似空间，A⊗B=(U,W,T)是A与B复合的广义模糊近似空间，则：

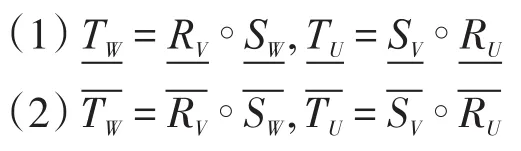
其中运算∘为算子的复合。

性质4设A=(U,V,R)和B=(V,W,T)是两个广义模糊近似空间，A⊗B=(U,W,T)是A与B复合的广义模糊近似空间，则∀α∈[0,1]，Tα=Rα∘Sα，其中运算∘为二元关系的复合。

另一方面，∀(x,z)∈Rα∘Sα，∃y1∈V 使(x,y1)∈Rα且(y1,z)∈Sα，故R(x,y1)≥α 且 S(y1,z)≥α。下证T(x,z)={R(x,y)∧S(y,z)}≥α。显然y1∈V 满足{R(x,y1)∧S(y1,z)}≥α，从而对y1∈V有{R(x,y1)∧S(y1,z)}≥α，又因为T(x,z)≥{R(x,y1)∧S(y1,z)}，故 T(x,z)≥α，所以(x,z)∈Tα，即Rα∘Sα⊆Tα。

这样便证明了Tα=Rα∘Sα。

性质5设A=(U,V,R)和B=(V,W,T)是两个广义模糊近似空间，A⊗B=(U,W,T)是A与B复合的广义模糊近似空间，则∀X⊆U,Y⊆V有：

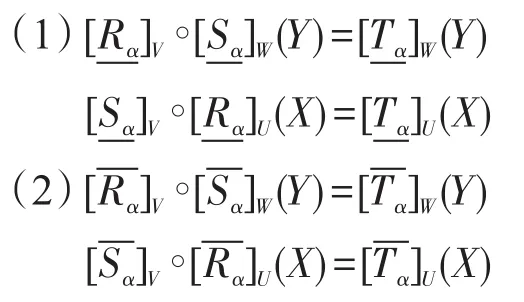
证明根据性质2可证。

性质6设A=(U,V,R)和B=(V,W,T)是两个广义模糊近似空间，A⊗B=(U,W,T)是A与B复合的广义模糊近似空间，则∀A∈F(U)，B∈F(V)有：

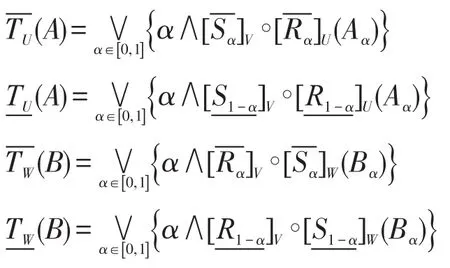
证明由引理1和性质5可证。

4 近似空间复合的矩阵表示

下面主要定义几种矩阵运算，进而根据矩阵运算将复合后的近似空间中的一些运算用矩阵进行表示和求解。

定义9设A=(aik)n×m，B=(bkj)m×l是两个矩阵，定义矩阵 C=A∘B=(cij)n×l，D=A∗B=(dij)n×l，F=A·B，如下：

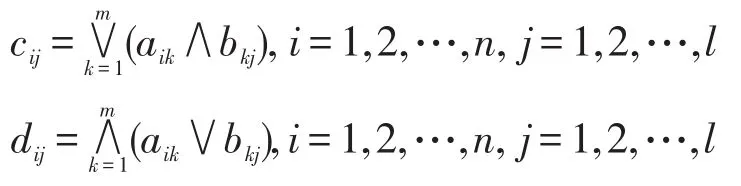
A·B表示普通意义下的矩阵乘法。

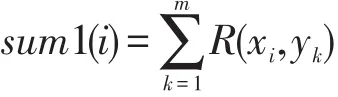
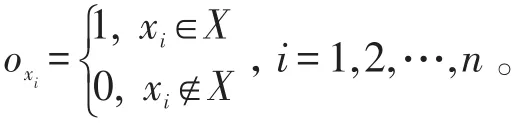
性质7设(U,V,R)为广义近似空间，U={x1,x2,…,xn},V={y1,y2,…,ym},关系矩阵为A=(R(xi,yk))n×m,∀X⊆U,Y⊆V，令 M1=A·OY=(m11,m12,…,m1n)T，M2=AT·OX=(m21,m22,…,m2m)T,则X和Y的上、下近似分别为：

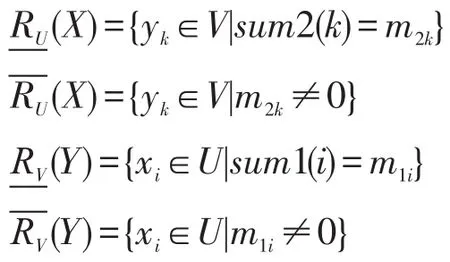
证明首先证明(Y)={xi∈U|sum1(i)=m1i},(Y)={xi∈U|m1i≠0}。

例3续例1，由上述定义可知(U,V,R)的关系矩

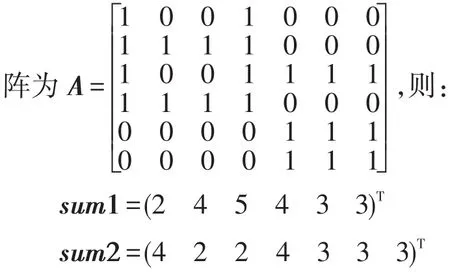
若X={x1,x2,x3,x4}，则X对应的矩阵为：

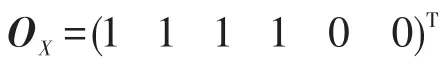
若Y={y1,y2,y3,y4}，则Y对应的矩阵为：

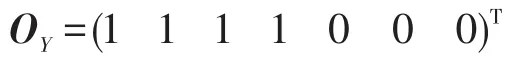
则A·OY=(2 4 2 4 0 0)T与 sum1中元素对应相比可知：

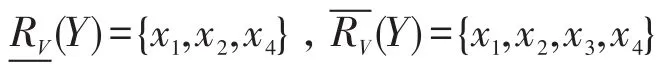
AT·OX=(4 2 2 4 1 1 1)T与 sum2 中元素对应相比可知：

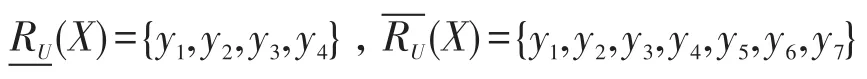
性质8设(U,V,R)和(V,W,S)是两个广义近似空间，它们的复合为(U,W,T)，其中U、V、W分别为n、m、l维非空有限论域，它们的关系矩阵分别为A=(R(xi,yk))n×m，B=(S(yk,zj))m×l，C=(T(xi,zj))n×l，则 C=A∘B。

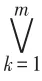
定义11在广义模糊近似空间(U,V,R)中，设U={x1,x2,…,xn}，V={y1,y2,…,ym}，称 M=(R(xi,yk))n×m为模糊关系矩阵，其中R(xi,yk)∈[0,1]。∀A∈F(U)，A对应的矩阵为OA=(A(x1)A(x2)…A(xn))。

性质9设(U,V,R)为广义模糊近似空间，U={x1,x2,…,xn}，V={y1,y2,…,ym}，模糊关系矩阵为 M=(R(xi,yk))n×m，则∀A∈F(U)，B∈F(U)，A和B的下近似和上近似对应的矩阵分别为：

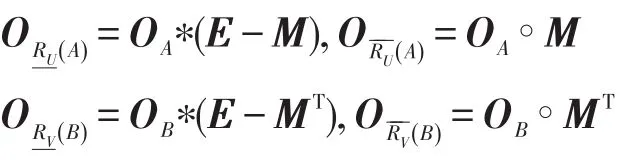
其中E表示任一元素都是1的矩阵。

证明首先证明

先证 ORU(A)=OA∗(E-M)。∀yk∈V，有(A)(yk)=(A)(yk)={A(x)∨(1-R(x,yk))},而 OA∗(E-M)中第k列元素为(A(xi)∨(1-R(xi,yk)))，故(A)(yk)={A(x)∨(1-R(x,yk))}=(A(xi)∨(1-R(xi,yk))得证。

例4续例2，由上述定义可知(U,V,R)的关系矩

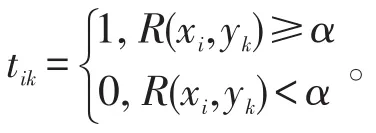
性质10设(U,V,R)和(V,W,S)是两个广义模糊近似空间，它们的复合为(U,W,T)，其中U、V、W分别为n、m、l维非空有限论域，它们的模糊关系矩阵分别 为A=(R(xi,yk))n×m，B=(S(yk,zj))m×l，C=(T(xi,zl))n×l，则C=A∘B。

证明证明过程和性质8的证明类似。

性质11设(U,V,R)和(V,W,S)是两个广义模糊近似空间，它们的复合为(U,W,T)，其中U、V、W分别为n、m、l维非空有限论域，模糊关系R、S、T的α 关系矩阵分别为 MR=(tik)m×n，MS=(tkj)n×l，MT=(tij)m×l，则MT=MR∘MS。

证明证明过程和性质8的证明类似。

5 结束语

本文对两个近似空间复合前后近似算子之间的关系作了进一步的探讨，进而根据关系的矩阵表示和矩阵运算对近似空间中的一些运算用矩阵进行了表示。由于矩阵是一种高效并且可计量化的工具，本文所给出的矩阵方法使人们从另一视角加深对粗糙集的认识，也使得计算大大简化。

[1]Pawlak Z.Rough sets[J].International Journal of Computer and Information Sciences,1982,11(15):341-356.

[2]Yan Ruixia,Zheng Jianguo,Liu Jinliang,et al.Research on the model of rough set over dual-universes[J].Knowledge-Based Systems,2010,23(8):817-822.

[3]Guan J W,Bell DA,Guan Z.Matrix computation for information systems[J].Information Sciences,2001,131(1/4):129-156.

[4]Liu Guilong.The axiomatization of rough set upper approximate operation[J].Fundamental Informaticae,2006,69(3):331-342.

[5]Liu Guilong.Rough set theory based on two universal sets and its applications[J].Knowledge Based Systems,2010,23(2):110-115.

[6]Liu Guilong.The algebraic structures of generalized rough set theory[J].Information Sciences,2008,178(21):4105-4113.

[7]Li Zhongran,Shu Lan.Matrix computation for upper and lower approximations of fuzzy rough sets[J].Computer Technology and Development,2015,25(4):10-12.

[8]Yao Y Y.Constructive and algebraic methods of the theory of rough sets[J].Information Sciences,1998,109(1):21-47.

[9]Zhang Junbo,Li Tianrui,Ruan Da,et al.Rough sets based matrix approaches with dynamic attribute variation in set-valued information systems[J].International Journal of Approximate Reasoning,2012,53(4):620-635.

[10]Wang Shiping,Zhu William,Zhu Qingxin,et al.Characteristic matrix of covering and its application to Boolean matrix decomposition[J].Information Sciences,2014,263(3):186-197.

[11]Liu Caihui,Miao Duoqian.Algorithm of upper and lower approximations based on matrix[J].Application Research of Computers,2011,28(5):1628-1630.

[12]Zhang Wenxiu,Wu Weizhi,Liang Jiye,et al.Rough set theory and method[M].Beijing:Science Press,2001.

[13]Yang Lunbiao,Gao Yingyi.Principle and application of fuzzy mathematics[M].Guangzhou:South China University of Technology Press,2005.

[14]Dubois D,Prade H.Rough fuzzy sets and fuzzy rough sets[J].International Journal of General Systems,1990,17(2/3):191-209.

[15]Sun Wenxin.Fuzzy rough set models over two universes and multi-granulation[D].Chongqing:Chongqing University of Technology,2013.

[16]Mi Jusheng,Zhang Wenxiu.Indirect learning based on rough set theory[J].Computer Science,2002,29(6):96-97.

附中文参考文献：

[7]李中然,舒兰.模糊粗糙集的上下近似的矩阵计算[J].计算机科学与发展,2015,25(4):10-12.

[11]刘财辉,苗夺谦.基于矩阵的粗糙集上、下近似求解算法[J].计算机应用研究,2011,28(5):1628-1630.

[12]张文修,吴伟志,梁吉业,等.粗糙集理论与方法[M].北京:科学出版社,2001.

[13]杨纶标,高英仪.模糊数学原理与应用[M].广州:华南理工大学出版社,2005.

[15]孙文鑫.双论域与多粒度模糊粗糙集模型研究[D].重庆:重庆理工大学,2013.

[16]米据生,张文修.基于粗糙集的间接学习[J].计算机科学,2002,29(6):96-97.

Matrix Representation of Composition ofApproximation Spaces*

YAOAimeng+,MI Jusheng
College of Mathematics and Information Science,Hebei Normal University,Shijiazhuang 050024,China
+Corresponding author:E-mail:yaoaimeng2015@163.com

YAO Aimeng,MI Jusheng.Matrix representation of composition of approximation spaces.Journal of Frontiers of Computer Science and Technology,2017,11(8)：1347-1353.

This paper mainly discusses the problem about calculating the upper and lower approximates of rough set in approximation space.Because a relation can be represented by a matrix and matrix operations are simple and intuitive,this paper proposes the calculation of the upper and lower approximates in rough set based on relation matrix and matrix operations.Firstly,this paper studies the compositions of two generalized approximation spaces and two generalized fuzzy approximation spaces,discusses the relationships between the operators in the composite approximation space and the two original approximation spaces,and shows that the generalized fuzzy approximation space is the further promotion of the generalized approximation space.Then,according to the matrix representation and the operation of the relation,this paper describes some operations and related properties in approximation space by matrix.Finally,this paper introduces the calculation of the upper and lower approximations of rough set in approximation space in matrix method.The theoretical proof shows that the matrix method is feasible and effective.

approximation space;composition;rough set;fuzzy set;matrix

g was born in 1966.He

the Ph.D.degree in applied mathematics from Xi'an Jiaotong University in 2003.Then he was a post-doctoral fellow at the Chinese University of Hong Kong.Now he is a professor and Ph.D.supervisor at Hebei Normal University.His research interests include rough sets,concept lattices and approximate reasoning,etc. 米据生（1966—），男，河北宁晋人，2003年于西安交通大学应用数学专业获得博士学位，随后在香港中文大学从事博士后研究，现为河北师范大学教授、博士生导师，主要研究领域为粗糙集，概念格，近似推理等。

YAO Aimeng was born in 1992.She is an M.S.candidate at Hebei Normal University.Her research interests include rough set and approximate reasoning,etc.姚爱梦（1992—），女，河北保定人，河北师范大学硕士研究生，主要研究领域为粗糙集，近似推理等。

A

：O236

*The National Natural Science Foundation of China under Grant Nos.61573127,61502144,61300121,61472463(国家自然科学基金);the Natural Science Foundation of Hebei Province under Grant No.A2014205157(河北省自然科学基金);the Training Program for Leading Talents of Innovation Teams in the Universities of Hebei Province under Grant No.LJRC022(河北省高校创新团队领军人才培育计划项目);the Natural Science Foundation of Higher Education Institutions of Hebei Province under Grant No.QN2016133(河北省高等学校自然科学基金);the Doctor Science Foundation of Hebei Normal University under Grant No.L2015B01(河北师范大学博士基金).

Received 2016-05,Accepted 2016-08.

CNKI网络优先出版:2016-08-15,http://www.cnki.net/kcms/detail/11.5602.TP.20160815.1659.016.html

ISSN 1673-9418 CODEN JKYTA8

Journal of Frontiers of Computer Science and Technology 1673-9418/2017/11(08)-1347-07

10.3778/j.issn.1673-9418.1605041

E-mail:fcst@vip.163.com

http://www.ceaj.org

Tel:+86-10-89056056

摘 要：针对近似空间中粗糙集上、下近似的求解问题，根据关系的矩阵表示和矩阵运算具有简便直观的特点，提出了利用矩阵方法对近似空间中粗糙集上、下近似进行计算。通过研究广义近似空间的复合和广义模糊近似空间的复合问题，首先对复合近似空间的算子和原来近似空间中的算子之间的关系作进一步的探讨，并说明了广义模糊近似空间的复合是广义近似空间复合的进一步推广；进而根据关系的矩阵表示和矩阵运算对近似空间中的一些运算以及相应的性质用矩阵进行了表示；最后对近似空间中粗糙集上、下近似的求解问题，也用矩阵方法进行了计算，理论证明结果显示了该方法是可行有效的。