格值信息系统的知识分辨度与信息熵*
张晓燕,史德容,魏 玲
1.西北大学 数学学院,西安 710127
2.重庆理工大学 数学与统计学院,重庆 400054
格值信息系统的知识分辨度与信息熵*
张晓燕1,2,史德容2,魏 玲1+
1.西北大学 数学学院,西安 710127
2.重庆理工大学 数学与统计学院,重庆 400054
格值信息系统;知识分辨度;信息熵;知识颗粒
1 格值信息系统
1.1 预备知识
粗糙集理论[1-2]是近年发展起来的一种处理不精确性、不确定性和模糊知识的软计算工具,已经在人工智能、故障检测、数据挖掘、医疗诊断、股票数据分析、模式识别、智能信息处理等领域得到了普遍的应用。经典粗糙集是以完备信息系统[3]为研究对象,以等价关系(满足自反性、对称性、传递性)为基础,通过等价关系将论域分成互不相交的等价类,划分越细,知识越丰富,信息越充分。
粗糙集模型[4]中的知识表达是通过信息系统[5]被认知的。相当于一个关系表,信息系统是一个反映对象与属性之间关系的数据表。实际上,信息系统就是一个三元数组(U,A,F),其中U是有限非空的对象集;A是有限非空的属性集;F是一个从对象到属性的映射。
在经典的信息系统中,属性值域是单一的实数域。随着粗糙集理论的发展,又提出了集值信息系统,即属性值都是集合。接着对属性值域为模糊集的信息系统进行了研究。这些信息系统的属性值域都是单一的,而在某些现实问题中,可能出现某些属性值是实数值,有些是集合值或区间值等[6]。因此,就顺势提出了背景最为广泛的格值信息系统[5,7-8]。在此信息系统中若有多个优势关系[9-10](知识)生成的多个优势类(知识颗粒),可用优势关系的粗细来叙说。而一个细优势关系生成的知识颗粒比一个粗优势关系生成的知识颗粒小,此时知识分辨能力强。基于此,本文把知识分辨度与信息熵[11-16]引进到格值信息系统中,通过研究发现,知识的分辨度越大表明知识的分辨能力越强,知识的分辨度越小表明知识的分辨能力越弱,而信息熵有着与之一致的结论。
1.2 格值信息系统相关定义
格值信息系统是一种知识表达系统,它区别于经典的知识表达系统,格值信息系统的属性取值域均是格值的。下面介绍格值信息系统的相关概念。
定义1[5]称一个四元数组L≥=(U,A,V,F)为格值信息系统,若U={x1,x2,…,xn}为对象集,A={a1,a2,…,am}为属性集,V=Va,Va是条件属性a的值域,是具有最大元1和最小元0的有限格,≥表示Va上的偏序关系;F={f:U→V}为对象属性值映射,也称信息函数,有f(xi,a)∈Va,∀a∈A。
注:本文以偏序关系为基础得到一种新的关系——优势关系。
设L≥=(U,A,V,F)是一个格值信息系统,对于任意属性子集B⊆A,给出二元关系:
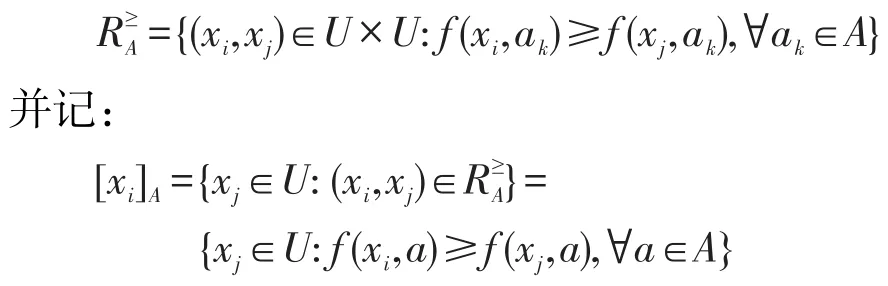
为xi关于条件属性集A的偏序类。
2 格值信息系统的知识分辨度
序信息系统[10]中知识的粒度可以反映知识的分辨能力,知识的粒度越大表明知识的分辨能力越弱,知识的粒度越小表明知识的分辨能力越强。同样的,本文通过知识的粒度来研究格值信息系统中知识的分辨能力,首先介绍知识粒度的相关概念,然后再引入知识分辨度的定义。
定义2[16]设L≥=(U,A,V,F)为格值信息系统,R≥为L≥上的优势关系,记:
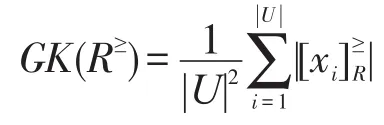
称 GK(R≥)为知识R≥的粒度。
定义3设L≥=(U,A,V,F)为格值信息系统,R≥为L≥上的优势关系,记:
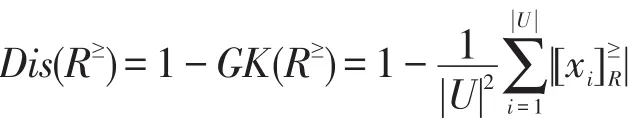
称Dis(R≥)为知识R≥的分辨度。
定理1(粗糙不变性)设L≥=(U,A,V,F)为格值信息系统,R≥、S≥为L≥上的优势关系。若|U/R≥|=|U/S≥|,且存在一一对应h:U/R≥→U/S≥,使得则 Dis(R≥)=Dis(S≥)。
证明由知识粒度的粗糙不变性可知GK(R≥)=GK(S≥),再由定义3直接获证。
推论1设L≥=(U,A,V,F)为格值信息系统,R≥、S≥为 L≥上的优势关系。若R≥=S≥,则 Dis(R≥)=Dis(S≥)。
定理2(单调性)设L≥=(U,A,V,F)为格值信息系统,R≥、S≥为 L≥上的优势关系。若R≥≤S≥,则Dis(R≥)≥Dis(S≥)。
证明由于R≥≤S≥,故对任意的x∈U,有,于是有:
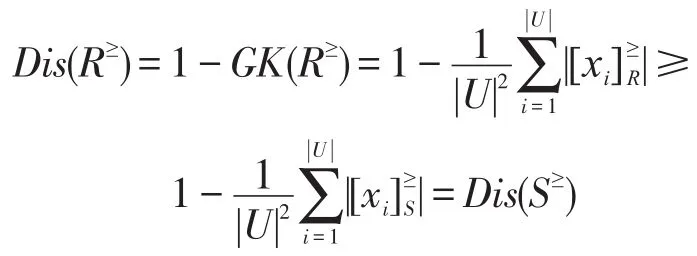
即 Dis(R≥)≥Dis(S≥)。
推论2设L≥=(U,A,V,F)为格值信息系统,R≥、S≥为 L≥上的优势关系。若R≥<S≥,则Dis(R≥)>Dis(S≥)。
推论3设L≥=(U,A,V,F)为格值信息系统,R≥、S≥为 L≥上的优势关系。若R≥≤S≥,且 Dis(R≥)=Dis(S≥),则R≥=S≥。
定理2、推论2和推论3说明,分辨度随着知识颗粒的变大、分类的变粗而单调减小,或者随知识颗粒的变小、分类的变细而单调增加。
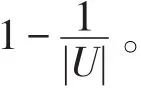
证明由于,故有:
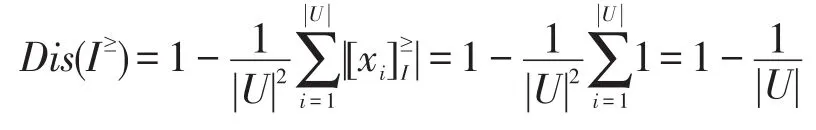
定理4(最小值)设L≥=(U,A,V,F)为格值信息系统,R≥为 L≥上的优势关系。若R≥=δ≥,则知识R≥的分辨度达到最小值0。
证明由于,故有:
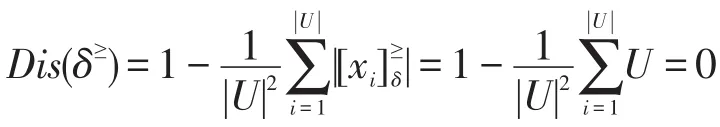
即 Dis(δ≥)=0。
定理5设L≥=(U,A,V,F)为格值信息系统,R≥为L≥上的优势关系,则知识R≥的分辨度满足:
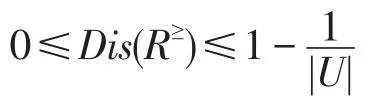
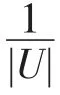
证明由定理3、定理4直接可得。
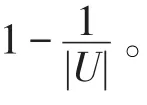
定理6(细化性)设L≥=(U,A,V,F)为格值信息系统,R≥为 L≥上的优势关系。若R′≥是将U/R≥中的某个知识颗粒细化成两个知识颗粒后形成的新的优势关系,且U/R′≥中其他知识颗粒与U/R≥中相同,则有Dis(R′≥)≥Dis(R≥)。
证明设U/R≥中的某个知识颗粒分解成两个知识颗粒(不妨设i<j),其中,且,于是:
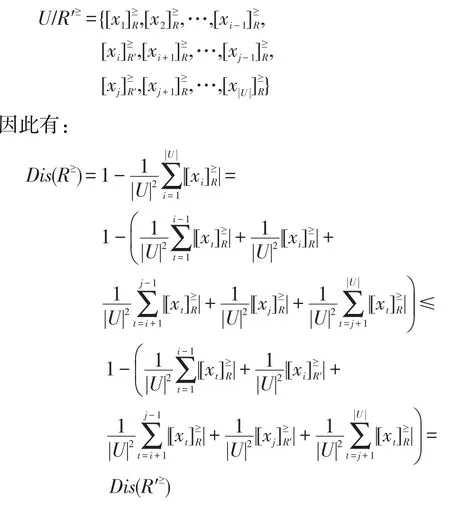
即 Dis(R′≥)≥Dis(R≥)。
推论4设L≥=(U,A,V,F)为格值信息系统,R≥为L≥上的优势关系,且R′≥是将U/R≥中的某个知识颗粒分解形成的新的优势关系,若R′≥≤R≥,则Dis(R′≥)≥Dis(R≥)。
定理7(粗化性)设L≥=(U,A,V,F)为格值信息系统,R≥为 L≥上的优势关系,若R″≥是将U/R≥中的某两个知识颗粒粗化成一个知识粒度后形成的新的优势关系,且U/R″≥中其他知识颗粒与U/R≥中的相同,则有 Dis(R≥)≥Dis(R″≥)。
证明设U/R≥中的某两个知识颗粒合成一个知识颗粒(不妨设i,j<k),其中,于是:
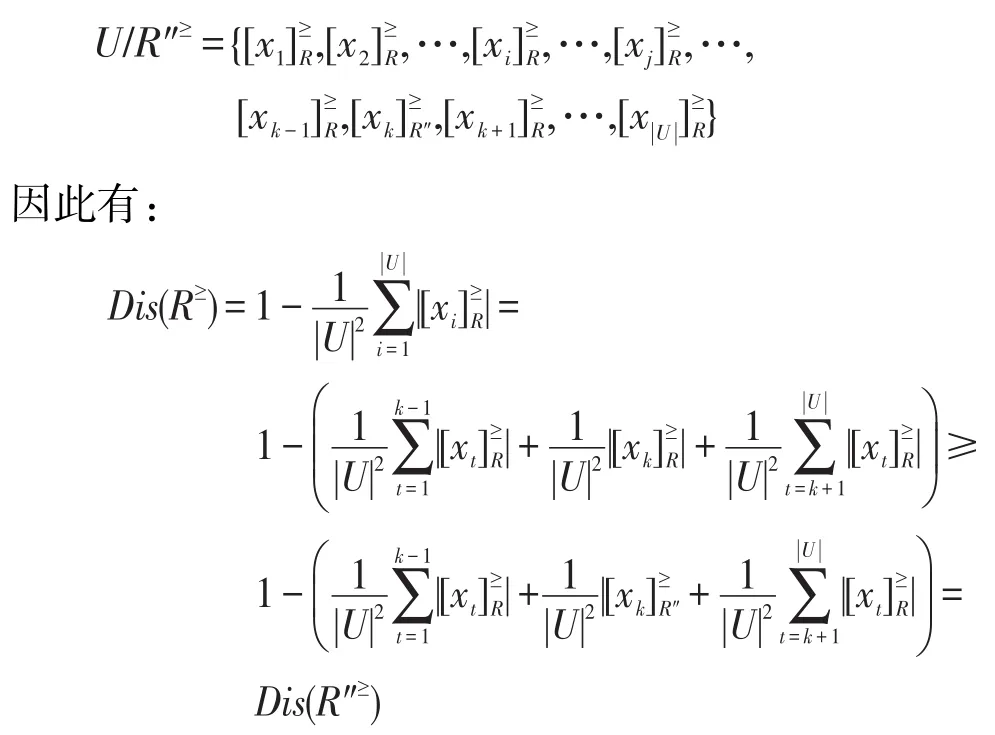
即 Dis(R≥)≥Dis(R″≥)。
推论5设L≥=(U,A,V,F)为格值信息系统,R≥为L≥上的优势关系,且R″≥是将U/R≥中的知识颗粒合并形成的新的优势关系,若R≥≤R″≥,则 Dis(R≥)≥Dis(R″≥)。
由上面结论可知知识颗粒的细化和粗化对知识分辨度的大小有很大的影响。随着知识颗粒的细化,知识分辨度变大,当每个知识颗粒中只有一个元素时,知识分辨度达到最大值,此时的知识是最精确的,而随着知识颗粒的粗化,知识分辨度将逐渐变小,当只有一个知识颗粒即论域本身时,知识分辨度达到最小值,此时的知识是最粗糙的。因此在实际问题中要尽可能细化知识颗粒来获得精确的认识,通过粗化知识颗粒使问题简单化。
3 格值信息系统的知识信息熵
本文在粗糙集理论中利用集合的补定义了一种新的熵,用这种方法给出了格值信息系统的信息熵,并对其性质进行了讨论。
定义4设L≥=(U,A,V,F)为格值信息系统,R≥为L≥上的优势关系,记:
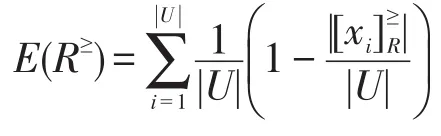
称E(R≥)为知识R≥的信息熵。
定理8设L≥=(U,A,V,F)为格值信息系统,R≥为L≥上的优势关系,则R≥的信息熵E(R≥)与知识粒度GK(R≥)之间的关系为:
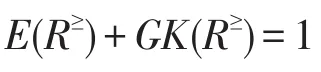
证明R≥为L≥上的优势关系,且粒度分类为,由定义4可得:
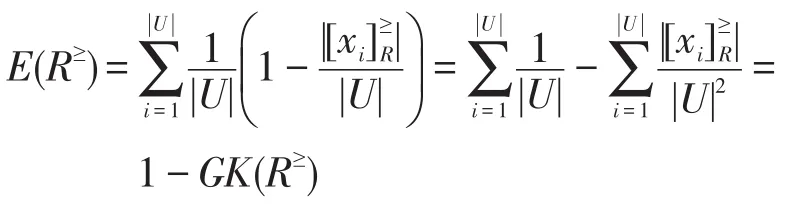
即E(R≥)+GK(R≥)=1。
推论6设L≥=(U,A,V,F)为格值信息系统,R≥为L≥上的优势关系,则R≥的信息熵E(R≥)与知识分辨度Dis(R≥)之间的关系为:
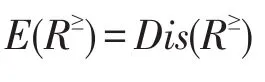
推论7设L≥=(U,A,V,F)为格值信息系统,R≥、S≥为L≥上的优势关系,则R≥的信息熵满足:
(1)(粗糙不变性)若|U/R≥|=|U/S≥|,且存在一一对应h:U/R≥→U/S≥,使得,则E(R≥)=E(S≥)。
(2)(单调性)若R≥≤S≥,则E(R≥)≥E(S≥)。
(3)(有界性和最值性)信息熵E(R≥)满足:
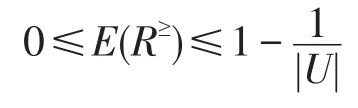
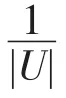
(4)(细化性)若R′≥是将U/R≥中的某个知识颗粒细化成两个知识颗粒后形成的新的优势关系,且U/R′≥中其他知识颗粒与 U/R≥中相同,则有E(R′≥)≥E(R≥)。
(5)(粗化性)若R″≥是将U/R≥中的某两个知识颗粒粗化成一个知识粒度后形成的新的优势关系,且U/R″≥中其他知识颗粒与U/R≥中的相同,则有E(R≥)≥E(R″≥)。
4 实例分析

Table1 Alattice-valued information system表1 给定格值信息系统
表中U={xi|i=1,2,…,6}是对象集,A={a1,a2,a3}是属性集,并且该格值信息系统是基于优势关系R≥的,其中:
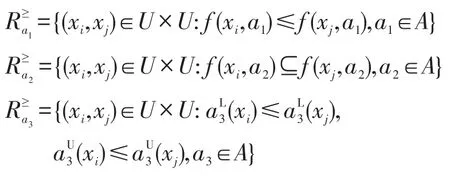

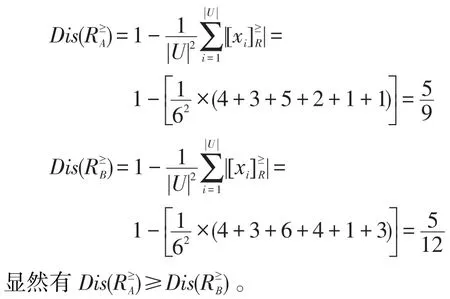
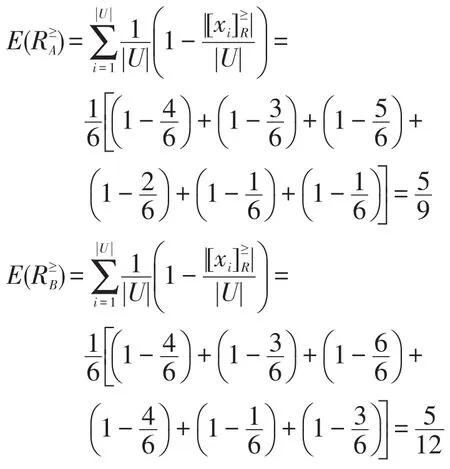
对比分辨度和信息熵的计算结果可知:
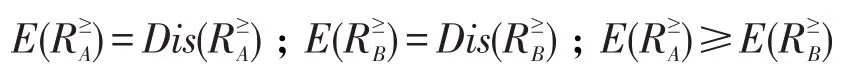
由这个实例证实了分辨度与知识粒度,信息熵与知识粒度,分辨度与信息熵的关系,而且知识的分辨度与信息熵是相同的,因此它们都可以用来反映格值信息系统中知识的颗粒和分类程度,分辨度与信息熵则从侧面反映了格值信息系统中知识颗粒对知识的影响。
5 结束语
生产生活中许多信息系统是基于优势关系建立起来的。梁吉业等人成功地建立了经典粗糙集下信息系统的熵理论。本文把知识分辨度、知识信息熵引入到格值信息系统中,研究了它们各自的性质,并讨论了它们之间的关系,证明了二者随着知识颗粒的细化而单调增加,粗化而单调减小的结论,而且知识的分辨度与信息熵是相同的。进一步用具体的实例验证了知识分辨度和信息熵的性质和关系,保证了其准确性。
[1]Pawlak Z.Rough sets:theoretical aspects of reasoning about data[M].Boston:KluwerAcademic Publishers,1991.
[2]Pawlak Z,Grzymala-Busse J,SlowinskiR,et al.Rough sets[J].Communication of theACM,1995,38(11):88-95.
[3]Liang Jiye,Xu Zongben.Uncertainty measures of roughness of knowledge and rough sets in incomplete information systems[C]//Proceedings of the 3rd World Congress on Intelligent Control and Automation,Hefei,China,Jun 28-Jul 2,2000.Piscataway,USA:IEEE,2000,4:2526-2529.
[4]Zhang Xiaohong,Pei Daowu,Dai Jianhua.Fuzzy mathematics and the rough set theory[M].Beijing:Tsinghua University Press,2013.
[5]Zhang Wenxiu,Liang Yi,Wu Weizhi.Information system and knowledge discovery[M].Beijing:Science Press,2003.
[6]Yu Jianhang,Xu Weihua.Incremental knowledge discovering in interval-valued decision information system with the dynamic data[J].International Journal of Machine Learning and Cybernetics,2015,515:1-16.
[7]Huang Jiazeng,Cai Xiangyun.Aknowledge reduction method based on rough sets and lattice-valued information systems[J].Journal of Computer Knowledge and Technology,2008,2(18):135-137.
[8]Zhang Xiaoyan,Wei Ling,Xu Weihua.Attributes reduction and rules acquisition in an lattice-valued information system with fuzzy decision[J].International Journal of Machine Learning and Cybernetics,2017,8(1):135-147.
[9]Grecos MB,SlowinskiR.Rough approximation of preference relation by dominance relations[J].European Journal of Operational Research,1999,117(1):63-68.
[10]Xu Weihua.Ordered information systems and rough sets theory[M].Beijing:Science Press,2013.
[11]Liang Jiye,Chin K S,Dang Chuangyin,et al.Anew method for measuring uncertainty and fuzziness in rough set theory[J].International Journal of General Systems,2002,31(4):331-342.
[12]Wang Guoying,Yu Hong,Yang Dachun.Decision table reduction based on conditional information entropy[J].Chinese Computers,2002,25(7):759-766.
[13]Liang Jiye,Shi Zhongzhi.The information entropy,rough entropy and knowledge granulation in rough set theory[J].International Journal of Uncertainty Fuzziness and Knowledge-Based Systems,2004,12(1):37-46.
[14]Liang Jiye,Shi Zhongzhi,Li Deyu,et al.Information entropy,rough entropy and knowledge granulation in incomplete information systems[J].International Journal of General Systems,2006,35(6):641-654.
[15]Zhang Xiaoyan,Xu Weihua.Entropy of knowledge and rough set in ordered information systems[J].Computer Engineering andApplications,2007,43(27):62-65.
[16]Xu Weihua,Zhang Xiaoyan,Zhang Wenxiu.Knowledge granulation,knowledge entropy and knowledge uncertainty measure in ordered information systems[J].Applied Soft Computing,2009,9(4):1244-1251.
附中文参考文献:
[4]张小红,裴道武,代建华.模糊数学与Rough集理论[M].北京:清华大学出版社,2013.
[5]张文修,梁怡,吴伟志.信息系统与知识发现[M].北京:科学出版社,2003.
[7]黄加增,蔡翔云.一种基于粗集的格值信息系统的知识约简方法[J].电脑知识与技术,2008,2(18):135-137.
[10]徐伟华.序信息系统与粗糙集[M].北京:科学出版社,2013.
[12]王国胤,于洪,杨大春.基于条件信息熵的决策表约简[J].计算机学报,2002,25(7):759-766.
[15]张晓燕,徐伟华.序信息系统的知识粗糙熵与粗集粗糙熵[J].计算机工程与应用,2007,43(27):62-65.

SHI Derong was born in 1991.She is an M.S.candidate at Chongqing University of Technology.Her research interest is the mathematical foundation of artificial intelligence.史德容(1991—),女,重庆人,重庆理工大学硕士研究生,主要研究领域为人工智能的数学基础。

WEI Ling was born in 1972.She is a professor and Ph.D.supervisor at Northwest University.Her research interests include concept lattice and rough set,etc.魏玲(1972—),女,陕西西安人,博士,西北大学教授、博士生导师,主要研究领域为概念格,粗糙集等。
欢迎订阅2018年《计算机科学与探索》、《计算机工程与应用》
《计算机科学与探索》为月刊,大16开,单价48元,全年12期总订价576元,邮发代号:82-560。
邮局汇款地址:
北京619信箱26分箱《计算机科学与探索》编辑部(收) 邮编:100083
《计算机工程与应用》为半月刊,大16开,每月1日、15日出版,单价45元,全年24期总订价1080元,邮发代号:82-605。
邮局汇款地址:
北京619信箱26分箱《计算机工程与应用》编辑部(收) 邮编:100083
欢迎到各地邮局或编辑部订阅。个人从编辑部直接订阅可享受8折优惠!
发行部
电话:(010)89055541
Knowledge Resolution and Information Entropy in Lattice-Valued Information Systems*
ZHANG Xiaoyan1,2,SHI Derong2,WEI Ling1+
1.School of Mathematics,Northwest University,Xi'an 710127,China
2.School of Mathematics and Statistics,Chongqing University of Technology,Chongqing 400054,China
+Corresponding author:E-mail:wl@nwu.edu.cn
ZHANG Xiaoyan,SHI Derong,WEI Ling.Knowledge resolution and information entropy in lattice-valued information systems.Journal of Frontiers of Computer Science and Technology,2017,11(8):1340-1346.
In dealing with practical issues,it is generally possible to obtain accurate understanding through the refinement of knowledge particles.On the contrary,the problem can be simplified by coarse knowledge particles.This paper introduces the concepts of knowledge resolution and information entropy to study the resolution ability of knowledge in lattice-valued information systems.By some properties,it can be proved that both of them gradually become lager with the refinement of knowledge particles,smaller with the coarsening of knowledge particles.An instance result shows that the knowledge resolution and information entropy are greater,the ability of knowledge resolution is stronger.Furthermore,the relationship between knowledge resolution and information entropy,which can be used to reflect the particles of knowledge and the degree of classification in lattice-valued information systems,states that they are the same.In addition,the influence of knowledge particles on knowledge is reflected from the side.These conclusions provide theoretical basis for the knowledge discovery of lattice-valued information systems.
lattice-valued information system;knowledge resolution;information entropy;knowledge particles
2016-05,Accepted 2016-08.
A
:TP18
*The National Natural Science Foundation of China under Grant Nos.61472463,61402064(国家自然科学基金);the Graduate Innovation Foundation of Chongqing University of Technology under Grant No.YCX2015227(重庆理工大学研究生创新基金).
CNKI网络优先出版:2016-08-01,http://www.cnki.net/kcms/detail/11.5602.TP.20160801.1406.006.html
ISSN 1673-9418 CODEN JKYTA8
Journal of Frontiers of Computer Science and Technology 1673-9418/2017/11(08)-1340-07
10.3778/j.issn.1673-9418.1605044
E-mail:fcst@vip.163.com
http://www.ceaj.org
Tel:+86-10-89056056
摘 要:在处理实际问题时,一般会尽可能通过细化知识颗粒获得精确的认识,相反地,经过粗化知识颗粒来使问题得以简单化。在格值信息系统中引入知识分辨度和信息熵的概念来研究知识的分辨能力。通过研究它们的有关性质,证明了二者随着知识颗粒的细化逐渐变大,粗化而逐渐变小的结论。通过对实例的研究得到知识的分辨度和信息熵越大表明知识的分辨能力越强,知识的分辨度和信息熵越小表明知识的分辨能力越弱。进一步通过它们之间的关系发现知识的分辨度与信息熵是相同的,因此它们都可以用来反映格值信息系统中知识的颗粒和分类程度,都从侧面反映了格值信息系统中知识颗粒对知识的影响。这些结论为格值信息系统的知识发现奠定了一定的理论基础。

