基于遗传算法的DNA序列聚类可靠性评估

孙 杰, 李 重

(浙江理工大学理学院，杭州 310018)



基于遗传算法的DNA序列聚类可靠性评估

孙 杰, 李 重

(浙江理工大学理学院，杭州 310018)

聚类分析是分子生物学家推断同源序列进化关系的常用技术,评估聚类的可靠性是聚类分析的重要内容。Bootstrap是评估聚类可靠性的一种统计方法，它替换DNA序列的所有核苷酸碱基以进行采样分析。在Bootstrap方法的基础上，提出了一种评估DNA序列聚类可靠性的改进方法。该方法首先按照一定比例随机抽取原始DNA序列的部分碱基，然后对抽取的每个碱基利用遗传算法进行替换。提出的方法考虑了碱基之间的相关性，得到的样本更接近于原始序列，且更符合生物渐进进化的结果。使用该方法对DNA序列聚类构建的进化树进行可靠性评估。实验结果发现可靠性评估的准确率得到了提高，表明该方法可行、有效。

DNA序列；聚类分析；进化树；Bootstrap；可靠性

0 引 言

序列比对[1]通过排列DNA、RNA或蛋白质序列的方式，识别可以描述序列间的功能、结构以及进化关系的相似序列区域[2]。它一般决定了许多生物信息学技术及程序的分析结果[3]，影响着很多序列比较研究的结论和生物解释，是DNA聚类分析等研究中的一个重要内容。

随着基因数量的增加，对它们进行有效分析变得更加困难，而聚类分析是解决这一问题的实用方法。聚类分析能够有效处理基因表达数据，是生物多样性研究经常用到的一种方法。在DNA聚类分析中，聚类是把相似序列以静态分类的方法划分入不同的组中，使得组内的序列比不同组中的更相近。通常，聚类方法可以分为划分聚类[4]和层次聚类[5]。划分聚类方法根据一些优化准则将数据分成M(通常是预先设定的值)组。k-means以及k-medoids方法是划分聚类中比较典型的方法。层次聚类算法通过构建一个嵌套聚类的分层集合实现聚类。在分层集合中最顶层的类包含所有的数据对象，而最底层的类只包含单个的数据对象[6]。层次聚类通过在层次结构的每个层级上显示合并的两个集群，同时显示集群之间的距离，提供了一种自然的形式来图形化表示数据集。

聚类可靠性(也称确定性或稳定性)用于描述聚类分析的置信度。如何衡量两个聚类的相似度是评估聚类可靠性的关键内容。Bootstrap是由Felsenstein[7]引入的一种评估聚类可靠性的方法，现已被生物学家广泛接受和使用。该方法是一种非参数统计方法，用于评估统计估计的准确性。Bootstrap通过垂直替换的方式获得样本，可以模拟生物进化过程中序列碱基的置换、插入和删除，它对分子序列的一般做法是重采样整个序列[8]。通过执行Bootstrap得到的聚类可靠性通常以百分比的形式显示在树状图中[9]。另外，在聚类可靠性评估中，还有一些基于Bootstrap的改进方法，如Block Bootstrap方法[10]、Subsampling Bootstrap方法等。

本文提出了一种评估DNA序列聚类可靠性的方法。该方法在标准Bootstrap方法的基础上，进行了如下改进：按照一定的比率在DNA序列中抽取碱基数据；对抽取的每个碱基构建一定长度的碱基窗口并应用遗传算法对碱基进行置换。本文采用该方法对不同物种(beta-globulin DNA sequences, H5N1，H5N2)的DNA序列聚类进行可靠性评估实验，以验证该方法的有效性。

1 方法设计

1.1 序列相似性分析

从比对序列数目的角度看，序列比对可划分为两类：双序列比对和多序列比对。双序列比对通常以动态规划算法为理论基础。一般动态规划算法可以扩展到多于两个序列的情况，但是随着核酸数据的增长，基于动态规划的多序列比对问题就会变得非常复杂，这时基于SP(逐对加和)比对模型的多序列比对就成了一个NP问题[11]。对多序列比对问题的研究仍然是一个具有挑战性的任务。启发式算法是当前大部分多序列比对所采用的算法。迭代比对和渐进比对是两种典型的基于启发式算法的多序列比对方法。

迭代比对算法以迭代方式优化多序列比对，逐步改进比对结果，直至不能获得更合理的比对结果。根据改进策略，迭代比对算法可以划分为确定型和随机型两种，其中确定型算法[12]最简单。Prrp[13]、隐马尔可夫模型(HMM)[14]、模拟退火[15]以及遗传算法[16]等是随机迭代算法中的典型方法。渐进比对算法根据序列间由近及远的进化关系，用双序列比对算法对序列或子比对结果进行比对，重复这一过程直至所有序列都得到比对。它的优点是所需时间较短、所占内存较少[17]。T-Coffee[18]和ClustalW[19]等是基于渐进比对算法并被广泛使用的多序列比对算法，其中使用最广的是ClustalW算法。

本文通过软件包MEGA用ClustalW算法先对DNA序列间的相似性进行了分析，然后使用适当的度量标准计算得到了DNA序列之间的距离矩阵。

1.2 Bootstrap改进方法

在得到不同物种DNA序列间的距离矩阵后，本文对DNA序列进行聚类分析，并通过相应树状图(进化树)直观地将进化关系显现出来。本文使用层次聚类中非加权组平均法(unweighted pair-group method with arithmetic mean,UPGMA)进行聚类，利用Bootstrap方法对构建的进化树的可靠性进行评估检验。

标准Bootstrap方法直接应用在生物序列聚类可靠性评估中存在两个缺点[20]。

首先，标准Bootstrap通过替换原始序列的所有核苷酸碱基得到新的样本，它假设这样得到的所有样本是等可能的。但是生物进化过程是渐进的，即进化后的DNA序列更接近于原始序列，因此标准的Bootstrap方法并不适合模拟DNA序列的进化过程。为了改善这一缺陷，Zhang等[6]提出了Subset Bootstrap方法：首先在原始数据矩阵中按设定比例随机抽取列(记录这些列的位置)的子集；然后，对抽取的列的子集应用标准的Bootstrap方法；最后将变化后的子集插回到原始数据矩阵中。插回的位置对应从原始数据矩阵中抽取时的位置，这样得到的新数据矩阵就是一个Subset Bootstrap样本。实际上Subset Bootstrap方法是通过在原始DNA序列中随机替换部分核苷酸碱基来实现生物进化模拟的，但是它忽略了一条DNA序列中核苷酸碱基之间的相关性。

其次，标准Bootstrap方法假设DNA序列之间的核苷酸碱基相互独立[8]。在生物信息学中，一个普遍规律是序列决定结构，结构决定功能。因此在序列中碱基间的排列关系对生物信息具有一定的影响。所以，假设一条DNA序列的核苷酸碱基之间具有独立性存在问题。Bootstrap在相关型数据上的应用是一个热点研究领域，这一领域的常用方法是Subsampling以及Block Bootstrap方法。Subsampling方法从原始序列随机选取一定长度的连续片段作为新样本。它具有相当普遍的实用性，但缺点是收敛速度较差[20]，并且样本长度小于原始序列长度。Block Bootstrap方法生成一个Block(连续序列片段)集合，每次从Block集合中随机选择一个Block替换原始序列中的部分片段。该方法对相关型数据很有用，但缺点是没有改变Block中的碱基。

由以上分析可知，Subsampling和Block Bootstrap都不是合适的重采样方法。

为了更合理地模拟自然进化，本文在进行重采样时仅改变原始DNA序列中一定比例的碱基，并且在置换碱基时将其临近碱基序列考虑进来。另外，本文在置换碱基时引入自然进化准则，使用遗传算法(genetic algorithm)模拟具有相关性碱基之间的变化过程。在模拟过程中，本文首先以某一待置换碱基为中心构建碱基窗口(一定长度的碱基序列)；然后对该碱基窗口应用遗传算法的选择、交叉和变异运算，以模拟生物序列的自然进化；最后对遗传运算结束后的碱基窗口依据适当原则选出碱基，以替换原始序列中的碱基。具体过程如下：

a) 计算采样比例：计算DNA序列两两之间的进化率(对齐的两序列不同碱基总数与序列长度的比值，长度不同时取短序列长度作为分母)Rij(i=1,2, …,n-1,j=i+1, …,n,n为序列的总数)，并计算Rij的平均值。本文取平均进化率作为采样比例。

b) 按照采样比例，从每条DNA序列中选取不同列的碱基。对选出的每个碱基构造碱基窗口，利用遗传算法置换这个碱基。具体操作如下：

b1) 对于从一条DNA序列中选出的每个碱基，构造碱基窗口W(左右各扩展一定个数碱基的连续序列片段)。从除W所在序列以外的每条序列中选出与W相似度(碱基窗口对齐后相同碱基的总数)最大的碱基窗口Wi(i=1, …,n-1)。将选出的n-1个碱基窗口作为遗传算法的初始种群。

b2) 对初始种群执行“选择”运算：设W所在序列与剩余序列的相似度总和为sum,与剩余序列中第i条序列的相似度为Si(i=1, …,n-1)。将比值Si/sum作为第i条序列中选出的窗口在初始种群中被选择的概率。“选择”运算选出的新种群与初始种群个数相同。

b3) 对选出的新种群进行“交叉”运算：在进行“交叉”之前要对碱基窗口进行编码。由于核苷酸碱基的种类只有A、T、G、C 4种，所以只需要2位二进制数即可对一个碱基编码。这样A、T、G、C可编码为00、01、10、11。

“交叉”是根据某一概率对随机配对的种群进行的。若碱基窗口长度为L，则编码序列长度为2L。令编码序列两个相邻碱基之间的位置为位点，则长为2L的编码序列有2L-1个位点。交叉位点可从1, …,2L-1中随机选取。本文采用单点交叉的方法进行交叉，即交换配对的编码序列交叉位点之后的二进制数据。

b4) 对“交叉”后的编码序列进行“变异”运算：“变异”运算根据某一变异概率进行。对于长为2L的编码序列，它的每个位置都有突变的可能，所以突变位点可从1, …,2L中随机选取。选出突变位点后将该位点的编码数值取反。

b5) 对数据解码，将编码序列恢复为碱基序列。循环执行步骤b2)，b3)，b4)。将最终得到的碱基窗口保存。

比较式(1)的计算结果与碱基编码转换成的4个十进制数值，选出最接近计算结果的十进制数值所对应的碱基。将所选的碱基替换W中心位置所对应的原始序列中的碱基。这样变换得到一个新的DNA序列样本。

(1)

其中：Vi为执行遗传运算后Wi中心位置碱基对应编码转换成的十进制数值。

c) 通过序列比对结果计算出相似距离矩阵。

d) 根据产生的相似距离矩阵进行聚类分析，并构建进化树。

改进Bootstrap方法的主要流程如图1所示。

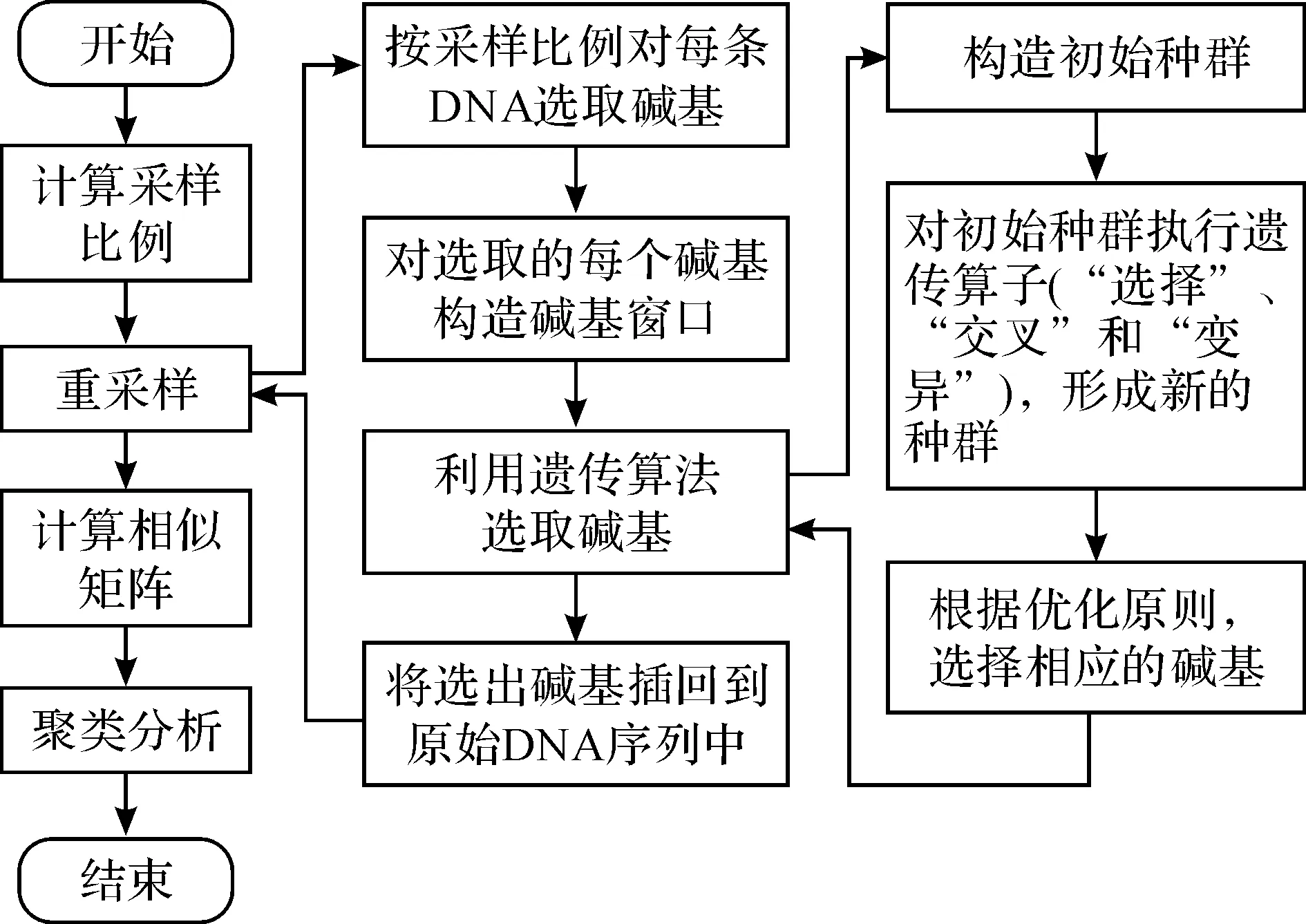
图1 改进的Bootstrap方法流程

1.3 聚类可靠性计算

本文在Bootstrap采样过程中，每次都对采样数据进行重新聚类并构建进化树。进化树的每个分支用DNA序列的子集表示。若采样总次数为S，某子集重复出现的次数为t，则比值t/S为该子集在统计检验中的有效性。具体来说，用Zi=(Zi1,Zi2, …,Zig)表示进化树中某一分支包含的DNA序列的子集，其中i= 1, …,m,m为聚类形成的进化树所包含的总分支数，g为DNA序列总数，Zi1,Zi2, …,Zig对应数据集中按序排列的DNA序列。Zig取值为0和1，0表示第i个子集中不包含第g条DNA序列， 1表示包含。用相同方法对原始数据集聚类并构建进化树，并用同样的方式进行表示。将采样数据与原始数据的集合表示进行比对，若有相同的分支出现，则将该分支对应的重复次数加1。在S次Bootstrap采样并重新聚类的过程中，记子集Zi出现的次数为t，则比值t/S可以表示进化树中第i条分支有效性的统计检验结果，即该分支的聚类可靠性。

2 结果和讨论

本文对给定的DNA序列分别应用标准Bootstrap、SubsetBootstrap以及本文方法进行了实验，并且对比了实验结果。实验中所用序列数据从NCBI网站[http://www.ncbi.nlm.nih.gov/]上选取。本文对3组实验数据进行了实验。实验数据1选取了8个物种的β-球蛋白基因的第一个外显子(Exon)，如表1所示，数据中各物种对应序列所含碱基个数介于86～105之间。为了完整地显示实验结果以及方便地评估聚类可靠性，实验数据2从109个H5N1病毒的HA(hemagglutinin)基因序列[6]中挑选了11个序列。所选序列的长度和序列码如表2所示。实验数据3是挑选自H5N2病毒的29条HA基因序列。所选序列的长度和序列码如表3所示。

表1 8个物种的β-球蛋白基因的第一个外显子(Exon)序列

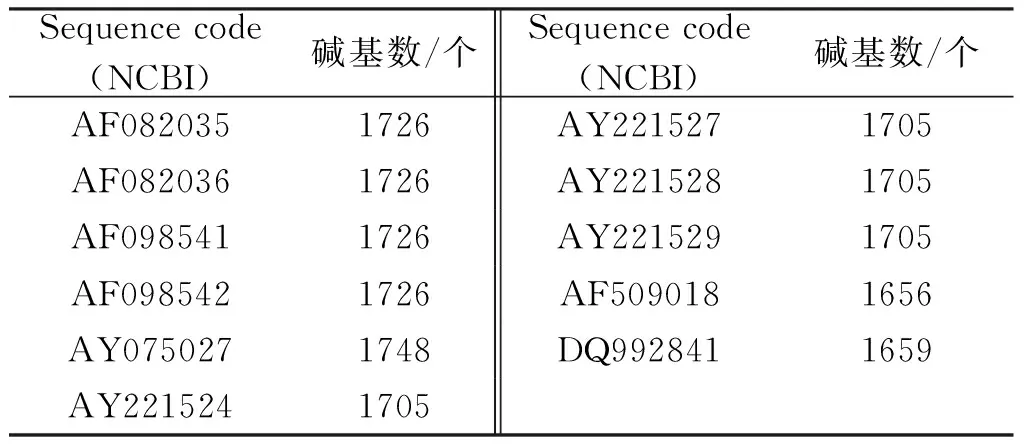
表2 11个H5N1病毒的HA基因序列

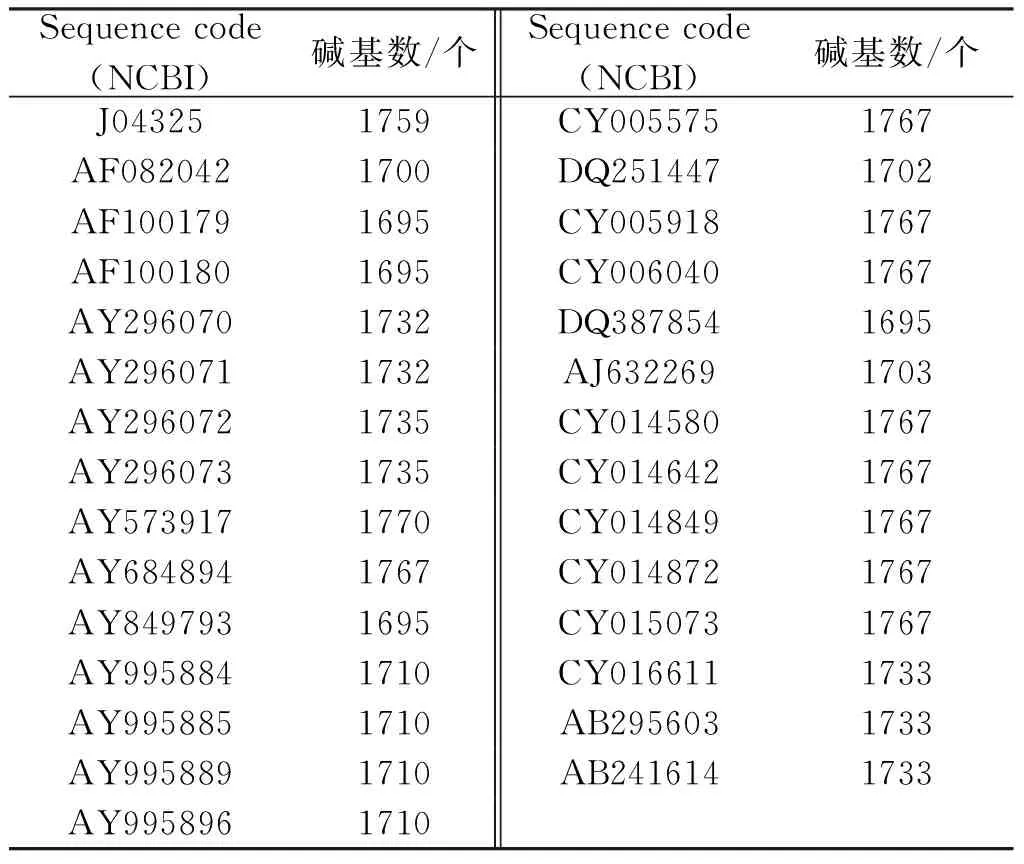
表3 29个H5N2病毒的HA基因序列

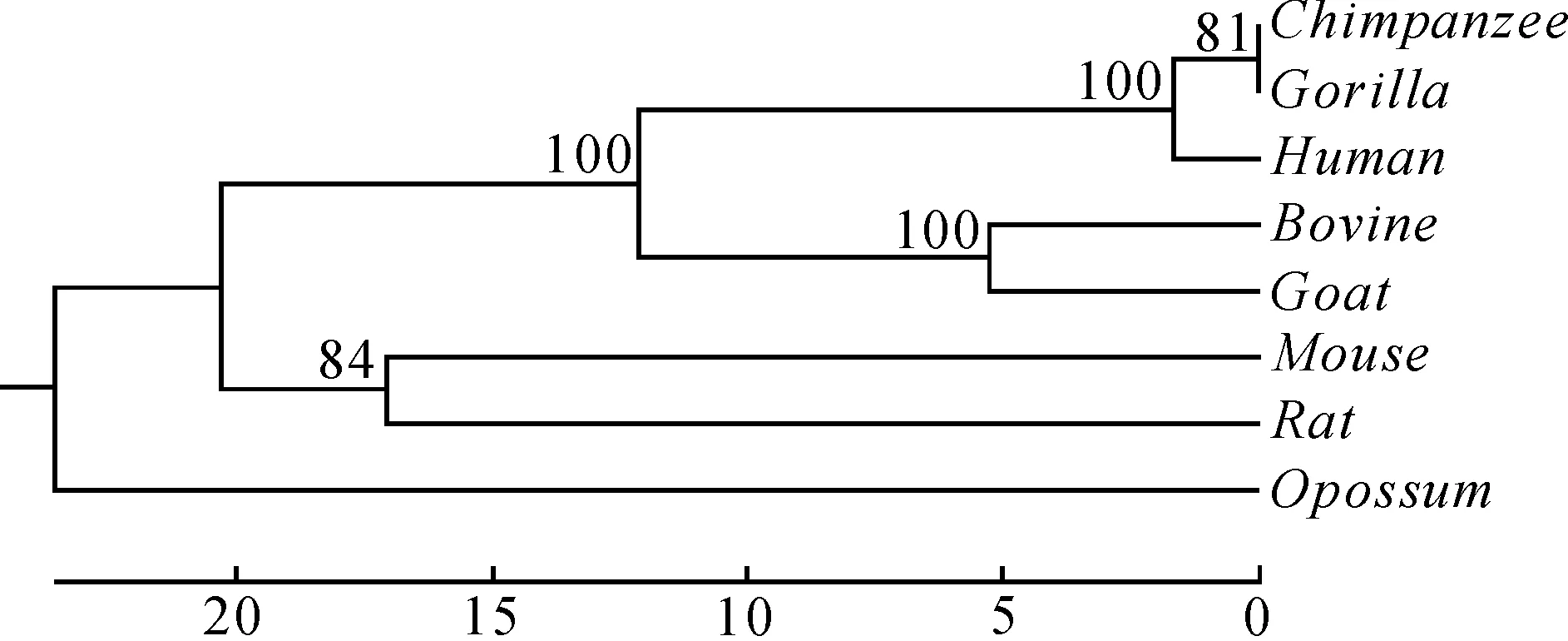
本文利用Mega软件，首先使用UPGMA方法对基于ClustalW得到的距离矩阵构建了进化树，然后用3种不同Bootstrap方法计算了聚类可靠性，并对可靠性结果进行了比较。图2(a)、图3(a)为分别对实验数据1和2应用标准的Bootstrap方法构建的进化树。图2(b)、图3(b)分别为对实验数据1和2使用Subset Bootstrap方法构建的进化树。图2(c)、图3(c)分别为对实验数据1和2使用本文提出方法得到的进化树。图4为对实验数据3使用本文提出方法得到的进化树。表4比较了不同Bootstrap方法得到的聚类可靠性平均值。由表4可以看出，本文方法所得可靠性结果优于标准Bootstrap方法和Subset Bootstrap方法。

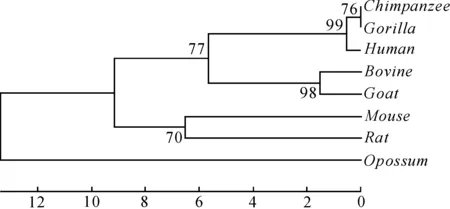
(a) 标准Bootstrap方法

(b) Subset Bootstrap方法

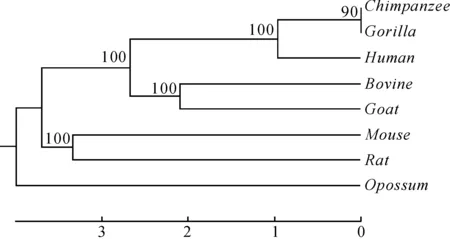
(c) 本文方法图2 3种不同方法对8个物种的聚类可靠性结果

(a) 标准Bootstrap方法

(b) Subset Bootstrap方法

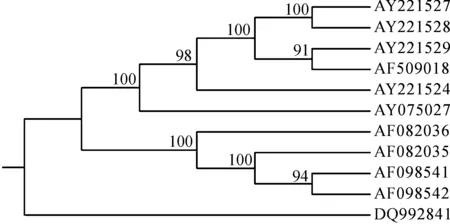
(c) 本文方法图3 3种不同方法对11个H5N1病毒的HA基因序列的聚类可靠性结果

图4 对29个H5N2病毒的HA基因序列使用本文方法得到的聚类可靠性结果

方法可靠性平均值实验数据1实验数据2实验数据3本文方法98.00097.87597.769SubsetBootstrap93.00094.75095.885标准Bootstrap84.00090.75093.231

3 结 语

本文首先利用多序列比对方法分析DNA序列之间的相似性，并构造相似距离矩阵；然后在相似距离矩阵基础上用UPGMA进行聚类，同时构建进化树显示聚类结果；最后使用基于遗传算法的改进评估方法对聚类结果进行可靠性分析。本文对给出的3组DNA数据用相同聚类方法构建进化树，并用标准Bootstrap、Subset-Bootstrap和本文方法对每组数据构建的进化树进行了可靠性评估。实验结果表明，本文提出的方法优于标准Bootstrap方法和Subset-Bootstrap方法。

[1] BLACKBURNE B P, WHELAN S. Class of multiple sequence alignment algorithm affects genomic analysis[J]. Molecular Biology and Evolution, 2013, 30(3): 642-653.

[2] VIJAYAKUMAR S, BHARGAVI A, PRASEEDA U, et al. Optimizing sequence alignment in cloud using hadoop and mpp database[C]//Cloud Computing (CLOUD), 2012 IEEE 5th International Conference on. IEEE, 2012: 819-827.

[3] KEMENA C, NOTREDAME C. Upcoming challenges for multiple sequence alignment methods in the high-throughput era[J]. Bioinformatics, 2009, 25(19): 2455-2465.

[4] JAIN A K, MURTY M N, FLYNN P J. Data clustering: a review[J]. ACM Computing Surveys (CSUR), 1999, 31(3): 264-323.

[5] CILIBRASI R L, VITáNYI P M B. A fast quartet tree heuristic for hierarchical clustering[J]. Pattern Recognition, 2011, 44(3): 662-677.

[6] ZHANG S, LI Z, BELAND K, et al. Model-based clustering with certainty estimation: implication for clade assignment of influenza viruses[J]. BMC Bioinformatics, 2016, 17(1): 287-296.

[7] FELSENSTEIN J. Confidence limits on phylogenies: an approach using the bootstrap[J]. Evolution, 1985,39(4): 783-791.

[8] EFRON B, HALLORAN E, HOLMES S. Bootstrap confidence levels for phylogenetic trees[J]. Proceedings of the National Academy of Sciences, 1996, 93(23): 13429-13429.

[9] TEKLEWOLD A, BECKER H C. Geographic pattern of genetic diversity among 43 Ethiopian mustard (Brassica carinata A. Braun) accessions as revealed by RAPD analysis[J]. Genetic Resources and Crop Evolution, 2006, 53(6): 1173-1185.

[10] KREISS J P, PAPARODITIS E. Bootstrap methods for dependent data: A review[J]. Journal of the Korean Statistical Society, 2011, 40(4): 357-378.

[11] APOSTOLICO A, GIANCARLO R. Sequence alignment in molecular biology[J]. Journal of Computational Biology, 1998, 5(2): 173-196.

[12] WANG Y, LI K B. An adaptive and iterative algorithm for refining multiple sequence alignment[J]. Computational Biology and Chemistry, 2004, 28(2): 141-148.

[13] GOTOH O. Significant improvement in accuracy of multiple protein sequence alignments by iterative refinement as assessed by reference to structural alignments[J]. Journal of Molecular Biology, 1996, 264(4): 823-838.

[14] KROGH A, BROWN M, MIAN I S, et al. Hidden Markov models in computational biology: Applications to protein modeling[J]. Journal of Molecular Biology, 1994, 235(5): 1501-1531.

[15] HOSEINI P, SHAYESTEH M G. Efficient contrast enhancement of images using hybrid ant colony optimisation, genetic algorithm, and simulated annealing[J]. Digital Signal Processing, 2013, 23(3): 879-893.

[16] KAIWARTYA O, PRAKASH S, SAHU D P, et al. Multiple sequence alignment using genetic algorithm and non-dominant sorting genetic algorithm-ii (nsga ii) and variants[J]. Journal of Bioinformatics and Intelligent Control, 2014, 3(4): 294-299.

[17] NOTREDAME C. Recent progress in multiple sequence alignment: a survey[J]. Pharmacogenomics, 2002, 3(1): 131-144.

[18] NOTREDAME C, HIGGINS D G, HERINGA J. T-Coffee: A novel method for fast and accurate multiple sequence alignment[J]. Journal of Molecular Biology, 2000, 302(1): 205-217.

[19] CHAICHOOMPU K, KITTITORNKUN S. Multithreaded ClustalW with improved optimization for intel multi-core processor[C]// International Symposium on Communications and Information Technologies. IEEE, 2006:590-594.

[20] HALL P, JING B. On sample reuse methods for dependent data[J]. Journal of the Royal Statistical Society. Series B (Methodological), 1996,58(4): 727-737.

(责任编辑： 康 锋)

Reliability Evaluation of DNA Sequence Clustering Based on Genetic Algorithm

SUNJie,LIZhong

(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018 , China)

Cluster analysis is a commonly used method for molecular biologists to infer the evolutionary relationship of homologous sequences. Evaluating the reliability of clustering is an important part of cluster analysis. Bootstrap is a statistical method for evaluating the reliability of clustering, which replaces all the nucleotide bases of DNA sequences for sampling analysis. On the basis of Bootstrap method, an improved method to evaluate the reliability of DNA sequence clustering is proposed. The method first randomly extracts a certain proportion of nucleotide bases from the original DNA sequence, and then uses the genetic algorithm to replace each of the extracted bases. The proposed method takes into account of the correlation between the bases, and the samples obtained are closer to the original sequence and more in line with the results of biological evolution. The method was used to evaluate the reliability of the phylogenetic tree constructed by DNA sequence clustering. The experimental results show that the accuracy of reliability assessment is improved, indicating that the method is feasible and effective.

DNA sequence; cluster analysis; phylogenetic tree; Bootstrap; reliability

10.3969/j.issn.1673-3851.2017.05.024

2016-11-11 网络出版日期： 2017-04-25

国家自然科学基金项目(11671009)；浙江省自然科学基金项目(LY14A010032)

孙 杰(1987-)，男，河南淮阳人，硕士研究生，主要从事计算机图形、生物信息可视化方面的研究。

李 重，E-mail：lizhong@zstu.edu.cn

O29

A

1673- 3851 (2017) 03- 0461- 06