高速射弹入水时空气携带量的数值模拟

朱棒棒，施红辉，侯 健，魏 平

(1.浙江理工大学机械与自动控制学院，杭州 310018；2. 海军工程大学兵器工程系，武汉 430033)



高速射弹入水时空气携带量的数值模拟

朱棒棒1，施红辉1，侯 健2，魏 平2

(1.浙江理工大学机械与自动控制学院，杭州 310018；2. 海军工程大学兵器工程系，武汉 430033)

使用Fluent 14.0 软件并选择VOF多相流模型，模拟了高速射弹入水过程。以直径为6.0 mm、长径比为12.0的圆柱体为射弹模型，分别计算了平头、圆头和尖头圆柱体射弹以100.0 m/s速度入水的超空泡流场。将入水超空泡形状的模拟计算结果，与Logvinovich半经验公式的计算结果进行对比发现：前半部分的空泡形状相互吻合，但后部空泡形状尺寸大于半经验公式的计算结果，这可能是因为入水空泡会夹带空气进入的缘故。另外对3种头型射弹的超空泡的相图作了对比分析,研究发现：尖头射弹产生的超空泡中夹杂的空气量最多，而平头射弹次之，圆头射弹最少；圆头射弹产生的超空泡中夹杂的空气体积分数最大，而尖头射弹次之，平头射弹最小。针对圆头圆柱体射弹，还计算了500.0、900.0 m/s和1500.0 m/s入水速度下的超空泡流场，并进行了相关对比分析。

超空泡；射弹；入水；夹杂空气量；空气体积分数；数值模拟

0 引 言

当水下航行体高速运动时，其周围压力会急剧降低，当压力低于水的饱和蒸气压时，液态的水就会汽化形成水蒸气，然后包裹整个航行体，这种现象称为超空泡现象[1]。这样会大幅度地降低航行体的阻力，使航行体在水下高速运动成为可能。

Savchenko 等[2]研究了人工通气空泡和超空泡闭合的特征，对超空泡的发展作了分析。Aristoff等[3]通过对疏水小球的研究，揭示了空泡形状与无量纲参数之间的关系。Yamashita等[4]在日本东北大学激波研究中心进行了水下超空泡射弹实验，可视化观察分析了球体和细长体以1.5～2.0 km/s的速度射进水中的情况。Klomfass等[5]提出了一种适用于水下超声速物体、可压缩超空泡流动细节分析的物理模型和数值分析方法。曹伟等[6]通过高速射弹实验研究了自然超空泡的形态特性和发展规律，证实了自然超空泡的直径和长度都随空化数的增大而呈指数规律减小。王海斌等[7]在水洞中开展了水下航行体通气超空泡的实验研究，结果表明：当来流速度不变时，超空泡的长度随通气率的增加而增加，阻力系数随空泡长度的增加先递增后递减；空化器直径对阻力系数有较大的影响，在弗劳德数较大的条件下，因空化器直径过大而出现阻力系数随通气量的增加而变大的趋势。陈晨等[8]采用VOF均质多相流模型对锥头圆柱体高速入水过程进行了数值模拟，对不同空气域压力条件入水过程的分析结果表明：空气域压力对自由液面上方的喷溅形态、空泡内部空化效应以及空泡表面闭合时间影响较大；空泡发生表面闭合的时间越早，空泡内部空化效应越强；空气域压力越大，空泡敞开阶段的空泡处半径越小。施红辉等[1,9-11]通过对高速物体出入水超空泡流动的大量实验，研究了水平入水、竖直出入水、倾斜入水以及不同长径比和头型的弹体的入水等情况。

目前，关于射弹入水时超空泡内空气携带量的定量研究不足，因为这涉及到如何建立空泡内的气体状态方程[12]，而关于射弹头型和入水速度对空气携带量的影响的研究更少。本文通过数值模拟，对高速射弹入水时空气携带量进行了研究。

1 模拟方法

1.1 控制方程

基本控制方程包括[1,10]：连续方程、动量方程；多相流模型采用VOF模型，湍流模型采用标准k-ε湍流模型，设置水、水蒸气、空气三相；空化模型采用Schnerr-Sauer模型。

连续方程为：

(1)

动量方程为：

其中：μ为混合物的动力粘度；ρ为混合物的密度；SM为自定义源；ui为混合物的速度。

标准k-ε湍流模型基本形式为：

其中：Gb为因浮力引起的湍流动能，Gk为因速度梯度引起的湍流动能，YM为可压缩湍流脉动膨胀总体耗散率；

(5)

C1ε、C2ε、C3ε、Cμ为常数，模型常数C1ε=1.44，C2ε=1.92，C3ε取水平方向速度μ与竖直方向速度ν比值的正切值；Cμ=0.09；σk和σε为k和ε的普朗特数，模型常数σk=1.0，σε=1.3.

(6)

Schnerr-Sauer空化模型水蒸气传输方程为：

(7)

1.2 数值模拟方法

计算模型采用直径均为6.0mm、长度均为72.0mm的平头、尖头和圆头圆柱弹体，其中：尖头圆柱弹体锥角为90.0°，圆头圆柱弹体头部为半球形。计算模型如图1所示。

图1 计算模型示意图

由于弹体轴线截面处空泡轮廓可以描述空泡形态，因此采用二维计算，整个计算区域是一个40.0mm×2200.0mm的长方形(如图2所示)。圆柱弹体距离上部压力入口边界距离为200.0mm，距离水面距离为10.0mm，水深1918.0mm。下部出口流设为压力出口，两侧设为固壁，压力出、入口对应压力均为标准大气压，对不同头型圆柱弹体进行数值模拟研究。

网格划分和初始相图如图3、图4所示。网格采用四边形结构化网格，在圆柱体射弹四周进行网格加密，平头、尖头和圆头计算区域网格单元数分别为497200.0、496744.0、497200.0。密度和动量采用二阶迎风格式，压力和速度耦合采用SIMPLE算法。采用VOF多相流模型，体积分数的离散采用Geo-Reconstruct格式。采用动网格技术进行数值模拟。空化现象包含了水、水蒸气和空气三种介质，图4显示了初始时刻三种介质的分布，灰色代表了空气相，黑色代表了水相，初始时刻并未发生空化现象，因此并没有水蒸气产生。在数值模拟中认为流动非定常，相互之间的转化采用空化模型。

图2 计算区域示意图

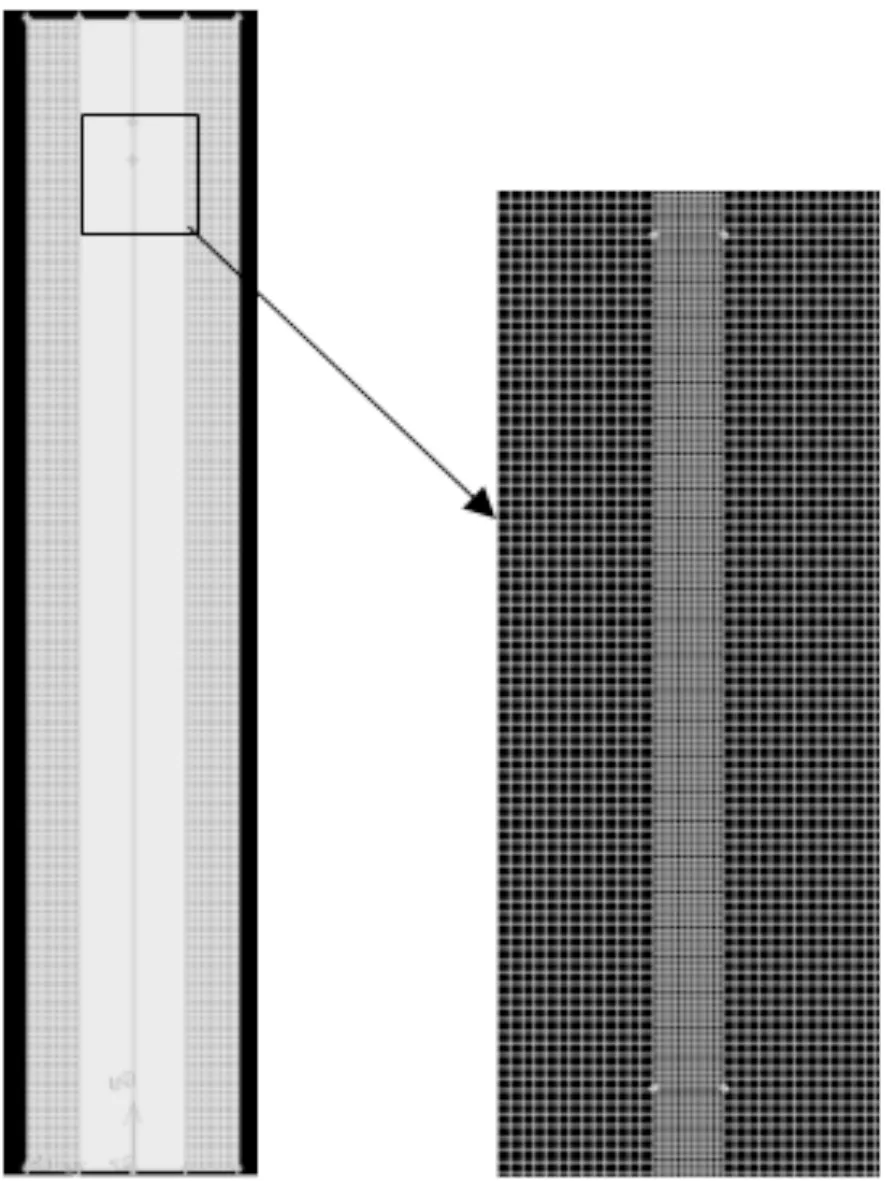
图3 计算区域和弹体网格周围划分

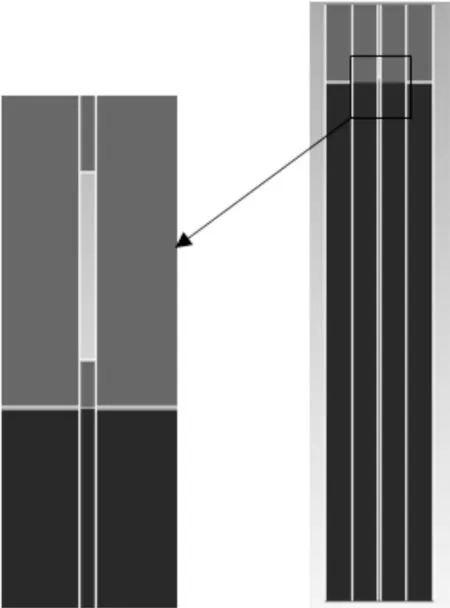
图4 弹体周围和计算区域初始相图

2 数值模拟结果与分析

2.1 弹体入水过程数值模拟与Logvinovich半经验公式对比

首先，本文对初速度为100.0m/s的不同头型圆柱弹体入水时，其头部与自由液面相互作用进行数值模拟。

当空泡尾部开口直径小于6.0mm时，本文设定空泡为接近闭合。图5为初速度为100.0m/s平头圆柱弹体入水过程数值模拟的液相图，图中黑色代表气相，灰色代表水。图5 (1)-(3) 中，弹体向下运动还未与自由液面接触，自由液面处于平静状态；图5(4)中，平头圆柱弹体开始与自由液面接触，发生相互作用挤压自由液面，自由液面开始略微凹陷，并在平头圆柱弹体头部开始有空泡形成；图5(5)-(15)中，平头圆柱弹体逐渐入水，空泡逐渐增大，慢慢包裹弹体，直至图5(15)弹体全部浸入水中并全部被空泡包裹；图5(16)-(27)中，随着弹体继续运行，空泡继续增大，直至图5(27)整个空泡接近闭合。图5(1)时刻为50.0μs，图5(1)-(20)相邻图片之间的时间间隔为50.0μs，图5(21)时刻为1.5ms，图5(21)-(26)相邻图片之间的时间间隔为0.5ms，图5(27)时刻为5.5ms，图5(28)时刻为6.0ms。

图5 初速度为100.0 m/s平头圆柱弹体入水过程数值模拟液相图

图6和图7分别为初速度为100.0m/s尖头和圆头圆柱弹体入水过程数值模拟液相图。它们与平头圆柱弹体入水过程相似。图6(1)时刻为50.0μs，图6(1)-(20)相邻图片之间的时间间隔为50.0μs，图6(21)时刻为1.5ms，图6(21)-(26)相邻图片之间的时间间隔为0.5ms，图6(27)时刻为5.0ms，图6(28)时刻为6.0ms。图7(1)时刻为50μs，图7(1)-(20)相邻图片之间的时间间隔为50.0μs，图7(21)时刻为1.5ms，图7(21)-(26)相邻图片之间的时间间隔为0.5ms，图7(27)时刻为4.7ms，图7(28)时刻为6.0ms。

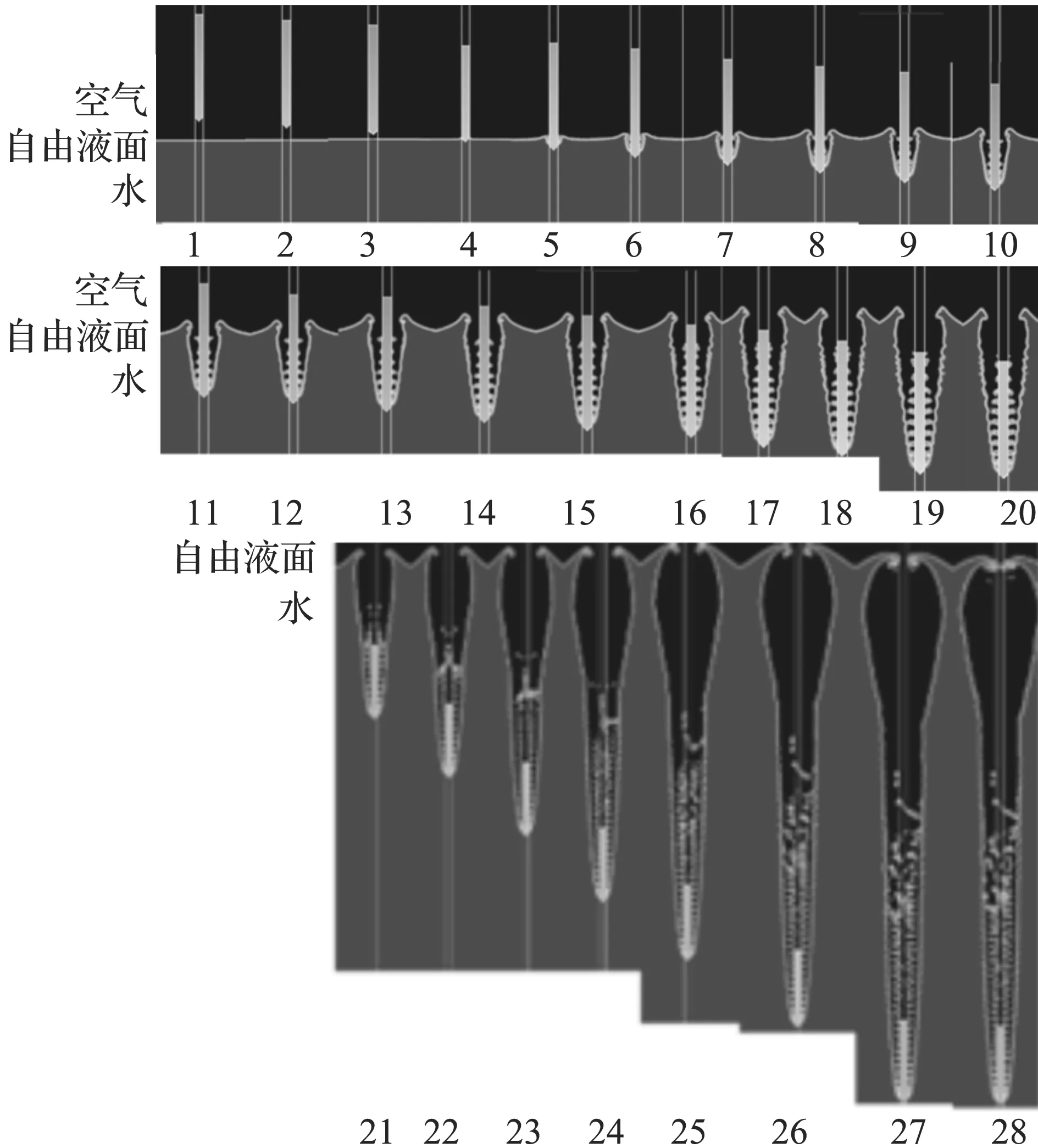
图6 初速度为100.0 m/s尖头圆柱弹体入水过程数值模拟液相图

通过对比以上三种头型的弹体空泡的形成过程，可发现头型对空泡形态特性影响显著。从尾部来看，平头圆柱弹体形成空泡在5.5ms后接近闭合，尖头圆柱弹体和圆头圆柱弹体形成空泡分别在5.0ms和4.7ms后接近闭合。图8为空泡接近闭合后，三种头型空泡形态与Logvinovich半经验公式的对比。X为空泡轴向距离，Y为空泡纵向距离。从图8中可以看出，在空泡前部区域，三种头型形成的超空泡与Logvinovich半经验公式空泡形态比较吻合，这是因为在空泡前部区域弹体被水蒸气包裹，未受空气夹杂的影响，同时说明本文数值模拟方法正确。而在尾部区域，三种头型形成的空泡均与Logvinovich半经验公式空泡形态偏离较大，这是因为在尾部区域空泡受夹杂的空气影响，使空泡尾部区域空泡体积偏大，而不同头型射弹的尾部区域空泡形态之间差别较大。

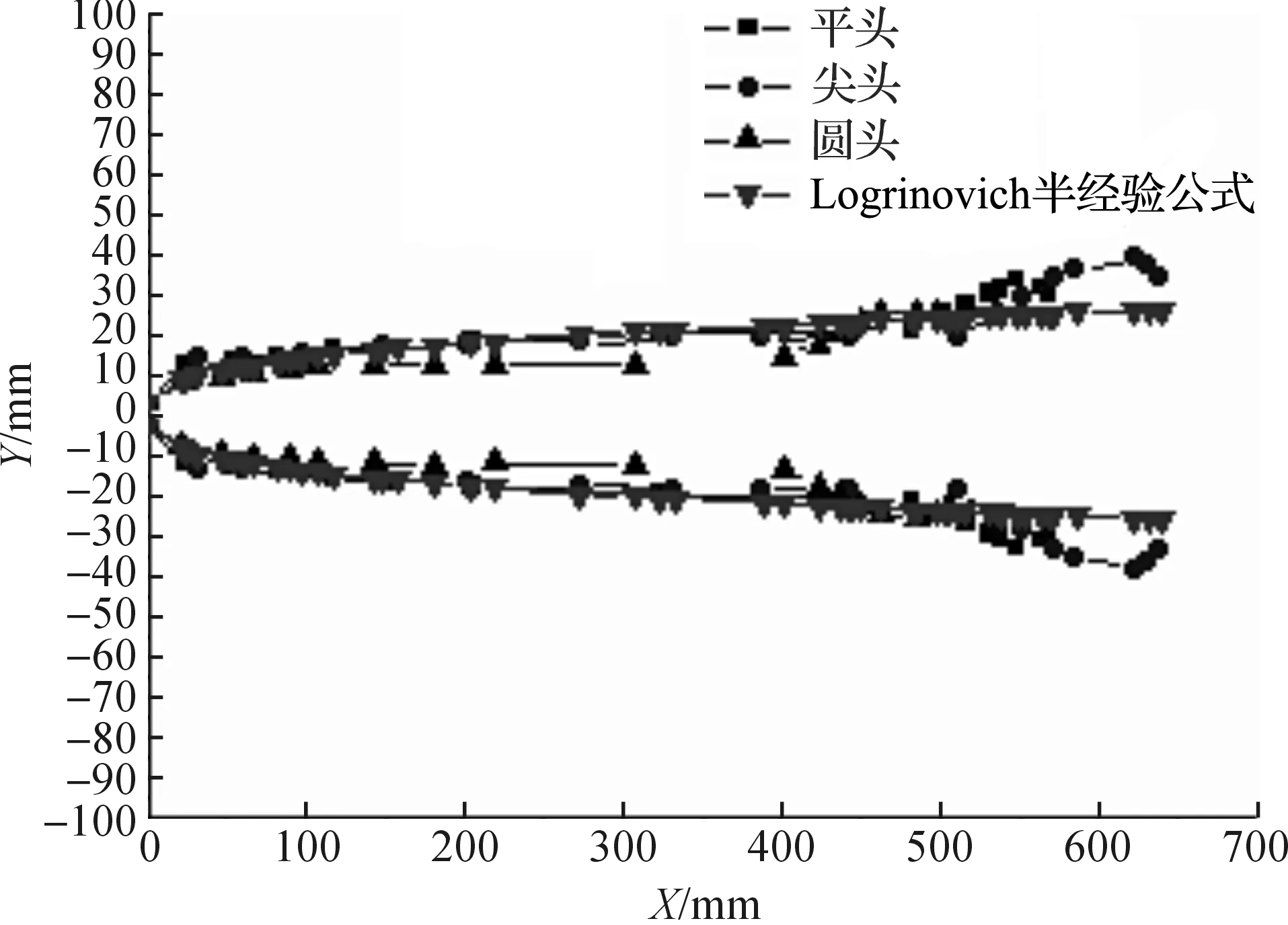
图8 三种头型与Logvinovich半经验公式空泡形态对比

2.2 弹体头型对空泡中空气携带量的影响

从图8可知头型对空泡尾部区域夹杂的空气有明显影响。因此本文对不同头型形成空泡中夹杂的空气进行定量的测量。图9中从左至右依次为平头、尖头和圆头三种头型圆柱弹体在6.0 ms时刻形成的非凝结性气体空气相的分布，深灰色为空气相，亮灰色为水蒸气相，黑色为水相。

将图9中的图片分别导入CAD，进行空泡面积的测量以及空泡中空气相面积(二维超空泡)的测量，测量结果见图10。

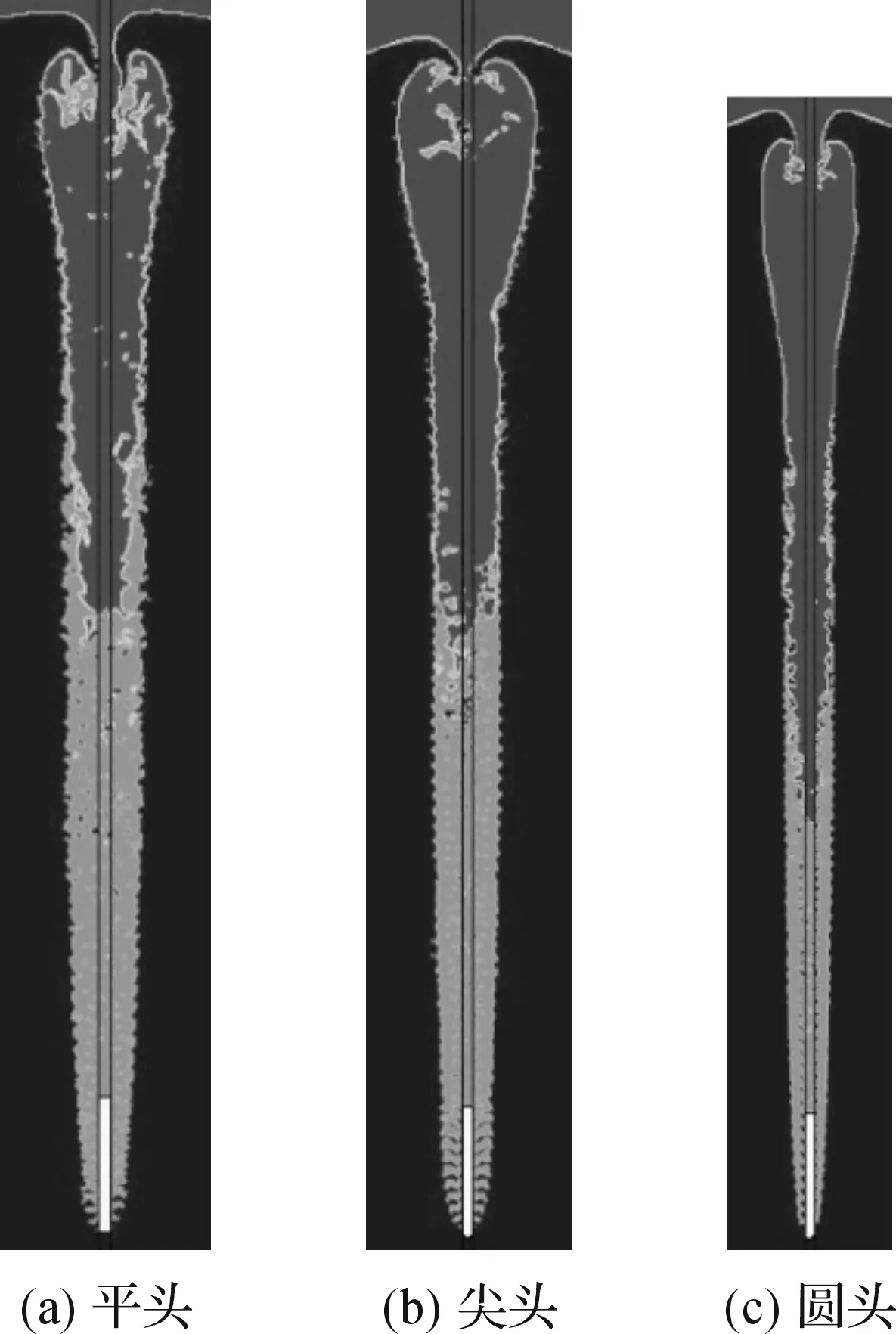
图9 6.0 ms时三种头型圆柱弹体形成空泡相的分布

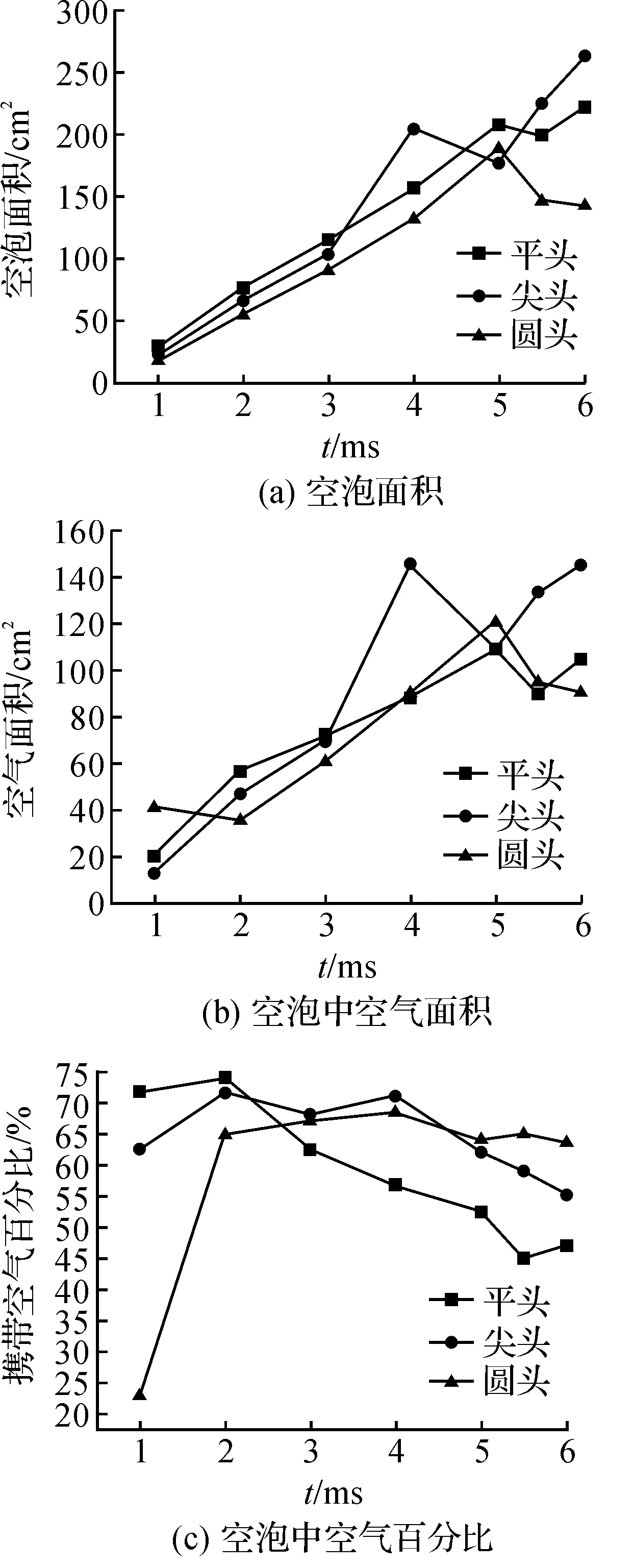
图10 三种头型弹体形成空泡面积、空泡中空气面积以及空泡中空气百分比随时间的变化

从图10(a)中可以看出在3.0 ms之前平头弹体产生空泡体积大于尖头大于圆头；3.0～4.0 ms尖头弹体产生空泡迅速增大，此时尖头弹体产生空泡大于平头大于圆头；在5.0 ms附近尖头弹体产生空泡有一个收缩的过程，而平头和圆头弹体产生空泡在5.5 ms附近有个收缩的过程；最后在6.0 ms空泡几乎完全闭合时尖头形成空泡大于平头大于圆头。从图10(b)中可以看出空泡中空气的变化与图10(a)中对应头型产生空泡的变化高度一致。从图10(c)可以看出，在起始阶段平头和尖头弹体产生空泡中空气的体积分数较高，接下来持续减小；圆头弹体产生空泡中空气的体积分数在起始阶段较低，接下来持续增加，在6.0 ms空泡几乎完全闭合时，空泡中空气的体积分数，圆头的大于尖头大于平头。

2.3 弹体入水速度变化对空泡形状及空气携带量的影响

图11从左至右依次为圆头100.0、500.0、900.0、1500.0 m/s初速圆柱弹体形成空泡的相分布图，分别将其导入CAD进行空泡轮廓和空气携带量(图中黑色部分)的测量，结果见图12和图13。从图12可以看出，弹体速度从100.0、500.0、900.0 m/s所形成的空泡尺寸大小依次递增，当弹体速度增至1500.0 m/s时，所形成空泡尺寸反而减小，其大小介于100.0 m/s和500.0 m/s弹体所形成空泡之间。这可能由于该速度跨水声速，水的可压缩性开始影响空泡形状的缘故。

图11 深度为0.6 m时不同速度入水空泡的相分布

图12 速度变化对空泡轮廓的影响(圆头弹体)

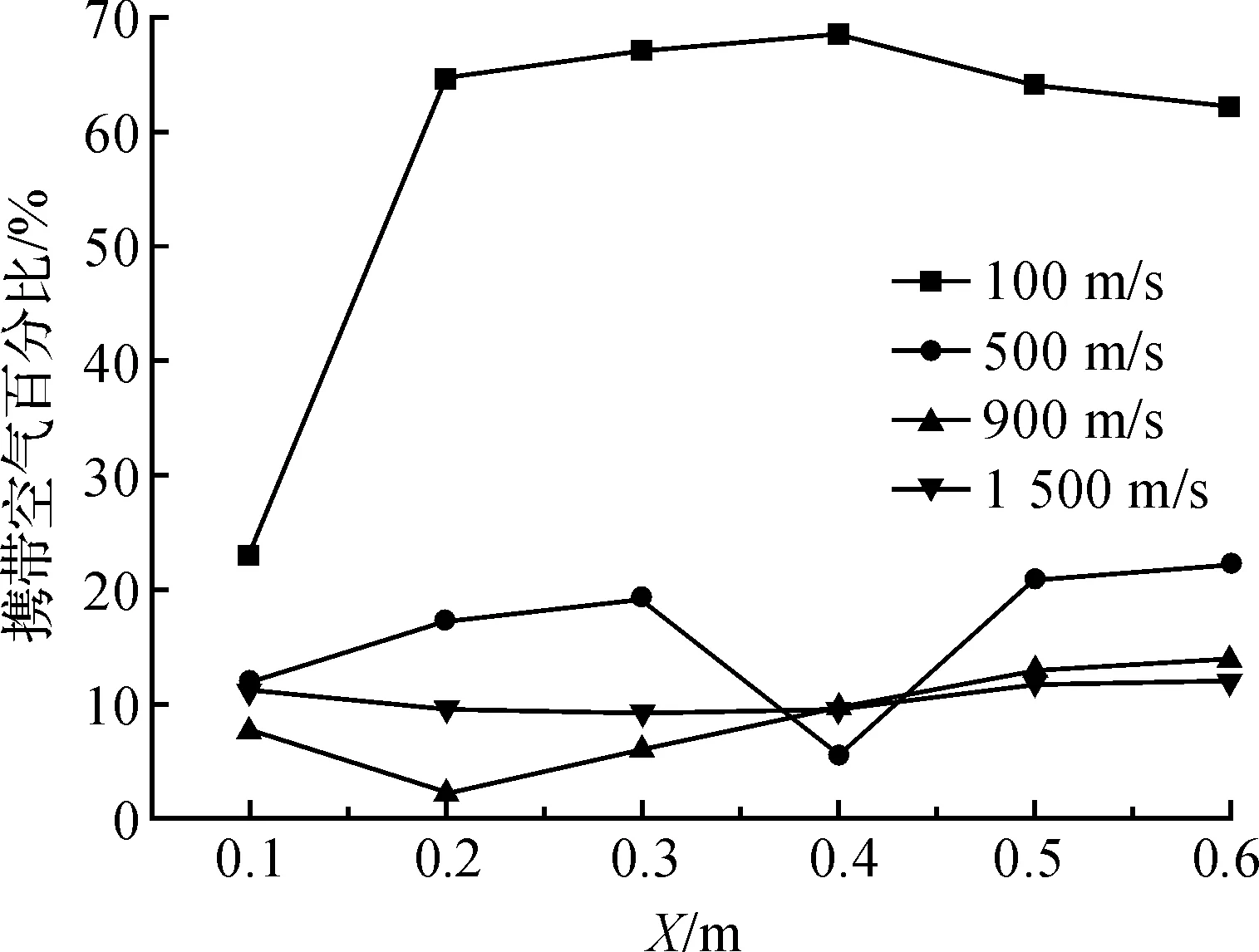
图13 速度变化对携带空气百分比的影响(圆头弹体)

图13中横坐标为入水深度，纵坐标为携带空气百分比。从图中可以看出在入水前期(深度小于0.5 m) 4种速度形成的空泡中空气的百分比变化明显，特别是速度为100.0 m/s时前期变化更为剧烈。当深度大于0.5 m时空气百分比趋于稳定，并且100.0 m/s速度弹体形成空泡空气百分比大于500.0 m/s大于900.0 m/s大于1500.0 m/s速度弹体形成空泡空气百分比。

3 结 论

a) 尖头圆柱弹体产生空泡体积最大，平头圆柱弹体次之，圆头圆柱弹体最小；圆头圆柱弹体产生空泡接近闭合时间最短，尖头圆柱弹体次之，平头圆柱弹体最长。

b) 尖头圆柱弹体产生空泡携带的空气量最多，平头圆柱弹体次之，圆头圆柱弹体最少。然而，从占空泡总体积的百分比来衡量，圆头圆柱弹体产生空泡夹杂的空气百分比最大，尖头圆柱弹体次之，平头圆柱弹体最小。

c) 在速度为100.0、500.0、900.0 m/s圆头圆柱弹体入水过程中，其形成空泡尺寸依次增大，1500m/s弹体形成空泡尺寸反而减小；100.0、500.0、900.0、1500.0 m/s圆柱弹体入水形成空泡中携带空气百分比在前期有所变化，后期平稳后空气百分比依次递减。

[1] 施红辉,周杨洁,彭立兵,等.伴随空化现象的细长体倾斜穿透水体过程研究[J].浙江理工大学学报,2016,35(3):392-397.

[2] SAVCHENKO Y. Supercavitation: problems and perspectives[C/OL]//CAV 2001: Fourth International Symposium on Cavitation. California Institute of Technology. Pasadena, USA. 2001. http://caltechconf.library. caltech.edu/66/1/Savchenko.pdf.

[3] ARISTOFF J M, BUSH J W M. Water entry of small hydrophobic spheres[J]. Journal of Fluid Mechanics,2008,619:45-78.

[4] YAMASHITA S, TOGAMI K, SAEKI T, et al. Study of a hypervelocity underwater projectile[C]//Proceedings of the 24th International Symposium on Shock Waves Beijing, China.2004:1303-1308.

[5] KLOMFASS A, SAKL M. Numerical analysis of the supercavitating supersonic flow about blunt bodies[C]//25th International Symposium on Shock Waves, Bangalore, India.2005:17-22.

[6] 曹伟,王聪,魏英杰,等.自然超空泡形态特性的射弹实验研究[J].工程力学，2006,23(2):75-179.

[7] 王海斌,张嘉钟,魏英杰,等.水下航行体通气超空泡减阻特性实验研究[J].船舶工程，2006,28(3):14-17.

[8] 陈晨,马庆鹏,魏英杰,等.空气域压力对高速射弹入水流场影响[J].北京航空航天大学学报，2015，41(8):1443-1450.

[9] 施红辉,罗喜胜.可压缩性和高速多相流动[M].合肥：中国科学技术大学出版社，2014：156-238.

[10] 周素云,施红辉,胡青青,等.水平超空泡发生装置的研制及相关实验研究[J].浙江理工大学学报,2013,30(2):218-223.

[11] 施红辉,吴岩,周浩磊,等.物体高速出水实验装置研制及流场可视化[J].浙江理工大学学报,2011,28(4):534-539.

[12] NEAVES M D, EDWARDS J R. All-speed time-accurate underwater projectile calculations using a preconditioning algorithm[J]. Fluids Engineering,2006,128(2):284-296.

(责任编辑： 康 锋)

Numerical Simulation of Air Entrainment Amount During High-Speed Projectile into Water

ZHUBangbang1,SHIHonghui1,HOUJian2,WEIPing2

(1.Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China；2. Department of Ordnance Engineering, Naval University of Engineering, Wuhan 430033, China)

The Fluent 14.0 software and the VOF multiphase flow model are used to simulate the process of high-speed projectile into water. The cylinder with the diameter of 6.0mm and length-diameter ratio of 12.0 is used as the projectile model. The projectiles with a flat head, conical head and spherical head respectively produce supercavitating flows in water at a speed of 100.0 m/s. By comparing the analog computation result of supercavity shape with the result of Logvinovich’s semi-empirical formulas, it is found that the supercavity shape in the front half coincides with each other, but supercavity shape size in the back half is bigger than the calculation result of semi-rational formula. This may be because of the air entrainment. In addition, the phase diagram of the three kinds of head shape supercavitation projectiles are compared and analyzed. It is found that the air entrainment amount of the conical head cylinder is the most, followed by the flat head cylinder and the spherical head cylinder respectively. The air entrainment volume fraction of the spherical head cylinder is the largest, followed by the conical head cylinder and the flat head cylinder respectively. For the projectile with spherical head, the flow fields at 500.0, 900.0 m/s and 1500.0 m/s entry speed are simulated and discussed. Besides, relevant contrastive analysis is conducted.

supercavitation; projectile; water entry; air entrainment amount; air volume fraction; numerical simulation

10.3969/j.issn.1673-3851.2017.05.016

2016-09-19 网络出版日期：2017-01-03

浙江省自然科学基金项目(LY16A020003)；“十三五”海军装备预研项目

朱棒棒(1990-)，男，安徽亳州人，硕士研究生，主要从事超空泡流动方面的研究。

施红辉，E-mail： hhshi@zstu.edu.cn

O352;O359

A

1673- 3851 (2017) 03- 0402- 07