基于纹理特征与广义相关性结构信息的医学图像融合

潘树伟，戴文战，李俊峰

(1.浙江理工大学自动化研究所，杭州 310012；2. 浙江工商大学信息与电子工程学院，杭州 310012)



基于纹理特征与广义相关性结构信息的医学图像融合

潘树伟1，戴文战2，李俊峰1

(1.浙江理工大学自动化研究所，杭州 310012；2. 浙江工商大学信息与电子工程学院，杭州 310012)

结合多尺度变换的图像特征，提出了一种基于纹理特征与相关性结构信息的医学图像融合方法。首先对已配准的源图像进行非下采样Contourlet变换，得到低频、高频子带系数。其次考虑人眼视觉对纹理特征的敏感性，提出局部差分计盒维数来统计图像的纹理信息；分析NSCT高频子带兄弟系数间及其父子系数间的强相关性，分别计算出系数间的结构相似度与邻域拉普拉斯能量和，作为高频子带系数间的广义相关性结构信息。然后对低频提出Sigmoid函数自适应融合，对高频采用广义相关性结构信息取大法。最后进行逆NSCT变换得到融合图像。通过灰度与彩色图像融合实验发现，该算法不仅可以保留源图像的边缘信息，还得到较好的客观评价指标和视觉效果。

医学图像融合；非下采样Contourlet变换；局部差分计盒维数；广义相关性结构信息

0 引 言

随着电子科学的发展，医学成像技术被广泛应用于临床诊断。不同形式的医学影像反映不同的人体器官和组织信息[1]。解剖图像(CT、MRI等)提供相对高分辨率的解剖信息和生理特征，而功能图像(SPECT、PET等)提供人体器官的新陈代谢和血液循环信息，但空间分辨率较低。单一模态的医学图像只提供片面、不完整的信息，因此，多模态医学图像融合具有很大的研究价值，不仅互补了医学图像信息，还有助于临床中对病灶的诊断[2-4]。

近年来，基于多尺度几何变换的多模态医学融合方法由于符合人类的视觉原理而越来越受人们的重视[5]。李俊峰等[6]提出了基于提升小波变换的医学图像融合方法，该方法对低频子带使用区域能量加权规则，在高频子带中，针对噪声含量的不同，对低层高频子带采用基于计盒分维法，对高层高频子带采用区域梯度能量加权融合规则。该方法虽然有效抑制了噪声干扰，但对于计盒分维只使用了全局分维数，没有考虑到单个像素点的分维数对图像纹理特征的作用。Yang等[7]提出基于二型模糊逻辑NSCT域的图像融合方法，该方法进一步给出了集合中隶属度值的模糊程度，增强了传统模糊描述和处理不确定性的能力，然而在隶属度函数的选择时比较复杂，计算量大、时间长。Srivastava等[8]提出基于本地能量Curvelet域的图像融合算法，但该算法只考虑了本地能量，没考虑人眼视觉对于纹理细节、轮廓信息的敏感度远大于像素强度本身的特点。Bhateja等[9]提出基于SWT与NSCT的融合方法，但其NSCT域使用取大法，容易受到噪声的干扰，且没有考虑到子带系数间的相关性，易造成部分信息的丢失。

基于上述分析，结合多尺度变换的图像特征，本文提出了一种基于纹理特征与相关性结构信息的医学图像融合方法。本文选取非下采样Contourlet变换(nonsubsampled contourlet transform, NSCT)作为多尺度变换工具，与小波变换相比，NSCT具有平移不变性和多方向性，能更好地捕捉图像中的奇异点，以最稀疏的方式表示图像的轮廓及边缘信息。局部差分计盒维数(local differential box counting, LDBC)能很好地表征图像的边缘轮廓信息及纹理信息。经NSCT分解后的高频子带兄弟间、父子间、邻域间存在着相关性，保留着基本轮廓结构信息，因此，本文计算出系数间的结构相似度(structural similarity, SSIM)与邻域拉普拉斯能量和，作为高频子带系数间的广义相关性结构信息(information of generalized correlation structure, IGCS)。最后对获得的融合系数进行逆NSCT变换得到融合图像。

1 NSCT子带系数间广义相关性结构信息

1.1 非下采样Contourlet变换(NSCT)

Cunha等[10]提出了NSCT方法，该变换方法没有对信号下采样，而是对滤波器进行上采样，从而使得其具有平移不变性，且继承了多尺度性、方向选择性。NSCT是由非下采样金字塔滤波器组(nonsubsampled pyramid filter bank, NSPFB)和非下采样方向滤波器组(nonsubsampled directional filter bank, NSDFB)两个独立步骤完成的。首先对图像进行多尺度分解，得到一个低频子带和多个尺度的高频子带系数，然后NSDFB对各尺度高频子带进行多方向、多分辨率分解，从而获得了各尺度方向各异的子带系数。在分解、重构过程中采用非下采样，使得分解得到的图像不存在频率混叠的现象。图1为NSCT变换的结构框图。图2为NSCT的理想区域划分图。

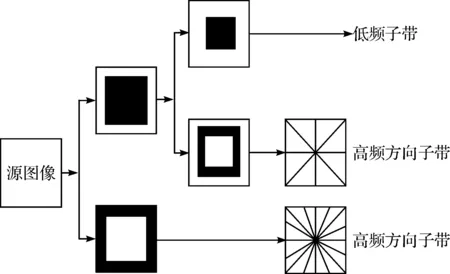
图1 NSCT变换结构框图

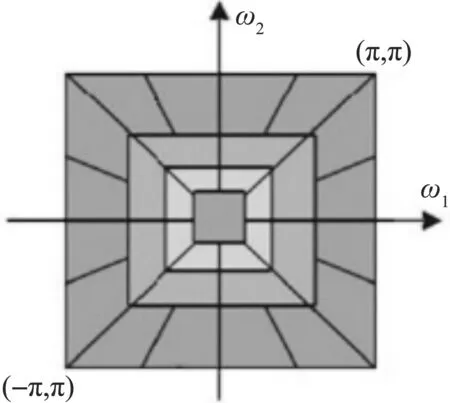
图2 NSCT理想频域划分

1.2 NSCT子带系数间的相关性

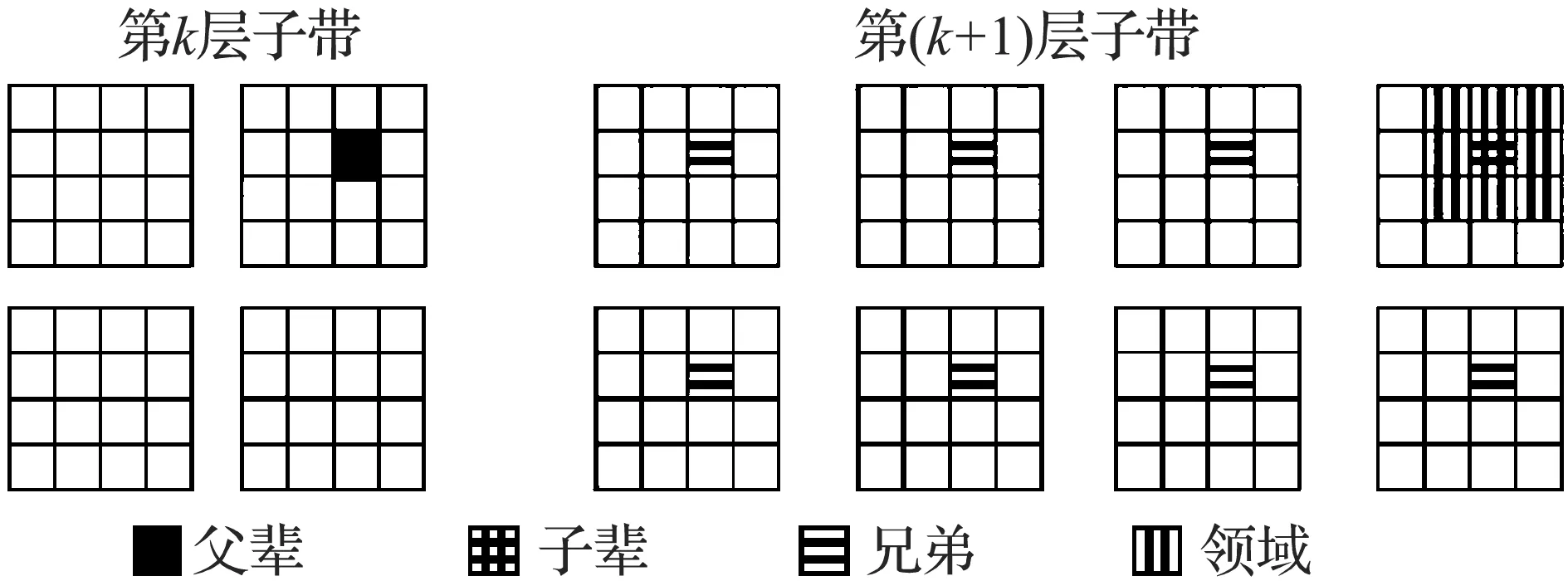
图3 NSCT系数间的关系

传统的多尺度几何算法都是假设尺度间是统计无关的，然而只对同一尺度、同一方向的系数进行融合规则的计算，导致尺度间强相关性细节信息的丢失[12]。本文选取自然图像cameraman(如图4(a)所示)进行实验，为计算方便，对其进行2层NSCT分解，尺度从粗到细依次为4、8个方向子带，图4(b)为最细尺度中的一个高频子带。每一个高频子带的NSCT系数都构成一个随机场，且各个系数具有独立的概率密度，因此对图4(b)进行概率分布统计，结果如图5所示。

图4 Cameraman图像及其NSCT分解图像

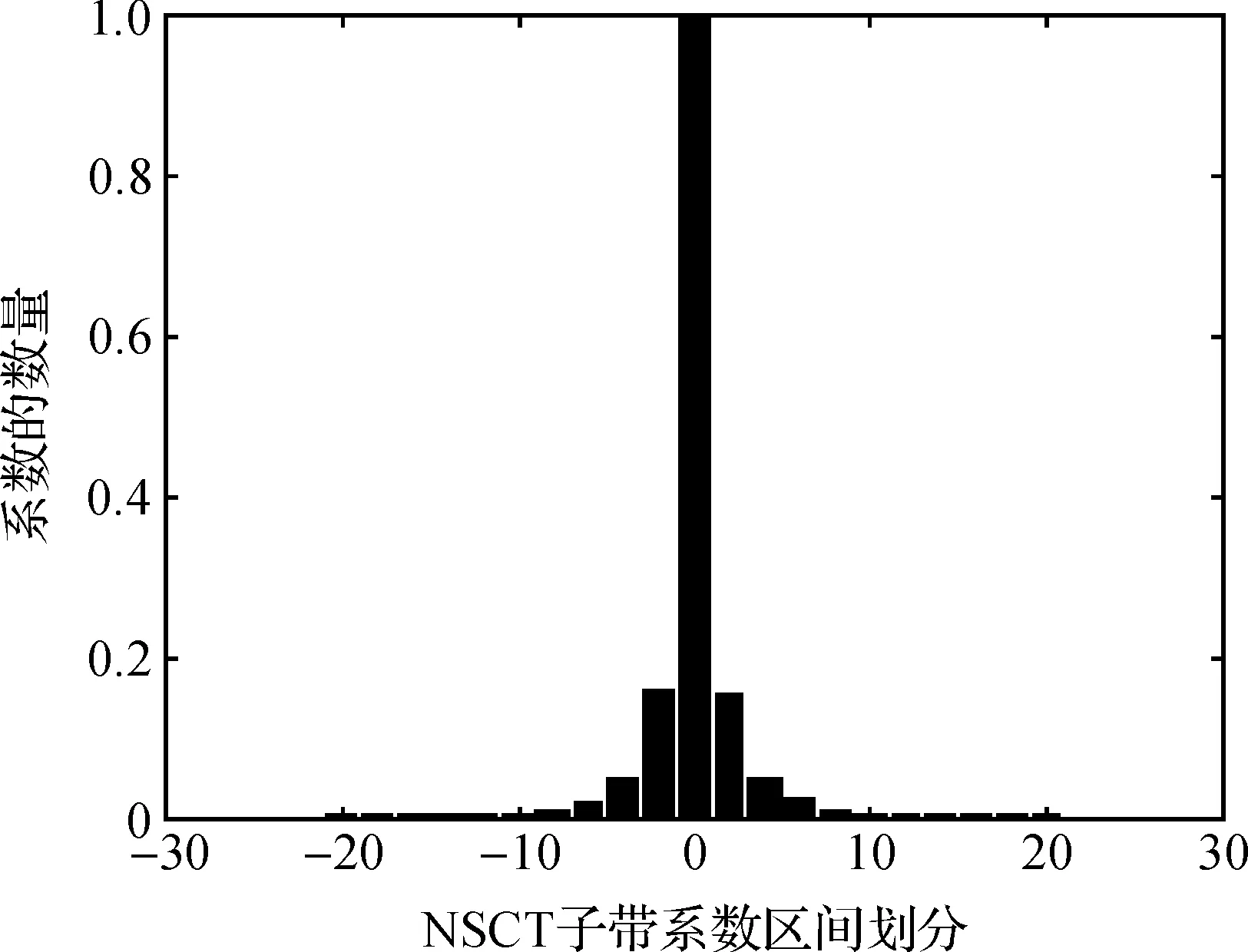
图5 图4(b)子带系数归一化直方图

分析图5可以看出，高频子带系数的分布基本对称，且呈现“高尖峰，长拖尾”的分布特性，即概率分布的均值为0。这表明，NSCT变换能稀疏地表示分解的轮廓段，其中幅值为0的系数占据了绝大部分，幅值较大的系数只有少数，且其表示图像中显著的细节特征。然而这种稀疏特性在多尺度和不同方向的子带系数上也普遍存在。由此可见，NSCT的子带系数与其邻域系数、兄弟系数及父系数间存在强相关性、持续性和聚集性。

1.3 广义相关性结构信息

图像中的结构特征具有重点突出性，有助于人类视觉系统在观察时分辨图像中的事物，而且在融合图像评价方法中，SSIM描述图像的结构相似度也用来评估图像的质量[13]。

SSIM包括图像亮度、图像对比度、图像结构比较，其表达式如下：

(1)

(2)

(3)

由式(4)得到像素点dk,l(i,j)兄弟子带间结构相似度为SSIM(dk,l,dk,lq)，其中：k为尺度层数，l为方向级数，q∈{1,2,…,l}。同理可得父子子带间结构相似度为SSIM(dk,l,dk-1,l)。那么可定义像素点dk,l(i,j)的相关性结构相似度：

然而，NSCT系数在一定程度上也依赖于邻域的特性，拉普拉斯能量和能很好地反应图像的边缘特征与能量特性。因此，结合相关性结构相似度与拉普拉斯能量和，定义广义相关性结构信息(IGCS)如下：

IGCSk,l(i,j)=RE[dk,l(i,j)]×NSMLk,l(i,j)

(6)

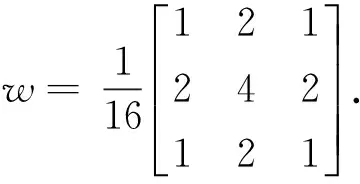
(8)

其中：dk,l(i,j)为NSCT分解后在k层尺度l级方向上位置为(i,j)的高频子带系数；MLk,l(i,j)为拉普拉斯能量；step表示系数间的可变间距，本文取1。

由此可见，IGCS不仅能突出NSCT图像中兄弟间、父子间系数的结构特征，反映其结构信息的退化程度，而且还具有邻域间边缘及能量的表达，捕获了图像中丰富的细节信息。

2 局部差分计盒维数

人类视觉在处理数量庞大的信息时，注意机制具有极其重要的作用，它能够将有限的资源优先分配给有用的信息，从而优先处理最有价值的数据[14]。然而人眼视觉对于图像纹理、轮廓特征比像素本身强度更加敏感，所以统计图像的纹理信息是提高图像融合质量的重要内容。

分形能提供自然图像复杂度信息，是一种最接近自然的算法，分维是分形的维数，它可以定量地刻画分形的特点，用以描述图像的特征[15-17]。LDBC利用图像分块处理的思想，能处理大数据图像信息，分形维数越小，对应的图像表面越光滑，分形维数越大，图像像素变化越剧烈，图像纹理表征越好。LDBC计算过程如下：

a)以像素点(x，y)为中心，取出T×T的窗口大小的图像。

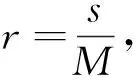
c)将图像视为三维空间中的曲面，x、y表示平面位置，z表示灰度值。每个子块上是一列s×s×s的盒子。在每个尺度r下，使得第(i，j)子块中的最小和最大灰度级分别落入第k和第l个盒子中，则覆盖该块的盒子的数目计算为：

nr(i,j)=l-k+1

(9)

d) 移动窗口，计算每个子块下的nr(i,j)，则覆盖整个图像所需的盒子数为：

(10)

e)对于不同的r所获得的n个点对{ log(1/r) ，log(Nr) }，用最小二乘法进行线性拟合，将这个直线斜率作为该点的局部计盒维数LDBC(i，j)。

3 图像融合算法

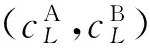
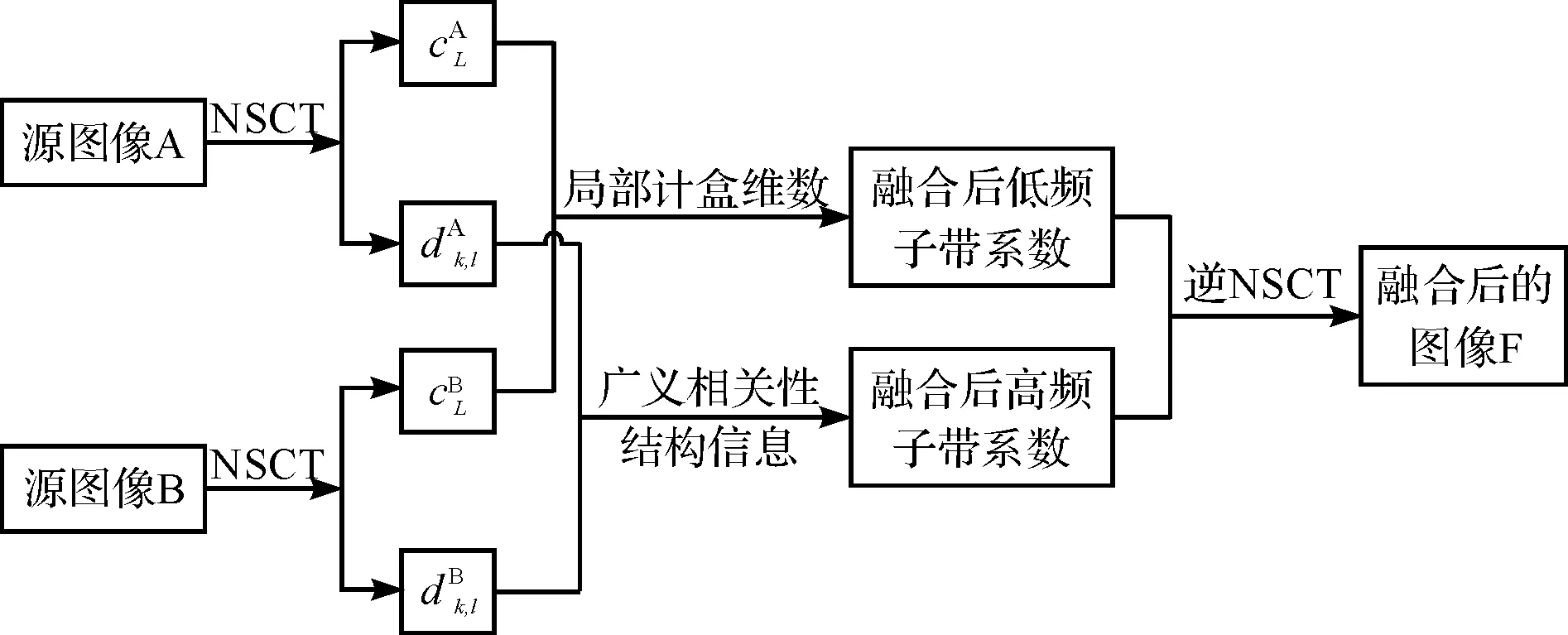
图6 基于纹理特征与广义相关性结构信息的医学图像融合

3.1 低频子带融合

图像经NSCT分解后，低频子带是源图像的近似部分，反映了源图像的概貌特征和主体轮廓。然而，加权平均准则、取系数极大值等，此类方法会使图像对比度减弱，造成图像信息的部分丢失，因此本文采用LDBC来统计图像的纹理信息，且符合人眼视觉特性，并提出Sigmoid函数自适应调节融合。步骤如下：

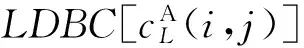
b)本文构造一个Sigmoid函数，表达式如下：

(11)

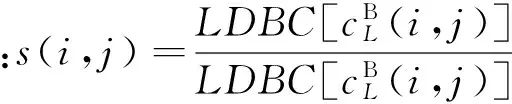
c)最终低频子带融合规则如下：

(12)

从式(12)可以得出，本文提出的融合规则可以根据图像各自的LDBC来动态的分配权值，因此达到自适应的融合效果。

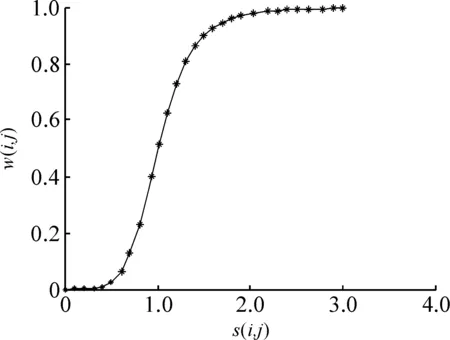
图7 Sigmoid函数

3.2 高频子带融合

高频子带中包含着图像的细节信息，模值越大表示图像变化越强烈。拉普拉斯能量和能捕捉图像的边缘特征和轮廓信息，在一定程度上表征图像的清晰度和聚焦特性。相关性结构相似度描述了图像的亮度、对比度及结构信息。所以广义相关性结构信息能很好地表达图像细节部分，改进图像的视觉效果。具体融合步骤如下：

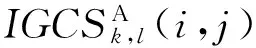
b)广义相关性结构信息采用取大规则计算：

(13)

4 实验结果及分析

4.1 灰度图像融合

为了验证本文所提算法的有效性，以灰度图像融合实验为例，与文献[6]、文献[8]、文献[9]、文献[18]、文献[19]、文献[20]、文献[21]进行实验对比。文献[6]提出了基于提升小波的图像融合算法，该算法根据噪声含量的不同，低频采用区域能量规则，高频采用基于分盒计数与区域梯度能量相结合的规则。文献[8]提出了Curvelet域的本地能量算法。文献[9]提出了基于SWT与NSCT的融合方法，该方法在SWT域采用主成分分析法，第二阶段采用NSCT域取大法。文献[18]提出了基于补偿机制的NSCT域图像融合算法。文献[19]根据高频子带的互信息大小，分别采用不同规则进行融合。文献[20]提出了基于提升小波和PCNN的融合算法。文献[21]采用在线字典训练和选择能量梯度差异程度大的融合规则。本文采用信息熵(IE)、边缘信息评价因子(QABF)、标准差(SD)和空间频率(SF)对融合图像进行定量分析。

图8(a)、8(b)为正常脑部CT/MRI医学图像。图9(a)、9(b)为多发性脑梗塞MR-T1/MR-T2医学图像。图10(a)、10(b)为急性脑卒中CT/MRI医学图像。图8(c)、9(c)、10(c)为文献[6]提出的融合算法结果图像。图8(d)、9(d)、10(d)为文献[8]提出的融合规则结果图像。图8(e)、9(e)、10(e)为文献[9]提出的融合算法结果图像。图8(f)、9(f)、10(f)为文献[18]提出的融合规则结果图像。图8(g)、9(g)、10(g) 为文献[19]提出的融合规则结果图像。图8(h)、9(h)、10(h) 为文献[20]提出的融合规则结果图像。图8(i)、9(i)、10(i) 为文献[21]提出的融合规则结果图像。图8(j)、9(j)、10(j)为本文提出的融合规则结果图像。表1—表3为不同源图像经多种融合算法处理后的图像质量评价结果。

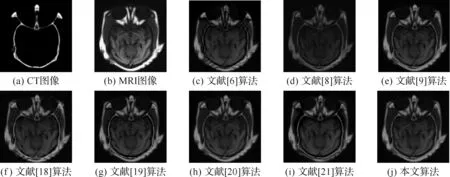
图8 正常脑部CT/MRI医学图像融合结果

图9 多发性脑梗塞MR-T1/MR-T2医学图像融合结果

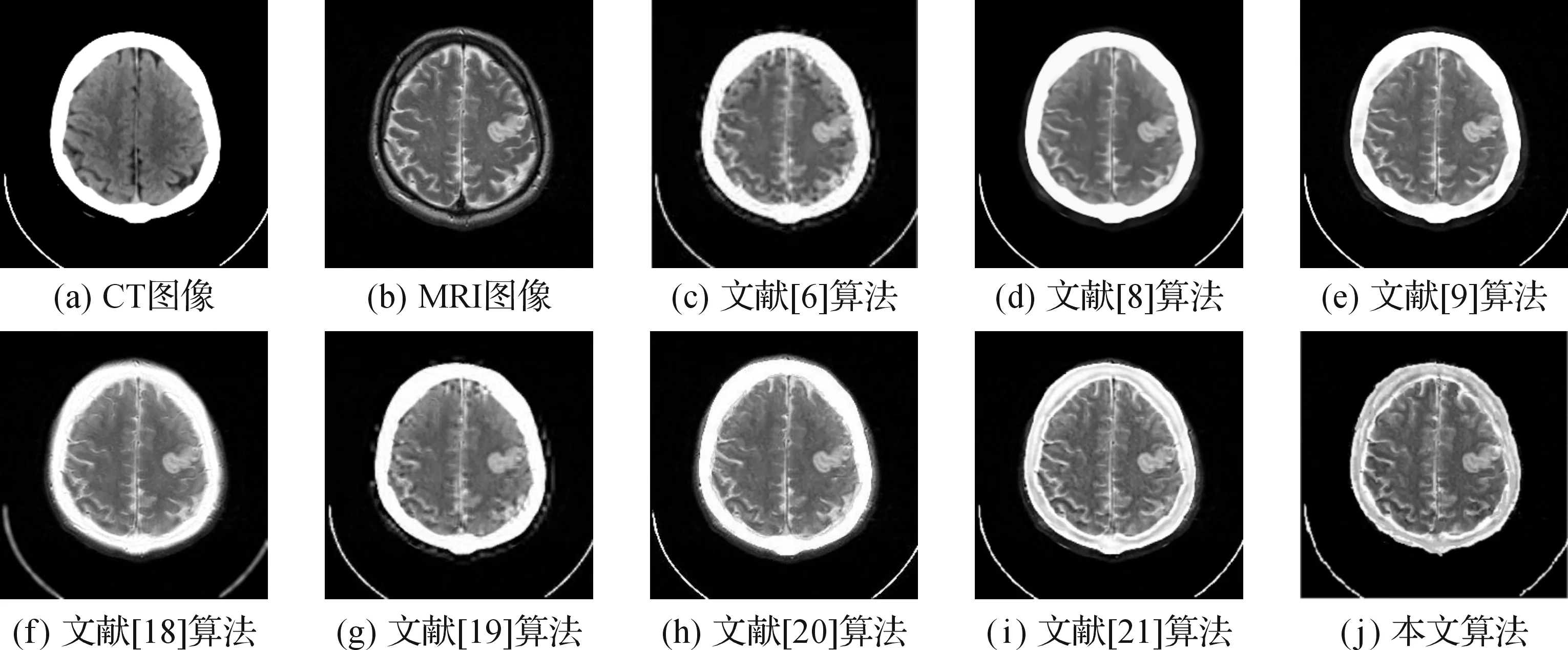
图10 急性脑卒中CT/MRI医学图像融合结果

评价指标文献[6]算法文献[8]算法文献[9]算法文献[18]算法文献[19]算法文献[20]算法文献[21]算法本文算法IE5.86235.86336.06836.09315.82415.72535.93026.0581QABF0.61020.59540.62310.60790.60390.58220.60370.6276SD31.04129.92731.75430.91530.67431.3732.13232.381SF9.36489.48439.21859.52169.07838.86929.37559.4216

表2 不同融合方法处理图9的融合指标

表3 不同融合方法处理图10的融合指标

分析图8-图10不同算法的融合结果图像，可以看出本文算法有着良好的纹理信息，目标边缘更加清晰，不但清晰地保留了源图像的脑部组织信息，而且整体对比度高。分析图9可以看出，图9(c)、图9(e)、图9(f)、图9(h)的图像模糊，对比度低，骨骼和软组织细节信息丢失，无法体现源图像的纹理信息，且出现了频谱混叠现象，源图像信息表现不明显；图9(d)、图9(f)、图9(i)轮廓显示模糊，纹理信息部分丢失；图9(j)不仅保留了空间信息，而且纹理信息和轮廓信息相对丰富。由图10可见，从主观评价分析，对比其他7种融合结果，本文算法对病变部位提取清晰，而且保留了周围组织的丰富信息。因此本文算法的融合结果相比之下伪轮廓最少，且具有相对高的图像对比度和清晰的细节信息。分析表1—表3的图像质量评价指标，可以得出本文算法融合结果的评价指标部分数据最好，综合评价数据良好。表1中QABF与SD表现最好，表2中IE、SD、SF表现最好，表3中IE、QABF、SD表现最好，这表明本文提出的算法包含的信息大，具有更分散的灰度分布，边缘传递好，空间活跃度高。

为了更清晰地分析本文的有效性，图11显示了图8中各文献算法的右下局部放大图。可以看出，图11(a)、图11(e)、图11(f)出现了伪轮廓，且边缘模糊；图11(b)、图11(c)、图11(d)骨骼和软组织重合，无法很好地分辨边界；图11(g)骨骼与软组织明显分离，丢失了细节信息；图11(h)能清晰表现出轮廓及边界，保留了源图像更多的细节信息。

图11 图8中融合图像局部区域放大图

4.2 彩色图像融合

为验证本文算法的实用性，将彩色图像与灰度图像进行融合实验分析。首先通过IHS(Intensity-Hue-Saturation)变换将彩色图像从RGB颜色空间变换到IHS空间，再利用NSCT变换分解I分量图像和灰度图像并用本文算法融合，然后将得到的灰度融合图像替换原来的I分量，最后通过IHS逆变换得到最终RGB彩色图像[22]。融合步骤如图12所示。

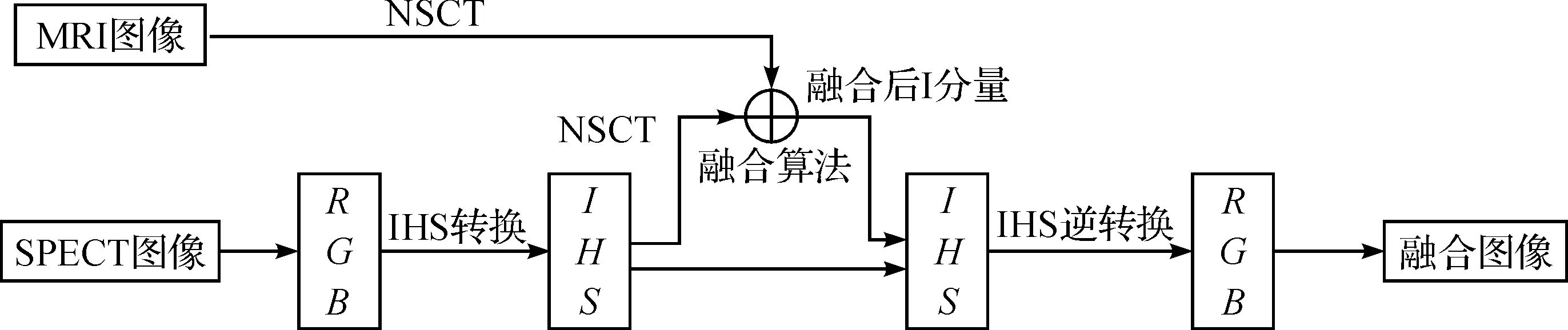
图12 MRI/SPECT图像融合流程图

本次融合图像为24位SPECT彩色图像和8位MRI灰度图像。图13(a)、14(a)为不同组织的SPECT源图像，它能够反映人体组织血流、生理代谢等功能，但分辨率低。图13(b)、14(b)为相对应的MRI源图像，它对血管、软组织成像分辨率高。图13(c)、14(c)为文献[6]提出的融合算法结果图像。图13(d)、14(d)为文献[8]提出的融合规则结果图像。图13(e)、14(e)为文献[9]提出的融合算法结果图像。图13(f)、14(f)为文献[18]提出的融合规则结果图像。图13(g)、14(g) 为文献[19]提出的融合规则结果图像。图13(h)、14(h)为文献[20]提出的融合规则结果图像。图13(i)、14(i)为文献[21]提出的融合规则结果图像。图13(j)、14(j)为本文提出的融合规则结果图像。表4、表5为不同源图像经多种融合算法处理后的图像质量评价结果。

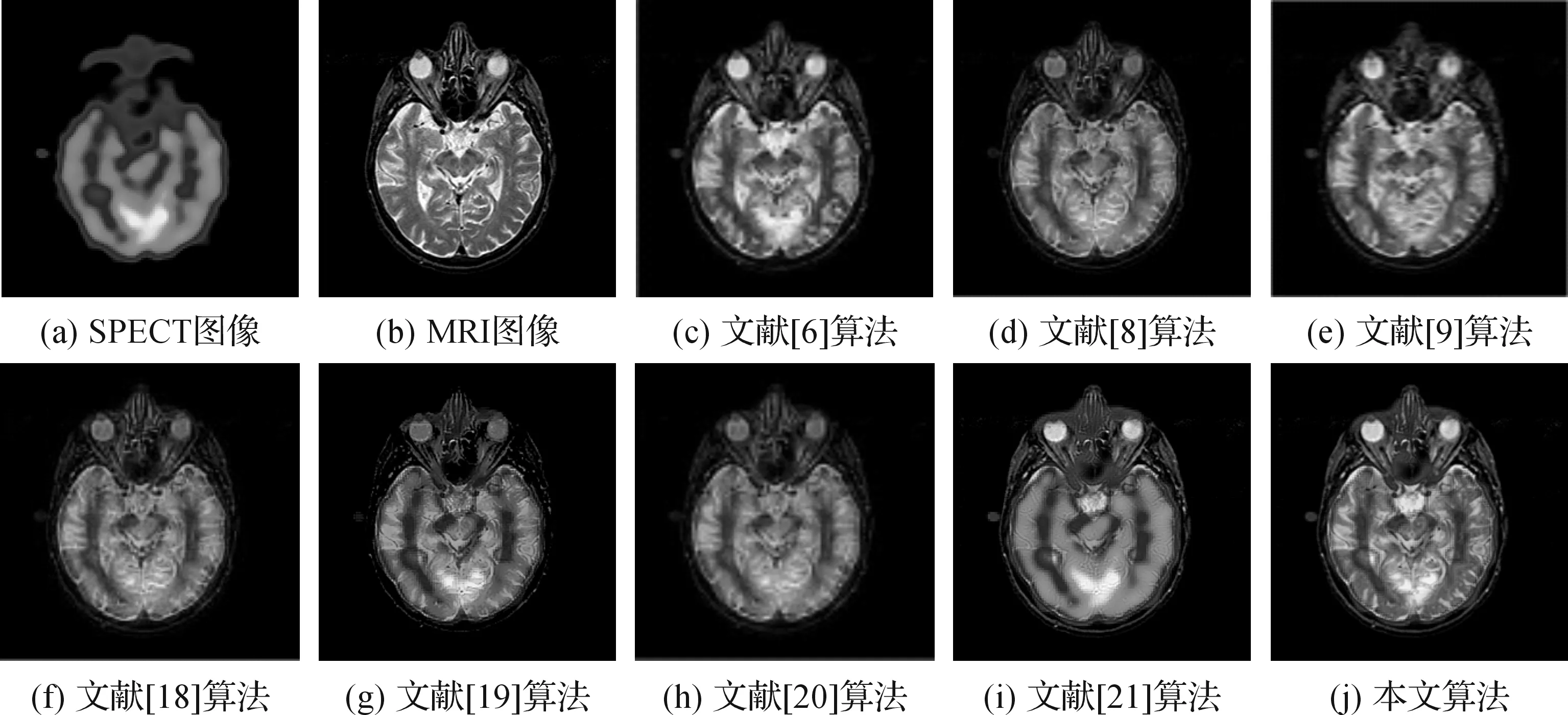
图13 正常脑部SPECT/MRI医学图像融合结果

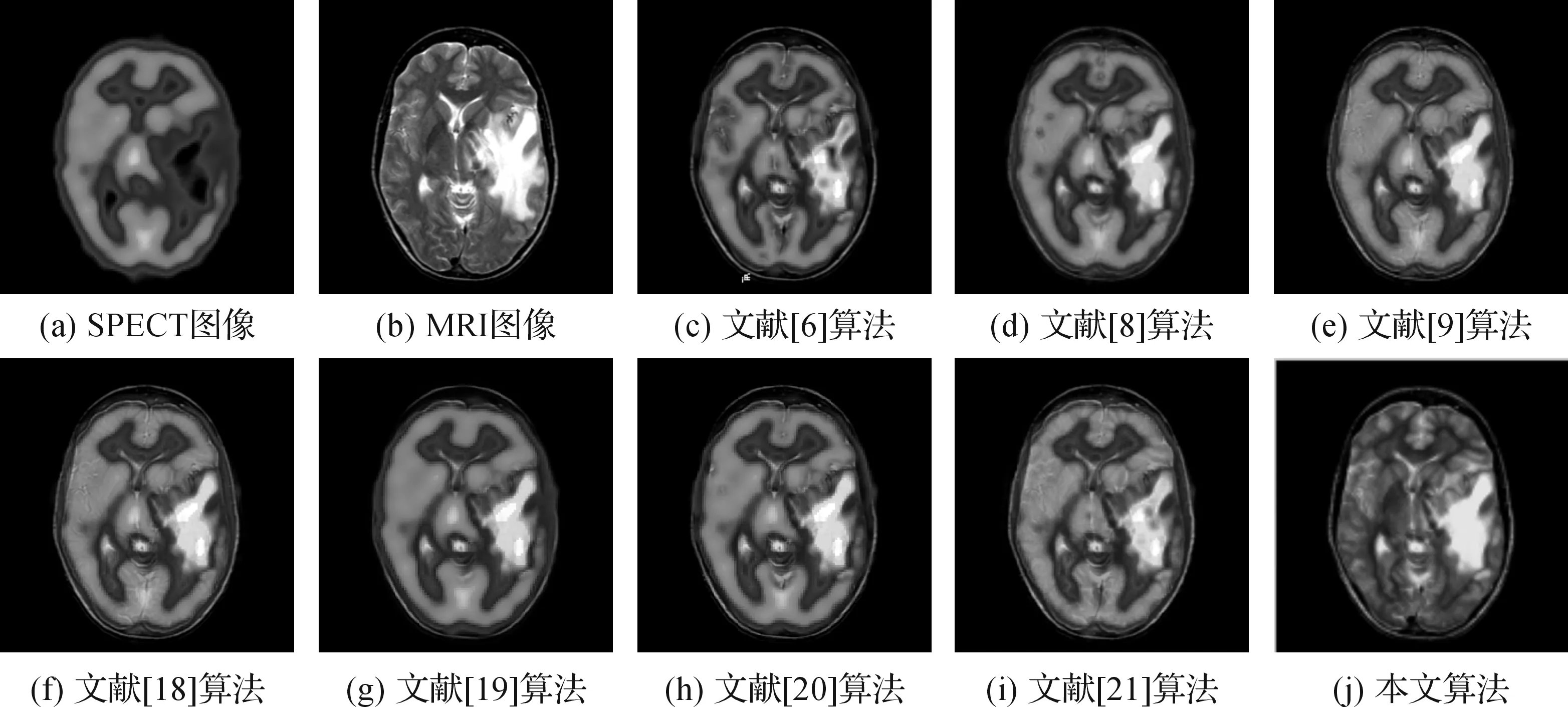
图14 转移性肺癌SPECT/MRI医学图像融合结果

评价指标文献[6]算法文献[8]算法文献[9]算法文献[18]算法文献[19]算法文献[20]算法文献[21]算法本文算法IE4.04264.13784.21504.23873.91284.01274.26714.3264QABF0.60740.57950.67190.66210.64920.63860.58700.6837SD63.85962.14264.32660.37464.74665.01462.71263.469SF17.304617.386416.931217.387516.187315.321616.732417.2320

表5 不同融合方法处理图14的融合指标

分析表4和表5的图像质量评价指标，可以发现本文算法在IE、QABF评价指标数据最好，其他评价数据表现综合良好，说明本文算法保留了源图像更多的信息，并且边缘信息丰富。分析图13、图14不同算法的融合结果图像，可以发现本文算法能很好地保留源图像的纹理边缘信息，比其他算法的融合结果图像更加清晰，解剖结构如血管、软组织等更加明显。分析图14可以看出，本文算法对白色部分病灶提取有效，并且对于病灶周围及边缘信息更加突出。

综上所述，本文算法更具有效性，信息保留更完整，纹理更加清晰，细节信息丰富，能给临床医学对病灶的诊断提供更多的帮助。

5 结 论

本文提出了一种基于纹理特征与广义相关性结构信息的医学图像融合方法，该方法考虑到人眼视觉对纹理特征的敏感性，实验对比结果表明本文的融合新方法保留了更多的轮廓、纹理信息，细节特征更加显著突出，能更好地完整体现病灶部分，视觉效果更佳。

[1] DAS S, KUNDU M K. A neuro-fuzzy approach for medical image fusion[J]. IEEE Transactions on Biomedical Engineering,2013,60(12):3347-3353.

[2] BHATNAGAR G, WU Q M J, LIU Z. Directive contrast based multimodal medical image fusion in NSCT domain[J]. IEEE Transactions on Multimedia,2013,15(5):1014-1024.

[3] WANG L, LI B, TIAN L. Multimodal medical volumetric data fusion using 3-D discrete shearlet transform and global-to-local rule[J]. IEEE Transactions on Biomedical Engineering,2014,61(1):197-206.

[4] DAS S, KUNDU M K. NSCT-based multimodal medical image fusion using pulse-coupled neural network and modified spatial frequency[J]. Medical & Biological Engineering & Computing,2012,50(10):1105-1114.

[5] HEIJMANS H M, GOUTSIAS J. Nonlinear multi-resolution signal decomposition schemes. II. Morphological wavelets [J]. Image Processing, IEEE Transactions on,2000,9(11):1897-1913.

[6]李俊峰,姜晓丽,戴文战.基于提升小波变换的医学图像融合[J].中国图象图形学报,2014,19(11):1639-1648.

[7] YANG Y, QUE Y, HUANG S, et al. Multimodal sensor medical image fusion based on type-2 fuzzy logic in NSCT domain[J]. IEEE Sensors Journal,2016,16(10):3735-3745.

[8] SRIVASTAVA R, PRAKASH O, KHARE A. Local energy-based multimodal medical image fusion in curvelet domain[J]. IET Computer Vision,2016,10(6):513-527.

[9] BHATEJA V, PATEL H, KRISHN A, et al. Multimodal medical image sensor fusion framework using cascade of wavelet and contourlet transform domains[J]. IEEE Sensors Journal,2015,15(12):6783-6790.

[10] CUNHA A L, ZHOU J P, DO M N. The nonsubsampled contourlet transform:theory, design and applications[J]. IEEE Transactions on Image Processing.2006,15(10):3089-3101.

[11] 王相海,倪培根,苏欣,等.非下采样Contourlet HMT模型[J].中国科学:信息科学,2013,43(11):1431-1444.

[12] WANG L, LI B, TIAN L F. A novel multi-modal medical image fusion method based on shift-invariant shearlet transform[J]. The Imaging Science Journal,2013,61(7):529-540.

[13] 李俊峰,张飞燕,戴文战,等.基于图像相关性和结构信息的无参考图像质量评价[J].光电子(激光),2014,25(12):2407-2416.

[14] 杨赛,赵春霞,徐威.一种基于词袋模型的新的显著性目标检测方法[J].自动化学报,2016,42(8):1259-1273.

[15] 朱烨,李晓斌.改进差分盒维数阈值的自然图像分割方法[J].计算机仿真,2015,32(4):197-201.

[16] TZENG Y C, FAN K T, CHEN K S. A parallel differential box-counting algorithm applied to hyperspectral image classification[J]. IEEE Geoscience and Remote Sensing Letters,2012,9(2):272-276.

[17] 何龙兵,那彦.多光谱可见光图像与高分辨率图像的分维融合[J].电子科技,2011,24(1):4-8.

[18] 陈震,杨小平,张聪炫,等.基于补偿机制的NSCT域红外与可见光图像融合[J].仪器仪表学报,2016,37(4):860-870.

[19] 李加恒,戴文战,李俊峰.基于互信息的多模态医学图像融合[J].浙江理工大学学报,2016,35(4):607-614.

[20] 徐卫良,戴文战,李俊峰.基于提升小波变换和PCNN的医学图像融合算法[J].浙江理工大学学报,2016,35(6):891-898.

[21] 殷鑫华,戴文战,李俊峰.基于在线字典学习的自适应医学图像融合算法[J].浙江理工大学学报,2016,37(3).

[22]李光鑫,王珂.基于Contourlet变换的彩色图像融合算法[J].电子学报,2007,35(1):112-117.

(责任编辑： 康 锋)

Medical Image Fusion Algorithm Based on Textural Features and Generalized Correlation Structure Information

PANShuwei1,DAIWenzhan2,LIJunfeng1

(1. Institute of Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China; 2. School of Information and Electronic Engineering, Zhejiang Gongshang University, Hangzhou 310018, China)

According to the characteristics of multi-scale transform, a medical image fusion algorithm based on textural features and generalized correlation structure information is proposed. Firstly, nonsubsampled contourlet transform is conducted for registered source images to get low-frequency and high-frequency sub-band coefficients. Secondly, considering the sensitivity of human eye vision to the textural feature, local differential box counting dimension is used to collect textural information of images, We analyze the strong correlation between brother coefficients and father-son coefficients respectively in high frequency sub-bands of NSCT. Moreover, structure similarity in those coefficients and the sum of Laplace energy between of neighborhoods are calculated as generalized correlation structure information of high frequency sub-band coefficients. Thirdly, Sigmoid function self-adaption fusion is proposed on low frequency sub-bands, and absolute value rule of generalized correlation structure information is presented on high frequency coefficients. Finally, the fused image is obtained by performing the inverse NSCT. It is found through gray level and color image fusion experiment that, the proposed approach can preserve marginal information of source images effectively and improve the objective evaluation index and visual quality.

medical image fusion; nonsubsampled contourlet transform; local differential box counting dimension; generalized correlation structure information

10.3969/j.issn.1673-3851.2017.05.019

2016-10-16 网络出版日期：2017-01-03

国家自然科学基金项目(61374022)

潘树伟(1990-)，男，浙江湖州人，硕士研究生，主要从事模式识别与图像处理方面的研究。

戴文战，E-mail: dwz@zisu.edu.cn

TP391.4

A

1673- 3851 (2017) 03- 0423- 09