基于能量梯度理论的回流器入口安装角对离心压缩机性能影响研究

陈 兴，窦华书，陈小平，魏义坤，梁迦贺，孙玉莹，卢傅安，刁 全

(1.浙江理工大学机械与自动控制学院，杭州 310018；2.沈阳鼓风机集团股份有限公司，沈阳 110000)



基于能量梯度理论的回流器入口安装角对离心压缩机性能影响研究

陈 兴1，窦华书1，陈小平1，魏义坤1，梁迦贺1，孙玉莹2，卢傅安2，刁 全2

(1.浙江理工大学机械与自动控制学院，杭州 310018；2.沈阳鼓风机集团股份有限公司，沈阳 110000)

利用定常的三维Navier-Stokes方程和Spalart-Allmaras (S-A)湍流模型，对不同回流器入口安装角的离心压缩机级性能进行了数值模拟；并利用能量梯度理论对不同入口安装角下的回流器内部的流动状况进行分析，得到每一种模型的能量梯度函数K的分布。结果表明：在设计工况下，回流器入口安装角在37°附近时多变效率和压比最高；通过对不同工况下的回流器进行能量梯度函数K值分析，发现回流器内流动最容易失稳的地方主要处于回流器叶片的尾部及出口位置，且相对其他流量工况，设计工况下回流器内的流动最稳定；分析不同入口安装角回流器沿轴向不同截面的K值分布，发现在37°～46°范围内的K值最小，回流器内的流动较为稳定；同一回流器中，越靠近轮盖位置，流动越容易出现不稳定。

离心压缩机；回流器；入口安装角；能量梯度

0 引 言

在机械工程领域，涡轮机械是一种可以将能量在流体介质和转子部件之间进行转换和传递的机械装置。压缩机和涡轮机是比较常见的涡轮机械。其中离心压缩机具有结构紧凑，工作可靠高效和经久耐用等特点，在整个工业领域有着广泛的应用[1]。

在多级离心压缩机中，回流器作为两级离心压缩机之间的固定元件，主要起到将上一级扩压器出口的旋转气流按所需的方向引入下一级叶轮的作用。但是，在回流器中气流的摩擦损失较大，回流器的出口气流影响了下一级叶轮的进口气流条件，从而影响离心压缩机级性能，因此改善回流器中的流动十分重要。

二十世纪九十年代以来，许多国内外学者对离心压缩机的回流器做了试验和数值模拟，取得了一系列成果。郭建平等[3]通过回流器内部的理论分析和不同形式回流器的实验测试，着重研究了回流器内部的流动特征以及回流器叶片型式对回流器性能及压缩机级特性的影响规律。姚承范等[4]研究表明，回流器叶片型式对离心压缩机级的喘振极限和级效率都有一定的影响，采用最小扩压度回流器能有效地降低喘振极限而保持较高的效率。高星等[5]对比分析了进口流场、叶片数、负荷分布形式对回流器内部流动结构和性能的影响，发现改善进口流场和增加叶片数能够抑制回流器内的二次流，并增加回流器出口流场均匀性。Lenke等[6]采用低雷诺数k-ε模型和显式代数应力模型，分别对多级离心压缩机的内部流动进行了数值模拟，发现在设计工况下两个模型对分离损失、气流角的预测差别较小。Veress等[7]提出了一种离心压缩机回流器反设计与优化的方法。Nishida[8]采用遗传算法对离心压缩机回流器进行了多目标优化，使效率和压力系数分别提升了1.0%和3.2%。尽管前人已经对回流器内的流动状况及回流器的设计方法进行了大量研究，但是关于回流器内流动稳定性的探讨尚未深入，对如何减小回流器内的流动损失的研究较少。本文使用CFD方法计算分析了回流器入口安装角对离心压缩机级性能影响，确定了最佳入口安装角的范围，并应用能量梯度理论对回流器内部流场进行处理，获得了不同工况下的能量梯度函数K值的分布，确定回流器内部流动流动失稳的部位以及沿轴向方向不同位置的流动稳定性，这对回流器的设计及改善回流器内的流动状况具有很大的意义。

1 控制方程与计算方法

1.1 数值模型

本文采用Numeca软件对离心压缩机进行数值模拟，求解的控制方程为三维雷诺平均N-S方程，采用的湍流模型为叶轮机械模拟适应性较好的Spalart-Allmaras (S-A)湍流模型[9]。设置的边界条件是总温总压入口、质量流量出口，叶片的表面与内外壁均采用无滑移边界条件，在动静结合面上采用周向守恒型连接面的连接形式。

采用的模型对象是沈阳鼓风机集团股份有限公司所用LB56150 KY108离心压缩机模型级，主要研究其回流器内部的流体的流动特性。该离心压缩机由闭式叶轮、叶片扩压器、回流器组成，原离心压缩机模型的主要参数如表1所示。

表1 原离心压缩机主要参数

图1为压缩机三维模型及单流道网格示意图。本文研究的原模型的回流器入口安装角为46°。所改变的不同入口安装角分别为25° 、30° 、37° 、46° 、50° 、55° 、65°。对离心压缩机整级单流道进行结构网格划分，总网格数为236万，其中叶轮网格数94万，扩压器网格数60万，回流器网格数约82万，网格在叶片周围边界层以及叶轮叶片出口处都进行了加密。第一层的网格厚度0.01 mm，满足湍流模型的计算要求。

图1 离心压缩机三维模型及网格示意图

1.2 能量梯度理论

能量梯度理论[10-13]是基于牛顿力学与Navier-Stokes方程提出的一种用于分析流动稳定性和湍流转捩问题的新理论，运用该理论分析Taylor-Couette流动、plan-Couette流动、plan-Poiseuille和pipe-Poiseuille等流动得到的结果，均与实验数据吻合较好。此外，贲安庆等[14]运用能量梯度理论分析了机翼绕流的流动稳定性并发现了最易产生失稳的位置。张斌炜等[15]运用能量梯度理论对双吸离心通风机的内部流动稳定性进行分析，发现在叶道子午面上越接近轮盖处的位置流动越容易出现不稳定。郑路路等[16]运用能量梯度理论分析了叶片数对离心泵内部流动稳定性的影响，找到了使细离心泵效率最佳稳定工作区域最大的叶片数。

(1)

(2)

其中：E为流体总压；P为静压；U为流体总速度；H为流体流线方向上的能量损失；n为流体流动的法线方向；s为流体流动的流线方向；ρ为流体的密度；μ为流体的粘度。

式(1)表示的是可压缩剪切驱动流动公式，式(2)表示的是可压缩压力驱动流动公式。K值为无量纲流场函数，等于法向能量梯度与流向能量损失的比值。当流场中的扰动变化不大时，在层流状态下，K值越大的位置，流动越容易发生失稳，越容易向湍流转捩；在湍流状态下，K值越大的位置，湍流强度越高。因此，K值能够准确预测出流动产生失稳的位置，便于控制流体流动[18]。

2 计算方法与网格无关性验证

2.1 网格无关性验证

本文采用网格数分别为205万、239万和272万三套网格，在最大流量工况分别进行计算，选取最大流量工况下多变效率作为参考值，具体计算结果如图2所示。

不同网格工况下算得的多变效率值如图3所示，随着网格数量的增大计算多变效率趋于稳定，当采用205万的计算网格时，计算结果与实验值的误差相对较大，而采用239万网格和272万网格的计算结果接近，说明此时网格的密度对计算结果的精度影响不大。本文选取的计算网格数为239万。

图2 网格无关性

2.2 计算结果验证

图3为多变效率和压比的实验值与数值模拟值对比图。在小流量工况下，无论是效率还是压比，实验值略大于计算值，而且随着流量的增大，两者差距逐渐变小，总体呈吻合趋势；在大流量工况时，计算值比实验值略大，但是在数值上偏差较小。造成误差的因素主要是数值计算本身受湍流模型、网格质量以及几何模型型线简化的影响，还有实验本身的测量手段和数据处理也会存在一定的误差。

图3 原模型实验值与数值模拟值对比

3 计算结果与讨论

3.1 回流器入口安装角对级性能的影响

图4为回流器入口安装角α5A分别为25° 、30° 、37° 、46° 、55° 、65°(其中46°为离心压缩机原模型的回流器的入口安装角)的离心压缩机多变效率-流量曲线以及压比-流量曲线。从图4(a)中发现，在小流量工况下，α5A对压缩机的性能的影响不是很大，随着α5A发生变化，几个模型的多变效率变化较小。同样地如图4(b)所示，在小流量下压比的变化也很小。而随着工况流量的逐渐增大，α5A变化对多变效率和压比带来的影响逐渐变大。特别是在大流量工况下，α5A在46°～65°的范围内，随着α5A的增大，压缩机级多变效率和压比逐渐下降。在α5A=25°～46°范围内，压缩机的级效率和压比较高，且α5A的变化对多变效率和压比的影响不太大，并在α5A=37°时，压缩机的级多变效率和级压比最高。

3.2 不同流量下回流器内部稳定性分析

图5为小流量(Qm=6.01 kg/s)、设计工况流量(Qm=6.61 kg/s)以及大流量(Qm=7.65 kg/s)三个工况下回流器内的K值分布，其中白灰色为K值较大区域，K值越大，表明湍流强度越大，越不稳定。从图6中可以看出，在回流器叶片尾部以及出口部分，K值的大小基本都在500以上，说明在这些位置流动容易发生失稳。这是因为回流器的出口位置紧接着将气流引入下一级的180°弯道，当气流达到弯道外侧时，受较大离心力的影响，能量梯度变化较大，所以造成气流在此处的稳定性较差。对比图5(a)-(c)三种不同流量工况，回流器中的K值分布比较类似。其中在大流量下，与小流量和设计流量下相比，可能由于回流器入口的气流负冲角较大，回流器尾部的K值明显增大，说明在大流量下回流器内的流动更加不稳定。

图5 不同流量下原模型回流器内K值分析

3.3 不同入口安装角回流器内部稳定性分析

由前面的不同工况下回流器内的K值分析可知，不同工况对回流器内的稳定性影响不大，在设计工况下的回流器内部流动比其他流量下更加稳定，因此，选择在设计工况下分别对入口安装角α5A等于25° 、30° 、37° 、46° 、55° 、65°的回流器进行K值分析。根据能量梯度理论，K值越大的地方，流动越不稳定，越容易发生失稳。从图6(a)中，即α5A=25°时，在回流器吸力面及尾部部分的K值分布较大，说明在此角度下回流器内部的流动不是很稳定。随着角度的增大，对比α5A=30°与α5A=37°可以发现，其回流器内部的K值分布逐渐减小，说明回流器内的流动状况逐渐改善。再对比图6(d)—(f)可以发现随着角度增大，在回流器叶片尾部大K值的区域逐渐增加，并且越靠近叶片表面的地方K值越大，说明在回流器尾部流动极易发生失稳。这是因为随着的逐渐增大，气流入口冲角(i=α5A-α5)逐渐增大，当冲角大到一定程度，就容易在叶片表面形成边界层分离，产生漩涡，流动也就容易发生失稳。

图6 不同入口安装角回流器内部K值分析(Qm=6.61 kg/s)

图7对比了设计工况下不同入口安装角的回流器内中截面上的压力分布。当入口安装角α5A=25°时，回流器表面压力变化的梯度从入口处延伸到出口处，但是变化梯度较小。当α5A逐渐增大时，总压开始减小的位置逐渐向叶片的尾部转移，说明总压的损失情况在逐渐减小。但是当α5A开始大于46°时，在回流器尾部的压力梯度明显开始增大，压力损失十分严重，在回流器出口位置总压分布也十分紊乱，这与前面K值分析的结果是一致的，说明该位置的流动易发生失稳，且角度很大时失稳情况更加严重。

图7 不同入口安装角回流器内压力分布云图(Qm=6.61 kg/s)

从图7中看出，回流器吸力面总压变化的程度比较明显，因此选取各个回流器叶片吸力面上的总压分布进行统计，结果如图8所示。从图中可以看出，当α5A=25°～37°时，从回流器入口到出口总压分布均匀，压力减小的趋势较小。而角度进一步扩大时，总压沿着叶片表面的波动程度增大，如α5A=65°时，总压在入口先是急剧增大，然后快速回落，衰减程度十分明显，能量损失较大。

图8 不同入口安装角回流器叶片吸力面压力分布(Qm=6.61 kg/s)

3.4 不同回流器截面上的平均K值比较

为了进一步更加精确地说明不同的入口安装角对于回流器内部稳定性的影响，取各模型的设计工况(Qm=6.61 kg/s)与大流量工况(Qm=7.65 kg/s)作为计算工况，分别截取回流器内部不同叶高截面位置进行K值分析。回流器内所取的截面示意图如图9所示。其中截面1位置靠近回流器轮盘，2截面位于回流器叶高中间位置，截面3的位置靠近回流器轮盖。3个截面上不同入口安装角的回流器内部的K值比较结果见图11，对比图10(a)与(b)中的三条曲线可以发现，回流器沿轴向上的内部不

同位置气体流动的稳定性也有很大的差异。靠近轮盖部分的截面平均K值最大，靠近轮盘部分的截面平均K值最小，在中间截面上平均K值居中，说明回流器内部不同的区域，流动稳定性情况也不相同，沿轴向越接近回流器轮盖位置，其内部能量梯度分布大，气体流动越容易出现不稳定。图11显示了α5A=37°的回流器的三个截面的K值云图，对比图11(a)-(c)可以发现，截面1的大K值区域最小，而沿着轴向到了截面2位置，叶片尾部及出口位置K值有所增加，说明能量梯度逐渐增大，而到了截面3位置，白色区域几乎布满整个流道，说明此截面的K值最大，此位置的流动最为不稳定。

图9 流场截面位置示意图

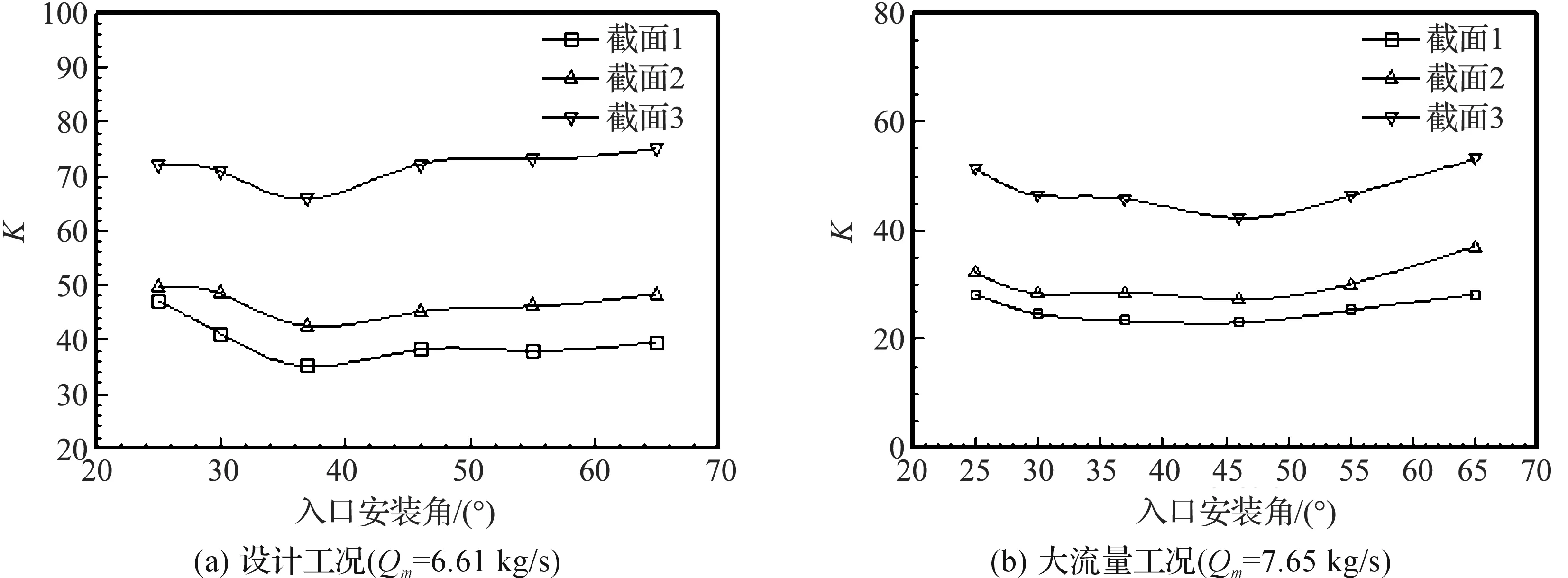
图10 回流器不同叶高截面平均K值大小

图11 设计工况下α5A=37°回流器内部截面的K值分布

无论在设计工况(Qm=6.61 kg/s)还是在大流量工况(Qm=7.65 kg/s)下，截面平均K值先随着α5A的增大先减小后增大，K值最小的位置出现在37°～46°附近，说明在此角度下的回流器内的流动稳定性最好，而在此范围外减小或者增大α5A，K值都会增加，都会引起回流器内流动的失稳，这与前面的性能曲线的分析一致。对比三个截面K值随α5A变化的幅度，由于截面1靠近轮盘的位置，此处流速最小，流动最为稳定，因此α5A的变化对此位置的流动稳定性影响不大，截面1的K值变化幅度最小。截面3靠近轮盖位置，此处的流动最为复杂，所以改变对回流器内的整体流动影响较大，K值变化的幅度也较大。

综上所述，从回流器轮盖到轮盘的位置，K值分布大幅提高，表明回流器内越靠近轮盖的位置流动越不稳定。设计回流器时应该把回流器入口安装角控制在37°～46°范围内，此范围内回流器中的流动稳定性最好。

4 结 论

本文利用定常的三维Navier-Stokes方程和Spalart-Allmaras (S-A)湍流模型，对不同回流器入口安装角(25°、30°、37°、46°、55°、65°)的离心压缩机性能进行数值模拟，与原始模型进行了对比，数值模拟结果与实验结果一致性较好。主要结论如下：

a) 改变回流器入口安装角对离心压缩机级多变效率产生一定影响。在小流量工况下，改变回流器入口安装角，级多变效率改变不大。在大流量工况下，随着回流器入口安装角的增大，级多变效率逐渐下降。在设计工况下，37°入口安装角压缩机级多变效率最高。

b) 不同流量工况对回流器内的K值产生影响。随着流量的增大，K值增大。在径向方向上，回流器叶片尾部及出口位置K值较大，容易发生流动失稳。

c) 入口安装角的改变会影响回流器内部的流动状况。入口安装角α5A为37°～46°的回流器内部流动比较稳定。而入口安装角α5A大于46°的回流器内部流动容易发生失稳。

d) 通过能量梯度理论分析发现，回流器沿轴向方向的不同位置流动稳定性不相同，沿轴向越接近轮盖处，流动越不稳定。

[1] 刘洋.回流器入口冲角对压缩机性能影响的研究[D].辽宁:大连理工大学,2013:1-2.

[2] 徐忠.离心式压缩机原理[M].北京：机械工业出版社,2004:2-3.

[3] 郭建平,姚承范,朱营康.离心压缩机回流器内部流动分析[J].流体工程,1992,20(3):16-21.

[4] 姚承范,朱营康,马林,等.回流器对离心压缩机级特性影响的试验研究[J].工程热物理学报,1991,15(1):46-49.

[5] 高星,刘宝杰.双级离心压缩机回流器流动特点分析[J].航空动力学报,2009,24(2):432-438.

[6] LENKE L J, SIMON H. Numerical simulation of the flow through the return channel of multi-stage centrifugal compressors[C]// Proceedings of ASME Turbo Expo 1998. New York,1998:696-702.

[8] NISHIDA Y. Performance improvement of a return channel in a multistage centrifugal compressor using multiobjective optimization[J]. Journal of Turbomachinery,2013,135(3):420-431.

[9] WILCOX D. Turbulence modeling: An overview[C]// 39th Aerospace Sciences Meeting and Exhibit. Washington, D.C., 2001: 2001-0724.

[10] DOU H S. Physics of flow instability and turbulent transition in shear flows [J]. International Journal of Physical Science,2006(6):1411-1425.

[11] DOU H S, KHOO B C, YEO K S. Instability of Taylor-Couette flow between concentric rotating cylinders[J]. International Journal of Thermal Sciences,2008,47(11):1422-1435.

[12] DOU H S, KHOO B C. Criteria of turbulent transition in parallel flows [J]. Modern Physics Letters B, 2010, 24 (13):1437-1440.

[13] DOU H S, KHOO B C, et al. Investigation of turbulent transition in plane couette flows using energy gradient method[J]. Advances in Applied Mathematics & Mechanics,2005,3(2):141-147.

[14] 贲安庆,窦华书.可压缩机翼绕流的数值模拟及其稳定性分析[J].浙江理工大学学报,2015,33(9):675-681.

[15] 张滨炜,窦华书,魏义坤,等.基于能量梯度理论双吸式离心通风机失稳研究[J].工程热物理学报,2015(9):1917-1921.

[16] 郑路路,窦华书,蒋威,等.基于能量梯度方法的叶片数对离心泵稳定性影响研究[J].浙江理工大学学报,2016,35(1):71-77.

[17] BEN A Q, DOU H S. Simulation and stability study of the flow around a cylinder in infinite domain[J]. Procedia Engineering,2015,126(2):68-72.

[18] 窦华书,肖美娜.用能量梯度理论研究180度弯管内流动失稳[J].工程热物理学报,2013,34(4):658-661.

(责任编辑： 康 锋)

Effect of Return Channel Stagger Angle on Performance of Centrifugal Compressor Based on Energy Gradient Theory

CHENXing1，DOUHuaShu1，CHENXiaoping1，WEIYikun1，LIANGJiahe1，SUNYuying2，LUFuan2，DIAOQuan2

(1. Faculty of Mechanical Engineering and Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China；2. Shenyang Blower Works Group Corporation, Shenyang 110000, China)

Steady three-dimensional Navier-Stokes equations and the Spalart-Allmaras turbulent model are used for numerical simulation of centrifugal compressor performance with different return channel stagger angle. The energy gradient theory is applied to analyze the flow field in return channels. The distribution of the energy gradient functionKis obtained for each model. The results show that under the design conditions, the stage performance comes to the best when return channel stagger angle equals to 37°. According to the analysis of energy gradient functionKin different conditions, it is found that the instability easily happens in the tail and exit position of the return channel blade and the flow field is more stable under the design conditions. Distribution ofKvalues along the axial direction of different models are analyzed and found thatKvalue is the smallest within 37°～46°, and the flow in the return channel is stable. In the same return channel, the flow return channel may easily happen near the hub.

centrifugal compressor; return channel; stagger angle; energy gradient theory

10.3969/j.issn.1673-3851.2017.05.015

2016-10-18 网络出版日期：2017-01-03

国家自然科学基金项目(51579224)

陈 兴(1992-)，男，浙江温州人，硕士研究生，主要从事离心压缩机方面的研究。

窦华书，E-mail: huashudou@yahoo.com

TH452

A

1673- 3851 (2017) 03- 0394- 08