客车盘式制动器温度场仿真分析

刘 艳，陈燕峰，吴跃成，胡旭晓

(浙江理工大学机械与自动控制学院，杭州 310018)



客车盘式制动器温度场仿真分析

刘 艳，陈燕峰，吴跃成，胡旭晓

(浙江理工大学机械与自动控制学院，杭州 310018)

以某客车配套制动器为研究对象，首先应用Catia软件建立相应的制动盘三维模型，然后用HyperMesh软件对制动盘进行网格划分，最后用Abaqus软件对其进行热结构直接耦合分析。讨论了热流密度和对流散热系数的计算方法，比较了单次和多次连续制动的温度场云图，分析了不同工况下制动盘摩擦表面最高温度的变化规律。结果表明：单次制动时，制动盘的温度在轴向有一个较大的梯度变化，周向上分布均匀，最高温度达258.6 ℃；多次连续制动后，摩擦表面温度场周向差异逐渐减小，制动盘温度场的分布逐渐趋于轴对称分布；制动过程中，制动盘的最高温度随客车载重和初速度的增加而增加。研究结果可为制动盘的工况选择、制动盘破坏预防等提供参考。

客车；盘式制动器；温度场；有限元法

0 引 言

制动器是车辆制动系统中用以产生阻碍车辆运动或相对运动趋势的力的部件，其性能的稳定性直接影响车辆的安全[1]。由于盘式制动器的制动效能更加稳定，因此，目前货车和客车都在推广使用盘式制动器。但由于盘式制动器制动压力大，制动产生的摩擦热会导致摩擦副热变形，影响接触应力，导致制动盘出现热裂纹，使其使用寿命减少。国内外学者进行了大量研究。Adamowicz等[2]建立了简化的有限元模型，计算出实心盘的温度分布情况，得出了紧急制动时二维和三维实心盘式制动器的温度场分布特点，但建立的是相对理想化的轴对称模型；Duzgun[3]探讨了不同结构的制动盘对摩擦副温度场影响，发现通风盘式制动器的最高温度远比实心盘的温度低，但并未分析制动工况对温度场的影响；Belhocine等[4]建立了三维盘式制动器热结构耦合模型，但研究对象是制动压力相对较小的汽车；朱咏梅等[5]和尹安东等[6]则是采用Abaqus软件建立了三维有限元模型，分析了摩擦系数和比热对温度场的影响，得出最佳制动盘的物理参数。

本文针对某客车的盘式制动器，建立了三维有限元模型，分析了在较高制动压力情况下制动盘的温度场分布规律，比较了多次连续制动的情况下制动盘温度场变化情况，以及制动盘的工况对温度场的影响，为制动盘的结构优化提供参考数据。

1 制动盘热分析及相关计算

1.1 制动盘产热原理分析

在制动过程中，制动盘与摩擦片的接触运动是一个将动能转化为摩擦生热的能量转化过程。摩擦副的接触面产生大量热，会导致制动副的温度场发生较大变化，从而影响摩擦面的热流输入变化，进而对制动摩擦副温度场的分布规律产生影响[7]。

用Abaqus软件对客车前盘制动器进行有限元分析时，制动盘运行的速度、工况参数以及热分析必须设定三类条件[8]。第一类边界条件规定模型初始边界温度，本文设置为20 ℃。第二类边界条件选定制动盘周围气流的温度以及周围气流的对流换热系数。第三类边界条件本文只考虑热传导和热对流对摩擦副温度场的影响，由于制动时间短且温升不是太高，因而不考虑热辐射对摩擦副温度场的影响。

1.2 热流密度计算

制动过程中的热应力变化过程，是车辆动能转化为摩擦生热和克服阻力做功的过程[9]。在该过程中，摩擦生热的能量一部分被地面消耗，大部分被制动盘和摩擦片吸收。分析过程中，直接将摩擦副吸收的能量转化成热流密度施加在制动盘摩擦表面。

制动时客车质心前移，前、后轴的质量GF、GR可由式(1)计算：

(1)

其中：G为客车满载时的质量；L为客车的轴距；Hg为质心高度；R为车轮的滚动半径；GF为前轴质量；GR为后轴质量；a为质心到前轴的距离；b为质心到后轴的距离。

前后轴制动力分配系数为：

(2)

前轴一侧车轮的制动功率P可由式(3)计算：

(3)

热流密度Sh可由式(4)计算：

(4)

其中：V0为制动初速度，取值为70 km/h；a0为客车制动减速度，取值为6 m/s2，S为摩擦面积，取值为0.298 m2；η为能量传递到制动盘的比例，取值为0.9。

2 制动盘有限元模型的建立

2.1 制动盘三维模型简化及网格划分

以某国产客车的前盘通风制动器为研究对象，先在Catia中建立简化的三维模型，如图1所示，然后导入Abaqus中建立有限元模型，分析制动盘的温度场分布规律。制动盘的网格划分模型如图2所示。网格单元采用C3D4T热结构耦合的专用单元，在保证计算精度的前提下，能对制动盘进行合理的单元尺寸划分。制动盘的材料为HT250，计算分析所需的尺寸和材料参数见表1—表4。

图1 制动盘和摩擦片的三维模型

图2 摩擦盘的网格划分

前桥轴荷/kg5500后桥轴荷/kg11000轴距/mm5550质心高度/mm700质心到前轴距离L1/mm3700质心到后轴距离L2/mm1850前轮等效转动惯量/(kg·m2)879制动盘与摩擦片的名义接触面积/cm2920.81

表2 制动器的结构参数

表3 制动盘的物理参数

表4 热传导系数

2.2 模型传热参数的确定

对流散热是指流体流经固体表面时，与固体表面发生的热量传递现象[10]。在制动过程分析中，对流换热系数hc是随着制动盘的转速不断变化的。对于通风的盘式制动器需要考虑两种不同的散热方式，分别是摩擦盘表面与空气的散热和通风孔与空气的对流散热作用。

对于实心盘式制动器，由文献[11]盘式制动器制动的经验公式，得：

(5)

其中:ka为空气的热传导系数；D为制动盘的外径；Re为雷诺数，其中Re=ωRρaCa/μa，ω为制动盘的角速度，ρa为空气密度，μa为空气粘度。

根据文献[12]，热传导系数ka=0.0276 W/(m·K)，密度ρa=1.13 kg/m3，运动粘度μa=1.91×10-5kg/ms，比热Ca=1.005 kJ/(kg·K),以上数据代入式(5)可得，制动盘的对流系数与其转速的表达关系式：

(6)

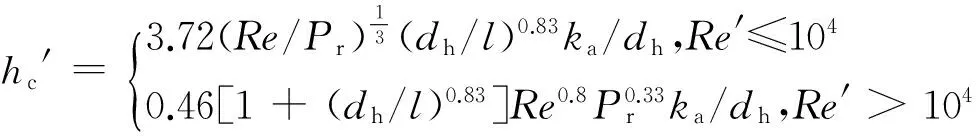
(7)

Re′=Vqρadh/μa

(8)

(9)

(10)

L=(D0-Di)/2

(11)

(12)

(13)

3 仿真分析结果

3.1 单次制动温度场分析

在单次制动时，制动盘有一个快速升温的过程，然后温度升高相对缓和，最后会有所下降，如图3—图4所示。这是因为摩擦副开始接触时，对流散热和热传导的作用远小于摩擦生热产生的热量；制动进行一段时间后，由于对流散热的作用，使热量与空气有个热交换，传递了一部分热量，同时，由于热传导使制动盘摩擦表面的热传递到制动盘内部，导致升温相对缓和；后期，制动盘的转速明显减缓，由于对外散热和热传递的作用大于摩擦生热，温度出现一个下降的过程。

图3 第一次制动制动盘的最高温度变化

图4 连续10次制动制动盘的最高温度变化

3.2 连续制动温度场变化

在实际制动过程中，制动盘的失效情况一般都是长时间连续制动导致的。本文分析了连续十次制动，每次制动时间间隔30s的过程。由结果分析得，第一次制动后制动盘的最高温度为258.6 ℃，连续十次制动后最高温度为637.5 ℃，冷却30s之后，最高温度迅速降为398.9 ℃。图5—图8给出单次制动和连续十次制动后情况，从图中可以看出，一次制动后主要是两侧的摩擦表面快速升温，摩擦盘中部升温缓慢，但多次连续制动后，在对流散热和热传导的综合作用下，制动盘的温度由内到外都显著的升高。由图3—图4给出的制动过程中温度变化曲线可知，随着制动次数的增加，制动盘的最高温度也在显著增加；30s的冷却时间使制动盘的温度快速降低。

图5 第1次制动后制动盘的温度场

图6 第1次制动冷却后制动盘的温度场

图7 第10次制动后制动盘的温度场

图8 第10次制动冷却后制动盘的温度场

3.3 最高温度的影响因素

在实际制动过程中，每次制动的工况和客车本身的参数都是变化的。为了更加准确了解制动盘的温度场变化规律，本文主要从改变制动初速度和客车总质量这两个方面来分析。用Abaqus软件计算了几种不同数据下制动盘的最高温度的变化，其结果如图9—图10所示。随着制动初速度的增加，制动盘表面的最高温度在增加；客车载重增加，制动盘表面的最高温度也会有个显著提升，其中初速度对最高温度的影响较大,且客车初速度、客车载重与制动盘表面的最高温度存在近似线性关系。

图9 不同初速度制动盘的最高温度

图10 不同载荷下制动盘的最高温度

4 结 论

a) 客车盘式制动器单次制动后，制动盘的温度在轴向上有较大的梯度变化，沿周向均匀分布，摩擦表面的最高温度达258.6 ℃；制动前期，制动盘表面明显上升，制动后期，制动盘表面的温度上升会趋于平缓。

b) 多次连续制动对制动盘的温度场影响比较明显，最高温度达637.5 ℃，摩擦表面温度场周向差异逐渐减小，制动盘温度场基本是轴对称分布；两次连续制动的30s冷却作用，效果明显，温度下降很快，因此实际使用时要避免连续多次制动。

c) 制动期间，随着客车的载重与制动初速度的加大，制动盘的最高温度也会随之增加，其中初速度对最高温度的影响更明显。在满足客车实际使用要求下，制动初速度和载重都要尽可能小。

[1]BELHOCINEA,BOUCHETARAM.Thermalanalysisofasoildbrakedisc[J].AppliedThermalEngineering,2012,32(6):59-67.

[2]ADAMOWICZA,GRZESP.Analysisofdiscbraketemperaturedistributionduringsinglebrakingundernon-axisymmetricload[J].AppliedThermalEngineering,2011,31(04):1003-1012.

[3]DUZGUNM.Investigationofthermo-structuralbehaviorsofdifferentventilationapplicationsonbrakediscs[J].JournalofMechanicalScienceandTechnology,2012,26(1):235-240.

[4]BELHOCINEA,BOUCHETARAM.Thermo-mechanicalmodelingofdrycontactsinautomotivediscbrake[J].InternationalJournalofThermalSciences,2012,60(16):161-170.

[5] 朱永梅，朱玉君，王新国，等.盘式制动器热结构耦合分析[J].江苏科技大学学报,2015，29(3):1673-4807.

[6] 尹安东，徐俊波，张冰战，等.电动汽车盘式制动器热-结构耦合场的分析[J].农业装备与车辆工程，2014，52(3):1673-3142.

[7] 何建成，张文明，姜勇，等.基于ABAQUS的湿式多盘制动器温度场数值模拟分析[J].矿山机械，2012，40(10):29-33.

[8] 黄健萌，高诚辉，唐旭晟，等．盘式制动器热—结构耦合的数值建模与分析[J].机械工程学报，2008，44(2):145-151.

[9] 罗庆生，韩宝玲.汽车摩擦片摩擦热分布规律的分析与研究[J].润滑与密封，2004，162(2):20-23.

[10]YEVTUSHENKOAA,GRZESP.MutualinfluenceofthevelocityandtemperatureintheaxisymmetricFEmodelofadiscbrake[J].InternationalCommunicationsinHeat&MassTransfer,2014,57:341-346.

[11] 张洪信，管殿柱.有限元基础理论与ANSYS11.0应用[M].北京：机械工业出版社，2010：66-70.

[12] 韩建荣，翁建生.盘式制动器的热分析[J].机械设计与制造，2008,12(10):180-182.

[13] 李亮，宋健，李永，等.制动器热分析的快速有限元仿真模型研究[J].系统仿真学报，2005，12(17):2869-2872.

(责任编辑： 康 锋)

The Simulation and Analysis of the Temperature Field for Passenger Car Disk Brake

LIUYan,CHENYanfeng,WUYuecheng，HUXuxiao

(Faculty of Mechanical Engineering & Automation, Zhejiang Sci-Tech University, Hangzhou 310018, China)

The research object in this paper is the brake disc of certain type bus. A brake disc 3-D model is established in Catia, then we apply HyperMesh to mesh the brake disc and conduct thermal structure coupling analysis by using Abaqus. In this paper, the heat flow density and the convection coefficient of heat transfer calculation are discussed, the single and multiple continuous braking temperature field cloud picture are compared. The temperature contours are analysised and the effects of different braking conditions of the brake disc are compared. The results show that at the end of the braking, the temperature field of friction pair has large temperature gradient along axial direction and is evenly distributed along the circumferential direction. The highest temperature is 258.6 ℃ at this time. After consecutive braking, the friction surface temperature field of circumferential difference gradually decreases, and the temperature field distribution of brake disc is basically axisymmetric. The highest temperature of brake disc increase with the initial velocity and the bus load increasing. The analysis provides a reliable basis for selecting braking conditions, choosing the disc material and improving service life.

passenger car; disk brake; coupling temperature field; finite element method

10.3969/j.issn.1673-3851.2017.05.014

2016-10-08 网络出版日期： 2017-01-19

浙江省自然科学基金一般项目(LY13E050025);浙江省自然科学基金重点项目(LZ14E050003)

刘 艳(1991-)，女，河南信阳人，硕士研究生，主要从事汽车制动系统方面的研究。

吴跃成，E-mail：wuyuecheng@126.com

U463.51+2

A

1673- 3851 (2017) 03- 0389- 05