三阶分布反馈太赫兹量子级联激光器的远场分布特性∗
朱永浩 黎华 万文坚 周涛 曹俊诚‡
1)(中国科学院上海微系统与信息技术研究所,中国科学院太赫兹固态技术重点实验室,上海 200050)2)(中国科学院大学,北京 100049)
三阶分布反馈太赫兹量子级联激光器的远场分布特性∗
朱永浩1)2)黎华1)†万文坚1)周涛1)曹俊诚1)‡
1)(中国科学院上海微系统与信息技术研究所,中国科学院太赫兹固态技术重点实验室,上海 200050)2)(中国科学院大学,北京 100049)
(2017年2月20日收到;2017年2月24日收到修改稿)
研究了三阶分布反馈太赫兹量子级联激光器的设计、制作并分析了其纵模和横模特性.通过建立波导结构模型,利用有限元方法模拟激光器波导结构内的三维模场分布,通过本征模的损耗分析器件的纵模模式选择机理.同时,由本征模的近场通过近-远场傅里叶变换求得激光器的远场分布.采用半导体工艺制作了4.3 THz双面金属波导三阶分布反馈量子级联激光器,测量了不同器件的发射谱和远场光束质量,远场发散角为12◦×13◦,实验结果和理论模拟符合.
太赫兹,量子级联激光器,单模,远场
1 引言
太赫兹(THz)波(频率0.1—10 THz,波长30µm—30 mm)介于红外光和微波之间,是整个电磁波谱中最后一个有待全面认识和研究的频段,因此THz频率也被称作“太赫兹间隙”.THz技术的发展很大程度依赖于THz辐射源和探测器的性能.目前产生THz波的电子学方法主要有:单行载流子光电二极管(UTCPD)、共振隧穿二极管(RTD)、光电导天线(PCA)[1−3]等.由于功率随频率的增大衰减严重,以上基于电子学的THz辐射源主要在1 THz以下的应用场景中展现出较大的优势.在1 THz以上且功率大于1 mW的辐射源主要依靠基于光子学的太赫兹量子级联激光器(THz QCL).自世界上第一个THz QCL[4]于2002年成功实现以来,THz QCL在输出功率和工作温度指标方面已经有了较大发展,而且在成像、通信和成谱等研究领域展现出了应用优势.另外,由于能够实现单模、可调谐、高功率等特性,THz QCL在紧凑性与灵敏性等方面具有巨大的研究价值[5,6].对于波导结构而言,已经有不同类型的结构被广泛地用于THz QCL器件研究中[7].其中半绝缘表面等离子体波导早期被广泛采用,它具有比较高的输出功率和相对比较好的光斑质量等优点[8].近年来,双面金属波导[9,10]在很多新颖的波导结构设计中被采用,因为与半绝缘等离子体波导结构相比,双面金属波导可实现近乎完美的模式限制因子.对于采用传统的法布里-珀罗(F-P)腔的双面金属波导THz QCL,由于其波导口尺寸远小于辐射光波长,所以导致器件远场光斑非常发散,几乎朝空间任何方向发射THz光子.为了解决上述问题,通常可以在双面金属波导中引入分布反馈(distributed feedback,DFB)光栅阵列或者耦合腔[11−13]来实现模式选择.基于布拉格衍射的一阶DFB光栅可实现单纵模激射,同时光从两端端面出射;二阶DFB波导结构THz QCL可实现面发射.激光器的宽度一般为几十到上百微米,即亚微米尺度,由于衍射极限的存在,其在横向有比较宽的远场发散角,所以器件的远场THz光斑一般为长条形.二维光子晶体结构THz QCL[14−16]也可以实现THz光面发射,但是通常远场光斑不是高斯分布,而且早期的光子晶体THz QCL的效率较低.而三阶DFB[17]THz QCL能够克服上述边发射与面发射激光器中的缺点,既能实现单模激射,又可以得到完美的高斯型远场光斑.对三阶DFB THz QCL而言,波导结构内纵向的相位匹配尤为重要[18].F-P腔THz QCL有效折射率大约为3.6[17],由耦合模理论可知,只有当波导中的有效折射率等于3时,一阶和二阶衍射满足行波条件耦合到空气中,三阶衍射提供反馈实现纵模的选模功能[19].
本文采用有限元方法对三阶DFB THz QCL进行了建模和模场仿真,并通过近-远场傅里叶变换研究了不同光栅占空比(8%—15%)和不同脊波导宽度(100—187µm)所对应的波导结构的远场光斑.实验结果与理论模拟符合.
2 器件仿真结构模型
本文研究的三阶DFB THz QCL结构模型与文献[17]中的结构类似,为了方便实际制作,我们对其结构做了一些调整,同时仿真的模型结构又根据结构实际效果做了一些校准,以获得最贴近实际结构的仿真效果.三阶DFB THz QCL采用双面金属波导结构,图1中黄色为上、下电极,灰色为有源区,有源区采用共振声子结构,采用GaAs/AlGaAs材料体系[20],激射波长约为70µm.光栅阵列中的有源区材料被完全刻蚀,光栅的纵向占空比为10%—15%,横向占空比为80%,光栅两侧留出的金属区域是为了保证电流分布的均匀性.上电极横向两侧分别留出脊波导总宽度的10%作为吸收边,同时在纵向的两侧分别留出100µm作为吸收边.三阶光栅一共由33个周期组成,仿真模型以第一个周期起始面底端中心处为零点,x,y,z轴的定义如图1所示.光栅阵列结构的两端分别留出两个周期长度的金属区域作为金线键合区.以脊波导的下电极平面的中心为球心建立了球坐标体系用于远场光束质量的模拟,其θ和φ方向如图1定义.

图1 (网刊彩色)三阶DFB THz QCL的三维示意图Fig.1.(color online)Three-dimensional model for third-order DFB THz QCL.
本文对DFB THz QCL波导结构的模场分析采用基于有限元计算的Comsol软件完成.由于波导中电磁场分布满足麦克斯韦方程,可以通过求解由其导出的亥姆霍兹方程得到波导中的模式分布,进而可以求得每个模式的有效折射率与近场分布.对不同的器件结构,我们主要关心其本征模的电磁场分布和损耗等信息.对于采用双面金属波导结构的THz QCL,上下金属电极的复介电常数是对模场限制的主要因素,Comsol需要根据激光器结构的每一层材料的折射率分布对其进行建模[21].器件的波导结构自下而上分别为:1µm厚的下电极(Ti/Au,20/1000 nm),50 nm厚的重掺杂层(Si,掺杂浓度为5.0×1018cm−3),10µm厚的有源区,400 nm厚的重掺杂GaAs上接触层(Si,掺杂浓度为3.0×1018cm−3).在实际仿真过程中我们将该模型简化,将上下金属层用完美导体边界条件代替.
3 基于频域的近远场变换
三阶DFB THz QCL的电磁场全部由光栅处耦合出来,由近场电磁场分布即可得到远场的光束质量,这就是场等效原理:激光器产生的电磁场可由全部光栅缝隙处的电磁场取代,通过频域的近-远场变换求得电磁场的远场分布[19].
在近-远场变换的过程中,我们通过坐标变换将图1中直角坐标系下的坐标原点平移到球坐标系下的坐标原点.令光栅缝隙处的场分布用等效表面电流和磁流(Js,Ms)表示.其中,Js=n×H=Hzx−Hxz;Ms=n×E=Ezx−Exz;n为垂直于缝隙表面的法向量;H,E分别为磁场强度、电场强度;Hx,Hz与Ex,Ez分别为H,E在直角坐标系下x,z轴方向的分量.
定义辅助矢量N,L为

其中,k为波矢;r′为由原点指向近场上的点的矢量;s′为近场截面的表面积;s为远场球面上的表面积;Jx,Jy,Jz和Mx,My,Mz分别为Js,Ms在直角坐标系下x,y,z轴方向的分量.
将N,L变换到球坐标系中可得

其中,Nθ,Nφ和Lθ,Lφ分别为N,L在球坐标系下θ和φ方向的分量.再利用辅助位函数法,定义频域位函数A,F

其中,ε0,µ0分别为真空介电常数与真空磁导率;r为由原点指向远场上的点的矢量;R=r−r′,在(3)式中我们取了近似:

电磁场由频域位函数表示为

其中,ω为器件激射角频率.由(3)式中(A,F)与(N,L)的关系,(E,H)可由(N,L)表示.在远场区域电磁场的球坐标系下的各个场分量为


其中,Er,Eθ,Eφ和Hr,Hθ,Hφ分别为E,H在球坐标系下r,θ,φ方向的分量;Aθ,Aφ和Fθ,Fφ分别为A,F在球坐标系下θ,φ方向的分量;辐射强度可由辅助矢量的球坐标系分量表示:

其中,K为辐射强度,P为波印廷矢量,Pr为P在r方向的分量,Ω为立体角.
对于三阶DFB,在近场截面只有Ex,Hz分量,其余分量为0,本文中计算所用的近场截取的平面在光栅缝隙上端面上方0.1µm处,采集精度为1µm.
4 不同占空比光栅的远场仿真结果
图2为对三阶THz QCL的远场仿真的结果,我们在保证器件的本征频率不变的情况下,调整光栅的占空比从8%—15%,对应的波导有效折射率从3.2675降到3.061,由于有效折射率越来越接近相位匹配条件neff=3,仿真求得的远场光斑从发散到会聚于中心的紧凑的光斑.同时,在这个变化过程中谐振频率的模式损耗从14.629 cm−1增加到17.99 cm−1.由于波导中的有效折射率不断接近3,其耦合系数也在不断增加,在一定程度上能够弥补增加的模式损耗.仿真结果表明可以通过改变光栅的占空比来调节波导中有效折射率以获得相位匹配条件,从而提高器件远场光斑质量.
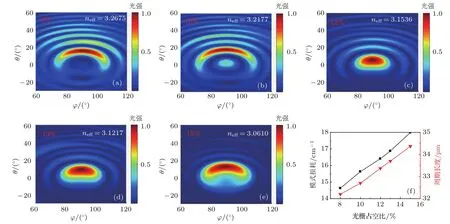
图2 (网刊彩色)(a)—(e)不同纵向占空比光栅的三阶 DFB THz QCL远场计算结果;(f)为对应的周期长度与模式损耗的变化情况;器件模型采用实际测得的结构参数,仿真假设光栅处有源区全部都被刻蚀,设计的本征频率为4.27 THzFig.2.(color online)(a)–(e)Simulated far- fi eld patterns of the 3rd-order DFB THz QCLs with di ff erent grating duty cycles;(f)the calculated mode loss and period length as a function of the grating duty cycle for a given designed frequency of 4.27 THz.The dimensions used in calculations are obtained from microscope measurements.We assume the active region in the grating apertures are completely etched away.
5 器件的制作与实验方法
本文中制作三阶DFB THz QCL的有源区材料采用GaAs/AlGaAs材料体系,由分子束外延生长得到.首先在THz QCL晶圆和n型GaAs衬底上磁控溅射键合金属(Ti/Au,20/500 nm),然后在高温高压下进行Au-Au晶片键合.通过对键合后的晶圆材料进行机械减薄和湿法腐蚀去除半绝缘GaAs衬底,然后将其浸泡在40%浓度的氢氟酸(HF)中10 s将腐蚀阻挡层清洗干净,再用H3PO4:H2O2:H2O为1:1:25的溶液将上接触层从400 nm减到200 nm从而降低器件的损耗.通过光刻、电子束蒸发、剥离等步骤制作Ti/Au(20/350 nm)上电极[22].然后通过感应耦合等离子体化学汽相淀积在120◦C的温度下生长一层1.5µm的Si3N4做干法刻蚀掩模.通过光刻将整个脊波导部分用光刻胶保护起来,将晶圆放入反应离子刻蚀(reactive ion etching,RIE)机中对Si3N4开窗口,刻蚀气体为CF4,将暴露在外的Si3N4刻蚀至400 nm,然后将残余的光刻胶清洗干净.再通过光刻将光栅暴露出来,再次放入RIE机中,将光栅暴露的Si3N4完全刻蚀,然后将晶圆放入感应耦合等离子刻蚀机(Oxford 180)中实现GaAs半导体刻蚀,干法刻蚀的气体采用Cl2和Ar2,为了获得相对光滑的侧壁,选择刻蚀温度为45◦C.由于光栅的最小线宽约为3µm,在刻蚀的过程中光栅内材料的刻蚀速率偏慢,下电极上方残留的400 nm Si3N4能够保证在过刻过程中下电极处的金不被轰击到波导侧壁上,避免造成器件短路.图3为干法刻蚀后清洗干净的三阶DFB THz QCL芯片.为了提高器件的热特性,我们采用机械研磨的方法将n型GaAs衬底磨薄至150µm,磁控溅射背面电极(Ti/Au,20/200 nm).最后解离的激光器管芯通过铟片焊接在铜热沉上,采用金丝焊线实现电注入.封装好的器件被安装在热控冷头中以实现低温工作环境.THz光从聚乙烯窗片辐射到自由空间,光强采用高莱(Golay Cell)探测器测量.远场测试中Golay Cell探头在距离激光器出射端面10 cm处的球面上,θ与φ的取向与图1中的相同.THz QCL的激射光谱由Bruker VERTEX 80/80v远红外傅里叶变换光谱仪测量,采用安捷伦8114A和AVTECH脉冲电源对器件进行供电.

图3 制作的三阶DFB THz QCL的扫描电子显微镜(SEM)照片Fig.3.SEM image of the fabricated third-order THz QCL.
6 仿真与实验结果对比
本文主要研究分析了两种不同宽度的器件,较宽器件类型标记为W,较窄器件类型标记为N.实际制作的器件周期长度与设计长度一致,根据对光栅干法刻蚀的实际不同宽度与深度研究了W的两个器件W-1与W-2.
为了计算不同DFB结构的不同模式的模式损耗,我们根据实际测得的结构参数对器件进行了三维有限元仿真. 器件本征模的频率由f=3c/(2neffΛ)决定,c为光速,neff为波导的有效折射率,Λ为周期长度.对于器件W,我们设计脊波导总宽度为187µm,周期长度为32.7µm,其中光栅的占空比为10%,对应的谐振频率为4.25 THz.图4(a)为器件W-1实际波导结构的侧面解理面的SEM图,其中光栅刻蚀深度大约为6µm,光栅实际占空比为10%,考虑到不同的刻蚀深度将影响波导结构的有效折射率,我们用等效折射率法计算光栅处的有效折射率.图4(b)为仿真得到的器件W-1的模式损耗分布图,中间有0.3 THz的光子能带带隙.在带隙右侧的模式通常都散逸到空气中,因此具有更大的模式损耗.对于带隙左侧的模式,大部分被限制在上下电极之间,因而有更高的模式限制因子、具有更小的模式损耗、更容易在波导腔中传播.仿真得到的器件W-1波导结构的本征频率为4.1702 THz,对应的模式损耗为14.36 cm−1.图4(c)和图4(d)分别为仿真的低损耗本征模(4.1702 THz)和高阶横模(4.2447 THz)在腔内的Ey分量,本征模电场能量更加集中在波导结构的中心位置而高阶横模的Ey分量则分散为两束纵向电场.由于光栅未能刻蚀到下电极而导致频率向下偏移约80 GHz.对于器件W-2,其实际测得的刻蚀深度为9µm,光栅的实际占空比约为12%,仿真得到的本征频率为4.34 THz.

图4 (网刊彩色)(a)沿纵向(x方向)解理之后器件W-1的SEM图;(b)模拟计算得到的器件W-1本征频率的损耗;(c)最低损耗的本征模的电场(Ey)分布图;(d)高阶横模的电场Ey分布图Fig.4.(color online)(a)SEM image of the fabricated sample cleaved along the x-axis;(b)the simulated mode losses for eigen modes of device W-1;(c)Eydistribution of the eigen mode with the lowest loss;(d)Eydistribution of the higher-order lateral mode.
对于器件N,其结构与器件W类似,但是脊波导宽度为100µm.设计的频率和光栅占空比分别为4.25 THz,8%.由于脊波导设计的占空比相对器件W-1减少,为了保持谐振频率不变,设计周期长度减小至32.2µm.实际测得的光栅的占空比为12%,刻蚀深度为9µm.图5(a)是对实际器件N建模计算得到的本征模模式损耗,损耗最小的本征模的频率为4.4188 THz,红色标记的为高阶横模.由于光栅的实际占空比的增加,对其仿真得到的谐振频率比设计的谐振频率向上偏移0.17 THz.图5(b)为器件N在谐振频率处电场的Ey分量,与图4(d)相比,器件N在该本征频率处电场分布更加集中,预期远场光束质量应该更好.在图8中,我们会详细分析其远场光束质量.
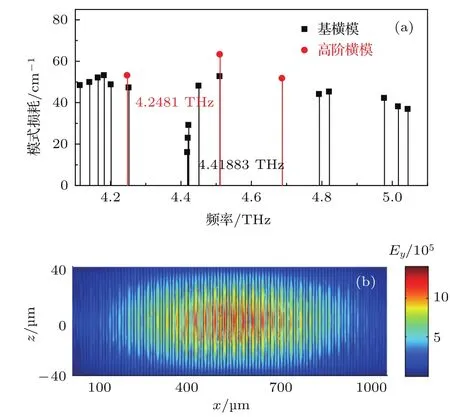
图5 (网刊彩色)(a)模拟计算得到的不同本征模式的损耗;(b)器件N在本征频率4.4189 THz处波导腔内的Ey分布Fig.5.(color online)(a)Simulated mode losses for di ff erent eigen frequencies;(b)Eydistribution at the eigen frequency with the lowest mode loss.
图6为器件W-1,W-2,N三个器件在脉冲模式下的功率-电流-电压(L-I-V)特性.脉冲电源重复频率为10 kHz,三个器件的电脉冲宽度分别为12.8,1.0,3.3µs,对应12.8%,1.0%,3.3%的电脉冲占空比.测量得到的器件W-1,W-2,N的阈值电流密度Jth分别为462.2,622.2,728.6 A/cm2,其阈值电流密度的差异是由不同光栅结构引起的模式损耗的不同而导致的.插图为每个器件在最大光强输出时的发射谱.器件W-1,W-2,N激射谱对应的峰值频点分别为4.0,4.27,4.385 THz,器件W-2与N均存在一个多模.

图6 (网刊彩色)实验测量得到的三个不同三阶DFB THz QCL的L-I-V特性,插图为每个器件对应的THz发射谱Fig.6.(color online)L-I-V characteristics of the three third-order DFB THz QCLs measured in pulsed mode.The inset shows the emission spectra for the three devices.
为了研究波导结构中不同有效折射率对器件远场光斑的影响,我们分别从仿真与测试两方面对不同器件的远场做了对比.作为参考,我们测量了F-P腔双面金属波导器件的远场光束质量,如图7所示.与预期一样,双面金属波导F-P腔THz QCL的远场光束质量很差,几乎朝空间任意方向辐射THz光子.图8(a)、图8(c)和图8(e)为采用傅里叶变换方法计算得到的三阶DFB器件W-1,W-2和N的远场分布图.可以看到图8(a)比较发散,图8(b)、图8(d)和图8(f)分别为对器件W-1,W-2与N的实际测试得到的远场图,表1包含三个器件的光栅占空比、仿真得到的本征频率、测试得到的激射谱峰值频率、激射谱峰值频率对应的有效折射率、测得的远场发散角等信息.对于器件W-1,可以看到图8(a)比较发散,能量更多地集中在衍射环上,其发散角也比较大.实际测得的远场光斑形貌也比较发散,光强分布于多个光斑,远场分布与理论计算差别较大.由器件W-1峰值激射谱对应的频率算得有效折射率为3.44,与相位匹配所需的有效折射率均相距甚远.我们认为这种激射模式相位不匹配是导致远场发散角大的主要原因.至于实验测量的远场表现为多个光斑,依据当前的模拟结果,很难做出精确解释.对于器件W-2,测得其在θ和φ方向的远场发散角分别为14.5◦,13.5◦,光斑与仿真结果图8(c)相比形貌相近,不过在φ方向收窄,可能与器件波导宽度较宽有关.激射谱峰值频率对应的有效折射率为3.22.图8(f)为测得的器件N的远场光斑图,相比器件W-1的测试结果,器件N的远场光斑更加聚集在光斑中心处,θ和φ方向的发散角分别为12◦,13◦,光斑两侧的衍射环非常微弱,能量主要集中在中心光斑上.通过比较理论计算(图8(e))和实验测量的远场光斑,我们发现在图8(f)中除了中心高能量光斑之外,在其右上方位还出现了一个弱的光斑.根据分析,这个弱光斑可能是由于反射造成的.三阶DFB THz QCL的远场光斑分布在器件的两端,由于在器件内侧一端用于引线的陶瓷片会造成THz光反射,所以我们测得两个光斑,如图8(f)所示.测得的光谱频率对应于4.3858 THz,该频率对应的波导有效折射率为3.19,其相位匹配效果较好.

图7 (网刊彩色)F-P腔THz QCL的远场光斑图Fig.7. (color online)Far- fi eld pattern of a double metal THz QCL with a F-P cavity.

图8 (网刊彩色)(a),(c),(e)分别为对器件W-1,W-2和N仿真得到的远场分布图;(b),(d),(f)分别为器件W-1,W-2和N实验测试得到的远场分布图Fig.8.(color online)Panels(a),(c),(e)are simulated far- fi eld patterns;panels(b),(d),(f)are measured far- fi eld patterns.

表1 三阶DFB THz QCL器件各参数比较Table 1.The quantities,grating duty cycle,eigen frequency,measured lasing frequency,corresponded e ff ective refractive index of the measured peak lasing frequency and far- fi eld divergent angles,of the investigated third-order DFB THz QCLs.Note that in the“lasing frequency” column,the number in bracket represents the frequency of the secondary longitudinal mode.
由上述讨论可知,对三阶DFB THz QCL而言,其相位匹配条件neff=3对器件的光束质量尤为重要.若波导的有效折射率neff>3,neff越大,波导结构可设计的最大光栅阵列周期数就越小,我们可通过改变光栅的占空比来降低波导的有效折射率.对于周期数不是很多的器件,neff能够在大于3的同时保证远场光束的质量,因此我们可以根据设计的器件周期数在12%—15%的范围内调整合适的光栅占空比.
7 结 论
本文给出了在双面金属波导中引入三阶DFB光栅改善THz QCL远场光斑的方法.通过对结构的仿真,提出了通过改变光栅的占空比解决三阶DFB光栅中存在的相位不匹配的方案,使波导的有效折射率neff接近3.实验中测得远场光斑在θ和φ方向的半高宽为12◦×13◦.后续工作中我们将继续改善器件制作工艺,提高干法刻蚀的精度和光栅侧壁的光滑度.
[1]Song H J,Ajito K,Mumoto Y,Wakatsuki A,Nagatsua T,Kukutsu N 2012Electron.Lett.48 953
当抛光液中FAOA的体积分数增至5 mL/L时,CMP后的晶圆缺陷最少(约为896个)。继续增大抛光液中FAOA的体积分数,缺陷数量反而略升。这是因为当溶液中的表面活性剂浓度达到一定之后,其对硅溶胶及铜表面的包裹覆盖能力达到极限。过多的表面活性剂将令抛光液产生大量泡沫,泡沫表面的硅溶胶容易产生结晶,这些硅溶胶结晶也会刮伤晶圆表面。
[2]Asada M,Suzuki S,Kishimoto N 2008Jpn.J.Appl.Phys.47 4375
[3]Ropagnol X,Khorasaninejad M,Raeiszadeh M,Safavi-Naeini S,Bouvier N,Côté C Y,Laramée A,Reid M,Gauthier M A,Ozaki T 2016Opt.Express24 11299
[4]Köhler R,Tredicucci A,Beltram F,Beere H E,Lin fi eld E H,Davies A G,Ritchie D A,Lotti R C,Rossi F 2002Nature417 156
[5]Borri S,Patimisco P,Sampaolo A,Beere H E,Ritchie D A,Vitiello M S,Scamarcio G,Spagnolo V 2013Appl.Phys.Lett.103 021105
[6]Vitiello M S,Consolino L,Bartalini S,Taschin A,Tredicucci A,Inguscio M,Natale P D 2012Nat.Photon.6 525
[7]Kumar S 2011IEEE J.Sel.Top.Quant.17 38
[8]Wienold M,Röben B,Schrottke L,Sharma R,Tahraoui A,Biermann K,Grahn H T 2014Opt.Express22 3334
[9]Williams B S,Kumar S,Callebaut H,Hu Q,Reno J L 2003Appl.Phys.Lett.83 2124
[10]Li H,Cao J C,Tan Z Y,Feng S L 2008J.Appl.Phys.104 103101
[11]Wienold M,Tahraoui A,Schrottke L,Sharma R,Lü X,Biermann K,Hey R,Grahn H T 2012Opt.Express20 11207
[12]Kumar S,Williams B S,Qin Q,Lee A W M,Hu Q 2007Opt.Express15 113
[13]Li H,Manceau J M,Andronico A,Jagtap V,Sirtori C,Li L H,Lin fi eld E H,Davies A G,Barbieri S 2014Appl.Phys.Lett.104 241102
[14]Benz A,Fasching G,Deutsch C,Andrews A M,Unterrainer K,Klang P,Schrenk W,Strasser G 2007Opt.Express15 12418
[15]Liang G Z,Liang H K,Zhang Y,Khanna S P,Li L H,Davies A G,Lin fi eld E,Lim D F,Tan C S,Yu S F,Liu H C,Wang Q J 2013Appl.Phys.Lett.102 031119
[16]Xu G Y,Colombelli R,Khanna S P,Belarouci A,Letartre X,Li L H,Lin fi eld E H,Davies A G,Beere H E,Ritchie D A 2012Nat.Commun.3 952
[17]Amanti M I,Fischer M,Scalari G,Beck M,Faist J 2009Nat.Photon.3 586
[18]Cui M,Hovenier J N,Ren Y,Vercruyssen N,Gao J R,Kao T Y,Hu Q,Reno J L 2013Appl.Phys.Lett.102 111113
[19]Amanti M I 2010Ph.D.Dissertation(Napoli:Università degli Studi di Napoli Federico II)
[20]Williams B S,Kumar S,Hu Q,Reno J L 2006Electron.Lett.42 89
[21]Xu T H,Yao C,Wan W J,Zhu Y H,Cao J C 2015Acta Phys.Sin.64 224212(in Chinese)[徐天鸿,姚辰,万文坚,朱永浩,曹俊诚2015物理学报64 224212]
[22]Wan W J,Yin R,Tan Z Y,Wang F,Han Y J,Cao J C 2013Acta Phys.Sin.62 210701(in Chinese)[万文坚,尹嵘,谭智勇,王丰,韩英军,曹俊诚2013物理学报62 210701]
PACS:95.85.Gn,42.55.Px,42.25.Bs,42.60.JfDOI:10.7498/aps.66.099501
Far- fi eld analysis of third-order distributed feedback terahertz quantum cascade lasers∗
Zhu Yong-Hao1)2)Li Hua1)†Wan Wen-Jian1)Zhou Tao1)Cao Jun-Cheng1)‡
1)(Key Laboratory of Terahertz Solid-State Technology,Shanghai Institute of Microsystem and Information Technology,
Chinese Academy of Sciences,Shanghai 200050,China)2)(University of Chinese Academy of Sciences,Beijing 100049,China)
20 February 2017;revised manuscript
24 February 2017)
The single lobe far- fi eld patterns produced from terahertz quantum cascade lasers(QCLs)are greatly demanded for various applications,such as imaging,data transmission,etc.However,for a ridge waveguide terahertz QCL,the farfi eld beam divergence is large due to the fact that the waveguide aperture is far smaller than the terahertz wavelength.This is the case typically for double-metal waveguide terahertz QCL which emits terahertz photons in almost every direction in the space.Even for a single plasmon waveguide terahertz QCL,the divergence angle is as large as 30◦in both horizontal and vertical direction.Here,in this work we design and fabricate a double metal third-order distributed feedback terahertz QCL emitting around 4.3 THz,and investigate the characteristics of the longitudinal and transverse modes.This work aims to achieve high beam quality for terahertz QCL by exploiting the third-order distributed feedback geometry,and in the meantime to achieve single longitudinal mode operation.The electromagnetic fi eld distribution in the waveguide is modelled by employing a fi nite element method.The mode selection mechanism is studied by using the eigen frequency analysis,and the far- fi eld beam is simulated by applying the near- fi eld to far- fi eld Fourier transform technique.The QCL active region used in this work is based on the resonant-phonon design,which is grown by a molecular beam epitaxy(MBE)system on a semi-insulating GaAs(100)substrate.The wafer bonding and traditional semiconductor device fabrication technology,i.e.,optical lithography,electron beam evaporation,lift-o ff,wet and dry etching,are used to process the MBE-growth wafer into the third-order distributed feedback geometry with double-metal waveguides.By carefully designing the grating structures and optimizing the fabrication process,we achieve third-order distributed feedback terahertz QCL with quasi-single-longitudinal mode operation and single lobe far- fi eld beam pattern with low beam divergence in both vertical and horizontal directions.The e ff ect of grating duty cycle on the far- fi eld beam divergence is systematically studied theoretically and experimentally.By the simulation,we fi nally achieve the divergence angle of 12◦×13◦for a third-order distributed feedback laser with a grating duty cycle of 12%that results in an e ff ective refractive index close to 3.The experimental results show good agreement with the simulation.There is still room to further reduce the beam divergence of third-order distributed feedback terahertz QCL by improve the accuracy of the simulation and the fabrication.
terahertz,quantum cascade laser,single mode,far fi eld
10.7498/aps.66.099501
∗中国科学院“百人计划”、国家重点基础研究发展计划(批准号:2014CB339803)、国家重大科学仪器设备开发专项(批准号:2011YQ150021)、国家自然科学基金(批准号:61575214,61404149,61404150,61604161)和上海市科学技术委员会(批准号:14530711300,15560722000,14ZR1447400,15YF1414400,15JC1403800)资助的课题.
†通信作者.E-mail:hua.li@mail.sim.ac.cn
‡通信作者.E-mail:jccao@mail.sim.ac.cn
*Project supported by the“Hundred-Talent” Program of Chinese Academy of Sciences,the National Basic Research Program of China(Grant No.2014CB339803),the Major National Development Project of Scienti fi c Instrument and Equipment of China(Grant No.2011YQ150021),the National Natural Science Foundation of China(Grant Nos.61575214,61404149,61404150,61604161),and the Shanghai Municipal Commission of Science and Technology,China(Grant Nos.14530711300,15560722000,14ZR1447400,15YF1414400,15JC1403800).
†Corresponding author.E-mail:hua.li@mail.sim.ac.cn
‡Corresponding author.E-mail:jccao@mail.sim.ac.cn

