以团簇加连接原子模型解析Cr-C共晶成分∗

王同 胡小刚 吴爱民 林国强 于学文 董闯†

1)(大连理工大学,三束材料改性教育部重点实验室,大连 116024)2)(大连纳晶科技有限公司,大连 116600)

以团簇加连接原子模型解析Cr-C共晶成分∗

王同1)胡小刚1)2)吴爱民1)林国强1)于学文2)董闯1)†

1)(大连理工大学,三束材料改性教育部重点实验室,大连 116024)2)(大连纳晶科技有限公司,大连 116600)

(2016年11月9日收到;2017年2月3日收到修改稿)

Cr-C体系材料是重要硬质防护涂层的代表,具有共晶特征.我们的前期工作指出,共晶合金满足双团簇近程序结构模型,由两种稳定液体亚单元构成,各自满足理想非晶团簇成分式,这里的第一近邻团簇来自相关共晶相.显然共晶成分解析的关键在于获得团簇,而相结构中往往存在多种团簇,进入到非晶/共晶团簇成分式的主团簇定义是关键环节.本文通过应用Friedel振荡理论及原子密堆,以团簇分布的球周期性及孤立度为判据,以Cr-C共晶相为例,进一步细化了共晶相中的主团簇选择流程,再搭配以2,4或6个连接原子,获得了描述共晶成分Cr86C14和Cr67.4C32.6的双团簇成分式:[Cr-Cr14+C-Cr9]CrC3和[C-Cr9+C-Cr8]C6,其中四种团簇分别来自共晶相Cr,Cr23C6,Cr7C3和Cr3C2.该工作进一步证实了团簇加连接原子模型在共晶点解析中的普适性,并从理论上支持了相关的材料设计.

Cr-C,团簇加连接原子模型,共晶点,主团簇

1 引 言

广泛使用的硬质防护涂层主要为金属与类金属体系,而其中过渡金属与C的体系几乎都呈现共晶特征,例如Cr-C体系含有两个共晶点Cr86C14和Cr67.4C32.6,所有Cr-C化合物均为共晶相,常用的硬质防护涂层为化合物晶体相和富C端的Cr掺杂非晶C.CrC就是一种广泛使用的有金属色泽的防护涂层,具有很好的力学性能及化学稳定性［1].掺Cr的非晶态C(常称为掺杂类金刚石,Cr-DLC)涂层材料摩擦性能较好［2],同时具有高抗腐蚀性和高导电性,有望用于质子交换燃料电池双极板涂层中［3,4].

共晶合金的特征在于由两相构成,且具有明确的成分点.长期以来,人们曾提出各种液态结构模型,试图理解其结构和成分根源［5−13],其核心在于认为原子间呈现化学及拓扑短程序结构特征,尤其强调第一近邻配位多面体团簇的作用.例如,共晶液体Ni81B19与Au81Si19中均存在着二十面体团簇［9,13].另外,根据第一性原理模拟,Fe83B17共晶熔体结构以类面心或二十面体团簇为结构特征［6].尽管人们普遍认为共晶成分的根源在于近程序结构特征,但上述结构描述均无法给出共晶成分的定量解释.

我们发展的团簇加连接原子结构模型适用于描述合金近程序的结构特征,成功地应用于高非晶形成能力的块体非晶合金成分的定量解析［14],在此基础上,建立了双团簇共晶熔体模型,即共晶体由两个稳定熔体构成,分别对应于两种共晶相,并各自均满足理想非晶的团簇成分式,共晶成分因此可以由双团簇成分式[clusterα+clusterβ](glue atoms)2or4or6表示,这里的两种团簇分别源自两个共晶相,连接原子的个数按照每个单独团簇成分式分别为1或3来计算.该理论已经在B-过渡金属共晶成分解析中得到了验证,如Cr-B体系中富Cr共晶成分解析结果为Cr86.5B13.5≈[Cr-Cr14+BB2Cr8]Cr3B,其中团簇[Cr-Cr14](以Cr为心的配位数为14的体心立方团簇)和[B-B2Cr8](以硼为心的配位数为10的阿基米德反棱柱)分别来自共晶相BCC-Cr和BCr2(Al2Cu结构)［15].

由于共晶成分已经广泛测定,我们的解析方法能精确得到两种稳定熔体的团簇成分式,在某些特定情形下,稳定熔体等效于高非晶形成能力,这使定量理解和设计非晶合金成为可能,而共晶点的解析则是非晶材料设计的关键步骤.

下面首先简要介绍团簇加连接原子结构模型,然后把该模型应用于Cr-C体系共晶点的解析.

2 团簇加连接原子模型

传统晶体学以晶胞作为基本单元,用原子位置及空间群来描述固态物质的微观原子排布,仅适用于描述具有简单晶体结构的合金相,而不能精准地理解结构复杂的合金相、玻璃态合金及准晶体的结构特征.Dong等［14]基于对非晶、准晶的研究成果,提出了团簇加连接原子模型,即以团簇成分式“[团簇](连接原子)”描述非晶合金中原子排布的近程序结构.该模型利用团簇式描述复杂合金相,突破了传统晶体学中原子周期性重复排列的制约.

团簇加连接原子模型是由中心原子、壳层原子以及连接原子构成,其中,壳层原子紧绕中心原子排布,连接原子依次分布于第二及以上近邻的壳层上.图1为该模型的平面示意图,其中深灰色圆代表中心原子,白色圆代表壳层原子,浅灰色圆代表连接原子.该模型中,团簇是描述合金体系中原子局域堆垛的第一近邻配位多面体,团簇式是由团簇加若干个连接原子组成,连接原子的个数取决于团簇的排列方式.具有高非晶形成能力的非晶合金,其团簇式的连接原子个数为1或3［16].基于共晶液体由两种高非晶形成能力的稳定熔体等比例构成的假设上,每种稳定熔体均可由非晶团簇式描述.由两种团簇搭配2,4或6个连接原子构成的双团簇式,作为共晶点成分式,即可对共晶成分进行解析.其中,两种团簇分别来自于两种共晶相,是以团簇分布的球周期性及其孤立度为准则选取的最能反映合金相短程有序结构特征的团簇基元［17].图1中,r1为团簇的中心原子到第一近邻壳层原子的平均半径,r3为相邻团簇中心原子之间的距离,即团簇间距,且r3=2.6r1.

图1 团簇加连接原子模型的平面示意图(r1为团簇的中心原子到第一近邻壳层原子的平均半径,r3代表相邻团簇中心原子之间的距离,且r3=2.6r1)Fig.1. Schematic presentation of the cluster-plusglue-atom model.The numerical relationship between basic cluster radius(r1)and cluster distance(r3)is r3=2.6r1.

3 共晶成分解析方法

按照我们前期的工作,共晶合金由两种稳定熔体构成,分别对应于两种共晶相,且每种稳定熔体的结构单元可由形如“[团簇](连接原子)1或3”的团簇式描述.这里的核心成分解析步骤在于确定两种团簇.由于共晶相一般含有多个局域团簇结构,而最终只有一种称为主团簇的进入相应的理想非晶团簇成分式,需要引入相应的判据,定义该主团簇.Ma等［15]侧重团簇基元的密堆性及孤立度,用真实团簇中心原子半径R0与壳层原子半径R1的比率表示团簇的密堆率,即Rcluster=R0/R1,团簇共享后的有效原子个数与团簇总的原子个数比值表示团簇的孤立度,把Rcluster最接近于R∗［18](R∗为中心溶质原子与壳层溶剂原子理想密堆时的配位数对应的原子半径比)且孤立度最高的团簇单元定义为合金相的主团簇.以共晶成分两侧合金相的主团簇搭配2,4或6个连接原子成功解析了硼与过渡金属的共晶成分.但该方法在确定第一近邻上存在模糊之处,另外,由于原子并非具有确定半径的刚性球体,会导致孤立度的几何计算方法失准.Dong等［19]在Friedel振荡理论的基础上,证实了团簇中心原子到最外层原子的距离rL与其到最内层原子的距离rS存在着上限比率关系,即rL/rS=1.5;通过分析相结构中大小原子的半径比RL/RS与外层原子覆盖在内层表面的形状,在保证团簇密堆的情况下,即可确定团簇半径的截断距离,给出了准确的团簇定义方法.此外,Dong等［19]还揭示了Friedel振荡所引起的团簇分布的球周期性,通过对比总原子密度径向分布与理想有效对势函数分布情况,选出能进入描述相关稳定熔体成分式的团簇,进一步完善了主团簇的定义规则［17].但该方法在主团簇的定义上弱化了团簇密堆率的影响,使得在团簇球周期性及其孤立度差别较小的情况下,无法精准地定义出合适的主团簇.

本文兼顾前期工作中的优缺点,首先精确定义了共晶相中的第一近邻团簇,然后从中选取了主团簇,其主要依据为Friedel振荡理论及团簇密堆,通过确定相结构中大小原子的半径比RCr/RC,分析外层原子覆盖在内层表面的形状,即可定义Cr,Cr23C6,Cr7C3和Cr3C2的团簇基元;以团簇分布的球周期性及其孤立度为准则,并兼顾团簇密堆率,选取总原子密度径向分布与理想有效对势函数分布最接近共振状态,团簇中心原子到与其具有相同占位的最近邻原子的距离最接近团簇间距r3,且密堆率较大的团簇作为最能反映短程有序结构特征的主团簇;将共晶成分两侧合金相的主团簇搭配2,4或6个连接原子即可得到描述共晶成分的双团簇成分式.通过实施上述规则,解决了主团簇定义难题,从而将双团簇模型引入Cr-C体系,完成了共晶成分Cr86C14和Cr67.4C32.6的解析.

下面从第一近邻团簇定义、主团簇确定两个方面详细阐述双团簇成分式的建立过程.

3.1定义第一近邻团簇

团簇是合金相中原子局域堆垛的第一近邻配位多面体结构,根据Friedel振荡理论及团簇密堆原则即可确定团簇半径的截断距离［19],定义出团簇基元的结构类型.Friedel振荡理论指出,在电子对外加杂质电荷的不完全屏蔽作用下,费米气体或费米液体中的杂质缺陷会引起金属或半导体系统中局部电荷的扰动,使得杂质电荷周围的电子重新分布,从而产生其密度的振荡［20].对于液体和金属玻璃,Friedel振荡势函数Φ(r)∝ cos(2kFr+θ)/r3会发生π/2的相偏移,变形可知Φ(r)∝ −sin(2kFr)/r3［21].这里,kF为费米波矢,θ为相位移,r则是任意位置到中心原子的距离.该函数的系列零点呈现球周期分布,分别对应于团簇壳层原子的分布区域,且其第一个波谷限定了团簇第一近邻的分布范围.前期工作中,Dong等［19]已证实了团簇中心原子到最外层原子的距离rL与其到最内层原子的距离rS存在着确定的上限比率关系,即rL/rS=1.5.此外,团簇密堆原则［18]指出,可通过比对相结构中大小原子的半径比RL/RS,分析外层原子覆盖在内层表面的形状,定义出密堆度最大的团簇基元.团簇密堆原则不仅能减少系统的热力学自由体积和总能量,使系统的结构趋于稳定状态;而且能够提高合金熔体的黏性,不利于原子的重新排列,抑制了与之相竞争的晶体相的形核和长大.

如图2所示,Cr-C体系中有两个共晶点,分别为Cr86C14和Cr67.4C32.6,共晶成分两侧的合金相分别为Cr,Cr23C6,Cr7C3和Cr3C2.按照如下步骤,定义出以合金相中不同原子占位为心的第一近邻团簇.

1)确定体系中两种原子的半径比值:这里RCr=0.128 nm,RC=0.092 nm,两种原子半径比值RCr/RC约为1.39.

2)从Pearson手册中查询各合金相的信息［22],表1为Cr23C6相的结构信息,该相具有五个非等效的原子占位,分别为Cr1,Cr2,C,Cr3和Cr4,上标数字表示相同原子占位次序,其结构类型、Pearson符号、空间群以及序号分别为Cr23C6,cF116,和225.

表1 Pearson手册中Cr23C6相的结构数据Table 1.Structural data for Cr23C6phase taken from Pearson’s Handbook.

图2 (网刊彩色)Cr-C体系共晶成分Cr86C14和Cr67.4C32.6的双团簇成分式[Cr-Cr14+C-Cr9]C3Cr和[CCr9+C-Cr8]C6,其中四种团簇分别来自Cr,Cr23C6,Cr7C3和Cr3C2Fig.2.(color online)Interpretation of Cr86C14and Cr67.4C32.6eutectic points using a dual-cluster formula.For Cr86C14and Cr67.4C32.6eutectic points,two clusters being derived from eutectic phases Cr and Cr23C6,Cr7C3and Cr3C2respectively.

3)利用晶体学软件(例如Diamond)输出合金相的原子结构,获得以不同原子占位为心的近邻原子排布情况.例如,在Cr23C6相中,将C原子作为中心原子,有4个等距原子Cr3分布于C原子最近邻壳层处,键长为0.21121 nm;次近邻为4个等距Cr4原子,与C原子之间的键长为0.21301 nm;第三近邻处排布着1个Cr1原子,与C原子之间的键长为0.29324 nm.

4)定义以合金相中不同原子占位为心的团簇.将定义团簇的方法应用于Cr23C6合金相,RCr/RC≈1.39,以C原子作为中心原子,得到rS=0.21121 nm,则团簇截断距离的上限值rL=1.5×rS=0.316815 nm.中心C原子与距其0.21301 nm内的壳层原子(4个等距原子Cr3和4个等距原子Cr3)构成由8个三角形和2个正方形包裹的多面体;加上距其0.29324 nm的1个Cr1原子,即可构成由4个三角形覆盖在内层正方形的CN9立方多面体;再加上下一壳层的4个C原子构成CN13立方多面体.考虑到该壳层原子与中心原子的距离0.33903 nm大于团簇截断距离的上限值,因此定义[C-Cr9]为Cr23C6相中以C原子为心的团簇.同样地,可获得该相中以不同原子占位为心的五个团簇,分别为[Cr-Cr12C6],[Cr-Cr16],[C-Cr9],[Cr-C3Cr10]和[Cr-C2Cr12],结果如表2所列.另外,表3和表4列出了Cr7C3相和Cr3C2相中以不同原子占位为心的第一近邻结构及其图示.

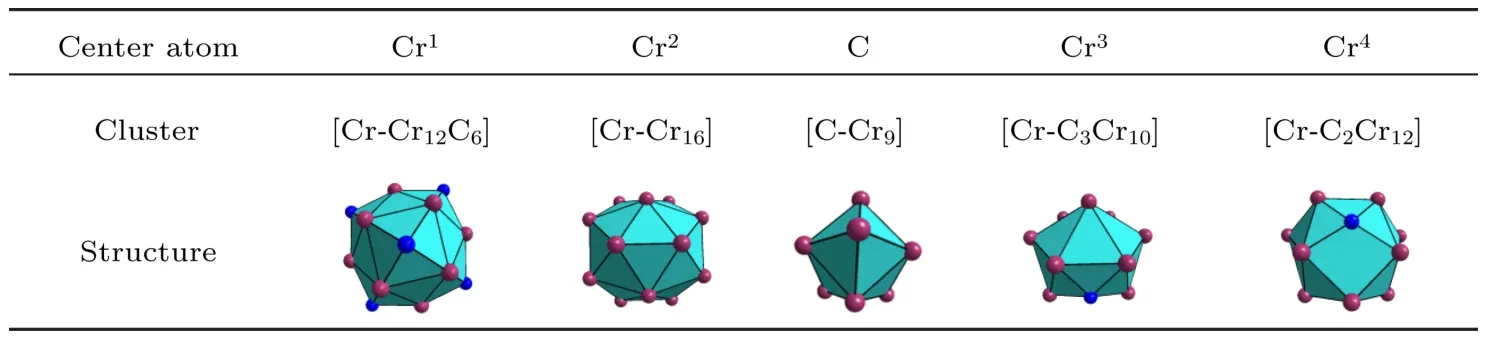
表2 (网刊彩色)Cr23C6相不同原子占位对应的团簇Table 2.(color online)Clusters centered by di ff erent non-equivalent sites in Cr23C6.

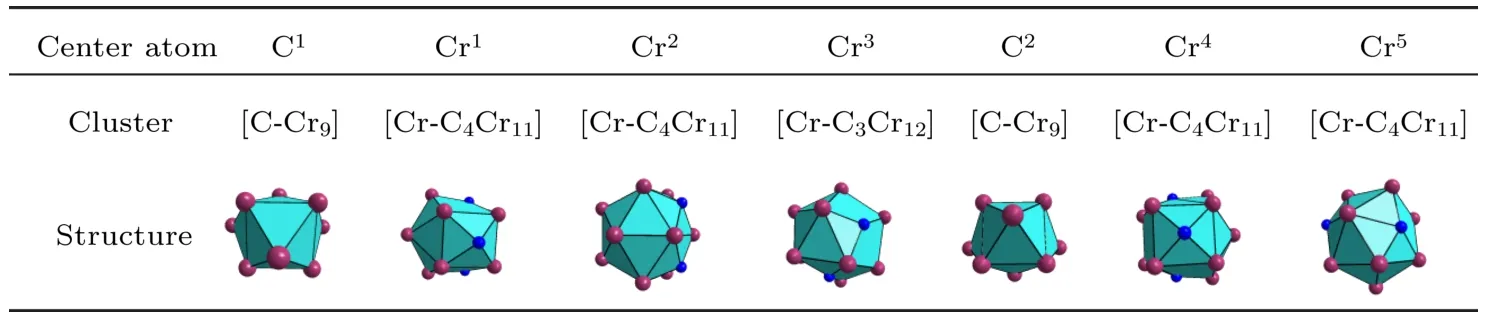
表3 (网刊彩色)Cr7C3相不同原子占位对应的团簇Table 3.(color online)Clusters centered by di ff erent non-equivalent sites in Cr7C3.

表4 (网刊彩色)Cr3C2相不同原子占位对应的团簇Table 4.(color online)Clusters centered by di ff erent non-equivalent sites in Cr3C2.

3.2定义主团簇

在晶体结构中,往往存在多个团簇,例如在表2中可以看到五种团簇.但是进入描述相关稳定熔体成分式的团簇只有一个,即为主团簇,是指某一合金相中最能反映其短程有序结构特征的第一近邻配位多面体,具有较高的原子密堆度,且团簇与团簇之间具有较高的孤立度［23].理想密堆情况下,团簇中心原子与近邻壳层原子之间以及近邻壳层原子与近邻壳层原子之间均为相切关系［24].而孤立度则反映了团簇之间的堆垛特征,团簇之间距离越远,其孤立度越大,团簇共享越少.

随着团簇加连接原子模型的发展,选取主团簇的方法趋于完善,目前倾向于以孤立度和球周期性为准则,从已定义出的团簇中选出最能反映短程有序结构特征的主团簇［15,17,19,25].非晶材料的电子结构及其稳定性取决于费米球和赝布里渊区的相互作用.若费米球与赝布里渊区相切,则此时费米能级处的电子态密度最低,系统稳定性最高［26,27].在满足上述电子结构稳定性的约束下,液体或者非晶态结构中,任意原子周围的原子密度径向分布呈振荡形式,符合Friedel振荡;在金属体系中,可用理想有效对势函数Φ(r)∝−sin(2kFr)/r3描述,该函数具有振荡形式,满足球周期性,即其极小值落在以某种特定波长λFr为周期的径向距离rn=(1/4+n)λFr上,而其极小值对应于原子密度的极大值,这样导致了原子壳层状的球周期分布.这里的λFr为Friedel振荡的波长,数值上等于2π/2kF(kF为费米球半径).我们的前期工作［16,17,28]指出,主团簇满足rn=(1/4+n)λFr,保证了团簇中原子分布的球周期性,理想主团簇的总原子密度径向分布函数与理想有效对势函数分别以波长2π/kP和2π/2kF的形式分布,且满足共振条件2kF=kP.其中,kP为赝布里渊区宽度.

此外,团簇的孤立度数值上用团簇共享后的有效原子个数与团簇的总原子个数的比值来表示,但由于原子并非具有确定半径的刚性球体,会导致该几何计算方法失准.团簇共振模型指出,在理想金属玻璃中,主团簇之间没有搭接,团簇间距满足r3=2.6r1.因此,可用团簇间距有效地表示团簇的孤立程度.在团簇的总原子密度径向分布函数中,团簇中心原子到与其具有相同占位的最近邻原子的距离越接近团簇间距r3,则该团簇的孤立度就越大［17].按照如下步骤,即可定义以合金相中不同原子占位为心的主团簇.

1)确定以合金相中不同原子占位为心的所有团簇.例如,Cr23C6相中有5个非等效的原子占位,分别为Cr1,Cr2,C,Cr3和Cr4;对应的5个团簇,依次为[Cr-Cr12C6],[Cr-Cr16],[C-Cr9],[Cr-C3Cr10]和[Cr-C2Cr12].

2)做出以不同原子占位为心的总原子密度径向分布图.团簇的总原子密度径向分布函数n(r)=N(r)/(4πr3/3),其中N(r)代表以任意给定原子为心所做半径为r的球所包围的原子个数,可通过累加r所包围的壳层原子数目获得,壳层原子排布情况如表5所列.图3给出了以Cr23C6相中不同原子占位为心的总原子密度径向分布.这里,纵坐标表示总原子密度,而横坐标r/λFr为任意位置到中心原子的距离与Friedel振荡波长的比值［17].

表5 Cr23C6相中不同原子占位对应的最近邻壳层距离、团簇、有效团簇、壳层原子排布、配位数及团簇的平均半径Table 5.For phase Cr23C6,the innermost shell distances,complete clusters,reduced clusters,atomic shells,coordination numbers and cluster radius r1centered by non-equivalent sites.

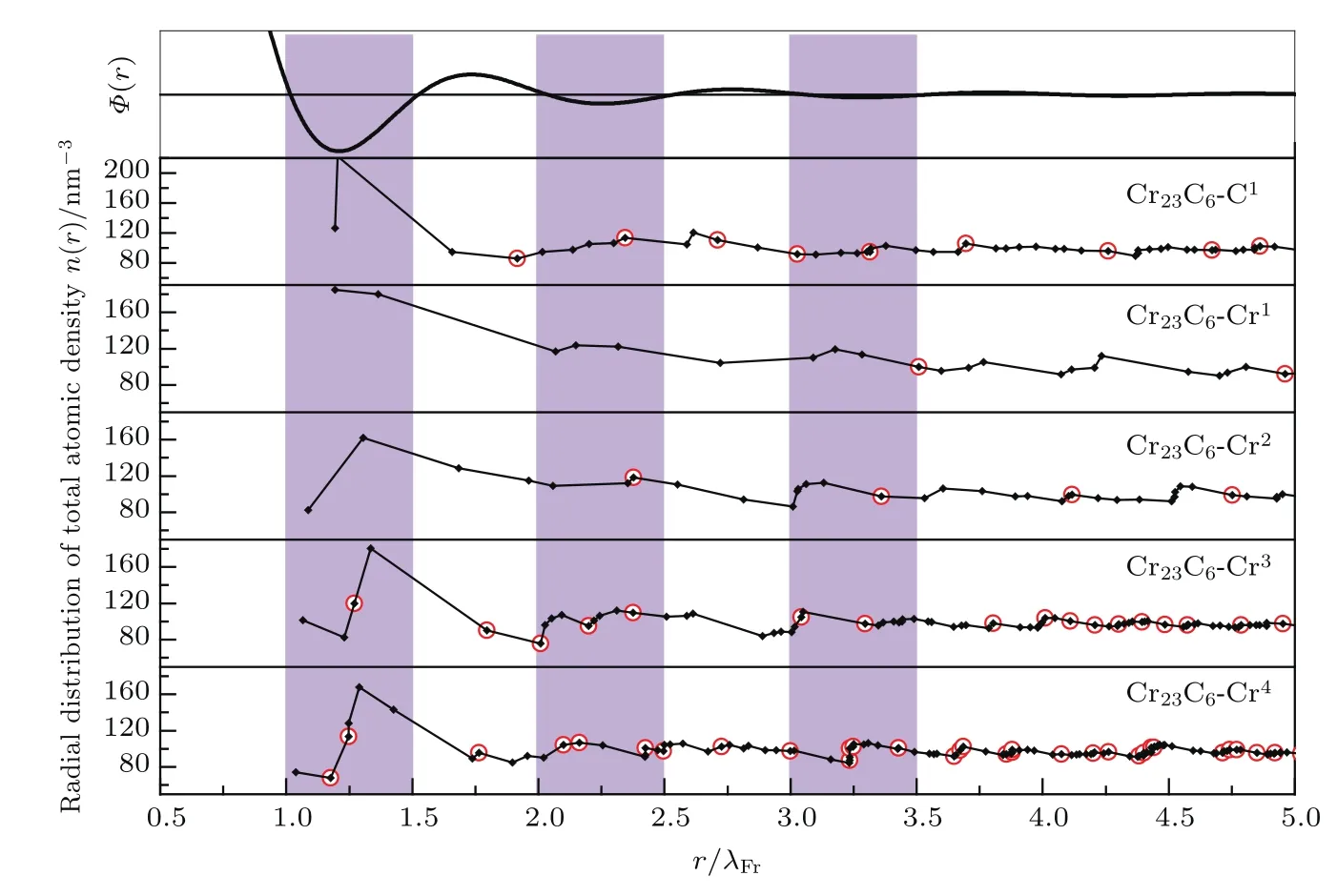
图3 (网刊彩色)理想有效对势函数分布和以Cr23C6相中5个不同原子占位为心的总原子密度径向分布,图中,势函数Φ(r)中波谷的分布区域由阴影覆盖,而与团簇中心原子具有相同的原子占位则由红色圆环圈出Fig.3.(color online)Idealized e ff ective pair potential distribution function and radial distribution of total atomic density centered by di ff erent non-equivalent sites in the phase Cr23C6.The distribution areas of the troughs in the potential function Φ(r)are covered by shadows and atomic sites in the red circles are the same as the center atom of the cluster.

3)对比以不同原子占位为心的总原子密度径向分布与理想有效对势函数分布,越接近共振状态,则以该原子占位为心定义的团簇,其球周期性越明显.图3中,自上而下依次为理想有效对势函数分布和以Cr23C6相中5个不同原子占位为心的总原子密度径向分布.经比较发现,Cr23C6相中以C1及Cr2原子作为中心原子的总原子密度径向分布与理想有效对势函数分布均较接近于共振状态,则团簇[C-Cr9]与[Cr-Cr16]有较为明显的球周期性分布特征.

4)比较团簇中心原子到和其具有相同占位的最近邻原子的距离与r3之间的关系,该距离越接近于团簇间距r3,则该团簇的孤立度就越大.如图3所示,Cr23C6相中,与团簇中心原子具有相同占位的最近邻原子C1和Cr2分别位于r/λFr为1.9163及2.3764处,后者与团簇间距r3相差略小;但考虑到团簇密堆性,得到R［C-Cr9]与R［Cr-Cr16]分别为0.71875和1.可见,R［C-Cr9]更接近于对应配位数下理想的R∗［18],则团簇[C-Cr9]的密堆度更高(中心溶质原子与壳层溶剂原子理想密堆时CN9与CN16对应的原子半径比R∗分别为0.710和1.183).比较发现,[C-Cr9]的团簇密堆率相较于[Cr-Cr16]大得多,因此选取[C-Cr9]为Cr23C6相的主团簇.同样地,将主团簇的定义方法引入到Cr-C二元体系中的其他合金相Cr7C3与Cr3C2,可以获得最能体现合金相Cr7C3与Cr3C2短程有序结构特征的主团簇,分别为[C-Cr9]和[C-Cr8].图4和图5分别给出了以Cr7C3与Cr3C2相中不同原子占位为心的总原子密度径向分布.

综上可得,Cr-C体系共晶点Cr86C14与Cr67.4C32.6两侧的合金相Cr,Cr23C6,Cr7C3,Cr3C2所对应的主团簇分别为[Cr-Cr14],[C-Cr9],[C-Cr9]及[C-Cr8].以共晶成分两侧合金相的主团簇搭配2,4或6个连接原子,构成双团簇成分式,即可解析其共晶成分.描述共晶成分Cr86C14和Cr67.4C32.6的双团簇成分式因此为Cr86C14≈[C-Cr9+Cr-Cr14]CrC3和Cr67.4C32.6≈[C-Cr9+CCr8]C6,其误差值分别为0.28 at.%与0.85 at.%,成分误差小于1 at.%.

图4 (网刊彩色)Cr7C3相中以不同原子占位为心的总原子密度径向分布Fig.4.(color online)Radial distribution of total atomic density centered by di ff erent non-equivalent sites in the phase Cr7C3.

图5 (网刊彩色)Cr3C2相中以不同原子占位为心的总原子密度径向分布Fig.5.(color online)Radial distribution of total atomic density centered by di ff erent non-equivalent sites in the phase Cr3C2.

4 结 论

本文将团簇加连接原子结构模型引入Cr-C体系中,得到了共晶相Cr,Cr23C6,Cr7C3和Cr3C2对应的团簇.以团簇的孤立度及原子排布的球周期性为准则,并兼顾团簇密堆率,确定出合适的主团簇,搭配2,4或6个连接原子构成双团簇共晶式,成功解析了Cr-C体系的共晶成分,得到了由双团簇式表示的共晶点成分式Cr86C14≈[C-Cr9+Cr-Cr14]CrC3和Cr67.4C32.6≈ [C-Cr9+C-Cr8]C6.本文详细给出了共晶成分解析的标准步骤,CrC体系的共晶成分解析结果进一步证实了团簇加连接原子模型在共晶点解析中的普适性,并可从理论上支持相关体系的材料设计.

[1]Jellad A,Labdi S,Benameur T 2009J.Alloy.Compd.483 464

[2]Jelinek M,Kocourek T,Zemek J,Mikšovský J,Kubinová Š,Remsa J,Kopeček J,Jurek K 2015Mater.Sci.Eng.C46 381

[3]Taherian R 2014J.Power Sources265 370

[4]Wang H,Turner J A 2010Fuel.Cells10 510

[5]Miracle D B 2006Acta Mater.54 4317

[6]Tian H,Zhang C,Zhao J,Dong C,Wen B,Wang Q 2012Physica B407 250

[7]Shi L L,Xu J,Ma E 2008Acta Mater.56 3613

[8]Mudry S,Shtablavyi I,Shcherba I 2008Arch.Mater.Sci.Eng.34 14

[9]Pasturel A,Jakse N 2011Phys.Rev.B84 134201

[10]Sterkhova I V,Kamaeva L V 2014J.Non-Cryst.Solids401 241

[11]Guo J,Liu L,Liu S,Zhou Y,Qi X,Ren X,Yang Q 2016Mater.Design106 355

[12]Miracle D B 2004Nat.Mater.3 697

[13]Sheng H W,Luo W K,Alamgir F M,Bai J M,Ma E 2006Nature439 419

[14]Dong C,Wang Q,Qiang J B,Wang Y M,Jiang N,Han G,Li Y H,Wu J,Xia J H 2007J.Phys.D:Appl.Phys.40 R273

[15]Ma Y P,Dong D D,Dong C,Luo L J,Wang Q,Qiang J B,Wang Y M 2015Sci.Rep.5 17880

[16]Luo L J,Chen H,Wang Y M,Qiang J B,Wang Q,Dong C,Häussler P 2014Philos.Mag.94 2520

[17]Dong D D,Zhang S,Wang Z J,Dong C,Häussler P 2016Mater.Design96 115

[18]Miracle D B,Sanders W S,Senkov O N 2003Philos.Mag.83 2409

[19]Dong D D,Zhang S,Wang Z R,Dong C 2015J.Appl.Crystallogr.48 2002

[20]Friedel J 1958Nuovo.Cimento.7 287

[21]Häussler P 1992Phys.Rep.222 65

[22]Pearson W B,Villars P P,Calvert L D 1985Pearson’s Handbook of Crystallographic Data for Intermetallic Phases(Materials Park,Ohio:ASM International)

[23]Du J,Wen B,Melnik R,Kawazoe Y 2014Acta Mater.75 113

[24]Wu Z W,Li M Z,Wang W H,Liu K X 2015Nat.Commun.6 6035

[25]Wang Z R,Qiang J B,Wang Y M,Wang Q,Dong D D,Dong C 2016Acta Mater.111 366

[26]Oberle R,Beck H 1979Solid State Commun.32 959

[27]Nagel S R,Tauc J 1975Phys.Rev.Lett.35 380

[28]Häussler P 1985J.Phys.Colloques46 C8-361

PACS:21.60.Gx,61.43.Bn,61.46.BcDOI:10.7498/aps.66.092101

Explanation of Cr-C eutectic points using the cluster-plus-glue-atom model∗

Wang Tong1)Hu Xiao-Gang1)2)Wu Ai-Min1)Lin Guo-Qiang1)Yu Xue-Wen2)Dong Chuang1)†

1)(Key Laboratory of Materials Modi fi cation by Laser,Ion and Electron Beams Ministry of Education,Dalian University of

Technology,Dalian 116024,China)2)(Dalian Nano-Crystal Tech Co.Ltd,Dalian 116600,China)

9 November 2016;revised manuscript

3 February 2017)

Cr-C system is an important protective coating material for its high hardness,good corrosion resistance and electrical conductivity.It is also a typical eutectic system,where all stable phases are involved in the eutectic reactions.According to our previous work,binary eutectic liquids satisfy the dual-cluster short-range-order structural model,i.e.,a eutectic liquid is composed of two stable liquid subunits respectively issued from the two eutectic phases and each one formulates the same ideal metallic glass[cluster](glue atom)1or3,where the nearest-neighbor cluster is derived from a devitri fi cation phase.Therefore a eutectic liquid can always be formulated as two nearest-neighbor clusters plus two,four,or six glue atoms.The key step towards understanding a eutectic composition is then to obtain the right clusters from the two eutectic phases for use in the formulation of the glassy/eutectic composition,which we call the principal clusters.In this paper,Friedel oscillation and atomic dense packing theories are adopted to identify the principal clusters of Cr-C eutectic phases for the objective of establishing the dual cluster formulas for the eutectic compositions.First,clusters in eutectic phases Cr,Cr23C6,Cr7C3and Cr3C2are de fi ned by assuming that all the nearest neighbors are located within the fi rst negative potential minimum zone in Friedel oscillation,which causes a cuto ffdistance to be less than 1.5 times the innermost shell distance.Second,by comparing all the radial distribution pro fi les of total atomic density centered by each cluster in a given phase structure,the one exhibiting the most distinct spherical periodicity feature is selected as the principal cluster.Moreover,the principal clusters are the most separated from each other among all the clusters in the same phase,showing the highest degree of cluster isolation.Under the criteria of the cluster distribution following spherical periodicity order and of the cluster isolation,the following principal clusters are derived:rhombidodecahedron CN14[Cr-Cr14]from Cr,capped trigonal prism CN9[C-Cr9]from Cr23C6and Cr7C3,and[C-Cr8]from Cr3C2.Via these examples,the principal cluster identi fi cation procedures are detailed.Third,the thus selected principal clusters are matched with appropriate glue atoms to construct the dual cluster formulas for the Cr-C eutectics Cr86C14and Cr67.4C32.6,i.e.,[Cr-Cr14+C-Cr9]CrC3≈Cr86.2C13.8and[C-Cr9+C-Cr8]C6≈Cr68.0C32.0,respectively.This work proves the universality of the cluster-plus-glue-atom model in explaining the composition of binary eutectics and lays a theoretical foundation for the composition design of Cr-C based materials.

Cr-C,cluster-plus-glue-atom model,eutectics,principal cluster

10.7498/aps.66.092101

∗国家重点研发计划(批准号:2016YFB0101206)资助的课题.

†通信作者.E-mail:dong@dlut.edu.cn

*Project supported by the National Key Research and Development Program of China(Grant No.2016YFB0101206).

†Corresponding author.E-mail:dong@dlut.edu.cn