灰气体加权和辐射模型综合评估及分析∗
楚化强冯艳 曹文健 任飞 顾明言2)‡
1)(安徽工业大学能源与环境学院,马鞍山 243002)2)(安徽工业大学,冶金减排与资源综合利用教育部重点实验室,马鞍山 243002)
灰气体加权和辐射模型综合评估及分析∗
楚化强1)2)†冯艳1)曹文健1)任飞1)顾明言1)2)‡
1)(安徽工业大学能源与环境学院,马鞍山 243002)2)(安徽工业大学,冶金减排与资源综合利用教育部重点实验室,马鞍山 243002)
(2016年12月26日收到;2017年2月24日收到修改稿)
在O2/CO2气氛下,参与性介质的非灰气体辐射特性表现出不同于空气气氛下的特性,因此,非灰气体辐射模型的选择和应用在换热过程中将变得十分重要.基于统计窄谱带模型,本文综合评估近年发展应用较广的灰气体加权和(WSGG)模型.结果表明,几种WSGG模型的预测值总体趋势正确,但仍存在着一定的差别.对于发射率,Dorigon等(2013Int.J.Heat Mass Transfer64 863)和Bordbar等(2014Combust.Flame161 2435)的WSGG模型与基准模型符合较好,相对误差小于20%.与离散坐标法结合,本文求解了PH2O/PCO2=1,2时的一维平行平板间辐射换热问题.结果显示,由Dorigon等和Bordbar等的WSGG模型得到的辐射热源和热流密度分布的相对误差均较小(10%左右).Johansson等(2011Combust.Flame158 893)和Bordbar等的WSGG模型具有更广的适用范围.
气体辐射,灰气体加权和模型,发射率,离散坐标法
1 引 言
富氧燃烧是一种新型、高效、低污染燃烧技术.辐射换热是高温炉膛、工业炉等大型高温系统的主要传热方式,而辐射换热的准确度在很大程度上取决于燃烧产物辐射特性的精确估算.特别是在富氧气氛下,随着CO2这种辐射性气体成分的增加,辐射换热在整个过程中所占的比重将大大增加.非灰气体辐射特性表现出不同于空气气氛下的特性,因此,非灰气体辐射模型的选择在换热计算过程中将变得十分重要.灰体假设是一种最简单的气体模型,虽然计算简单易行,但存在着较大的误差[1].随着对精度的要求越来越高,灰体假设已经不能满足工业和研究的要求,因此必须考虑燃烧产物的非灰辐射特性.由于辐射传递方程的多维性和对光谱吸收系数的严重依赖性,如何有效而又准确地计算辐射换热问题是当前各国学者面对的一大挑战.
对于非灰辐射特性的研究,最初主要在大气辐射领域应用,随后被应用到热物理领域[1],并且这些光谱特性也被应用于光谱检测[2−5].经过大量学者的努力,目前已经发展了各种光谱模型,根据其特点可分为两类[1]:一类是以气体透射率、有效带宽等作为辐射特性的谱带模型,如窄谱带模型、宽谱带模型,这类模型仅仅适用于积分形式的辐射传递方程;另一类是以气体的吸收系数作为基本辐射特性的光谱模型,如逐线(line-by-line,LBL)法、灰气体加权和(weighted sum of gray gases,WSGG)模型、基于光谱线的灰气体加权和(spectral-linebased weighted-sum-of-gray-gases,SLW)模型、统计窄谱带关联K模型、全光谱关联K模型等,此类模型适用于任意形式的辐射传递方程.
LBL法是研究气体非灰辐射特性最精确的模型,也是发展其他近似非灰辐射模型的根本,常作为基准解来检验近似模型的准确性[6,7],但计算非常耗时,特别是多维问题.WSGG模型是一种兼具效率和精度的理想近似模型,特别是随着高精度光谱数据库的发展,使得该模型具有更广的应用前景.
1967年,Hottle和Saro fi m[8]利用区域法研究非灰参与性介质辐射传热问题时首次提出WSGG模型.1982年,Smith等[9]拟合得到了至今应用最广泛的WSGG模型参数.1991年,结合球形谐波法,Modest[10]将WSGG模型进行了进一步推广,并表明WSGG模型可与求解辐射传递方程的任意数值求解方法相结合.随后,WSGG模型得到了广泛的应用和发展.Sou fi ani和Djavdan[11]利用统计窄谱带(SNB)模型得到的发射率拟合PH2O/PCO2=2(PH2O表示水分压,PCO2表示二氧化碳分压)时WSGG模型参数,并将其应用于甲烷空气燃烧产物模拟.基于光谱数据库,Webb课题组[12,13]发展了WSGG模型,并提出了SLW模型,大大提高了WSGG模型的计算精度.Baek课题组[14,15]采用Hottel和Smith[7]的参数将WSGG模型应用于液体喷雾燃烧模拟,并进一步考虑了颗粒物非灰辐射特性.利用光谱数据库,Taine研究组[16,17]提出了与SLW模型类似的吸收分布函数模型.Yang和Song[18]基于窄谱带模型拟合了多组参数,但应用不广.对气体火焰炉中气体的辐射特性,Liu等[19]比较了基于两种参数数据库的WSGG模型和简单灰气体模型的三维辐射换热计算结果.从重排角度出发,Modest课题组[1]改进WSGG模型,并提出了一种新的全光谱K分布模型,大大提高了辐射换热计算效率.Johansson等[20]采用SNB模型拟合了WSGG模型参数数据库,与前人的工作不同,他们还首次拟合了气体吸收系数随水蒸气与二氧化碳分压比的多项式.Yin等[21]利用宽谱带模型拟合了适用于富氧气氛的多个工况下WSGG模型参数数据库.基于HITEMP2010光谱数据库,França课题组[22,23]拟合得到了WSGG模型参数数据库,并给出了吸收系数的关联式,另外他们还得到了烟黑的参数.Bordbar等[24]利用LBL法和HITEMP2010数据库得到了WSGG模型参数数据库和吸收系数关联式.基于LBL法,Bahador和Sunden[25]拟合得到了多个大气压力下WSGG模型参数.图1给出了近五十年关于WSGG模型发展的重要代表性文献.

图1 (网刊彩色)WSGG模型发展重要代表作Fig.1.(color online)Important representatives for WSGG model development.
综上所述,目前基于HITEMP2010数据库得到WSGG模型参数是比较准确的,但仅有少数学者给出了吸收系数随气体分压比变化的关联式.对于每个参数数据库,他们的结果都与各自的基准解符合较好,但缺乏统一的比较和评估.基于此,本文将系统评估最近发展和应用较广的七组WSGG参数,为实际应用的选择提供理论依据.此外,本文还采用了基于最新数据库的SNB模型,并将此结果作为基准解.
2 计算模型
对于具有吸收、发射特性的介质,其光谱辐射传递方程为[1]

它描述了辐射强度沿着路径方向ˆs上的变化.
对于漫反射边界,其边界条件为
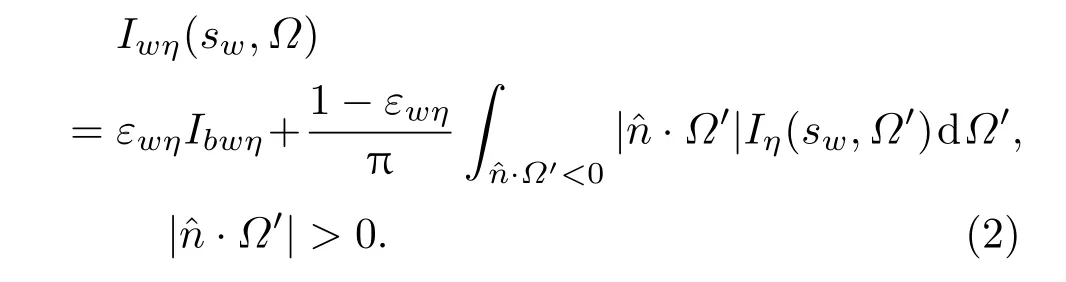
2.1 SNB模型
SNB模型中,窄带内的平均气体透射率τη为

2.2 WSGG模型
WSGG模型主要思想是用几种灰气体加一种透明气体来模拟实际气体的非灰辐射特性,如图2所示.经典WSGG模型均是基于其他模型(如LBL法、窄谱带模型、宽谱带模型等)通过拟合固定工况下的发射率得到一系列参数,拟合的准确度与基准模型的精度有关.对于吸收系数,早期WSGG模型拟合得到几个固定值.为了提高精度和拓宽通用工况,近年来,学者开始拟合得到吸收系数随气体分压比变化的关联式.
气体总发射率可由I种灰气体加权得到,即

式中,P是气体总压,ai是第i种气体吸收系数为Ki时的权重,可拟合成关于温度T的J阶多项式,即

需要指出的是,对于(5)式中的b,早期WSGG模型均拟合为常数.最近,Jonhansson等[20]将b拟合成更为准确的关于分压比的多项式,并且(5)式中的T取为(T/1200 K);Bordbar等[24]也拟合出类似的关联式.b的关联式如下:

为了考虑实际气体中“透明窗口”效应,WSGG模型引入一种透明气体,即K0=0,其权重采用下式得到

对于吸收系数Ki,自Johansson等[20]首次提出吸收系数关联式后,有若干个关联式被提出.Bordbar等[24]也拟合出类似的关联式.Johansson等[20]的表达式为

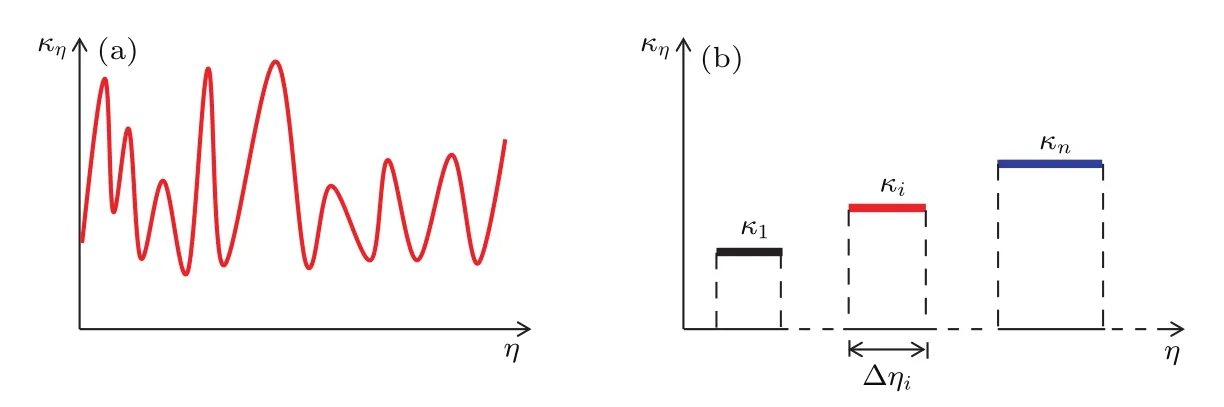
图2 (a)实际气体吸收系数分布;(b)WSGG模型思想Fig.2.(a)High-resolution absorption coefficient distribution of real gas;(b)the representation of the WSGG model.

表1WSGG模型参数汇总Table 1.Summary of WSGG model parameters.
在得到吸收系数和权重之后,就可采用一定的数值求解方法来求解辐射传递方程.首先对每种灰气体单独进行辐射传递方程求解,然后将各种灰气体热流加权求和得到总热流.由于根据WSGG模型可直接得到气体的吸收系数,因此WSGG模型很容易和任意形式的辐射传递方程求解方法结合,并且计算效率较高,本文采用离散坐标法求解辐射传递方程.表1列出了本文所评估的七组典型WSGG模型参数.
3 结果与讨论

图3 (网刊彩色)水蒸气与二氧化碳混合物总发射率随温度变化情况及其相对误差 (a)总发射率,PH2O/PCO2=1;(b)总发射率,PH2O/PCO2=2;(c)相对误差,PH2O/PCO2=1;(d)相对误差,PH2O/PCO2=2Fig.3.(color online)The variation of the total emittance with the temperature using the several models:(a)The total emittance for PH2O/PCO2=1;(b)the total emittance for PH2O/PCO2=2;(c)the relative errors for PH2O/PCO2=1;(d)the relative errors for PH2O/PCO2=2.
文献[6,7]表明,采用SNB模型所得结果与基于LBL法所得预测值符合较好,并且SNB模型计算效率更高,因此本文采用SNB模型作为基准模型,所评估的WSGG模型参数由表1中的文献给出.
图3给出了PH2O/PCO2=1,2时不同路径下的发射率随温度变化的分布.图中考虑三个路径即0.01,0.1和1 m三种情况.由图3可见,在路径长度比较小的情况下,Yin等[21]和Smith等[9]的WSGG模型与基准模型差别较大,其他WSGG模型与基准模型结果符合较好,以误差最大的路径(0.01 m)为例,其相对误差均在20%—(−20%).随着路径的增大,总体发射率之间差别变小.对于不同压力比,模型间预测误差变化不大.总体而言,所有WSGG模型预测结果比较准确.需要指出的是,由于Yin等[21]和Smith等[9]的WSGG模型误差相对较大,后面的比较中,本文未做更进一步比较,仅采用Smith等[9]的WSGG 模型作为比较.
图4给出了不同温度下发射率随压力行程(压力乘以路径)的变化.图中采用了七种WSGG模型参数计算了水蒸气和二氧化碳的分压比为2、压力行程范围为0—60 atm.m和温度分别为1000,1500,1800和2400 K时混合气体总发射率,并与SNB模型的计算结果进行了比较.从图4可以看出,随着温度的升高混合气体的总发射率降低.比较各个模型发现,Kangwanpongpan等[22]的WSGG模型结果偏高.Smith等[9]的WSGG模型得到的总发射率在压力行程范围为0—15 atm.m时变化趋势和其他六种模型一致,但是当压力行程范围大于15 atm.m时,混合气体的总发射率趋于定值,且与基准解差别越来越大.随着温度的升高,Bordarbar等[24]和Dorigon等[23]的WSGG模型与SNB结果符合得越来越好.在高温情况下,Bordarbar等[24]的WSGG模型结果与SNB结果符合得非常好.
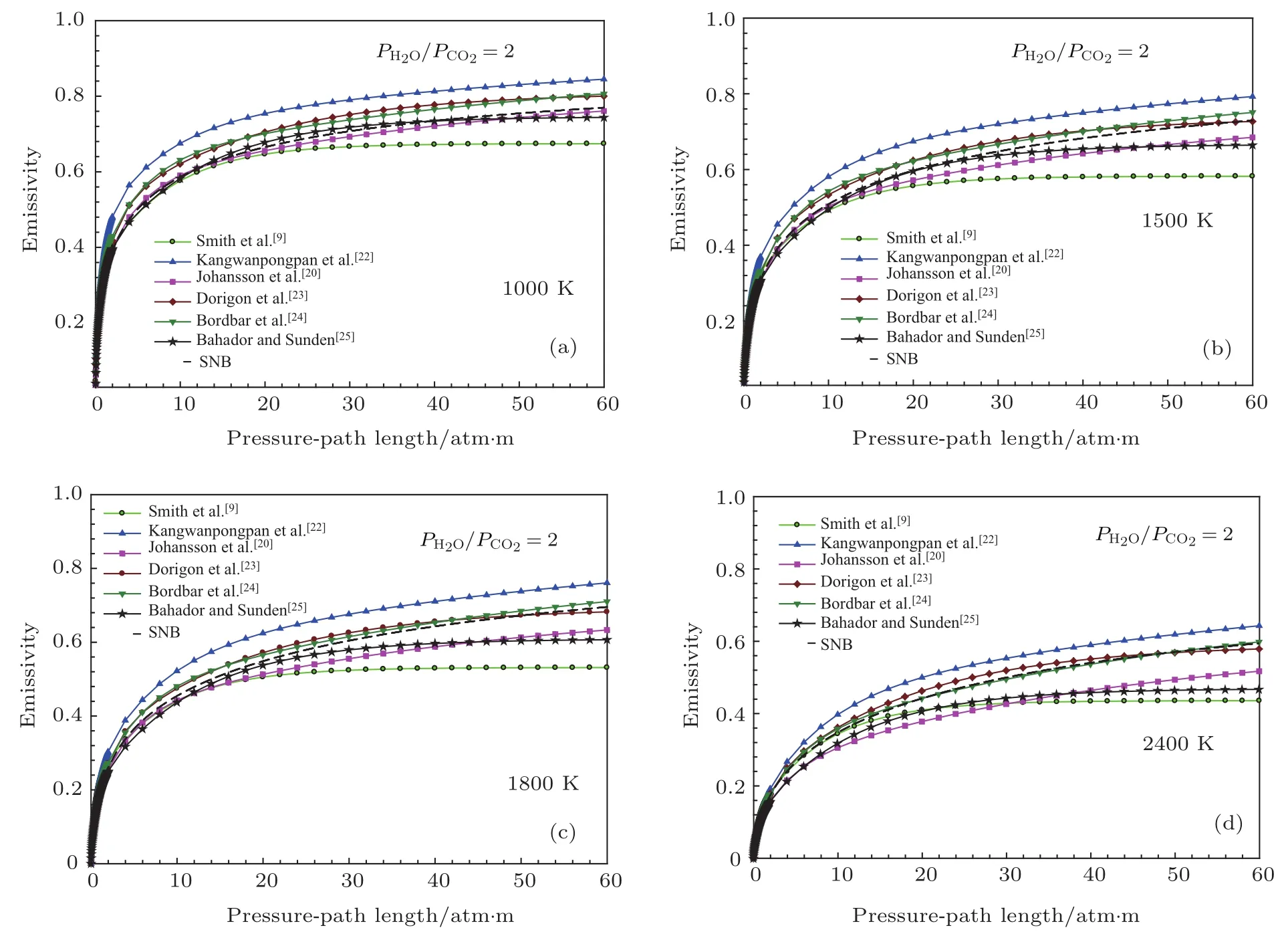
图4 (网刊彩色)不同温度下发射率随压力行程的变化Fig.4.(color online)The variation of the total emittance with the pressure-path length obtained by the WSGG models and SNB model with di ff erent temperature.
为进一步评估各个WSGG模型参数,本文以一维平行平板间N2/CO2/H2O混合物辐射换热为例,将这些辐射模型和离散坐标法结合求解辐射传递方程. 考虑四种工况:(算例I)PH2O=PCO2=0.1,即PH2O/PCO2=1,平行平板间距L=1 m;(算例II)PH2O=PCO2=0.1,即PH2O/PCO2=1,平行平板间距L=10 m;(算例III,与算例I温度分布不同)PH2O=PCO2=0.1,即PH2O/PCO2=1,平行平板间距L=1 m;(算例IV)PH2O=2PCO2=0.2,即PH2O/PCO2=2,平行平板间距L=1 m.前两个算例的温度分布为T(x)=1250−750cos(2πx/L),后两个算例的温度分布为T(x)=400+1400sin2(2πx/L),其分布如图5所示.由图5可知,第一种温度分布只有一个峰值,而第二种温度分布有两个峰值、一个谷值.由于温度分布呈非等温分布,这更能评估各个模型的准确度.
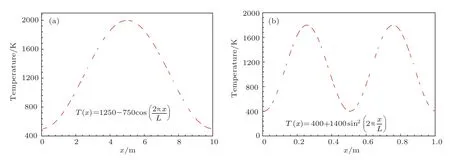
图5 四种工况的温度分布Fig.5.The temperature distributions of four cases.

图6 (网刊彩色)各个模型得到的辐射热源、辐射热流密度及其相对误差(算例I) (a)辐射热源;(b)辐射热流密度;(c)辐射热源的相对误差;(d)辐射热流密度的相对误差Fig.6.(color online)Comparison between di ff erent mdoels(case I):(a)Radiative heat source;(b)radiative heat fl ux;(c)relative errors for radiative heat source;(d)relative errors for radiative heat fl ux.
基于第一种温度分布,图6和图7给出了PH2O/PCO2=1时辐射热源、辐射热流密度及其相对误差的比较.由于温度分布呈对称分布,且在中心处达到最高值,因此辐射热源在中心处由于更多的辐射能被辐射出去而处于其分布的谷底,辐射热流密度在中心处为零.由图6(a)、图6(b)、图7(a)和图7(b)的整体趋势上看,基于各个WSGG模型的结果均与SNB模型的结果符合较好,仅在拐点处有差别.由图6(c)、图6(d)、图7(c)和图7(d)可知,与SNB模型的结果相比,所有WSGG模型的相对误差均在±30%之间,特别是辐射热流密度,其相对误差在5%—(−15%)之间.对比各个模型可发现,基于Dorigon等[23]和Kangwanpongpan等[22]的WSGG模型参数,其结果与SNB模型的结果符合较好,特别是中心区域.此外,Bordbar等[24]、Johansson等[20]及Bahador和Sunden[25]的WSGG模型结果也尚可接受.需要指出的是,随着路径的增加,辐射热源和辐射热流的相对误差减小.

图7 (网刊彩色)各个模型得到的辐射热源、辐射热流密度及其相对误差(算例II) (a)辐射热源;(b)辐射热流密度;(c)辐射热源的相对误差;(d)辐射热流密度的相对误差Fig.7.(color online)Comparison between di ff erent mdoels(case II):(a)Radiative heat source;(b)radiative heat fl ux;(c)relative errors for radiative heat source;(d)relative errors for radiative heat fl ux.
图8和图9给出了水蒸气和二氧化碳的分压比为1,2时的辐射热源、辐射热流密度及其相对误差的比较,温度分布由图5(b)给出.从图8(a)可以看出,在中心线的两边热源的分布是对称的,绝对值最大的点分别出现在x=0.25和0.75 m附近,从温度分布图5(b)可以看出这两点的温度最高.需要注意的是,图9还给出了文献[29]中的LBL法结果,可以看出,SNB结果与文献数据符合得非常好.尽管在绝对值最大处其他的几种模型的结果都与基准解有偏差,但相对误差均在±30%之间.总体上可发现,Dorigon等[23]、Bordbar等[24]及Bahador和Sunden[25]的WSGG模型结果与SNB模型结果符合较好,此外,Kangwanpongpan等[22]及Johansson等[20]的WSGG模型结果也比较理想.需要指出的是,随着水蒸气和二氧化碳分压比的增加,辐射热源和辐射热流的相对误差增大.

图8 (网刊彩色)各个模型得到的辐射热源、辐射热流密度及其相对误差(算例III) (a)辐射热源;(b)辐射热流密度;(c)辐射热源的相对误差;(d)辐射热流密度的相对误差Fig.8.(color online)Comparison between di ff erent mdoels(case III):(a)Radiative heat source;(b)radiative heat fl ux;(c)relative errors for radiative heat source;(d)relative errors for radiative heat fl ux.
值得注意的是,Johansson等[20]和Bordbar等[24]的WSGG模型参数给出了系数的表达式,因此他们的参数适用范围更广.此外,分析这些模型的差别发现,其主要原因在于各个模型拟合参数时的基准不同.
4 结 论
通过分析比较,本文主要得到以下4点结论.
1) 在小路径下,Yin等[21]和Smith等[9]的WSGG模型得到的总发射率与基准模型的结果差别较大,而其他模型则与基准模型符合得较好;路径越大,各个WSGG模型解与基准解符合越好.
2)混合气体的发射率随光程路径的增大而增大.Smith等[9]和Kangwanpongpan 等[22]的WSGG模型与SNB模型的计算结果存在较大的偏离.随着温度的升高,Bordarbar等[24]和Dorigon等[23]的WSGG模型结果与SNB结果符合得越来越好.在高温情况下,Bordarbar等[24]的WSGG模型结果与SNB结果符合得非常好.
3)与基准解相比,六种WSGG模型与离散坐标法耦合求解的辐射热源、辐射热流密度虽有偏差,但是总体上符合较好,相对误差均在±30%之间. 基于Dorigon等[23]和Bordbar等[24]的WSGG模型参数,其结果与SNB模型的结果符合较好. 此外,基于Johansson等[20]、Kangwanpongpan等[22]及Bahador和Sunden[25]的WSGG结果也尚可接受.
4)综合比较,在实际应用中可选择Dorigon等[23]、Bordbar等[24]的WSGG模型来计算辐射换 热 问 题. Johansson 等[20]和 Bordbar等[24]的WSGG模型具有更广的适用范围,但与基准模型之间的误差相比要大.

图9 (网刊彩色)各个模型得到的辐射热源、辐射热流密度及其相对误差(算例IV) (a)辐射热源;(b)辐射热流密度;(c)辐射热源的相对误差;(d)辐射热流密度的相对误差Fig.9.(color online)Comparison between di ff erent mdoels(case IV):(a)Radiative heat source;(b)radiative heat fl ux;(c)relative errors for radiative heat source;(d)relative errors for radiative heat fl ux.
[1]Modest M F 2013Radiative Heat Transfer(3rd Ed.)(San Diego:Academic Press)p303
[2]Peng Z M,Ding Y J,Zhai X D 2011Acta Phys.Sin.60 104702(in Chinese)[彭志敏,丁艳军,翟晓东2011物理学报60 104702]
[3]Lan L Q,Ding Y J,Jia J W,Du Y J,Peng Z M 2014Acta Phys.Sin.63 083301(in Chinese)[蓝丽娟,丁艳军,贾军伟,杜艳君,彭志敏2014物理学报63 083301]
[4]Zhang Z R,Wu B,Xia H,Pang T,Wang G X,Sun P S,Dong F Z,Wang Y 2013Acta Phys.Sin.62 234204(in Chinese)[张志荣,吴边,夏滑,庞涛,王高旋,孙鹏帅,董凤忠,王煜2013物理学报62 234204]
[5]Wang M R,Cai T D 2015Acta Phys.Sin.64 213301(in Chinese)[王敏锐,蔡廷栋 2015物理学报 64 213301]
[6]Chu H Q,Liu F S,Zhou H C 2011Int.J.Heat Mass Transfer54 4736
[7]Chu H Q,Liu F S,Zhou H C 2012Int.J.Therm.Sci.59 66
[8]Hottel H C,Saro fi m A F 1967Radiative Transfer(New York:McGraw-Hill)p20
[9]Smith T F,Shen Z F,Friedman J N 1982J.Heat Transfer104 602
[10]Modest M F 1991J.Heat Transfer113 650
[11]Sou fi ani A,Djavdan E 1994Combust.Flame97 240
[12]Denison M K,Webb B W 1993J.Heat Transfer115 1004
[13]Denison M K,Webb B W 1995J.Heat Transfer117 359
[14]Choi C E,Baek S W 1996Combust.Sci.Technol.115 297
[15]Yu M J,Baek S W,Park J H 2000Int.J.Heat Mass Transfer43 1699
[16]Riviere P,Sou fi ani A,Taine J 1995J.Quant.Spectrosc.Radiat.Transfer53 335
[17]Pierrot L,Riviere P,Sou fi ani A,Taine J 1999J.Quant.Spectrosc.Radiat.Transfer62 609
[18]Yang S S,Song T H 1999Int.J.Therm.Sci.38 228
[19]Liu F,Becker H A,Bindar Y 1998Int.J.Heat Mass Transfer41 3357
[20]Johansson R,Leckner B,Andersson K,Johnsson F 2011Combust.Flame158 893
[21]Yin C,Johansen L C R,Rosendahl L A,Kær S K 2010Energy Fuels24 6275
[22]Kangwanpongpan T,França F H R,da Silva R C,Schneider P S,Krautz H J 2012Int.J.Heat Mass Transfer55 7419
[23]Dorigon L J,Duciak G,Brittes R,Cassol F,Galarca M,França F H R 2013Int.J.Heat Mass Transfer64 863
[24]Bordbar M H,Wecel G,Hyppänen T 2014Combust.Flame161 2435
[25]Bahador M,Sunden B 2008ASME Turbo Expo 2008:Power for Land,Sea,and AirBerlin,Germany,June 9–13,2008 p1791
[26]Sou fi ani A,Taine J 1997Int.J.Heat Mass Transfer40 987
[27]Rivière P,Sou fi ani A 2012Int.J.Heat Mass Transfer55 3349
[28]Liu F,Gulder O L,Smallwood G J 1998Int.J.Heat Mass Transfer41 2227
[29]Cassol F,Brittes R,França F H R,Ezekoye O A 2014Int.J.Heat Mass Transfer79 796
PACS:42.68.Ca,96.25.Tg,47.70.Mc,47.70.–nDOI:10.7498/aps.66.094207
Comprehensive evaluation and analysis of the weighted-sum-of-gray-gases radiation model∗
Chu Hua-Qiang1)2)†Feng Yan1)Cao Wen-Jian1)Ren Fei1)Gu Ming-Yan1)2)‡
1)(School of Energy and Environment,Anhui University of Technology,Ma’anshan 243002,China)2)(Key Laboratory of Metallurgical Emission Reduction and Resources Recycling of Ministry of Education,Anhui University of Technology,Ma’anshan 243002,China)
26 December 2016;revised manuscript
24 February 2017)
In oxy-fuel combustion with CO2recycle,the non-gray gas radiative heat transfer characteristics of gaseous participating media are di ff erent from those in air-fuel combustion.Therefore,the choice of a non-gray gas radiation model should be carefully made since it plays an important role in modeling the oxy-fuel combustion system.Using the statistical narrow-band model as a benchmark,in this paper we provide a comprehensive assessment of the development of the weighted-sum-of-gray-gase(WSGG)model,which has been achieved in recent years.The results show that the predicted values obtained by the WSGG model are generally reasonably accurate,though some signi fi cant di ff erences still exist.For the total emissivity,the WSGG models by Dorigon et al.(2013Int.J.Heat Mass Transfer64 863)and Bordbar et al.(2014Combust.Flame161 2435)are consistent well with the benchmark model,within a relative error of less than about 20%.Under the conditions of PH2O/PCO2=1 and 2,the magnitudes of radiative heat transfer between two planar plates are calculated using the discrete-ordinate method and WSGG model.It is found that the radiative source and radiative net heat fl ux obtained using the WSGG model parameters of Dorigon et al.and Bordbar et al.are more accurate than using other parameters developed in the literature(about 10%relative errors).It is worth noting that the WSGG model parameters of Jonhansson et al.(2011Combust.Flame158 893)and Bordbar et al.have a wider range of applications.
non-gray gas radiation,weighted-sum-of-gray-gases model,total emissivity,discrete-ordinate method
10.7498/aps.66.094207
∗国家自然科学基金(批准号:51676002,51376008,51306001)和安徽省自然科学基金(批准号:1408085QE100)资助的课题.
†通信作者.E-mail:hqchust@163.com
‡通信作者.E-mail:mingyan_gu@qq.com
*Project supported by the National Natural Science Foundation of China(Grant Nos.51676002,51376008,51306001)and the Anhui Provincial Natural Science Foundation,China(Grant No.1408085QE100).
†Corresponding author.E-mail:hqchust@163.com
‡Corresponding author.E-mail:mingyan_gu@qq.com

