变化噪声下GNSS卫星信号的捕获算法的研究

曹 军，姚 楠，姜胜明

(1. 上海海事大学 信息工程学院，上海 201306； 2. 上海海事大学，上海 201306)



变化噪声下GNSS卫星信号的捕获算法的研究

曹 军1，姚 楠2，姜胜明2

(1. 上海海事大学 信息工程学院，上海 201306； 2. 上海海事大学，上海 201306)

当今社会，越来越多的不确定性噪声在城市中出现，这些噪声会被掺杂到有效的卫星信号中，造成信号的捕获失败。许多算法中设定的噪声比较固定，没有考虑到每个地方噪声变化的情况。文中基于快速傅里叶变换的并行捕获技术，结合前差分技术和相干积分，尝试消除这种不确定影响。其次，在此基础上进行各种噪声下的仿真，寻求捕获的判决门限的合理值。通过仿真表明，该算法可以有效地捕获卫星信号，并减少了计算的复杂度。

不确定噪声；前差分；判决门限；信号捕获

0 引言

全球卫星导航系统(GNSS)目前被广泛应用在生活中，GNSS具备定位、高精度导航的特点。同时，定位又是基于卫星信号的捕获，因此，许多学者在卫星信号的处理领域做了大量的工作[1-2]。在开阔的环境中，信号的强度为-153 dB，卫星接收机在非常短的时间内就可以捕获到有效的信号。但是，当信号在复杂的环境中，信号衰减，同时，各种不确定的噪声混入到信号中，这时，造成了低信噪比。对于卫星信号的捕获，可能不能捕获到有效的卫星，甚至会出现错误的捕获。

卫星信号的经典处理方法，主要有相干累积、非相干累积两种。相干累积可以用来提高信噪比，但是会受到导航电文反转和积分时间的影响。非相干积分不受频率误差的影响，但是却引进了平方误差，而且随着时间的延迟，这种平方损失越大[3]。针对信号的损失，对于信噪比增益的提高的分析也是不可或缺的部分。结合捕获的最基本的三种方式，提高增益也是一种比较基础的做法[4]。关于信号的处理，有研究人员提出前相关差分的捕获方案，在码片级的延迟上进行差分，因为是码片级的延迟，多普勒频差和导航数据几乎可以忽略不计，影响较小。但是这种方案的限制在于对于噪声的抑制不高。在此基础上，有人采取了新的做法，即前置滤波器，外加多重前相关差分检测的方式，有效地抑制了噪声，并且保留了对于多普勒频率敏感度低的优点[5]。为了处理信号的捕获，有学者最新提出使用平均相关技术，结合差分相干累积的方式，对GPS信号的C/A码并行捕获，虽然平均相关技术兼顾了处理增益和计算的复杂度，但是受限于使用的序列个数[6]。同时，在考虑到这些外在因素外，室内信号环境复杂，不仅信号在削弱，而且出现远近效应[7]，这个因素也需要被考虑进去。在中国的卫星系统领域，北斗已经走进人们日常生活，对于北斗信号形式的研究也越来越多[8]。在GPS与北斗系统同时存在的情况下，兼容性的研究同样重要，推进双模卫星信号基带处理算法的研究也是当前的重点[9]。

通过以上分析，本文基于FFT的并行捕获技术，结合前差分技术和相干积分，做了深入研究。同时使用了相干积分的最大值与第二大值的比值的方式，来提高捕获的准确性。

1 信号与噪声模型

信号包括L1、L2两个载波频率，对于民用来说，只需要L1上的信号，所以在L1频率分量上，某颗卫星的信号S(t)可以表示为：

S(t)=ApP(t)D(t)cos(2πf1t+Φ)+AcC(t)D(t)

sin(2πf1t+Φ)

(1)

L1上的P码与接收机产生的C/A码做相关运算后会被消逝成无用的噪声。为了简化运算，本文只关注每一颗卫星的L1频率上的C/A码信号，这时简化信号公式为：

S(t)=AcC(t-τ)D(t-τ)sin(2π(f1+fd)t+φ)

(2)

其中，Ac是信号的幅值，C(·)是C/A码信号，D(·)是导航电文的信息，f1为载波频率，fd为接收机与卫星之间由于相对运动而产生的多普勒频率，φ为信号初始相位，τ为码相位偏移。

假设噪声信号是两个高斯白噪声的线性组合，为N(k)：

N(k)=Y(k)+aY(k-1)

(3)

其中，Y(k)是均值为0、方差为σ2/2的高斯白噪声，a是权值。所以，噪声的概率密度是：

2 算法描述

卫星接收机的天线接收的卫星信号，其中夹杂着各种噪声，信号经过下变频处理，变成中频信号SLF。信号通过码片级的延迟，再与原始信号差分，这样可以保证位码序列的相关性，同时可以消除噪声的影响。然后通过相干累积的方式，提高信噪比，最后通过比值法判断是否是有效的卫星信号。

图1是本文研究内容的捕获流程框架。图中S(t+mΔt)表示信号的m个码片延迟，FFT表示快速傅里叶变换。

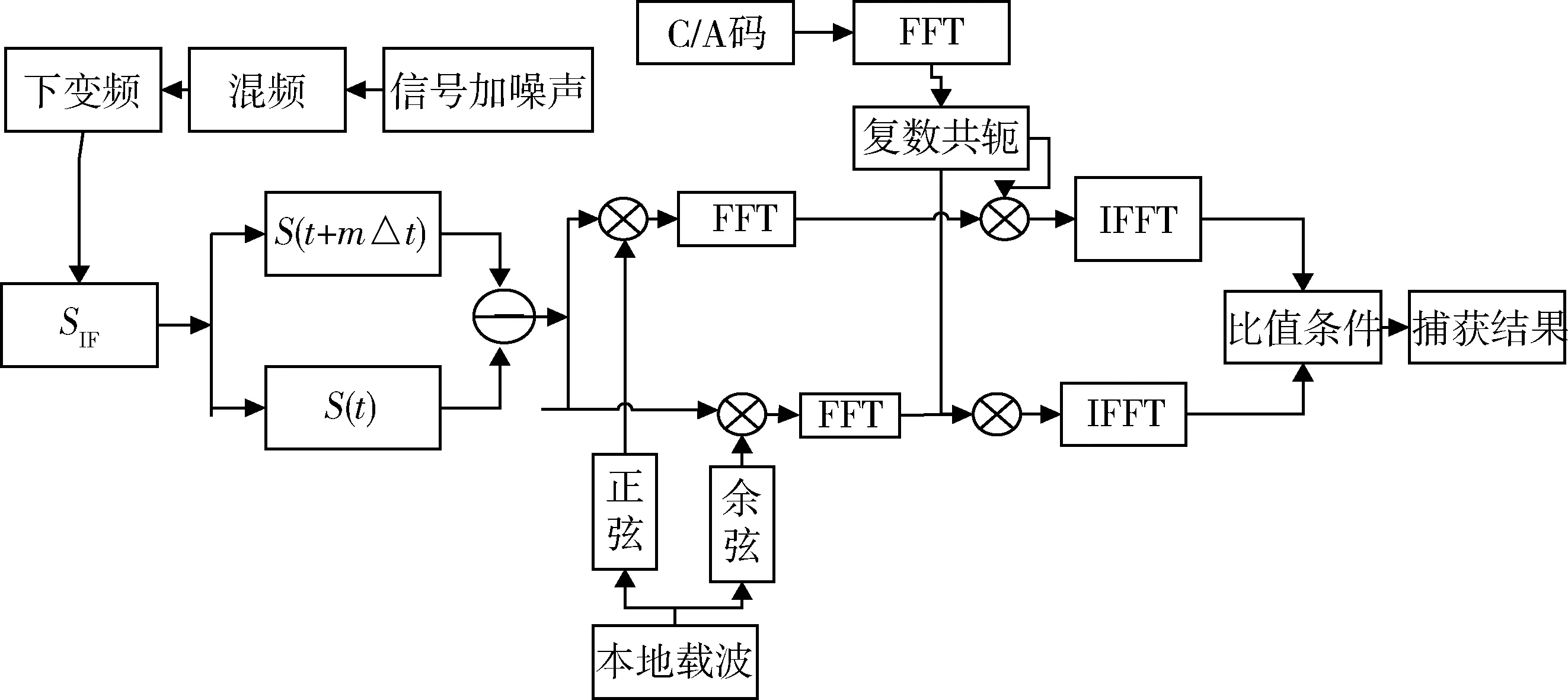
图1 捕获方案流程图

2.1 前差分的数字特征

式(4)假设的噪声模型属于正态分布，对于两个不同的码片集的信号来讲，两噪声互相独立。如果这两种信号做差，检验方法可以使用t检验。

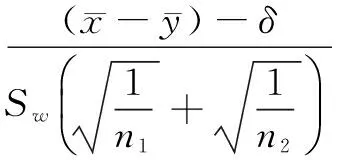
(5)

其中x、y分别是均值，n1，n2是样本的个数，Sw为：

(6)

因为可以使用t检验分布，所以有下面的计算公式：

(7)

其中，α是一个极小的数，因此算法可以有效地消除噪声，并且消除噪声的错误率不会超过常数α。

2.2 并行码捕获

对于卫星接收机来说，码的捕获过程就是一个本地序列与接收序列的相关过程，并行码捕获次数将由29×38 192次减少为只在频率维度上完成29次搜素。

如图1所示，数字中频信号分别在I、Q支路上与载波的正弦、余弦混频后，再将混频结果的复数形式i+j×q进行傅里叶变换。将变换结果与C/A码的傅里叶变换的共轭值相乘，再将得到的结果进行反傅里叶变换。这时，将得到在时域上的相关结果，对这个结果进行判断信号是否有效。

(8)

其中，H(-K)是H(K)的共轭。所以，时域上的相关运算相当于离散傅里叶在频域行做乘积运算。一旦接收机接收到傅里叶的反变换的值，接下来就是信号的检测，在所有的搜素单元中寻找到有效的卫星信号。

2.3 比值法

目前比较经典的方式有两种，一种是相关值累积值与一个固定的值进行比较，另一种是相关累积值的最大值和次最值的比值与一个阈值的比较。通过比值法，判决门限与噪声功率大小的耦合性变小。

3 仿真结果

在本文的研究中，使用的卫星信号是美国科罗拉多大学通过射频采集前端获得的两个样本：样本1：GPSdata-DiscreteComponents-fs38_192-if9_55.bin，其中采样频率是38.192 MHz，中频为9.55 MHz；样本2：GPS_and_GIOVE_A-NN-fs16_3676-if4_1304.bin，其中采样频率是16.367 9 MHz,中频是4.130 4 MHz。原始信号分别如图2、图3所示。

图2 样本1的原始信号

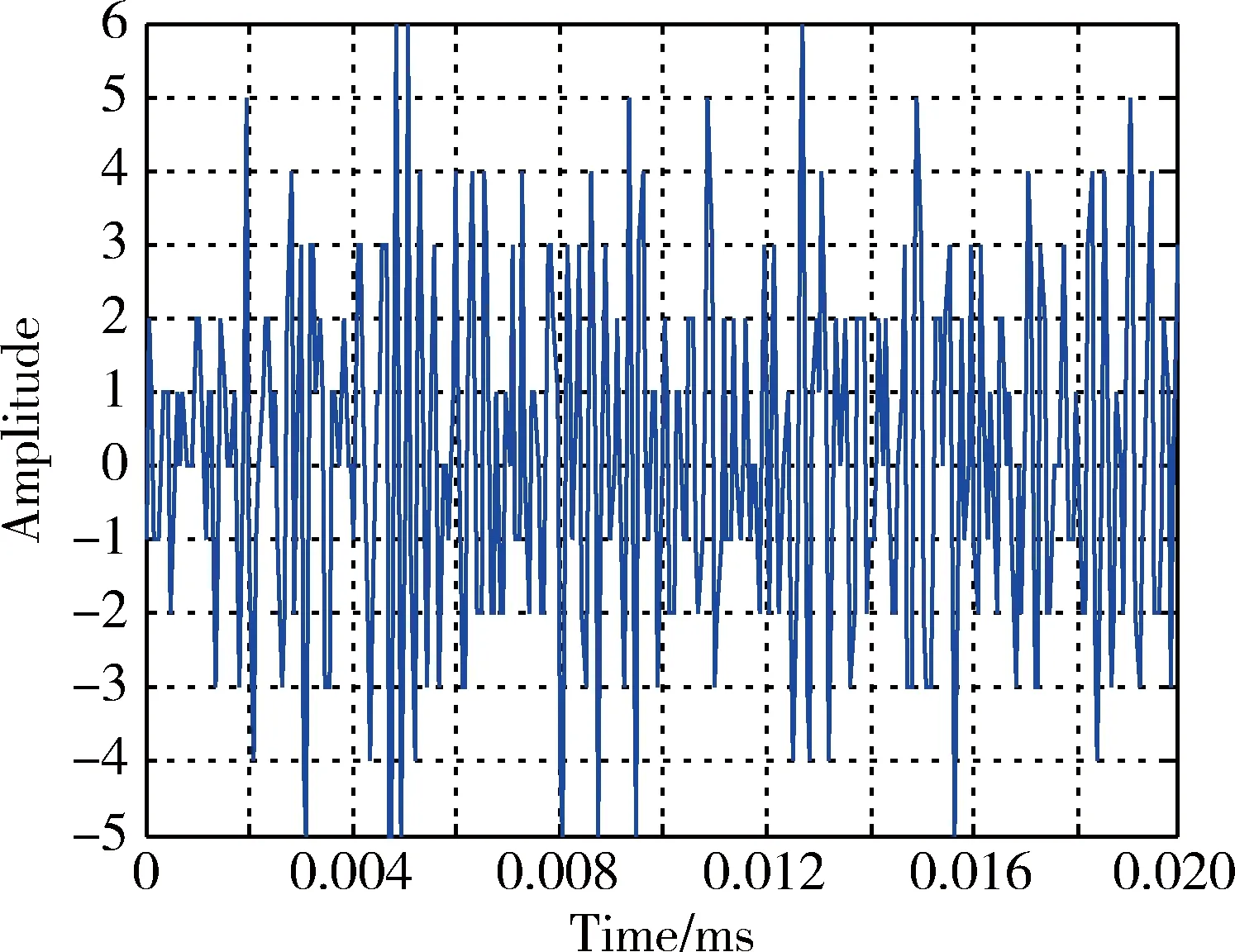
图3 样本2的原始信号

只有当接收机内部复制的载波和C/A码信号与接收的卫星信号相一致时，相关器的输出才会达到最大值，对于阈值方式判断捕获，如果最大的功率超过门限值，那么相应的该最大功率的复制信号参数值就是要捕获的卫星信号的参数值。

在这里使用样本1，通过MATLAB仿真，展示在各种噪声下的相关值的变化。在样本1上加上一定的高斯白噪声，其中噪声的均值为0、方差为9，会发现在噪声越来越大的情况下，如果门限太大，将难以检测到卫星，检测概率小；门限变小，将会出现虚警概率变高。

将图4与图5相比可以看出，外加噪声方差为9的相关值优势不再明显，同时，在图6与图7中使用样本2同样有这个问题。

采用《软件定义的GPS和伽利略接收机》附带的信号样本，并且使用书中经典算法进行仿真，结果如图8、图9所示。

图4 样本1在无噪声情况下的相关值

图5 样本1外加噪声方差为9的相关值

图6 样本2在无外加噪声情况的相关值

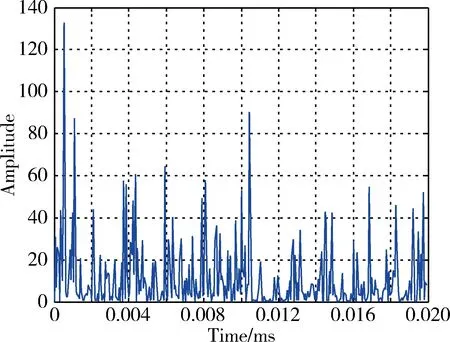
图7 样本2在外加方差为9的相关值

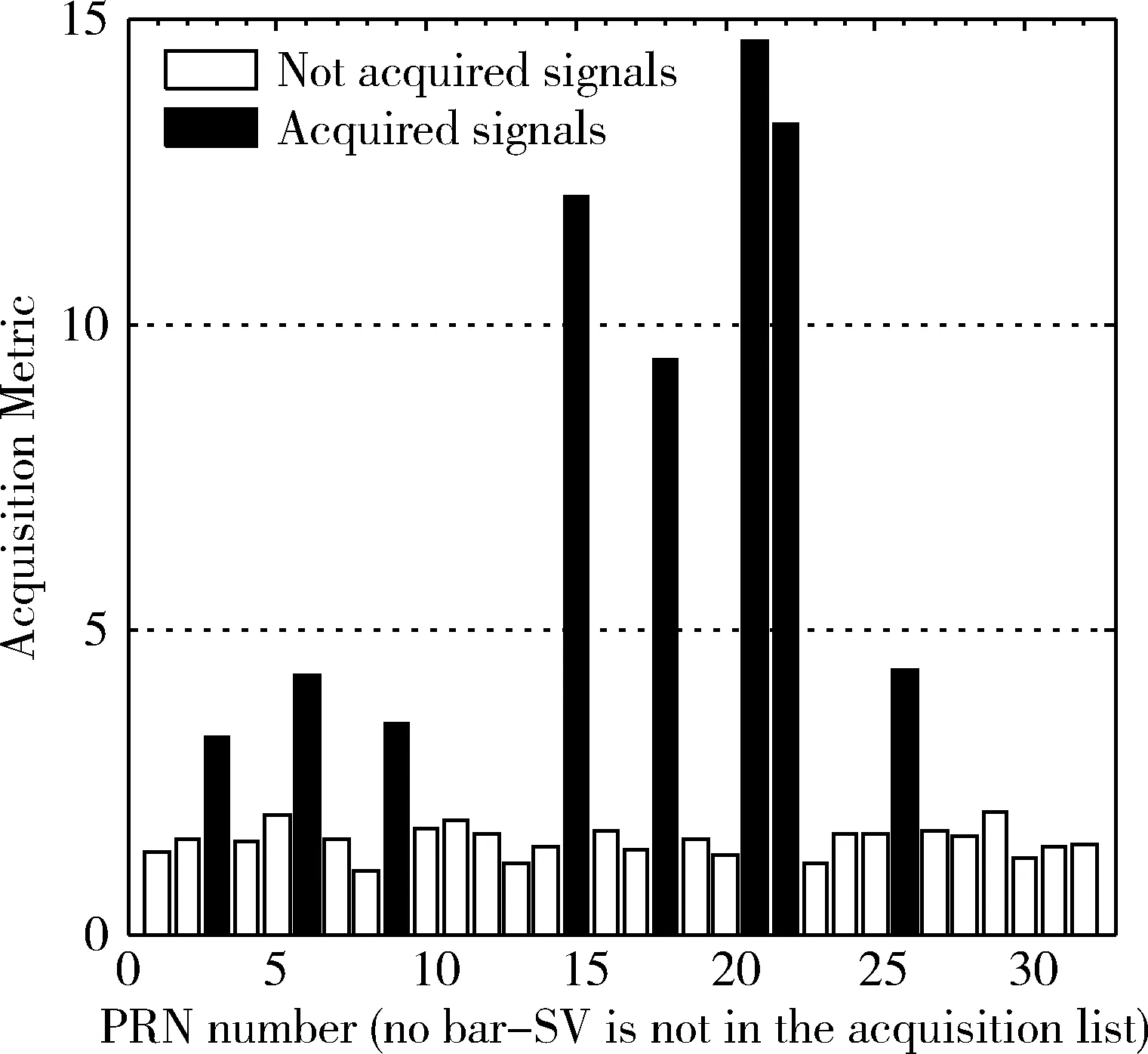
图8 样本1的捕获结果

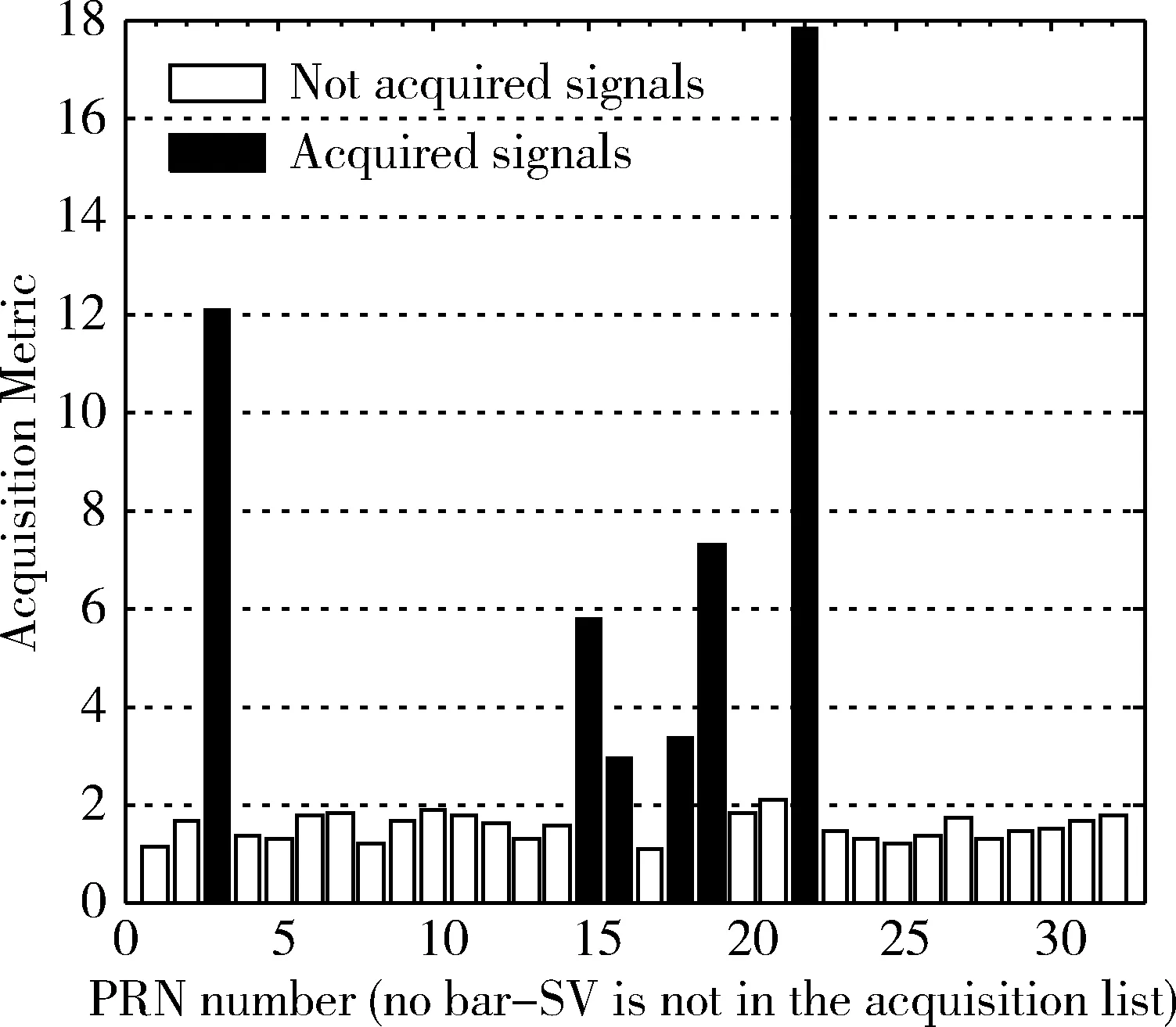
图9 样本2的捕获结果

从图8中可以看到，6、15、18、21、22、26的捕获峰值远远大于其他位置的卫星信号强度。

在图9中，3、15、18、22属于强信号。

通过以上对比，在接下来确定信号是否有效的算法中，信号的检测会使用比值法，用最大值与次最值的比值来判断信号的有效性。

以《软件定义的GPS和伽利略接收机》中的8颗卫星为标准，采取样本1进行仿真。在强弱信号混合的情况下，不同的门限值，不同的噪声方差，可以仿真出各种噪声下不同门限对应的捕获概率。如图10所示。

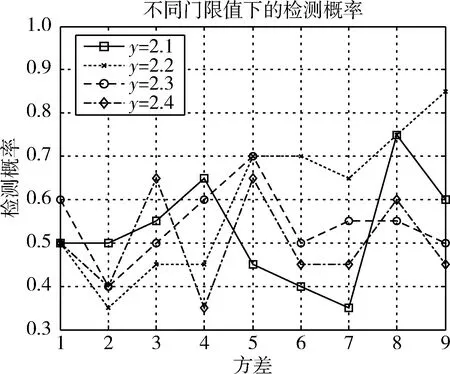
图10 各种信号下的检测概率

由图10可知，在信号比较大的情况下，门限值设定为2.2时捕获概率更大。同时，整体捕获概率不高，造成这种情况的原因是弱信号的存在，当前差分时，信号的消耗能量过大，造成了信噪比损失，解决这种问题的方式就是增加积分时间。

在这里，暂时不采取积分的算法，对强信号15、18、21、22外加3个弱信号卫星6、9、26，对7颗卫星的捕获概率进行检查，证明门限值为2.2的合理性。

图11 比值在2.2下的捕获概率

由图11可以看到，在门限判决比值为2.2的情况下，检测概率一直比较高，即在大部分情况下都可以捕获到卫星信号。

4 结论

卫星接收机在城市中移动时，噪声总是在不断地变化，这些噪声严重影响了卫星信号的捕获。通过MATLAB仿真可知，基于FFT的并行捕获技术，结合前差分技术和相干积分，在多噪声的情况下算法是有效的。其次，通过大量的仿真证明，噪声波动较明显时，判决门限的合理值大约是2.2。同时仿真表明，因为采用差分算法，造成了一些弱卫星信号的漏捕，即在开阔的情况下，捕获效果明显，在室内等环境，需要延长相干积分的时间来提高捕获概率。

[1] 谢钢.GPS原理与接收机设计[M].北京：电子工业出版社，2009.

[2] 唐光杰，张仁杰.GPS卫星捕获及跟踪算法研究[J].电子科技，2016,29(10): 33-35.

[3] 马若飞.GPS弱信号捕获算法研究及其在软件接收机上的实现[D].哈尔滨:哈尔滨工业大学，2010.

[4] 程川军.导航卫星弱信号相干-差分相干捕获算法的研究[D].大连:大连理工大学，2014.

[5] 韩帅.GNSS系统弱信号捕获方法研究与应用[D].哈尔滨:哈尔滨工业大学，2011.

[6] 李新山.基于差分相干的微弱GPS信号捕获与比特同步研究[D].成都:电子科技大学，2013.

[7] Lu Bidong, Zhong Jie, Zhao Minjian, et al. A near-far effect canceller for GPS high sensitivity receiver[C]. Proceedings of the 2012 IEEE/ION Position, Location and Navigation Symposium, 2012:341-346.

[8] Xiao Qidong, Peng Ao, Ou Gang. A novel weak signal acquisition scheme for Beidou nGEO satellite signals[C]. International Conference on Information Science and Technology, IEEE, 2015:83-88.

[9] 陈庆.微弱GPS/北斗系带信号捕获研究与实现[D].广州：暨南大学，2013.

Research on acquisition algorithm of GNSS signal under various noise

Cao Jun1, Yao Nan2, Jiang Shengming2

(1. College of Information Engineering, Shanghai Maritime University, Shanghai 201306, China;2. Shanghai Maritime University, Shanghai 201306, China)

In the current society, there is more and more uncertainty noise in the city. These noise can be incorporated into the effective satellite signal, failing to capture signal. The intensity of noise is fixed in many algorithms, which do not consider the situation that noise is variable. This paper is based on the parallel acquisition technique of Fast Fourier Transform, combined with the previous difference technique and coherent integration, to eliminate uncertainty effect. In addition, under the various noise, the reasonable value of the decision threshold has been obtained. The simulation results show that the algorithm can effectively capture the satellite signal and reduce the computational complexity.

uncertainty noise; previous difference; threshold; signal acquisition

TP92

A

10.19358/j.issn.1674- 7720.2017.13.020

曹军，姚楠，姜胜明.变化噪声下GNSS卫星信号的捕获算法的研究[J].微型机与应用，2017,36(13)：66-69.

2017-01-12)

曹军(1990-)，男，硕士，主要研究方向：卫星的捕获与定位。

姚楠(1983-)，通信作者，男，讲师，主要研究方向：无线电子研究。E-mail：nanyao@163.com。

姜胜明(1964-)，男，教授，主要研究方向：通信网络、结构、协议和算法。