中学数学欣赏初探
广东省顺德市德顺学校 何 杰
中学数学欣赏初探
广东省顺德市德顺学校 何 杰
数学作为一门逻辑性强与应用面广的基础学科,在人类的生活与工作的改革方面都发挥着巨大的作用。在数学教学的过程之中,不能够仅仅只注重知识的传授,还要让学生能够感受到数学美,进而产生出数学学习兴趣。本文主要就如何在中学数学中欣赏数学美进行探讨。
数学欣赏;学科德育;数学文化
党的十八大报告提出“立德树人是教育的根本任务”。数学是基础教育的核心课程,是培养人才的重要学科。数学对培养人的科学精神、思维方法、探索能力、思辨能力、量化思维、审美情趣等具有重要作用。笔者挖掘教学素材中显性和隐性的德育因子,寓数学欣赏于教学之中,以期达到数学文化的浸润和濡染的目的。
一、潜移默化,领悟数学的“真实美”
高中数学第一课,是对学生实施学科德育的最佳契机。教师要抓住这一机会,给学生学习上的期许和方法的指引,为学生学习数学营造良好的心理氛围。下面是课堂教学中的一个片段:
教师:初次见面,先考一考你们,请看这两组等式,你能联想到什么?这两组式子有何差异?
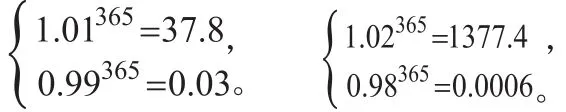
面对这样的问题,学生面面相觑,停留片刻后,一个大胆的女生自告奋勇地站起来说:“学习是一个积累的过程。”很睿智的回答!
教师补充:的确如此,不光学习,一个人的成长也是这样。中国有句古话,“勿以善小而不为,勿以恶小而为之”。这样一组简单对比的数学式子,真实地反映出量变引起质变的哲理。如果故步自封,不思进取,则原地踏步,人生就永远是“1”;如果每天前进一点点,向上一点点,向善一点点,假以时日,将会产生意想不到的惊喜;倘若每天自甘堕落,自暴自弃,人生时光消耗殆尽而毫无意义。
说完之后,同学们不由自主地都鼓掌了,说明两个式子在他们的心底都激起了涟漪。高中阶段是一个人习惯养成与思维成型的关键期,开学第一课,我并没有立即进入新课,而是通过这样一组指数式的呈现进行意识的熏陶,并鼓励学生誊写在笔记本的扉页上,激励自己,聚沙成塔,积流成河。
二、旁征博引,漫溯数学的“奇异美”
无论在课程设置、教材处理还是教学过程当中,教师都要对数学有一个横向的透视和纵向的对比。“数学不只是做题”,数学在教学中力求呈现数学动态统一的、有机关联的、鲜活生动的、具有探索性特征的科学和文化形象,而不是固定不变的、僵化教条的、片段局部的、彼此分割的知识点和方法库。
以勾股定理为例。对它的教学,是数学欣赏的很好素材,是数学文化渗透的绝佳载体。首先是直观之美:赵爽弦图、勾股树、与外星人做无文字交流之图,简洁明快,赏心悦目。其次是内涵之美:条件仅仅是直角三角形,却有直角边平方之和等于斜边的平方。它还是几何、代数、三角交汇之中心,细细琢磨,体现了和谐之妙、智慧之光。再次是人文之美:勾股定理在历史长河中,是迄今为止拥有最多证明方法的定理,显示了人类文明的共同追求。最后则是理性之美:好的数学一定是具有拓展、变形、升华的发展通道。勾股定理的触角伸向勾股数研究,以至联系到著名的费马大定理:当n≥3时,方程无整数解。这一定理于1637年由“业余数学家之王”——费马提出来,直到1995年才由Andrew Wiles和Richard Taylor共同解决。普林斯顿大学的Andrew Wiles在自家的阁楼上秘密攻关7年后,1994年,他在剑桥的牛顿数学研究所宣布证明了费马大定理,之后不久,有人发现他的证明有漏洞,由此开始了他炼狱般的最后一年:在世界数学家的瞩目下,艰难地修补了他证明中的漏洞。三百年间,有多少数学家付出了他们毕生的心血,做出了无偿的贡献,我们却能如此幸运地生长在这一年代,见证这一难题的破解。
在数学的发展历史上,许多杰出的数学家都给出了很多著名的猜想(如费马大定理、哥德巴赫猜想等),证明可能非常困难,但是寻找证明工具和证明思想的活动却大大地推动了数学的进展,发展了不胜枚举的数学思想和数学定理,费马定理也因此被誉为“会下金蛋的母鸡”。
三、巧夺天工,欣赏数学公式的“和谐美”
数学中不缺乏美,只是缺乏发现美的眼睛。教师在课堂教学中,要创设数学美的氛围,应设法引导学生去观察、认识、感悟,让学生的内心真实感受到数学的美。
这个等式是被数学家公认为最美的等式。其中,0,1,i,π,e是万紫千红的数的大花园中的5个常数,每一个常数的诞生都具有划时代的意义。1是人类认识的第一个数,标志着数学的诞生。有了1,就有了其他的数,就有了数学法则和数学结构,没有1的基础,就没有2以上的累进数;0诞生在印度,它是正负数的分水岭,是实数中唯一的中性数;0和1一起,在二进制和逻辑代数中,创造了电子时代的智能世界。π是圆周率的记号,数千年来吸引着无数的科学家为它贡献毕生的精力,祖冲之对它的领先研究为中华民族带来了荣耀,人类各个时代的数学水平都可以以它的精确度来衡量;感觉是不可思议的,跟初中所学的知识相悖,我们用虚数单位i来表示,这就涉及数系的再一次扩充——虚数,但是虚数其实并不“虚”;e则是自然对数的底数,对数的发明大大延长了天文学家的寿命。e和π一样,是无法计算出他们的准确值的,都是无理数,又是超越数。
奇妙而有趣的是,欧拉以其惊人的天赋和敏锐的分析,将这五个元素只通过简单地加号和等号和谐地统一在一起了,这是自然界的神奇和人类智慧的综合产物,是数学中的一大杰作。这个案例的设计,意在吸引他们在数学知识的海洋中学会去发现与探索,从而达到以美育情,以情启智的教育目的。
数学学习,从表层意义上来讲,是知识的学习,以知识的接受为最基本的要求,任何人都不可否认知识的力量。从深层意义来说,是思想、精神和方法的传承与运用,数学中蕴含着丰富的文化价值,影响人们的思维方式、智力发展、审美情趣和伦理道德,这也是数学教育隐性价值的重要体现。
[1]数学课程标准研制组.《普通高中数学课程标准(实验)》解读[M].南京:江苏教育出版社,2004.
[2]张奠宙.数学欣赏:一片等待开发的沃土[J].中学数学教学参考:上旬,2014(1):3-6.
[3]陈木法.数学的进步[J].数学通报,2012(9):1-6.
[4]任勇.你能成为最好的数学老师[M].上海:华东师范大学出版社,2011.

