复数的运算技巧
山东省寿光现代中学 任彦旭
复数的运算技巧
山东省寿光现代中学 任彦旭
复数的运算种类虽多,但各种运算方式间有联系,最本质的运算方式就是代数形式的运算。多样性的运算使得我们研究复数问题时有多种可考虑的途径,以便从中选择较好的方式,运用常用的结论或者利用数学思想方法来解题,可以简化运算。
一、整体角度巧转化
例1 已知z=2-i,则z6-3z5+z4+5z3+2=________。
分析:如果直接把z=2-i代入,运算起来比较繁杂,而根据题目条件,通过整体角度来转化,方法巧妙,运算快捷。
解析:由于z=2-i,则有(z-2)2=(-i)2=-1,即z2-4z+5=0,
所以z6-3z5+z4+5z3+2=(z2-4z+5)(z4+z3)+2=2,故填2。
点评:从整体角度思考,巧妙利用z=2-i转化为(z-2)2=(-i)2=1,即z2-4z+5=0,再通过因式分解来处理即可快捷求解。运算时抓住整体,可以高屋建瓴。
二、常见公式妙应用
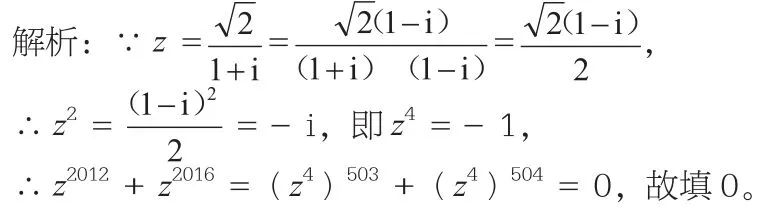
点评:抓住常见公式有时是解决此类复数问题的关键,常见的复数运算公式有:(1)i的乘方:i4k=1,i4k+1=i,i4k+2=-1,等。运算时利用常见公式,可以简化过程,提升速度。
三、分类讨论巧解决
分析:通过复数关系式的转化,化简为in·[(1+i)+(-1)n·(1-i)]=2,结合n的奇偶数取值情况分类讨论,进而求解最小正整数n。
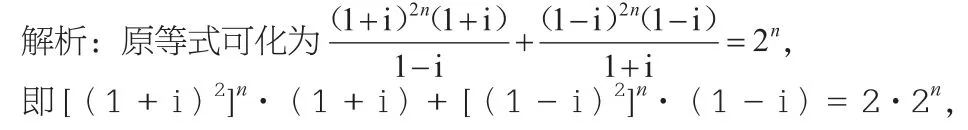

点评:在解决复数问题中,涉及复数的分类、参数的取值等相关问题时,往往通过分类讨论,结合复数运算来分析与求解。运算时结合分类讨论,理清思路,拓展思维。
四、几何意义妙转化
分析:通过复数几何意义的转化,把求解对应复数的模的问题转化为解决平面图形的相关线段的长度问题。
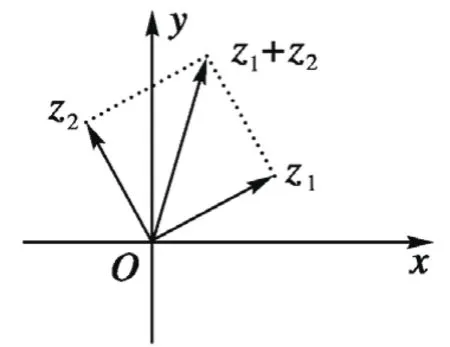
点评:从复数的几何意义入手来转化,把代数运算问题几何化,结合复数的几何意义,利用直观平面几何图形来分析与处理。运算时利用复数的几何意义,可以化代数问题为几何问题,通过几何直观来处理。
复数运算中,关键是抓住复数的加、减、乘、除、乘方等运算,结合题目条件,利用整体角度、常见公式、分类讨论、几何意义等运算技巧加以综合与处理,达到快捷求解、正确运算的目的。

