考虑电压畸变的电气弹簧功率因数校正策略研究

张骕骦，丘东元，张 波

（华南理工大学电力学院，广州 510640）

考虑电压畸变的电气弹簧功率因数校正策略研究

张骕骦，丘东元，张 波

（华南理工大学电力学院，广州 510640）

为了解决新能源发电系统并网所带来的电力系统稳定问题，提出了新型电力电子装置“电气弹簧”。目前电气弹簧功率因数校正PFC策略是在电网电压为理想正弦波的前提下提出的，不适用于电网电压含有较大谐波分量的实际场合，如整流装置和电弧炉等非线性负荷比重比较大的工厂配电网。为此，在详细分析电气弹簧功率因数校正原理的基础上，提出了一种考虑电网电压畸变的功率因数优化控制策略，通过在电流控制环中加入电流谐波环，将电流畸变率控制在规定范围内，从而在限制电流畸变率的同时，实现电气弹簧的最大功率因数校正功能。最后给出了仿真结果，验证了所提功率因数校正策略的可行性。

电气弹簧；电压畸变；功率因数校正；dq变换

随着越来越多的间歇性新能源发电系统并网，电网的稳定运行面临越来越多的挑战。电网波动不仅会使电气设备受到严重损坏，严重时还可能导致整个电网崩溃。为了解决新能源发电系统并网带来的功率平衡等问题，研究人员提出了多种电力负荷管理方法，如负荷调度[1]、实时电价[2]、电力负荷控制[3-4]等，但这些方法很难实现电力负荷管理的实时性。电能存储[5]虽然可以实现实时功率平衡，但大功率储能系统价格昂贵，且废弃的电化学电池、超级电容等还会带来新的环境污染问题。

为了解决新能源发电系统带来的电网稳定问题，一种新型电力电子装置“电气弹簧”被提出[6]，电气弹簧以胡克定律为基础，用以稳定新能源发电系统，有助于大规模新能源并网。电气弹簧可以内嵌于电热水器、冰箱等非关键负载中，当电网功率波动时，电气弹簧实时改变其端电压，使与其串联的非关键负载功率随着电网功率动态调整，进而维持功率平衡。换言之，电气弹簧将供电不稳带来的电网波动完全转移到非关键负载中，避免关键负载故障而导致经济损失及人命伤亡。电气弹簧可以实时地调整电力负荷，不需要集中控制，同时也会减少储能设备的投入，在稳定未来智能电网方面有很大的潜力[7-10]。除了稳压功能之外，电气弹簧还具有谐波补偿[11]、三相功率不平衡抑制[12-13]以及功率因数校正 PFC（power factor correction）[14]等功能。

随着电力电子技术的发展，越来越多的非线性负载（如整流装置等）和新能源发电系统并入电网，电网中的谐波问题也越来越严重[15-17]。文献[18]对不同电压等级的谐波进行了分析，说明各级电网都含有电压谐波分量，理想化的正弦电压并不存在。因此，电网电压谐波是普遍存在的，特别是在非线性负载比例较大的厂区，谐波电压含量更大[19]。而文献[14]提出的电气弹簧功率因数校正策略是在电网电压为正弦波的情况下提出的，故校正后的电流是与电网电压同相位的正弦波。当电网电压含有谐波时，如果电流仍是正弦波的话，对应的功率因数达不到最大值。我国70%以上的年用电量为工业用电，在按功率因数调整电费的收费方案中，功率因数越高用电成本越低[20]。因此，提高功率因数有利于降低用电成本。

本文首先阐述了理想电网下电气弹簧功率因数校正原理及现有控制策略；然后提出了电网电压畸变情况下提高功率因数的控制方法；最后用仿真软件MATLAB/Simulink验证了本文所提控制方法的有效性。

1 理想电网下电气弹簧功率因数校正原理

图1 电气弹簧在电网中的连接方式Fig.1 Connection of electrical spring in power grid

电气弹簧在电网中的典型连接方式如图1所示。其中电气弹簧和非关键负载ZNC串联组成 “智能负载”，智能负载和关键负载ZC并联接入电网。如果新能源发电系统输出功率波动，电气弹簧调整端电压ves，使非关键负载ZNC端电压vo和其消耗功率跟随输出功率波动。电气弹簧通过实时调节输出电压ves，进而控制输出无功功率和/或有功功率的大小，把新能源并网带来的电网波动全部由非关键负载承担，保证了关键负载ZC的供电电压稳定，实现了电源与负载间的动态平衡。

功率因数校正PFC是电气弹簧的重要功能之一，其可以减少电源无功功率交换，提高电源用电效率，降低线路损耗。含电气弹簧的系统等效电路如图2所示。

图2 含电气弹簧的系统等效电路Fig.2 Equivalent circuit of electric spring system

图2中，线电流is表示为

式中：is为线电流；vs为公共节点电压；ves为电气弹簧端电压；ZNC为非关键负载阻抗；ZC为关键负载阻抗。则电压源电压vg和vs的关系为

式中，ZS为线路阻抗。 联立式（1）、式（2），得到 is、vg和ves的关系，即

由式（3）知，改变电气弹簧端电压ves的幅值和相位可以控制电流is的幅值和相位，通过合适的控制策略，控制电流is为与电源电压vg同相的正弦波，从而获得单位功率因数。但式（3）中，is的相位和ves幅值、相位之间存在耦合关系，需要对式（3）进行变换，以实现解耦控制。

本文通过坐标变换实现式（3）的解耦，把所有相量分解为d轴和q轴分量，并选定参考相量为vg。若vg的q轴分量为0，为实现单位功率因数，则输入电流is的q轴分量也要为0。

由式（3）求得

式中，b1、b2、b3、b4均为常数。 联立式（4）～式（6）得

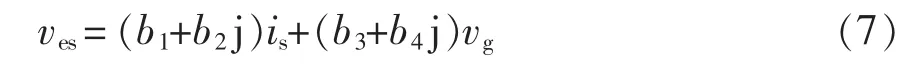
选择电压源电压vg作为dq变换参考信号，即vg=|Vg|∠0°为 d 轴，则式（7）通过 dq 变换为

由式（8）知，d轴和q轴并没有实现独立控制，d轴和q轴之间存在着耦合现象，需要采取解耦处理，消除d轴和q轴耦合影响。令

式中：kp和kI分别为比例和积分常数；和分别为电流在d轴和q轴的对应分量。对比式（8）和式（9）得

由式（10）可知，电流is在d轴和q轴为独立控制没有耦合，实现了d轴和q轴电流解耦。由式（9）对应的控制框图如图3所示，如果电流is的q轴参考值设为0，则补偿之后的电流is只含有d轴分量，即与参考向量vg保持同相位，实现了功率因数校正功能[21-22]。

图3 不考虑电压谐波的电气弹簧PFC控制框图Fig.3 PFC control block diagram regardless of the voltage harmonic

2 考虑电压畸变的电气弹簧功率因数校正策略

文献[23]提出了一种畸变电压下功率因数的计算方法，表示为

式中：P、S分别为有功功率和无功功率有效值；N为谐波总次数；Un为电压基波和电压各次谐波有效值n=0，1，…，N；In为电流基波和电流各次谐波有效值；U、I分别为电压、电流总有效值；cos φ2n+1为基波和各次谐波电压电流功率因数。

采用图3所示的电气弹簧功率因数校正策略，校正后的电流为和基波电压同相位的正弦波，根据式（11），得到校正之后的功率因数为

由式（12）知，如果电压畸变率越大，校正之后的功率因数越低，在谐波含量比较大的电网中，并不能实现功率因数的最大化。

分析式（11），如果谐波电压和电流满足以下关系

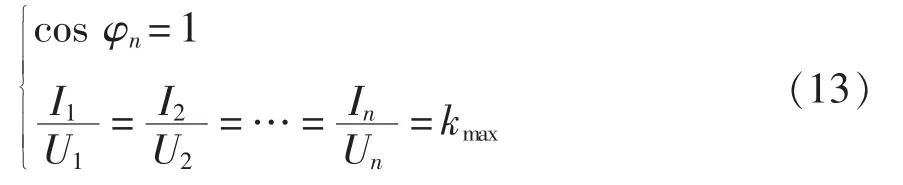
那么，畸变电网的功率因数PF=1，即基波、各次谐波电流和对应的基波、各次谐波电压同相位，且基波电压电流的比值与各次谐波电压电流比值相等，其中kmax为基波电流和基波电压比值。

但当电压畸变率比较大时，谐波电压变大，若保证功率因数为1，电流谐波也会大大增加，电流畸变率THDi可能超过规定值5%。为了保证THDi≤5%，且功率因数尽可能达到最大值，需要考虑以下3种情况。

情况1：当电压谐波畸变率THDu为0＜THDu＜5%时，由于电压谐波比较小，在实现单位功率因数校正的同时，电流谐波畸变率THDi在5%以下，即

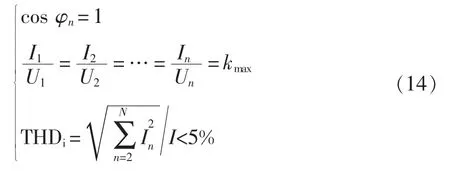
情况1下校正后的功率因数为

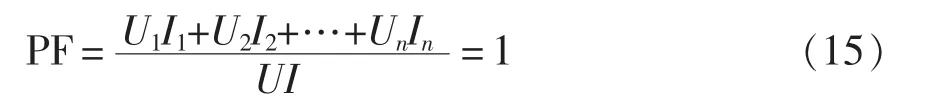
情况2：当电压谐波在THDu=5%时为临界状态，在实现功率因数校正的同时，THDi正好为5%。

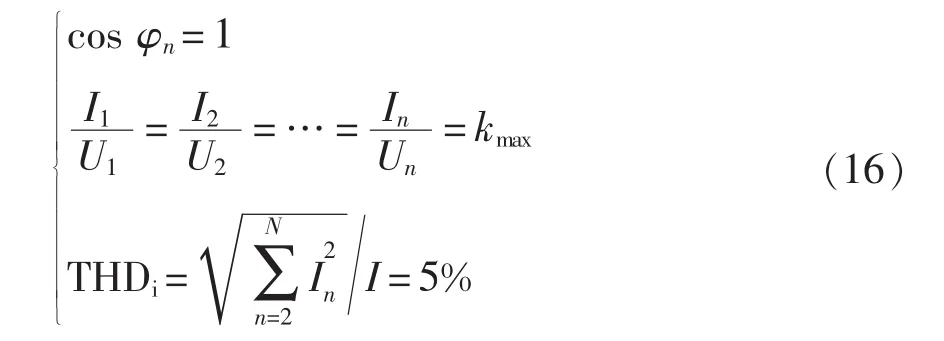
情况2下校正后的功率因数为

情况 3：当电压谐波在THDu＞5%时，如果要实现单位功率因数校正，那么THDi将会超过5%；因此，要在电流谐波不超标的前提条件下，实现功率因数的最大化，即满足如下条件：

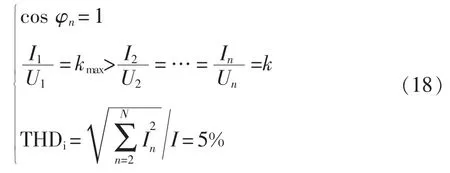
其中，k为常数。情况3下校正后的功率因数为

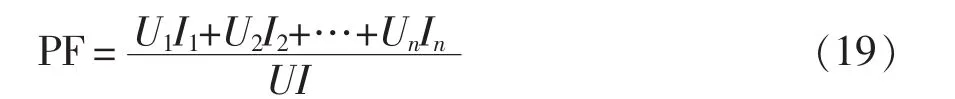
由于电压谐波 THDu＞5%，则

由式（18）中第3个等式得

代入到式（19）得

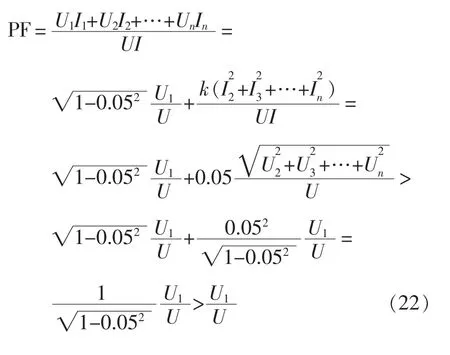
在上述3种情况下，采用传统控制策略和本文所提控制策略得到的电气弹簧功率因数校正结果如表1所示。由表可知，当电压谐波THDu≤5%时，传统控制策略中PF1=1，而本文控制策略可以保证校正后的PF2=1；当电网电压THDu＞5%时，PF1=。3 种情况下，PF2始终大于PF1，论证了控制策略的有效性。

表1 3种情况下功率因数校正结果比较Tab.1 Comparison of power factor correction results in three cases

根据式（14）、式（16）、式（18），在电压畸变情况下电气弹簧的功率因数校正控制框图如图4所示，对电网基波和谐波分别进行dq解耦控制，使基波和各次谐波电流的q轴分量为0，从而保证cos φn=1。确定基波电流is1作为基波电流d轴参考值，并通过以上3式计算出各次谐波电流分量的最大值作为各次谐波电流d轴参考值。

由图1可知，公共节点电压vs为

图4 本文所提电气弹簧PFC控制框图Fig.4 PFC control block diagram considering the voltage harmonic

分析式（23）知，通过控制电流is，可以调节公共节点电压vs，因此可以在实现功率因数校正的同时实现稳压功能。对比图4和图3的两种控制策略，本文提出的控制策略增加了一个电流谐波环，此谐波环使电网侧电流含有和电网电压相同的谐波分量，从而在保证输入电流畸变率THD≤5%的前提下，实现功率因数最大化。

3 仿真验证

使用Matlab/Simulink软件进行仿真，仿真电路如图5所示，以验证所提功率因数校正策略的有效性。设定谐波电压大于5%，令谐波电压源方程为

同时，为了验证电气弹簧具有稳压功能，用电流源模拟并网的新能源发电系统，额定状态下，新能源并网电流峰值为1.3 A，母线电压有效值维持在额定值vs-rms=220 V，通过调节电流峰值偏离额定值1.3 A便可模拟电网波动。

设置仿真参数如下：非关键负载阻抗为ZNC=88+j41=97∠25°Ω；线路电阻为 R1=R2=2 Ω，线路电感L1=L2=1 mH。0～0.5 s期间，电流源峰值为额定值1.3 A，公共节点电压为额定值；0.5 s时刻，由于新能源并网功率波动，电流源峰值达到6 A，电网电压随之发生波动；电气弹簧在1 s时刻投入工作，对比电气弹簧投入前后功率因数PF和和公共节点电压vs大小。

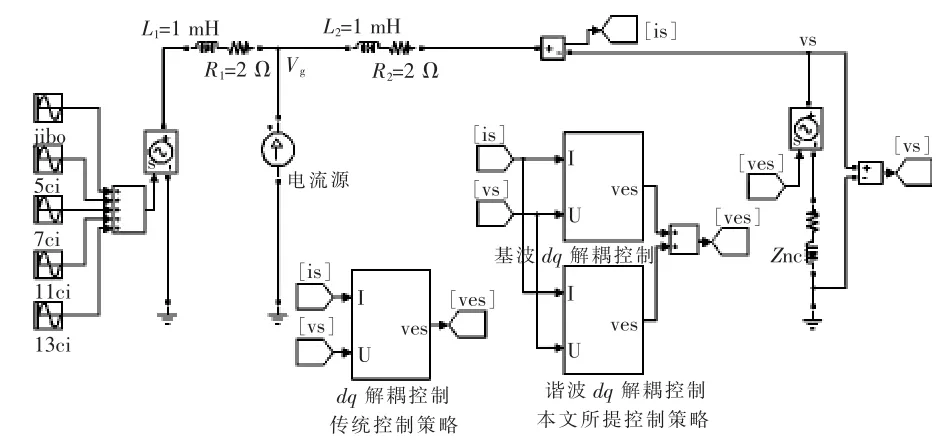
图5 电气弹簧仿真电路Fig.5 PFC simulation circuit of electrical spring

3.1 未投入电气弹簧时

未投入电气弹簧时的仿真结果如图6所示。图（a）中光伏并网电流ig峰值大小于0.5 s时刻偏离额定值1.3 A；由于负载为阻感性负载，由图6（b）可知，此时功率因数为PF=0.881，电压vs和电流is波形图如图6（c）所示；由于0.5 s时刻新能源波动，导致公共节点电压vs有效值为vs-rms=226.1 V，高于额定值220 V，如图6（d）所示。可以看到未加入电气弹簧时，负载侧功率因数比较低，电压也发生波动，对电网造成危害。

图6 未投入电气弹簧的系统仿真结果Fig.6 Simulation results without electric spring

3.2 采用传统PFC控制策略

1 s之后电气弹簧参与工作，采用图3所示的无谐波电流环的传统控制策略，系统的仿真结果如图7所示。由图7（a）可知，电气弹簧参与功率因数校正后的PF=0.966；电流is的傅里叶分析如图7（e）所示，可见功率因数校正之后，电流is基本不含有谐波；电气弹簧工作电压如图7（c）所示，可见电气弹簧通过调整端电压ves使电流is为正弦波，并与畸变电压vs同相位；图7（d）为电气弹簧工作后公共节点电压vs有效值，可见电压有效值重新回到额定值220 V，实现了稳压的功能。

图7 传统PFC控制策略仿真结果Fig.7 Simulation results of traditional PFC control strategy

3.3 采用本文所提PFC控制策略

当电气弹簧采用图4所示的控制策略，系统仿真结果如图8所示。由图8（a）可见，功率因数PF=0.98；电流is谐波分量为4.98%，满足规定的要求。通过增加电流谐波环，功率因数较传统控制策略提高0.014。功率因数虽然提高较小，但在工厂供配电系统中，功率因数大小决定电价，而且工业用电量在全国总用电量占有非常大的比重，很小的功率因数提升都可以节省很大一部分用电成本。

图8 本文所提PFC控制策略仿真结果Fig.8 Simulation results of the proposed PFC control strategy

4 结语

为了尽可能提高畸变电网下的功率因数，本文提出了在电气弹簧PFC控制策略中增加电流谐波环的新型控制策略，校正之后的电流含有和电压相同次数的谐波分量，并可以保证电流畸变率不超过所规定的5%，尽可能提高功率因数。理论分析和仿真结果表明，采用本文所提的PFC控制策略能取得比传统控制策略更好的功率因数校正效果。

[1]Mohsenian-Rad A H,Wong V W S,Jatskevich J,et al.Autonomous demand-side management based on game-theoretic energy consumption scheduling for the future smart grid[J].IEEE Transactions on Smart Grid,2010,1（3）：320-331.

[2]Conejo A J,Morales J M,Baringo L.Real-time demand response model[J].IEEE Transactions on Smart Grid,2010,1（3）：236-242.

[3]Lee S C,Kim S J,Kim S H.Demand side management with air conditioner loads based on the queuing system model[J].IEEE Transactions on Power Systems,2011,26 （2）：661-668.

[4]周潮，邢文洋，李宇龙.电力系统负荷预测方法综述[J].电源学报， 2012， 10（6）：32-39.

Zhou Chao,Xing Wenyang，Li Yulong.Summarization on load forecasting method of electrical power system[J].Journal of Power Supply,2012,10（6）：32-39（in Chinese）.

[5]林海雪.现代储能技术应用概况及展望[J].电源学报，2015，13（5）：34-40.

Lin Haixue.Applying situation and prospects of modern energy storage technology[J].Journal of Power Supply,2015,13（5）：34-40（in Chinese）.

[6]Hui S Y R,Lee C K,Wu F F.Electric springs-a new smart grid technology[J].IEEE Transactions on Smart Grid,2012,3（3）：1552-1561.

[7]Lee C K,Cheng K L,Ng W M.Load characterization of electric spring[C].Energy Conversion Congress and Exposition（ECCE）,2013 IEEE,2013：4665-4670.

[8]Tan S C,Lee C K,Hui S Y.General steady-state analysis and control principle of electric springs with active and reactive power compensations[J].IEEE Transactions on Power Electronics,2013,28（8）：3958-3969.

[9]Lee C K,Tan S C,Wu F F,et al.Use of Hooke's law for stabilizing future smart grid-the electric spring concept[C].Energy Conversion Congress and Exposition（ECCE）,2013 IEEE,2013：5253-5257.

[10]Lee C K,Chaudhuri B,Hui Y H.Hardware and control

implementation of electric springs for stabilizing future smart grid with intermittent renewable energy sources[J].IEEE Journal of Emerging and Selected Topics in Power Electronics,2013,1（1）：18-27.

[11]Shuo Yan,Tan Siew-Chong,Lee C K,et al.Electric spring for power quality improvement[J].Applied Power Electronics Conference and Exposition（APEC）,2014 Twenty-Ninth Annual IEEE,2014：2140-2147.

[12]Shuo Yan,Tan Siew-Chong,Lee C K,et al.Reducing threephase power imbalance with electric springs[C].Power Electronics for Distributed Generation Systems（PEDG）,2014：24-27.

[13]Shuo Yan,Tan Siew-Chong,Lee C K,et al.Electric springs for reducing power imbalance in three-phase power systems[J].IEEE Transactions on Power Electronics,2015,30（7）：3601-3609.

[14]Kanjiya P,Khadkikar V.Enhancing power quality and stability of future smart grid with intermittent renewable energy sources using electric springs[C].2013 International Conference on Renewable Energy Research and Applications,2013：918-922.

[15]王群，姚为正，刘进军，等.谐波源与有源电力滤波器的补偿特性[J].中国电机工程学报，2001，21（2）：16-20.

Wang Qun,Yao Weizheng,Liu Jinjun,et al.Harmonic source and compensation characteristics of active power filters[J].Proceedings of the CSEE,2001,21（2）：16-20 （in Chinese）.

[16]李达义，陈乔夫，贾正春.电力系统谐波源的种类和滤波方法综述[J].电气传动， 2005， 35（12）：3-7.

Li Dayi,Chen Qiaofu,Jia Zhengchun.Types of harmonic source and their filtering appraches[J].Electric Drive,2005,35（12）：3-7（in Chinese）.

[17]李芬，邹云屏，邓春花，等.交流电子负载谐波分析与抑制[J].电源学报， 2010， 8（1）：8-14.

Li Fen,Zou Yunping,Deng Chunhua,et al.Analysis and suppression of harmonics in AC electronic load[J].Journal of Power Supply,2010,8（1）：8-14（in Chinese）.

[18]任元，陈宝喜.电网各电压等级的谐波电压[J].中国电力，1994（8）：38-40.

Ren Yuan,Chen Baoxi.Harmonic voltage of each voltage grade of power network[J].Electric Power,1994（8）：34-40（in Chinese）.

[19]廖兴建.工厂的谐波抑制[J].电工技术，2007（7）：21-22.

Liao Xingjian.Harmonic control in factory[J].Electric Engineering,2007（7）：21-22（in Chinese）.

[20]童英杰.论功率因数调整电费改革[J].中国新技术新产品， 2010（19）：158-158.

Dong Jieyin.The power factor adjustment charge reform theory[J].New Technologies and New Products of China,2010（19）：158-158（in Chinese）.

[21]Kanjiya P,Khadkikar V,Zeineldin H H.Achieving maximum possible power factor with single-phase shunt active power filter under distorted supply condition[C].2012 IEEE 5th Power India Conference,2012：19-22.

[22]Ciobotaru M,Teodorescu R,Blaabjerg F.A new single-phase PLL structure based on second order generalized integrator[C].Power Electronics Specialists Conference,2006.PESC'06,37th IEEE,2006：18-22.

[23]李绍铭，刘红锐.电网畸变下功率因数的定义[J].重庆大学学报， 2008， 31（4）：413-416.

Li Shaomin,Liu Hongrui.Power factor definition under power network deformation[J].Journal of Chongqing University,2008,31（4）：413-416（in Chinese）.

Power Factor Correction Strategy of Electric Spring Under Voltage Distortion

ZHANG Sushuang,QIU Dongyuan,ZHANG Bo
（School of Electric Power,South China University of Technology,Guangzhou 510640,China）

In order to make the power grid system operate stably,the new power electronic devices “Electric Spring”has been presented to achieve regulation,harmonic compensation,power factor correction（PFC） and other functions.The PFC study of electric spring regarding the power grid as an ideal sinusoidal voltage,is not suitable for the actual situation of the large harmonic components of the grid voltage,particularly in the large factories where the proportion of non-linear loads is relatively large such as fairing and electric arc furnace.In this article,the principle of the electric spring power factor correction is analyzed detailedly.Considering the grid voltage distorts,the optimal control strategy is proposed to add the current harmonic loop into current control loop and to control the current distortion rate remaining within the specified range,which ensures the current distortion,and while achieves the maximum power factor correction of the electric spring.The simulation result verifies the feasibility of the proposed strategy of PFC.

electric spring;distorted supply;power factor correction（PFC）;d-q transformation

张骕骦

张骕骦（1990－），男，通信作者，硕士，研究方向：电力电子与电力传动，E-mail：37 1196389@qq.com。

10.13234/j.issn.2095-2805.2017.4.97

TM46

A

2015-12-04

国家自然科学基金资助项目（51277079）

Project Supported by National Natural Science Foundation of China（51277079）

丘东元（1972－），女，博士，教授，研究方向：电力电子与电力传动，E-mail：epdyqiu@scut.edu.cn。

张波（1962－），男，博士，教授，研究方向：电力电子与电力传动，E-mail：epbhang@scut.edu.cn。