组合证券投资决策的随机规划模型及其等价算法

刘晓娟

(上海电力学院 数理学院, 上海 200090)



组合证券投资决策的随机规划模型及其等价算法

刘晓娟

(上海电力学院 数理学院, 上海 200090)

引入概率测度和置信水平,给出了组合证券投资决策的随机规划模型.并针对风险证券投资组合收益率随机变量的分布情况,分别给出了模型的不同解法,即传统的优化理论算法和等价性线性规划算法.数值算例表明,该算法具有简便、可行、有效的特点,更具有实际的应用价值.

证券投资选择; 随机规划模型; 概率测度; 线性规划

1952年,MARKOWITZ Harry发表了一篇题为“投资组合选择”的论文,阐述了如何利用投资组合创造更多的可供选择的投资品种,从而在一定风险水平下取得最大可能预期收益率,开创了现代金融数学的先河,被誉为20世纪华尔街的第一次金融革命.不过在当时的条件下,该模型的计算技术复杂,并且有很多实际的限制,譬如随机参数要求对称分布;效用函数为二次函数;要求投资者为理性的,要按照“风险宁少勿多,收益宁多勿少”的原则进行投资等.

另外,社会经济系统(尤其是证券、期货等风险投资)作为复杂的开放系统,通常具有多维性、非线性、多准则性的典型特征.在现实生活中,投资者为了获得更高的收益而并非完全按照理性原则来进行投资决策.文献[1]至文献[9]提出了基于概率准则的随机系统组合投资模型,理论上克服了传统证券收益率向量必须服从(混合)正态分布的局限性.其中,文献[3]至文献[5]在假设证券收益率服从正态分布的前提下,主要研究了概率准则组合投资模型的确定性等价类解法,将其在一定条件下转化为整数规划、非线性或者动态规划等最优化解法,研究了最优解的存在性以及求解公式等;文献[6]至文献[8]在假设证券收益率服从任何分布的情况下,给出了概率准则组合投资模型,利用遗传算法,给出了模型的近似模拟解等.但考虑到遗传算法作为智能优化算法中较为成熟的算法,一方面能依照自然界中适者生存、优胜劣汰的自然进化规则,处理不确定的优化技术,具有适应性强、鲁棒性好的特点;但另一方面,遗传算法极易陷入局部极值,而且交叉算子、遗传算子等参数的选择比较繁琐.文献[9]设计了一种基于万有引力搜索算法的智能优化算法,较好地解决了遗传算法的缺陷.但是这些智能算法迭代次数较多,算法步骤设计较为复杂.文献[10]构建了机会约束下使投资风险最小的投资组合选择模型,并讨论了其有效边界、投资策略显式解等问题.

考虑到在发生不利情况时,所作决策可能不满足约束条件,因此本文引入概率测度和置信水平,给出了组合证券投资决策的随机规划模型,并针对风险证券投资组合收益率随机变量是否服从正态分布的情况,分别给出了模型的不同解法,包括传统的优化理论算法和等价的线性规划算法.该算法简便、可行、易于实现,更具实际指导意义.

1 模型的建立

假设证券市场上有n种风险证券,记为s1,s2,s3,…,sn,这n种风险证券组成了一个投资组合,其组合收益率为随机向量ξ=(ξ1,ξ2,ξ3,…,ξn)T,记投资组合在风险证券上的投资比例向量为x=(x1,x2,x3,…,xn)T,则xiξi为风险证券si的收益率.

2 模型的求解

根据风险证券投资组合收益率随机向量ξ的分布情况,可分为以下两种情况来求解模型1.

2.1 正态分布情形

如果风险证券投资组合收益率随机变量ξ=(ξ1,ξ2,ξ3,…,ξn)T服从正态分布N(μ,Q),其中μ=(μ1,μ2,μ3,…,μn)T,Q为正定对称矩阵,则上述随机规划模型1可化为下面的确定性等价类:

从而约束条件Pr{xTξ≥R}≥α可转化为:

则模型1可化为模型2,即:

因此,可以用传统的优化理论方法进行求解,该情形在文献[3]和文献[5]中已基本解决.

2.2 非正态分布情形

如果风险证券投资组合收益率随机向量ξ不服从正态分布,那么就很难转化为上述确定性等价类,也不能用传统的优化理论方法来求解.虽然借助于遗传算法、万有引力搜索算法等智能优化算法可以得到近似最优解,但值得注意的是,遗传算法中的交叉算子和变异算子的选择比较复杂,其他智能优化算法中参数的选择也具有很大的不确定性.

因此,下面给出一种简便的等价性线性规划算法,该算法原理清晰,步骤简洁易操作.

步骤2 分别在这Tj(j=1,2,3,…,K)个子集上建立如下的线性规划模型3:

解这K个等价性线性规划模型,得出K个最优解分别记为x(1*),x(2*),x(3*),…,x(K*);

步骤3 将这K个最优解分别代入目标函数,则使得目标函数值最大的那个解x(j*)就是模型1的最优解.

步骤4 若上述过程无解,则需重新调整参数R和α,重复上述步骤,直至求得最优解.

3 数值算例及结果分析

假设7种证券的期望收益率和风险系数分别如表1所示.

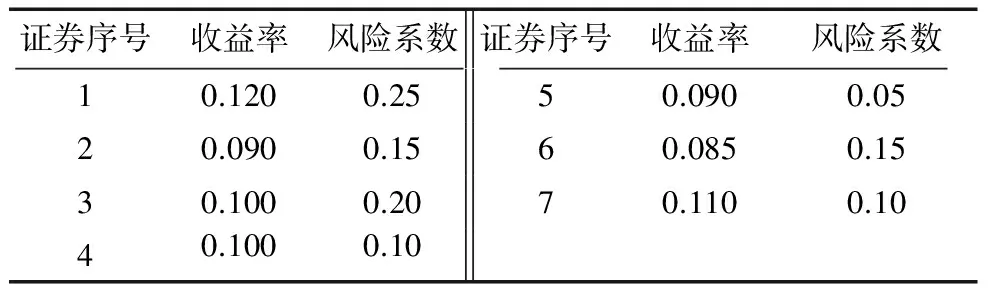
表1 7种证券的期望收益和风险系数 %

由表1可以看出,7种证券的平均期望收益率R≥0.10,风险系数β≤0.11,置信水平α≥0.9.在上述情况下,利用等价性算法进行模拟计算,得到的最优投资组合比例为:

x*=(0.151 7, 0.014 7, 0.071 4, 0.109 6,0.446 7, 0.018 2, 0.187 7)T.资产组合收益为0.100 024;资产组合风险为0.109 205.

从上述算例的结果可以看出,在个人期望收益率水平和风险水平满足一定要求的条件下,最优投资组合比例与所选取证券的收益率和证券本身的风险系数都有一定的关系,并且随着置信水平α的变化而呈现不同的最优投资组合比例.

4 结 语

本文借助于概率测度和置信水平,给出了组合证券投资决策的随机规划模型.针对风险证券投资组合收益率随机向量不服从正态分布的情况,给出了模型的等价性线性规划算法,并利用Matlab进行求解.数值算例结果表明该算法简便、可行、有效.

[1] TANG Wangsheng, XU Yanli,HAN Qiheng.Optimal control of a class of stochastic systems with probability criterion[J].Advance in Systems Science and Applications,2000,1(1):83-87.

[2] DENG Xiaotie,WANG Shouyang,XIA Yusen.Criteria,models and strategies in portfolio selection[J].Advanced Modeling and Optimization,2000,8(2):79-103.

[3] 韩其恒,唐万生,李光泉.机会约束下的投资组合问题[J].系统工程学报,2002,17(1):87-92.

[4] 傅荣林.组合证券投资的概率准则模型探讨[J].运筹与管理,2002,11(4):97-105.

[5] 唐万生,梁建峰,韩其恒.组合证券投资的概率准则模型[J].系统工程学报,2004,19(2):193-197.

[6] 王燕青,唐万生,韩其恒.基于遗传算法的概率准则组合证券模拟求解[J].管理科学学报,2002,5(6):29-33.

[7] 张莉,唐万生,宋军.概率准则下组合投资的整数规划模型[J].天津大学学报:社会科学版,2003,5(2):126-128.

[8] 徐金虹,徐维军,李引生.概率原则下基于投资者偏好的组合投资选择[J].系统工程学报,2005,20(5):544-548.

[9] 刘勇,马良.投资者偏好条件下概率准则投资组合问题求解[J].运筹与管理,2013,22(3):174-178.

[10] 王晓芳,翟永会,闫海峰.机会约束下风险最小的投资组合选择模型研究[J].统计与决策,2009(23):9-10.

(编辑 白林雪)

A Stochastic Model and Algorithm in Portfolio Selection

LIU Xiaojuan

(SchoolofMathematicsandPhysics,ShanghaiUniversityofElectricPower,Shanghai200090,China)

A stochastic model is given for portfolio selection by the probability measure and confidence level.The difference solutions are obtained based on random variable distributing,namely,the conventional optimization algorithm and the equivalent linear programming algorithm.The experiment results show that the proposed algorithm is simple and feasible,and has practical value.

securities investment choice; stochastic model; probability measure; linear programming

10.3969/j.issn.1006-4729.2017.03.018

2015-08-24

刘晓娟(1977-),女,博士,讲师,山东高密人.主要研究方向为最优化理论,最优预测及控制等.E-mail:xiaojl_01@163.com.

F830.9

A

1006-4729(2017)03-0304-03