基于改进粒子群算法的DG功率因数优化模型研究

施泉生, 陆亚南, 张圣富

(1.上海电力学院, 上海 200090; 2.国家电网泗阳具供电公司, 江苏 宿迁 223700;3.国网泰安供电公司, 山东 泰安 271000)



基于改进粒子群算法的DG功率因数优化模型研究

施泉生1, 陆亚南2, 张圣富3

(1.上海电力学院, 上海 200090; 2.国家电网泗阳具供电公司, 江苏 宿迁 223700;3.国网泰安供电公司, 山东 泰安 271000)

在配电网电源充裕的前提下,通过调节可控分布式电源的功率输出来优化配电网运行,稳定节点电压,降低线路损耗.结合PQ控制理论,通过调节分布式电源的功率因数来控制分布式电源有功功率和无功功率的输出.利用粒子群算法求解可控分布式电源的最优功率因数值,智能优化配电网运行.最后选取IEEE33节点配电系统进行算例分析,以验证该方法的有效性.

分布式电源; 配电网; 粒子群; 功率因数; 优化

根据分布式电源(Distributed Generation,DG)是否具有稳定的输出功率,可将其分为稳定性分布式电源(stable DG,SDG)和不稳定性分布式电源(non-stable DG,NSDG)两种.SDG包括小型燃气轮机、蓄电池等,NSDG包括光伏发电、风力发电等.根据输出功率是否可控,又可以分为可控式分布式电源(controllable DG,CDG)和不可控式分布式电源(non controllable DG)两种.随着分布式电源技术的发展,未来分布式电源在配电网中的比重将会越来越大.

分布式电源并入配电网,会对配电网的运行产生一定的影响.国内外学者对分布式电源并入配电网的影响进行了大量的研究.文献[1]研究了DG接入配电网后对设备运行成本的影响,通过调节DG的无功输出,以控制配电网设备的运行成本;文献[2]研究了DG对配电网自动化系统故障定位的影响,提出了改进故障定位策略,以解决含分布式电源架空配电网故障定位的难题;文献[3]和文献[4]主要研究了DG的接入位置和接入容量对配电网经济性的影响,并采用遗传算法产生各种选址和定容方案;文献[5]主要分析了DG的接入位置和接入容量对配电网电压、电流的影响,并以谐波畸变为约束条件;文献[6]主要研究了天气对分布式电源并网容量的影响,综合考虑了负荷的年运行费用问题;文献[7]研究了多目标函数的优化模型,并用遗传算法确定了DG的最优接入位置和并网容量.

对于分布式电源并网的研究,主要集中在两方面:一是改善配电网设备,使其适应分布式电源并网的影响[1-2];二是优化DG的接入位置和接入容量,将其对配电网的不利影响降至最低[3-7].本文提出通过调节稳定的可调控的分布式电源(Stable controllable DG,SCDG)的功率因数来优化配电网运行的策略,通过控制SCDG的功率因数,调节SCDG有功功率和无功功率的输出,然后利用粒子群算法对每个方案进行更新、调节,通过前推回代算法对每个方案进行潮流计算,求得每个方案的节点电压和网损,再通过不断更新、比较,最终找到全局最优解.

1 分布式电源功率因数优化模型

分布式电源的并网运行会影响配电网的潮流走向.控制分布式电源有功功率和无功功率的输出,可以调节配电网的潮流分布.有功功率与无功功率满足关系:

(1)

式中:P——有功功率;Q——无功功率;φ——功率因数角.

因此,可以通过调节DG的功率因数cosφ来调节DG的有功功率和无功功率.在配电网并网运行时,大电网可以为配电网提供充足的有功功率,故可以通过调节DG的功率因数来控制DG的功率输出,优化配电网运行.基于上述分析结果,提出分布式电源功率因数优化模型,通过调节分布式电源的功率因数,控制分布式电源有功功率和无功功率的输出,以调节配电网的潮流,使得配电网的网损最小.文献[3]指出DG的接入位置和接入容量都对配电网系统有影响,所以每个DG的接入位置和接入容量都是事先规划好的.

1.1 目标函数

分布式电源并网运行,会对配电网产生很多影响,包括改变配电网的潮流分布,影响保护装置的整定值等.本文主要研究分布式电源并网运行对配电网潮流的影响.选取配电网网损最小为目标函数,即:

(2)

式中:Ploss——配电网有功网损;N——配电系统的总支路数;Ri——第i条支路的电阻;Pi,Qi——第i条支路上的有功、无功功率;

Ui——第i条支路的母线电压.

1.2 约束条件

配电网稳定运行必须满足潮流约束、电压约束、容量约束等.

1.2.1 潮流约束

配电网的各节点必须满足有功功率、无功功率的平衡,即:

Pi+PDGi=PDi+

(3)

Qi+QDGi=QDi+

(4)

式中:Nb——节点总个数;Pi,Qi——节点i注入的有功功率和无功功率;

PDGi,QDGi——DG向节点i注入的有功功率和无功功率;

PDi,QDi——节点i所带负荷;

Ui,Uj——节点i和j的节点电压;

Gij,Bij,δij——节点i和j之间的电导、电纳和电压相角差.

1.2.2 电压约束

为了保证配电网的供电质量,配电网各节点的电压必须限定在一定范围内,电压约束条件如下:

(5)

式中:Ui,max,Ui,min——表示节点i的电压上下限.

《配电网规划设计技术导则》Q/GDW 1738—2012规定,10 kV及以下三相电压允许偏差为额定电压的±7%,即Ui,min=额定电压×(1-7%),Ui,max=额定电压×(1+7%).

1.2.3 DG的容量约束

DG的接入容量和接入位置会对配电网产生影响,因此DG的发电容量不能超过其上限.

(6)

式中:PDGk,QDGk——第k个DG发出的有功功率和无功功率;

SDGk——第k个DG的额定容量.

1.2.4 线路功率约束

为了防止线路重载、过载,每条线路都会设定其功率上限,即:

(7)

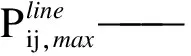
2 改进的粒子群算法

粒子群优化算法(Particle Swarm Optimizer,PSO)是一种智能优化算法[8],可以通过不断更新种群中粒子的位置和速度信息,搜索全局最优解.设粒子群为d维空间,则第i个粒子的位置、速度可以分别表示为Xi=[xi1,xi2,xi3,…,xid],Vi=[vi1,vi2,vi3,…,vid].Pbest表示每个粒子的历史最优位置,记作[pi1,pi2,pi3,…,pid];gbest表示全局历史最优位置,记作[pg1,pg2,pg3,…,pgd].

基本公式定义如下:

(8)

(9)

式中:c1,c2——学习因子,通常c1=c2=2.0;r1,r2——[0,1]之间的随机数;w——惯性权重,一般在0.4到0.9之间取值.

文献[9]指出,随着迭代次数的增加,w线性减少,将会大大改善算法的收敛性.其基本公式为:

w=wmax+

(10)

式中:wmax,wmin——最大和最小惯性系数;k,K——当前迭代系数和总迭代次数.

3 基于改进粒子群算法的功率因数优化模型

3.1 粒子位置信息说明

粒子群算法中,每个粒子的位置信息都表示一种方案,本文每个粒子的位置信息表示配电网中每个分布式电源的功率因数值.假设配电网中存在n个可控DG,第i个可控DG的功率因数记作cosφi(i=1,2,3,…,n),那么粒子群中,第i个粒子的位置信息可以记作Xi=[cosφ1,cosφ2,cosφ3,…,cosφn].利用式(8)和式(9)不断更新粒子的位置和速度信息,直至求得最优解或者到达迭代次数为止.

3.2 罚函数优化分布式电源功率因数优化模型

罚函数法主要是利用辅助函数将有约束问题转换为无约束问题,可分为内点法和外点法两种.

分布式电源功率因数优化模型存在约束问题,利用惩罚函数可将有约束问题转换成无约束问题.

约束条件主要有潮流约束、电压约束 、容量约束、线路功率约束等,其中潮流约束可以通过潮流计算自动满足.本文假设配电网中的分布式电源都满容量运行,因此容量约束也自动满足,故仅剩下电压约束和线路功率约束两个约束条件.利用外点法将目标函数、电压约束、线路功率约束写成扩展目标函数,即:

(11)

式中:f(x)——目标函数;U1,U2——电压约束和线路功率约束;λ1,λ2——罚因子.

3.3 算法流程

本文建立了基于改进粒子群算法的分布式电源功率因数优化模型.利用文献[9]的思想将粒子群算法中的惯性权重线性进行变换,以提高粒子群的搜索精度.将分布式电源的功率因数作为种群中粒子的位置信息,用前推回代算法进行潮流计算[10-11],并通过式(11)求得适应度值;然后利用式(8)和式(9)更新粒子的位置信息和速度信息,再进行不断迭代直至找到最优解或者迭代结束为止.具体步骤如下.

(1) 初始化各参数,包括粒子数N,粒子维数D,迭代次数K,惯性权重w1和w2,学习因子c1和c2.

(2) 随机生成N个初始粒子.

(3) 计算各个粒子的适应度值.对种群中每个粒子,利用前推回代算法进行潮流计算,求得各个方案的适应度值.将目前的粒子位置作为个体的历史最优解p_best,适应度值为p_best_fit,并将该种群中最好的位置作为全局最优解g_best,全局最优适应度值为g_best_fit.

(4) 采用式(8)和式(9)更新粒子的速度和位置.

(5) 计算新粒子的适应度值fitness.将新粒子中的每个方案通过前推回代算法进行潮流计算,并求得其适应度值fitness.比较fitness,p_best_fit,如果fitness>p_best_fit,则将fitness赋给p_best_fit,同时更新p_best.否则直接进行下一步.

(6) 由新的p_best_fit,p_best,更新g_best_fit,g_best.

(7) 判断K,若k>K,则输出最优解;否则转至步骤(4).

4 算例分析

本文针对IEEE33节点配电系统做算例分析.IEEE33节点配电系统的参数见文献[12].并在IEEE33节点配电系统的7,23,29节点并入3个可控的分布式电源,如图1所示.假设3个SCDG都满容量运行,且3个SCDG的额定容量均为1 000 kW.

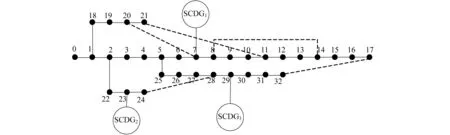
图1 包含DG的IEEE33节点配电系统

参数设置如下:粒子维度D=3;粒子种群N=20;最大迭代次数K=100;惯性权重系数起始值wstar=0.4,最终值wend=0.9;粒子的速度取值范围为v=[-0.15,0.15];粒子的加速系数c1=c2=2;罚函数中罚因子λ1=λ2=999;系统电压基准值UB=12.66 kV,功率基准值SB=1 000 kW.

为了验证分布式电源功率因数优化模型的优越性,本文分别在4种情况下分析了配电网网损情况以及配电系统中各节点电压情况.4种情况分别为配电网中不存在DG;配电网中全部DG都发出无功功率,不发出有功功率;配电网中全部DG都发出有功功率,不发出无功功率;利用分布式电源功率因数优化模型.4种情况下配电网网损情况如表1所示,配电网中各节点电压情况如图2所示.

由表1可以发现,利用分布式电源功率因数优化模型后,配电网网损值最小,配电网全额发出有功功率次之,而配电网未加入分布式电源时,配电网网损值最大,说明分布式电源并网运行对配电网降低网损具有重要意义.

此外,分布式电源全额发出有功功率对配电网网损值的影响优于分布式电源全额发出无功功率.与另外3种情况相比,利用分布式功率因数优化模型可以将网损值分别降低80.24%,72.01%,53.81%.由此可见,利用分布式功率因数优化模型对配电网优化运行具有重要意义.

表1 优化前后配电网系统总网损比较

图2 4种情况下节点电压的分布曲线

由图2可以发现,分布式电源在没有并网之前,配电网末端节点电压降低严重,在10～17节点、28～32节点的电压降低已超过额定电压的7%;分布式电源并网后配电网各节点电压明显提高,其中分布式电源全额发出有功功率的节点电压提高情况优于分布式电源全额发出无功功率.利用分布式电源功率因数优化模型以后,配电网各节点电压都保持在0.96 (p.u)以内,节点电压质量从优,且4种情况下其节点电压为最高值.

5 结 论

(1) 分布式电源并网运行后,配电网原来线路的单向潮流会发生变化,使得系统总网损得到有效降低;

(2) 对于并网运行的分布式电源,全额发出有功功率比全额发出无功功率更有利于降低配电网网损;

(3) 对并网的分布式电源进行功率因数优化,可以大幅降低配电网的网损;

(4) 分布式电源功率因数优化有助于提高配电网各节点的电压,保障配电网的电压质量.

[1] 陈树恒,党晓强,李兴源,等.考虑DG接入与设备运行成本的配电网无功优化[J].电力系统保护与控制,2012(21):36-41.

[2] 刘健,张小庆,同向前,等.含分布式电源配电网的故障定位[J].电力系统自动化,2013(2):36-42.

[3] 王成山,陈恺,谢莹华,等.配电网扩展规划中分布式电源的选址和定容[J].电力系统自动,2006,30(3):38-43.

[4] ASANO H,WATANABE H,BANDO S.Methodology to design the capacity of micro grid[C].IEEE International Conference on System of Systems Engineering,2007:1-6.

[5] 江南,龚建荣,甘德强.考虑谐波影响的分布式电源准入功率计算[J].电力系统自动化,2007,31(3):19-23.

[6] 郑漳华,艾芊,顾承红,等.考虑环境因素的分布式发电多目标优化配置[J].中国电机工程报,2009,29(13):23-28.

[7] CELLI G,GHIANI E,MOEEI S,etal.A multi-objective formulation for the optimal sizing and siting of generation in distribution networks[C].Power Tech.Conference Proceedings,IEEE Bologna,2003:67-74.

[8] KENNEDY J,EBERHART R C.Particle swarm optimization[C]//Proceedings of IEEE Conference on Neural Networks,Perth,Australia,1995:1 942-1 948.

[9] SHI Y H,EBERHART R C.A modified particle swarm optimizer[C]//Proc. IEEE Int Conf. on Evolutionary Computation,Anchorage,USA,1998:69-73.

[10] 王守相,王成山.现代配电系统分析[M].北京:北京高等教育出版社,2007:58-64.

[11] 张立梅,唐巍.计及分布式电源的配电网前推回代潮流计算[J].电工技术学报,2010(8):123-130.

[12] BARAN M E,WU F F.Network reconfiguration in distribution systems for loss reduction and load balancing[J].IEEE Transactions on Power Delivery,1989(2):1 401-1 407.

(编辑 胡小萍)

Research on Power Factor Optimization Model of DG Based on Improved Particle Swarm Algorithm

SHI Quansheng1, LU Yanan2, ZHANG Shengfu3

(1.SchoolofEconomicsandManagement,ShanghaiUniversityofElectricPower,Shanghai200090,China; 2.StateGridSiyangCountyPowerSupplyCompany,Suqian223700,China; 3.StateGridTai’anPowerSupplyCompany,Tai’an271000,China)

In the condition of sufficient distribution network power operation of the distribution network is optimized by adjusting the power output of the controllable distributed generation,including stabling node voltage and reducing line losses.By adopting PQ control theory,the active and reactive power output of distributed generation can be controlled by adjusting the power factor of distributed generation.The optimal power factor of distributed generation is searched by particle swarm algorithm.Finally,the effectiveness is verified by the simulation results of IEEE 33-bus system with DGs.

distributed generation; distribution net work; particle swarm; power factor; optimization

10.3969/j.issn.1006-4729.2017.03.002

2016-03-02

陆亚南(1991-)，男，硕士，江苏沭阳人.主要研究方向为配电网规划,电力经济等.E-mail:1035 021464@qq.com.

上海高校人文社会科学重点研究基地“一带一路”能源电力管理与发展战略研究中心项目(WKJD15004).

TM715;TM73

A

1006-4729(2017)03-0216-05