考虑供电可靠性的智能配电网优化重构

屠亦军, 廖剑波, 王泽安

(1.国网浙江省电力公司舟山供电公司, 浙江 舟山 316000; 2.国网福建省电力有限公司福州供电公司, 福建 福州 350009; 3.美国洛杉矶钻石吧高中, 美国 洛杉矶 90001)



考虑供电可靠性的智能配电网优化重构

屠亦军1, 廖剑波2, 王泽安3

(1.国网浙江省电力公司舟山供电公司, 浙江 舟山 316000; 2.国网福建省电力有限公司福州供电公司, 福建 福州 350009; 3.美国洛杉矶钻石吧高中, 美国 洛杉矶 90001)

配电网馈线联络的不断加强和配电自动化的建设使网络重构成为可能,通过对网络开关的调度控制来优化调整配电网的网络结构,从而提高配电网的供电可靠性.在传统经济性重构的基础上,进一步考虑了供电可靠性,提出了一种计及网损和系统停电损失的智能配电网优化重构模型,并采用改进遗传算法对IEEE 33节点配电系统进行优化重构问题的求解,结果表明,所提模型和算法具有可行性.

配电网重构; 网损; 可靠性; 改进遗传算法

随着技术和经济的发展,社会对供电的质量、连续性和可靠性的要求越来越高.供电可靠性关系到人民群众的生活和社会的安定.欧美等发达国家非常重视提升供电可靠性,其供电可靠性水平均较高.譬如:美国各电力公司供电可靠性基本上达到了一个稳定的趋势,中心城区供电可用率指标基本上能够达到99.99%;日本东京电力公司1986年之后的供电可靠率都在99.99%以上;新加坡供电可靠率更是达到99.999 7%,用户平均停电时间仅1.57 min;英国国家电网公司的可靠性指标在99.999 7%以上.相比之下,我国供电可靠性虽进步很快,相较国际先进城市差距仍较大,上海核心城区供电可靠性距离A+区域定位仍明显不足.

配电网是电力系统电能分配的末端环节,优化配电网的运行状态对系统降损、供电可靠性和电能质量的提高具有重要意义.目前各地普遍采用增加馈线联络和建设配电自动化等手段,来提高配电网的供电可靠性[1].正常运行条件下,配电网通过降压变电站向一个树状网络的供电区域供电,单个供电段之间通过一个常合的开关相接,而不同的供电区域之间则由常开开关联系.随着联络开关的增加,在配电自动化系统的辅助下对网络开关进行调度控制,可实现网络结构的优化调整,从而进一步提高供电可靠性.配电网的网络拓扑结构是影响电网可靠性、网损、供电电压质量、设备负载水平的关键,研究配电网优化重构方法对提高配电网各项技术经济指标具有重要意义.

近年来,许多专家学者对配电网优化重构进行了研究.文献[2]定义了配电网的最大供电能力指标,以开关动作次数最少和供电能力最大为目标建立了配电网的优化重构模型,并采用二进制粒子群算法进行模型求解.文献[3]综合考虑了网损、电压偏差和馈线负荷平衡,基于模糊隶属度函数建立了优化重构的多目标模型.文献[4]主要计及了网损的经济性目标,以改进和声搜索算法为求解工具,研究了配电网的优化重构问题.文献[5]在重构中考虑了网损成本、开关动作成本等经济因素,提出了一种配电网优化重构方法.目前配电网优化重构的研究主要关注网络运行的经济性,缺乏对配电网供电可靠性等因素的考虑,而网络结构能够显著影响配电网的供电可靠性,在重构研究中应当予以考虑.

本文在计及传统经济性目标的基础上,考虑系统供电可靠性对网络重构的影响,探索更为全面有效的配电网优化重构方法.

1 配电网优化重构的数学模型

配电网的优化重构就是在所有可能的网络结构中,找出一套既能满足网络运行约束(辐射状网络拓扑、电压极限、线路载流极限等),又能最大化某种价值目标的结构方案,在满足负荷用电需求的基础上,促进网络的经济安全运行.

1.1 目标函数

本文提出了一种配电网的优化重构模型,采用网络损耗最小作为重构的经济性目标,以系统停电损失最小为重构的可靠性目标,综合考虑经济性与可靠性,构建优化重构目标函数如下:

(1)

(2)

(3)

式中:α1——经济性目标的权重系统;α2——可靠性目标的权重系数;S——年最大损耗小时数;D——平均电价;Ploss——网络损耗;N——网络节点数;ENSi——负荷i的电量不足期望值;CICi——负荷i的停电损失电价;kij——节点i至节点j的支路(支路i-j)的开关状态,取值1为开关闭合,取值0为开关打开;

Rij——支路i-j的电阻;

Pij——支路i-j的有功功率;

Qij——支路i-j的无功功率;

Uj——节点j的电压幅值;

wi(K)——状态K下负荷i的连接负荷;

K——网络中所有开关的状态;

λi——负荷i的故障率;

ri——负荷i单次故障的平均停电时间.

基于该目标来实施配电网的优化重构,既计及了对网络损耗的优化,又考虑了网络结构对系统供电可靠性的影响,综合协调了重构的经济性与可靠性.

1.2 约束条件

在配电网的优化重构工作中,还应该考虑多种约束条件.最小允许可靠性约束为:

(4)

节点电压上下限约束为:

(5)

线路载流量约束为:

(6)

网络潮流约束为:

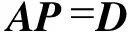
(7)

配电网拓扑辐射结构约束为:

(8)

式中:R——某种决策方案下的可靠性指标; Rmin——可靠性指标允许的最小值; U——节点电压; Umax,Umin——节点电压的上下限; I——支路电流; Imax——支路电流上限; A——节点支路关联矩阵; P——馈线潮流向量; D——负荷向量; o——某种决策方案下配电网的网络结构; Orad——配电网辐射状网络结构集合.

2 基于改进遗传算法的重构模型求解策略

配电网优化重构是一个组合优化问题,具有离散性、非线性和高维性等特点[6].遗传算法(Genetic Algorithm,GA)具有原理简单、编码简洁、搜索能力强、适用性好等优点,被广泛应用于配电网各类优化问题的求解[7-9].

在配电网优化重构问题的求解中,遗传算法的染色体采用离散的0-1编码,根据开关的开合或线路被选择与否来确定0-1取值.由于配电网的支路和环数一般较多,若仅依靠传统遗传操作进行寻优,算法迭代可能产生大量的不可行解,存在收敛速度慢、局部精确寻优能力弱等不足.因此,本文对遗传算法进行了改进:一方面,在算法的选择操作中采用了精英保留策略,在遗传操作施行前,将当前种群的精英个体保留,不参与遗传操作,如此避免了优秀个体遗传信息的丢失,保证了遗传操作所产生个体的优良性,明确了搜索方向,且加快了种群进化速度;另一方面,在交叉和变异的操作中,引入了自适应的概率参数,具体算式为:

(9)

(10)

式中:pc——交叉概率;pc,max,pc,min——最大和最小交叉概率;it——当前迭代次数;it,max——最大迭代次数;pm——变异概率;pm,max,pm,min——最大和最小的变异概率;f′——两个交叉个体中较大的适应度值;f——要变异个体的适应度值;favg——种群平均适应度值.

以上改进的遗传算法既保证了全局搜索能力,又增强了局部搜索能力,有效减少了迭代次数,提高了算法的收敛性能.基于改进遗传算法的配电网优化重构求解策略流程如图1所示.

图1 基于改进遗传算法的配电网优化

3 仿真与分析

对IEEE 33节点配电系统[10]进行优化重构研究,系统网络结构如图2所示.系统额定电压为12.66 kV,总有功负荷为3 715 kW,无功负荷为2 300 kW.初始状态下,5条支路装有联络开关,分别为支路7-20,11-21,8-14,17-32,24-28,其余支路均装有分段开关.设定年最大负荷损耗时间为3 200 h,年平均电价取0.6元/kWh,停电损失电价折算倍数取为25.遗传算法种群大小为50,最大进化代数为100,采用改进遗传算法对该算例进行计算.

图2 IEEE 33节点配电系统网络结构

分别针对几种典型模型进行计算:

(1) 初始模型(优化重构前);

(2) 模型1,即经济性模型,α1=1,α2=0,此模型意在寻找网损最低的拓扑结构;

(3) 模型2,即可靠性模型,α1=0,α2=1,此模型意在寻找可靠性最高,即电量不足期望值最小的拓扑结构;

(4) 模型3,即综合模型,α1=0.5,α2=0.5,此模型综合考虑经济性和可靠性指标.

表1为不同模型的重构效果比较.

表1 不同模型的重构效果比较

由表1可以看出,初始状态的拓扑结构网络损耗为211.296 kW,电量不足期望值为24 397.421 kWh;对于寻找网损最小的模型1来说,最低网损为140.413 kW;模型2找到了可靠性最高的拓扑结构,其电量不足期望值为18 926.485 kWh;综合考虑经济性和可靠性的模型3给出了本文目标函数最优的结构,即分别打开支路6-7,8-9,13-14,31-32,24-28联络开关.3种模型中,模型1的综合费用最少,约为26.6万元,模型2的综合费用约为28.4万元,但是这两种模型没有同时兼顾可靠性和网损最小的问题,模型3的综合费用约为28万元,比模型1多出1.4万元,但是却进一步提高了可靠性,并较大程度降低了网损.

图3给出了对模型3采用本文算法优化前后系统各节点电压变化.由图3可以看出:优化前,节点17电压水平最低,为0.939 143 p.u.;优化后,节点31电压最低,为0.962 455 p.u..

图3 开关状态优化前后系统电压变化

图4,图5,图6给出了对模型3分别采用改进遗传算法和普通遗传算法寻优的收敛过程.通过对比可以看出:随着优化的进行,两种方法搜到的网损均逐步下降,可靠性也逐步提高;本文算法首次搜到最优解的代数为16代,进行到35代时,迭代结果逐步收敛,而简单遗传算法需要首次搜到最优解的代数为31代,进行至68代左右才能收敛.由此可见,本文算法在对简单遗传算法的改进方面效果较为显著.

图4 网络损耗随遗传代数的变化

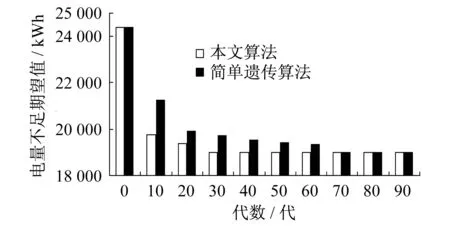
图5 电量不足期望值随遗传代数的变化

图6 综合目标值随遗传代数的变化

4 结 语

本文提出了一种考虑供电可靠性的智能配电网优化重构方法,构建了网损和系统停电损失最

小的综合优化模型.从精英保留、交叉与变异概率算子自适应两个方面,对遗传算法进行了有效的改进,提高了算法计算效率和收敛性.应用改进遗传算法对IEEE 33节点配电系统进行优化重构问题的求解,算例分析说明该方法能够有效降低配电网网损,改善电压质量,提高供电可靠性;所提出的改进遗传算法较传统算法具有更好的收敛性.

[1] 王守相,王成山.现代配电系统分析[M].北京:高等教育出版社,2007:115-116.

[2] 靳小龙,穆云飞,贾宏杰,等.面向最大供电能力提升的配电网主动重构策略[J].电工技术学报,2014,29(12):137-147.

[3] SYAHPUTRA R,ROBANDI I,ASHARI M.Optimal distribution network reconfiguration with penetration of distributed energy resources[C]// 2014 1st International Conference on Information Technology,Computer and Electrical Engineering.Portland,USA:IEEE,2014:388-393.

[4] SUDHA D,SUBRAHMANYAM N,SYDULU M.Self adaptive harmony search algorithm for optimal network reconfiguration[C]// 2014 Power and Energy Conference.USA:IEEE,2014:1-6.

[5] 巩晓昕,舒彬,吴振升.主动配电网动态重构方法研究[J].电气技术,2014(12):52-60.

[6] 赵立儒.基于智能算法的主动配电网自愈及调度优化研究[D].秦皇岛:燕山大学,2015.

[7] 黄红程,顾洁,方陈.基于无向生成树的并行遗传算法在配电网重构中的应用[J].电力系统自动化,2015,39(14):89-96.

[8] 冯雪平,宋晓辉,梁英,等.基于最小生成树及改进遗传算法的含分布式电源配电网孤岛划分方法[J].高电压技术,2015,41(10):3 470-3 478.

[9] 刘健,李京航,柏小丽.基于精英保留策略遗传算法的配电网无功优化[J].电气技术,2015(4):35-38.

[10] COVANLAR S,GRAINGER J,YIN I,etal.Distribution feeder reconfiguration for loss reduction[J].IEEE Trans on Power Delivery,1988,13(3):1 217-1 223.

(编辑 桂金星)

Optimal Reconfiguration of Intelligent Distribution Network Considering Power Supply Reliability

TU Yijun1, LIAO Jianbo2, WANG Zean3

(1.ZhoushanPowerSupplyCompany,StateGridZhejiangElectricPowerCompany,Zhoushan316000,China; 2.FuzhouPowerSupplyCompany,StateGridFujianElectricPowerCompany,Fuzhou350009,China; 3.LosAngelesDiamondBarHighSchool,LosAngeles90001,USA)

The strengthening of tie switch and the construction of distribution automation make reconfiguration of distribution network possible.By scheduling the switches,the network structure of distribution network can be optimally adjusted,and the power supply reliability of distribution network is improved.Based on the traditional economic reconfiguration,the reliability of power supply is further analyzed.An optimal reconfiguration model of intelligent distribution network considering grid loss and system power loss is proposed.The improved genetic algorithm is applied to achieve optimal reconfiguration results of IEEE 33 bus system,which shows the feasibility of the proposed model and algorithm.

distribution network reconfiguration; grid loss; reliability; improved genetic algorithm

10.3969/j.issn.1006-4729.2017.03.006

2017-03-31

廖剑波(1991-),男,硕士,福建三明人.主要研究方向为主动配电网优化调度运行等.E-mail:liaojianbox@163.com.

国家自然科学基金(51407113).

TM711

A

1006-4729(2017)03-0239-05