X12CrMoWVNbN10-1-1钢高温裂纹扩展特性分析

吴臻茂, 纪冬梅, 张亚杰,2, 朱月梅

(1.上海电力学院, 上海 200090; 2.中电国际姚孟第二发电有限公司, 河南 平顶山 467031;3.上海电气电站设备有限公司 上海汽轮机厂, 上海 200240)



X12CrMoWVNbN10-1-1钢高温裂纹扩展特性分析

吴臻茂1, 纪冬梅1, 张亚杰1,2, 朱月梅3

(1.上海电力学院, 上海 200090; 2.中电国际姚孟第二发电有限公司, 河南 平顶山 467031;3.上海电气电站设备有限公司 上海汽轮机厂, 上海 200240)

裂纹的萌生是汽轮机转子不可避免的问题,而裂纹的扩展对电厂运行产生极大的威胁.X12CrMoWVNbN10-1-1钢在火电领域应用广泛,针对X12CrMoWVNbN10-1-1转子钢高温下的裂纹扩展特性进行了分析:对X12CrMoWVNbN10-1-1钢在620 ℃下进行了疲劳裂纹扩展试验,对载荷、应力比及频率等参数影响裂纹扩展的情况进行了研究,并结合Paris模型、Forman模型以及C*参数模型,研究了X12CrMoWVNbN10-1-1钢高温疲劳及蠕变-疲劳交互作用下的裂纹扩展速率模型.结果表明,X12CrMoWVNbN10-1-1钢高温疲劳裂纹扩展速率da/dN与载荷水平P及频率f呈正相关,与应力比R呈负相关;Paris公式和Forman公式适合描述X12CrMoWVNbN10-1-1钢高温疲劳裂纹扩展速率,C*参数适合描述其蠕变-疲劳裂纹扩展速率.

X12CrMoWVNbN10-1-1钢; 高温疲劳; 蠕变-疲劳; 裂纹扩展

发电机组在调峰运行中频繁启停,使得汽轮机发生故障的机会增多,其灾难性事故时有发生.在美国,1950～1980年报道的汽轮机转子飞裂事故达到20起之多,其中美国加拉丁(Callatin)电厂2#机组转子破坏就是因为裂纹扩展导致失效的典型案例[1].大型汽轮机转子作为整锻或焊接件,在加工制造过程中难免会出现缺陷,在运行过程中也可能萌生裂纹.从断裂力学角度说,裂纹萌生并不意味着构件使用寿命的终止,只有当裂纹扩展到临界尺寸时才会失稳扩展,导致寿命终止.裂纹从萌生到扩展再到临界尺寸,通常需要经历很长的运行时间,因此如何保证构件的安全可靠运行,又能充分地利用其使用寿命,是工程上亟待解决的问题[2].陈龙[3]利用LCF-FCGM理论解析模型对Cr2Ni2MoV和X12CrMoWVNbN10-1-1等7种材料的疲劳裂纹扩展行为进行了预测.卫东[4]编写了国内蠕变-疲劳载荷交互作用下裂纹扩展试验方法,并在600 ℃下对X12CrMoWVNbN10-1-1进行了裂纹扩展试验.目前,国外尚缺少对X12CrMoWVNbN10-1-1钢的相关实验研究.

鉴于整个社会节能减排的呼声越来越高,提高发电机组蒸汽参数已成为趋势,超超临界发电技术在过去20多年内得到了广泛应用[5-7],由于9%～12%Cr马氏体耐热钢具有良好的力学性能,因此其逐渐成为超超临界机组用钢,如X12CrMoWVNbN10-1-1钢主要用于超超临界汽轮机转子,通常工作温度为600～650 ℃[8-10].为了获取X12CrMoWVNbN10-1-1钢在高温条件下的疲劳裂纹扩展特性,本文在620 ℃空气环境下对其进行应力控制的疲劳裂纹扩展试验,并分析了其在蠕变-疲劳交互作用下的裂纹扩展特性.

1 高温疲劳裂纹扩展试验

1.1 试验材料

试验材料选用X12CrMoWVNbN10-1-1高铬合金钢,该材料由德国研制开发,是一种改良型的12%Cr钢,主要用于超超临界汽轮机转子、叶片、气缸等部位.研究表明,其具有较好的综合力学性能、焊接性能和工艺性能,而且具有较高的高温持久强度和高温抗腐蚀性能.材料为低碳调质钢,经过淬火和高温回火的调质处理后,组织主要为回火马氏体(Tempered martensite),其化学成分如表1所示.

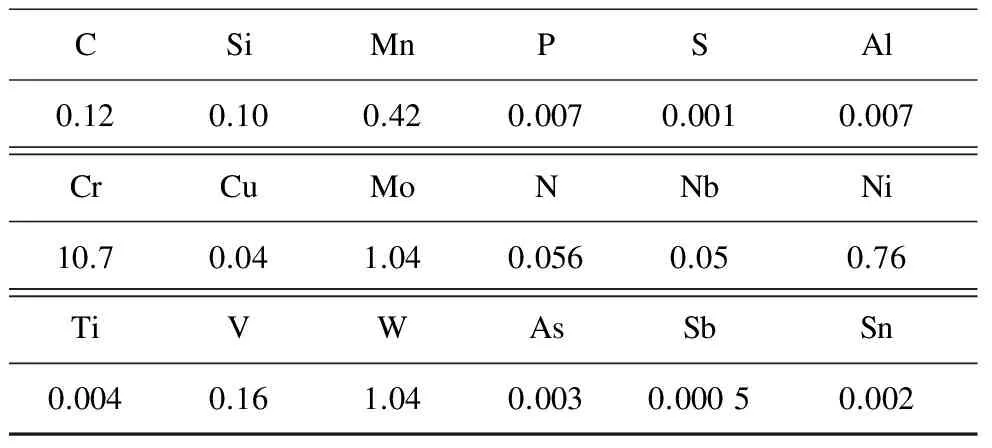
表1 X12CrMoWVNbN10-1-1的化学成分 %

1.2 试 样

试验按照ASTM E1457-00标准及GB/T6398—2000标准,并结合MTS370.10电液压伺服试验机实际情况,制成紧凑拉伸(CT)试样,如图1所示,图中单位均为mm.

试验前所有试样在试验机上以f=11 Hz,R=0.05预制1 mm的疲劳裂纹;应力强度因子范围ΔK计算公式[11]为:

(1)

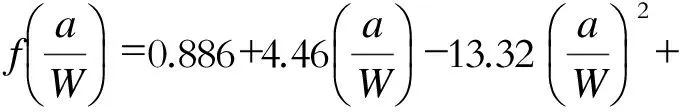
(2)

式中:ΔK——应力强度因子范围;a——裂纹长度;f——加载频率; ΔP——试验所用最大载荷与最小载荷之差;

W——加载线所在平面与基准面之间的宽度;

BN——厚度.

裂纹扩展速率采用七点递增多项式求得.

1.3 试验方法

试验在美特斯公司生产的MTS370.10电液压伺服多功能试验机上进行,标准紧凑拉伸试样与U型夹具之间采用销钉连接;试验温度为620 ℃,温度偏差不超过±3 ℃;环境为实验室大气.整个试验过程采用应力控制加载模式,试验装置如图2所示.加载波形如图3所示.

图2 试验装置

为了研究载荷水平、频率、应力比对疲劳裂纹扩展的影响,设置了不同的试验条件,最大载荷P分别为16 kN,18 kN,20 kN,35 kN;应力比R分别为0.1,0.3,0.5,0.7;频率f分别为0.5 Hz,1 Hz,3 Hz,5 Hz.裂纹扩展至9 mm时,卸掉载荷冷却至室温拉断.

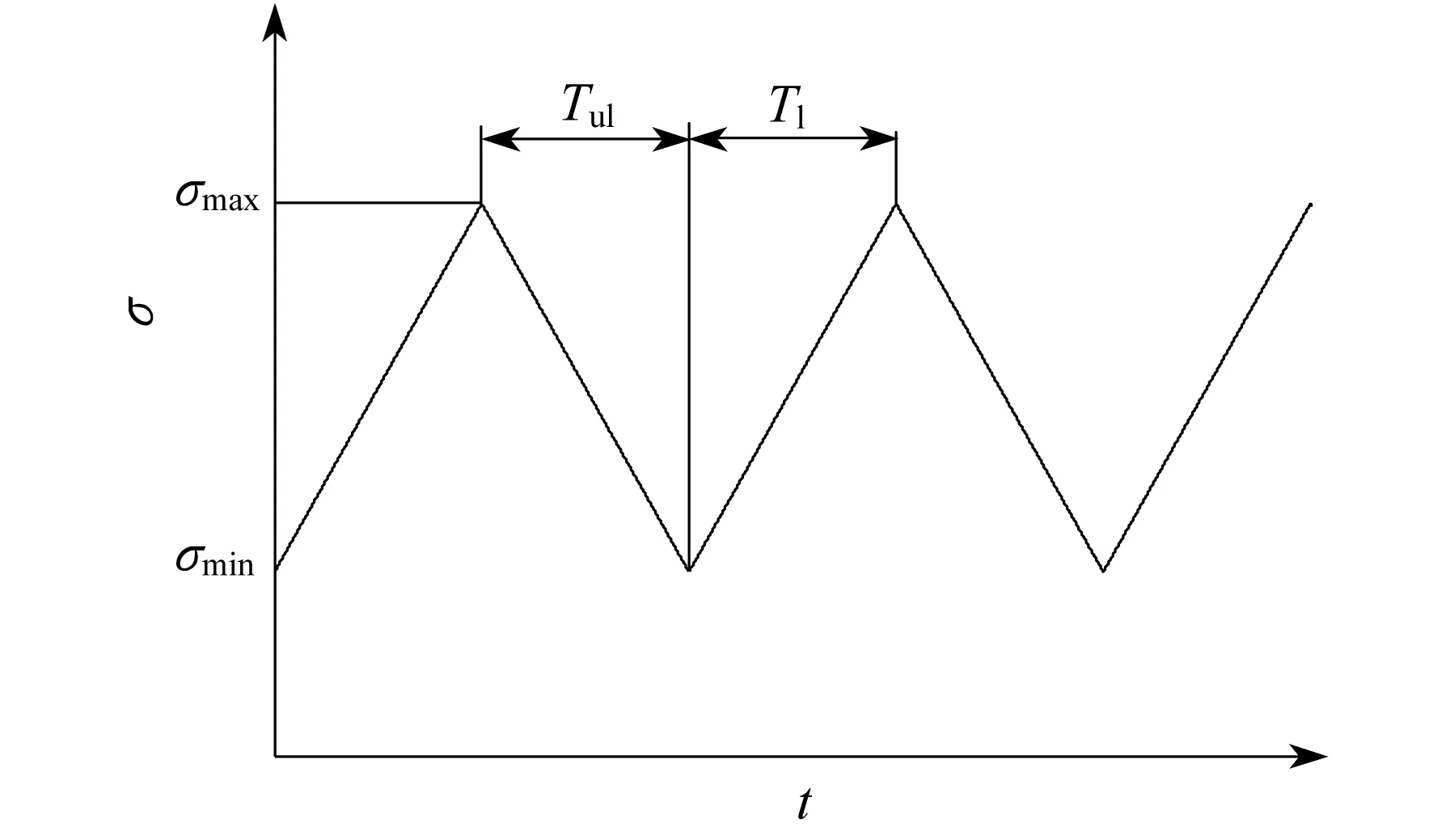
注:σmax—最大应力;σmin—最小应力;Tul—卸载时间;Tl—加载时间.

图3 疲劳裂纹扩展试验加载波形

2 试验结果

表2为X12CrMoWVNbN10-1-1钢620 ℃下疲劳裂纹扩展试验结果.从表2可以看出,失效时间最长为9.77 h,最短为1.02 h,该试验方案下疲劳裂纹快速扩展试验属于低周裂纹扩展.通过分析对比发现,应力比和加载频率相同时,载荷越大,失效时间越短,疲劳寿命越短;最大载荷和加载频率相同时,应力比越大,失效时间越长,疲劳寿命越长;最大载荷和应力比相同时,频率越大,失效时间越短,疲劳寿命先增大后减小,与频率不呈单调关系.随着应力比、频率的改变,失效时间发生了明显的变化,这两个疲劳因素对裂纹扩展影响比较显著.

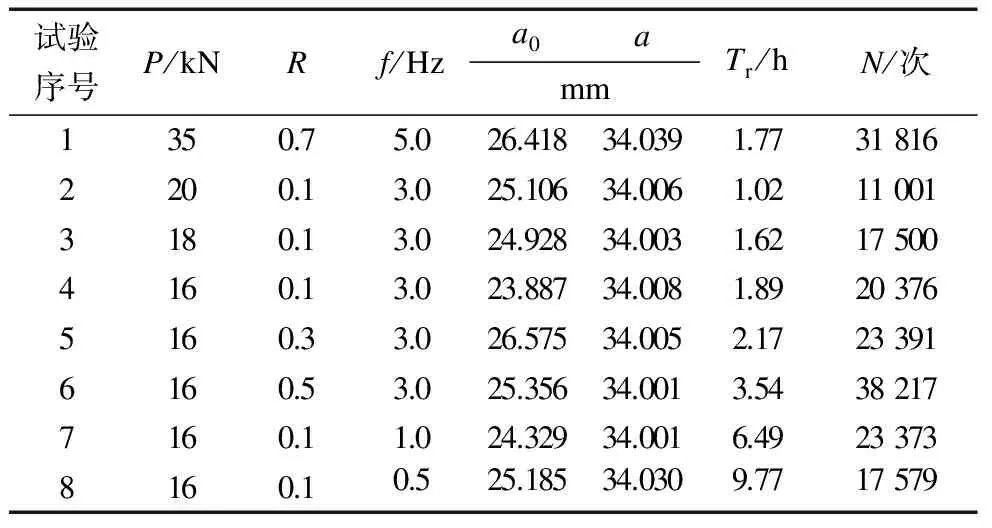
表2 X12CrMoWVNbN10-1-1钢620 ℃下疲劳裂纹扩展试验结果

注:a0—裂纹扩展初始长度;a—裂纹扩展长度;Tr—失效时间;N—循环寿命.

图4为各试验条件下裂纹长度随循环次数增长曲线.由图4可知,高温疲劳裂纹扩展曲线随着循环次数的增加呈“J”型.

图5为各试验条件下裂纹扩展速率曲线.由图5可知,高温疲劳裂纹扩展试验过程明显地呈现两个阶段:稳定扩展阶段和加速阶段,稳定扩展阶段裂纹扩展速率有不同程度的波动,但主体趋势呈缓慢增加;加速阶段裂纹扩展速率快速增大,波动变小,承力横截面的应力快速增大到达临界值,导致试样断裂.

图4 各试验条件下裂纹长度随循环次数增长曲线

图5 各试验条件下裂纹扩展速率曲线

3 X12CrMoWVNbN10-1-1钢裂纹扩展速率模型

3.1 高温疲劳裂纹扩展速率模型

迄今为止,国内外对疲劳裂纹扩展寿命预测的研究很多,其中建立应力强度因子和裂纹扩展速率之间关系的Paris 公式是目前工程中应用最为广泛的方法.Paris 公式是1963 年由Paris 和Erdogan 在实验基础上提出的疲劳裂纹扩展公式[12],它也是当今工程应用预测疲劳裂纹扩展寿命的理论基石,其公式为:

(3)

(4)

式中:da/dN——裂纹扩展速率,mm/次;a——裂纹长度,mm;N——应力循环次数;C,m——材料常数,环境因素如温度、湿度、介质、加载频率等都隐含在常数之中,可由实验数据拟合得到;

ΔK——应力强度因子范围;

f——一般为构件几何与裂纹尺寸的函数;

Kmax,Kmin——裂纹处应力强度因子的最大值和最小值;

Δσ——裂纹处应力幅值.

图6为不同试验条件下裂纹扩展速率与应力强度因子范围ΔK的关系曲线.图6中,直线为采用Paris公式对试验数据的拟合值.从图6可以看出,裂纹扩展速率da/dN与应力强度因子范围ΔK的双对数呈线性关系,实验值与拟合值比较吻合.另外,从图6还可以看出,载荷越大,裂纹扩展速率越快;应力比越大,裂纹扩展速率反而越小,并且随着应力比的增大,裂纹扩展的失稳阶段与稳定扩展阶段的差异性越来越小.而随着应力比的增大,平均应力在增大,根据载荷水平对裂纹扩展速率的影响,应力比的增大裂纹扩展速率也应该增大,表明应力幅值对裂纹扩展速率有较大的影响,即疲劳对高温裂纹扩展具有较显著的作用.试验4的裂纹扩展速率大于试验7小于试验8.随着频率的减小,裂纹扩展速率出现反复;裂纹扩展速率与载荷、频率呈正比,与应力比呈反比,频率改变能够显著影响裂纹扩展速率.

图6 在620 ℃时不同试验条件下裂纹扩展速率与应力强度因子范围ΔK的关系曲线

表3为各试验条件下裂纹扩展速率Paris模型.结果表明,0.928 2<ρ<0.993 3,说明Paris公式也可以用来描述高温疲劳裂纹的扩展速率.

表3 X12CrMoWVNbN10-1-1钢620 ℃下疲劳裂纹扩展速率Paris模型

采用Paris公式拟合的试验关联式只与应力强度因子范围相关,不能反映应力比对疲劳裂纹扩展速率的影响.Forman公式不仅是应力强度因子范围的函数,也是应力比R函数.因此,为了更好地描述不同应力比R对裂纹扩展速率的影响,采用Forman公式对试验4,试验5,试验6数据进行拟合,结果如表4所示.

表4 X12CrMoWVNbN10-1-1钢620 ℃下疲劳裂纹扩展速率Forman模型

经典的Forman公式为:

(5)

它较好地描述了裂纹扩展的中部区和快速扩展区的裂纹扩展规律,可用来预测裂纹扩展断裂韧度Kc;同时,也可以描述不同应力比条件下的疲劳裂纹扩展速率,其拟合关系式与实验数据的相关系数比较高.

3.2 蠕变-疲劳裂纹扩展速率模型

裂纹扩展过程的载荷变化除了纯疲劳及纯蠕变之外,还存在蠕变-疲劳交互载荷,载荷不但在某段时间保持不变,而且整个载荷过程还是周期性的循环载荷.

表5为X12CrMoWVNbN10-1-1钢600 ℃下的疲劳、蠕变-疲劳裂纹扩展速率Paris模型.由表5可知,随着保载时间的增大,相关系数逐渐减小,相对误差逐渐增大.

表6为X12CrMoWVNbN10-1-1钢600 ℃下的疲劳、蠕变-疲劳裂纹扩展速率C*参数模型.由表6可知,拟合效果很好,相对误差较小.

文献[4]进行了X12CrMoWVNbN10-1-1钢600 ℃下的蠕变-疲劳裂纹扩展试验研究.本文利用文献[4]的试验数据,分别采用应力强度因子范围ΔK和裂尖参数C*对试验结果进行拟合,结果如图7所示.从图7可以看出,C*比ΔK更适合描述X12CrMoWVNbN10-1-1钢600 ℃下的蠕变-疲劳裂纹扩展速率.

表5 X12CrMoWVNbN10-1-1钢600 ℃下的疲劳、蠕变-疲劳裂纹扩展速率Paris模型

表6 X12CrMoWVNbN10-1-1钢600 ℃下的疲劳、蠕变-疲劳裂纹扩展速率C*参数模型

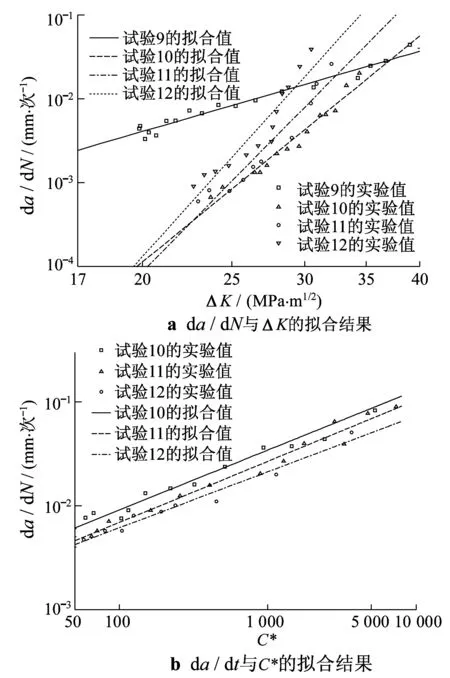
图7 裂纹扩展速率与ΔK和C*的拟合结果

4 结 论

(1) X12CrMoWVNbN10-1-1钢应力控制下高温疲劳裂纹扩展曲线呈“J”型,整个试验过程可以分为稳定扩展和加速扩展两个阶段.在稳定扩展阶段,裂纹扩展速率缓慢增加;而在加速扩展阶段,裂纹扩展速率快速增大,试样进入快速失效阶段.

(2) X12CrMoWVNbN10-1-1钢高温疲劳裂纹扩展速率随载荷、频率的增大而增大,随着应力比的增大而减小;与载荷水平、频率呈正相关,与应力比呈负相关.在载荷水平、频率及应力比3大因素中,应力比和频率对裂纹扩展的影响比较显著,频率的减小对疲劳裂纹扩展的影响也逐渐减小.

(3) 应力强度因子范围适合描述高温疲劳裂纹扩展速率,C*参数比较适合用来描述较长保

载时间的裂纹扩展速率,二者与裂纹扩展速率的双对数之间近似呈线性关系.采用Paris公式和Forman公式得出的拟合值与实验值误差较小.

[1] 吴清可.防断裂设计[M].北京:机械工业出版社,1991:1-4.

[2] 侍克献,林富生.1Cr10Mo1W1NiVNbN钢的蠕变及蠕变-疲劳裂纹扩展行为研究[J].动力工程学报,2010(4):304-308.

[3] 陈龙.考虑应变循环损伤的材料疲劳裂纹扩展行为预测方法与应用[D].成都:西南交通大学,2012.

[4] 卫东.蠕变-疲劳载荷下汽轮机转子钢X12CrMoWVNbN10-1-1的裂纹扩展试验研究[D].上海:华东理工大学,2013.

[5] SUN F,GU Y F,YAN J B,etal.Creep deformation and rupture mechanism of an advanced wrought NiFe-based superalloy for 700 ℃ class A-USC steam turbine rotor application[J].Journal of Alloys and Compounds,2016(6):389-401.

[6] CAO J,GONG Y,ZHU K,etal.Microstructure and mechanical properties of dissimilar materials joints between T92 martensitic and S304H austenitic steels[J].Materials & Design,2011,32(5):2 763-2 770.

[7] LIU X J,KONG X B,HOU G L,etal.Modeling of a 1 000 MW power plant ultra super-critical boiler system using fuzzy-neural network methods[J].Energy Conversion & Management,2013,65(1):518-527.

[8] YOSHIZAWA M,IGARASHI M,MORIGUCHI K,etal.Effect of precipitates on long-term creep deformation properties of P92 and P122 type advanced ferritic steels for USC power plants[J].Materials Science and Engineering A,2009,510(10):162-168.

[9] KOMAI N M F.Microstructural degradation of the HAZ in 11Cr-0.4Mo-2W-VNb-Cu steel (P122) during creep[J].Isij International,2002,42(12):1 364-1 370.

[10] ZHAO L,JING H Y,XU L Y,etal.Numerical investigation of factors affecting creep damage accumulation in ASME P92 steel welded joint[J].Materials & Design,2012,34:566-575.

[11] 国家质量技术监督局.GB/T 6398—2000 金属材料疲劳裂纹扩展速率试验方法[S].北京:中国标准出版社,2000:1-5.

[12] PARIS P,ERDOGAN F.A critical analysis of crack growth laws[J].Journal of Basic Engineering,1963,85:528-534.

(编辑 胡小萍)

Crack Propagation Analysis of X12CrMoWVNbN10-1-1 Steel at High Temperature

WU Zhenmao1, JI Dongmei1, ZHANG Yajie1,2, ZHU Yuemei3

(1.ShanghaiUniversityofElectricPower,Shanghai200090,China; 2.YaomengSecondPowerGenerationCompanyLtd.,Pingdingshan467031,China; 3.ShanghaiSteamTurbineFactoryofShanghaiElectricPowerStationEquipmentCo.Ltd.,Shanghai200240,China)

Crack initiation is an unavoidable problem for turbine rotors,and crack propagation shows great threat to power plant.X12CrMoWVNbN10-1-1 steel is widely used in power plants.The study mainly focuses on the crack propagation characteristics of the X12CrMoWVNbN10-1-1 rotor steel at high temperature,and the following work is carried out.The influence of load,stress ratio and frequency on crack propagation of X12CrMoWVNbN10-1-1 steel is studied through fatigue crack propagation test at 620 ℃.The crack growth rate model of X12CrMoWVNbN10-1-1 steel under high temperature of pure fatigue and creep-fatigue interaction is studied by using Paris model,Forman model and C*parameter model.The results show that the fatigue crack propagation rate da/dNof X12CrMoWVNbN10-1-1 steel under high temperature is positively correlated with the load levelPand frequencyf,but negatively with the stress ratioR.The Paris formula and Forman formula does well to describe the fatigue crack growth rate of X12CrMoWVNbN10-1-1 steel under high temperature,and the C*parameter is better to describe the creep-fatigue interaction crack propagation rate.

X12CrMoWVNbN10-1-1 steel; high temperature fatigue; creep-fatigue; crack propagation

10.3969/j.issn.1006-4729.2017.03.009

2016-11-30

吴臻茂(1991-),男,在读硕士,四川绵阳人.主要研究方向为汽轮机转子钢的力学性能.E-mail:xbrian@126.com.

TG132.3;TG115.57

A

1006-4729(2017)03-0258-07