分数阶电路的相量分析法及正弦稳态特性研究
王东东,张 波,丘东元,谢 帆
(华南理工大学电力学院,广州 510640)
分数阶电路的相量分析法及正弦稳态特性研究
王东东,张 波,丘东元,谢 帆
(华南理工大学电力学院,广州 510640)
实际存在的电感和电容事实上是分数阶元件。对于含有分数阶元件的电路,利用整数阶的方法显然无法获得准确的电路特性,且由于分数阶算子具有记忆和遗传效应,使得分数阶电路的分析繁琐复杂。因此,基于分数微积分理论,将整数阶的相量法推广应用于分数阶电路的分析中。给出了分数阶电感和分数阶电容的相量形式,分析了它们的阻抗及功率特性,研究了分数阶RLC串并联电路以及复杂分数阶电路的正弦稳态特性,探讨了分数阶元件的阶次对电路有功功率和无功功率的影响,仿真计算验证了相量法在分数阶电路中应用的正确性。
相量分析;数值仿真;分数阶电感;分数阶电容;正弦稳态特性
电感和电容是电路的基本元件。最近的相关研究表明,任何电感和电容都具有分数阶的特性,整数阶电感和电容仅是分数阶电感和电容的近似,因而采用分数微积分理论研究电感、电容将更能准确地描述它们的电压、电流关系[1-3]。然而,对于由分数阶电感、电容构成的分数阶电路,利用状态方程直接进行分析求解困难较大,为此探索分数阶电路的分析方法成为目前的一个研究方向[4-7]。
对于分数阶电路的分析目前多采用频域法,Radwan等基于分数阶频域的拉式变换分析了分数阶串联RLC电路的基本频域特性[8-10];刁利杰等采用拉式变换分析了分数阶并联RLC电路的基本特性和规律[11],但利用分数微积分的频域拉式变换法分析分数阶电路有较大的局限性,分析过程复杂,特别是在高阶电路的分析中,由于分数阶元件阶次升高,频域法所得到的结论较为复杂,难以进行解析分析;文献[12]利用频域拉式变换将分数阶微分方程变换成传递函数形式,给出了一个分数阶微分方程的形式解,解中包含了一个由特殊函数组成的和式与积式的组合,但只有在阶次较低时才能给出方程的解析表达式,不便于分析;另一方面,为了对分数阶系统进行建模分析,实际中通常利用频域近似法近似分数阶算子并对原分数阶系统进行仿真研究[13-14];文献[15]指出,通过上述仿真所得到的平衡点数目、位置等与原系统并不一定相同,因此采用频域法分析所得到的结论并不可靠。因此需要一种可以适用于高阶系统的工程应用方法来分析分数阶电路的稳态特性。
相量法是一种分析电路正弦稳态特性的方便有效的方法,在传统的整数阶电路中应用十分广泛,到目前为止,在分数阶电路的分析中并未有相应的工程实际分析方法。因此,为更方便地利用分数微积分这一精确建模分析的数学工具,本文将整数阶的相量法推广至分数阶电路的分析中,给出了分数阶电感和分数阶电容的相量形式,用相量法求解了分数阶RLC串并联电路以及更复杂分数阶电路的电压电流波形,分析了分数阶元件的阶次对电路有功功率、无功功率及功率因数角的影响,同时利用数值仿真以及基于分抗链的PSIM仿真验证了理论分析的正确性。
1 分数阶电路相量分析法
1.1 分数阶电感
对于分数阶电感L,其电压与电流的时域关系表达式为
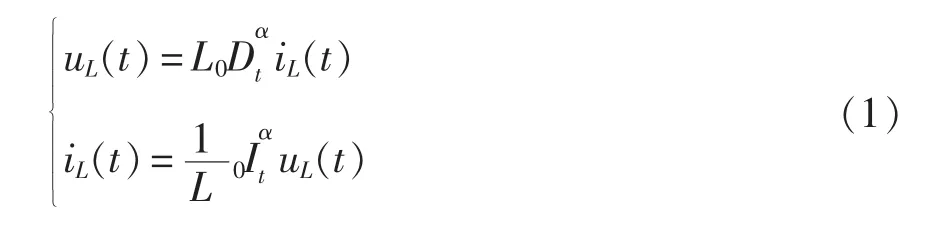
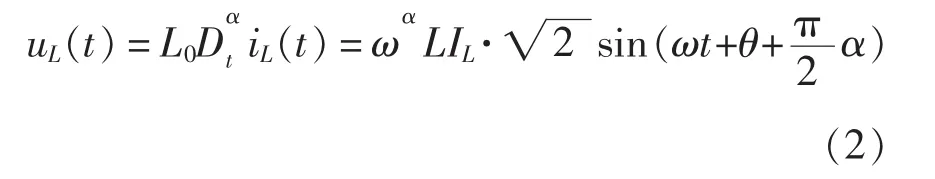
由式(2)可见,uL(t)与 iL(t)为同频率的正弦量,进一步将式(2)表示为相量形式有
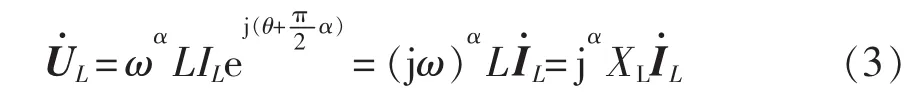
式中,XL为分数阶感抗,XL=ωαL。当分数阶次为1时,与整数阶的形式一致。式(3)对应的分数阶电感相量模型如图1所示。
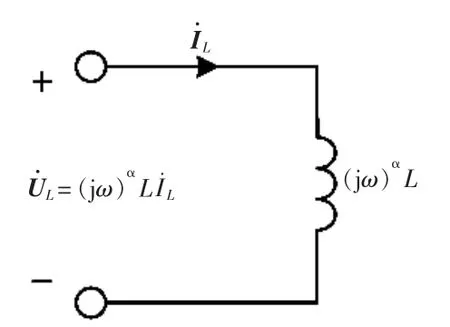
图1 分数阶电感L的相量形式电路模型Fig.1 Phasor model of the fractional-order inductor L
根据图 1、式(2)和式(3),分数阶电感的复功率可以表示为
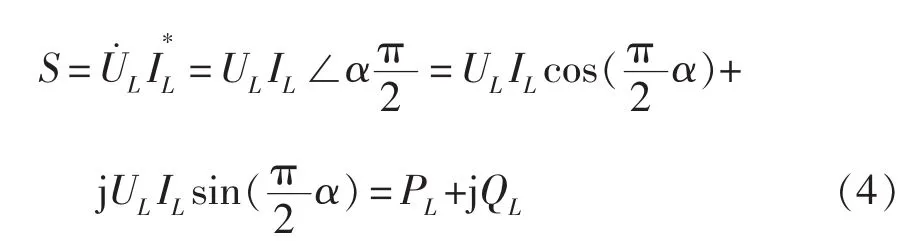
式中,PL和QL分别为分数阶电感的有功和无功功率,。 式(4)说明分数阶电感是一个带有损耗的感性无功元件,其损耗随分数阶次降低而增大,电压、电流相位关系及功率三角形如图2所示,图中,为电压、电流相位差,也是分数阶电感的功率因数角,瞬时电压uL、瞬时电流iL及瞬时功率pL(pL=uLiL)如图3所示。
1.2 分数阶电容
对于分数阶电容C,其电压与电流时域关系表达式为
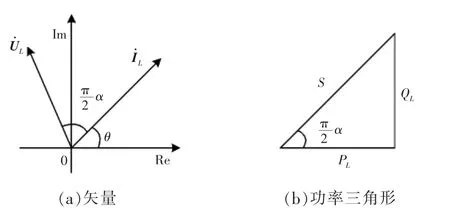
图2 分数阶电感的电压电流关系及功率三角形Fig.2 Relation ship between voltage and current and power triangle of the fractional-order inductor
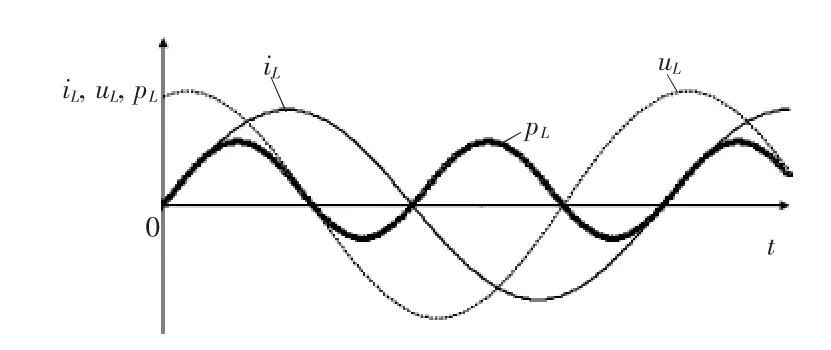
图3 分数阶电感的瞬时电压、电流及功率Fig.3 Transient voltage,transient current and transient power of fractional-order inductor
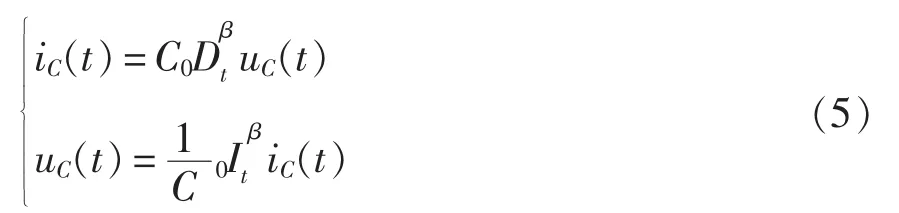
式中,β为分数阶电容阶次,取值范围为0<β<1。
假设分数阶电容电压为正弦电压,uC(t)=UC·,其相量形式为。将uC(t)代入式(5),则 C 的电流为
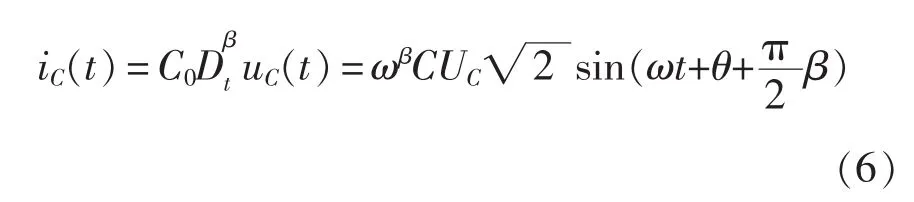
由式(6)可见,uC(t)与 iC(t)为同频率的正弦量,进一步将式(6)表示为相量形式有
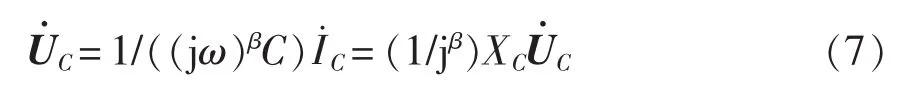
式中,XC为分数阶容抗,XC=1/((jω)βC)。 当分数阶次为1时,与整数阶的形式一致。式(7)对应的分数阶电容相量模型如图4所示。
根据图 4、式(6)和式(7),分数阶电容的复功率可以表示为
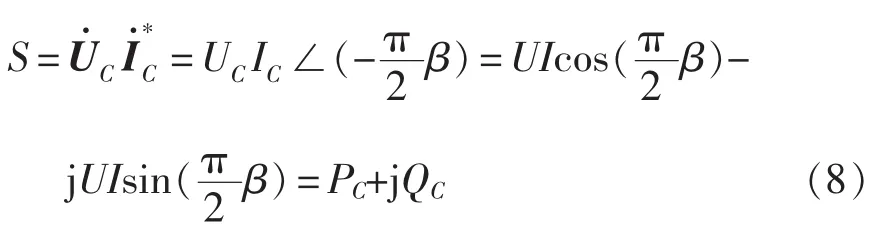
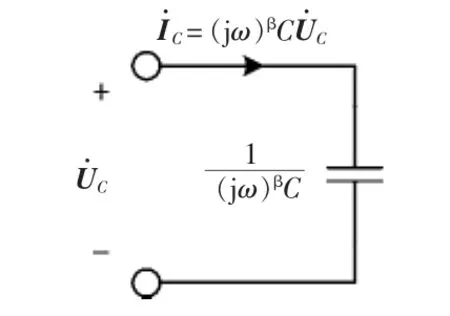
图4 分数阶电容C的相量形式电路模型Fig.4 Phasor model of the fractional-order capacitor
式中,PC和QC分别为分数阶电容的有功和无功功率,。 式(8)说明分数阶电容是一个带有损耗的容性无功元件,其损耗随分数阶次降低而增大,电压电流相位关系及功率三角形如图5所示,图中为电压电流相位差,也是分数阶电容的功率因数角,瞬时电压uC、瞬时电流iC及瞬时功率pC(pC=uCiC)如图6所示。
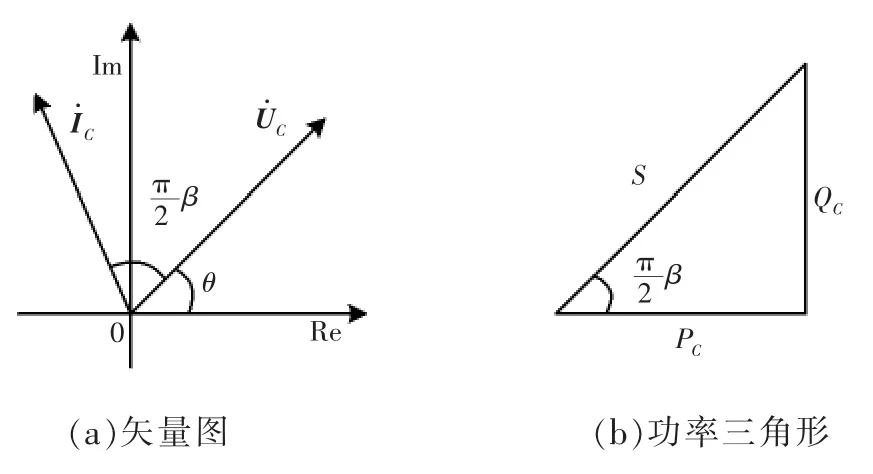
图5 分数阶电容的电压电流关系及功率三角形Fig.5 Relationship between voltage and current of the fractional-order capacitor and its power triangle
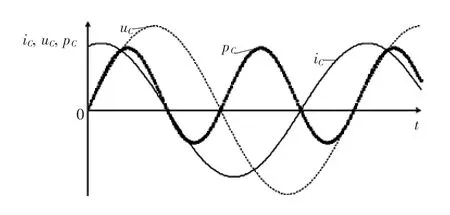
图6 分数阶电感的瞬时电压、电流及功率Fig.6 Transient voltage,transient current and transient power of the fractional-order capacitor
2 分数阶RLC电路稳态特性的相量法分析
2.1 分数阶RLC串联电路
分数阶RLC串联电路如图7所示。由基尔霍夫定律可得其时域形式的电压、电流关系为
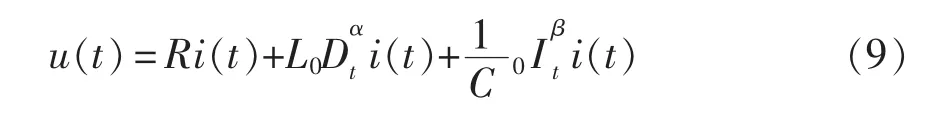

式(10)及式(11)称为分数阶RLC串联支路相量形式的欧姆定律,其电路模型如图7(b)所示。这里,当需要判断分数阶串联电路的无功分量呈感性或容性时,需要将电路总阻抗中的旋转因子jα或jβ标准化为90°旋转因子j的形式,如式(10)所示,旋转因子j前符号为正则呈感性,否则呈容性。
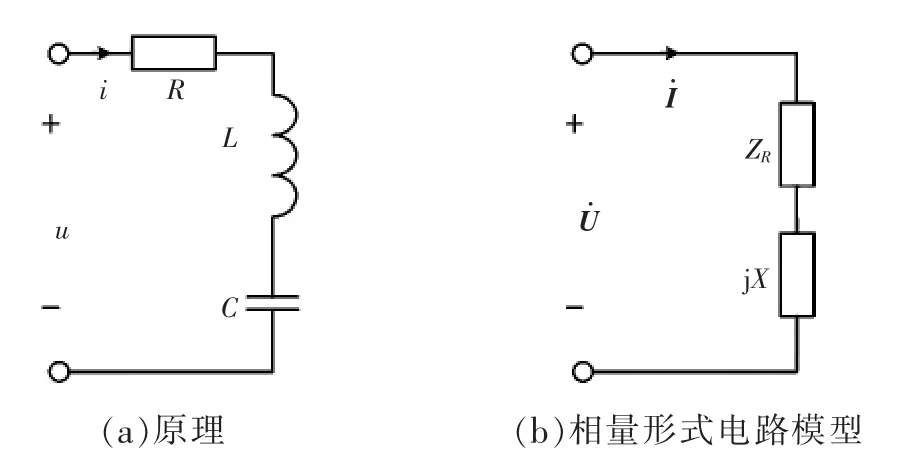
图7 分数阶RLC串联电路Fig.7 Fractional-order RLC serial circuit
对于式(10)所定义的阻抗,当 ω=0 时,ωαL=0,电感相当于短路,1/(ωβC)→∞,电路呈容性;当 ω=∞ 时,1/(ωβC)=0,电容相当于短路,ωαL→∞,呈感性;当电路发生串联电压谐振,谐振频率为
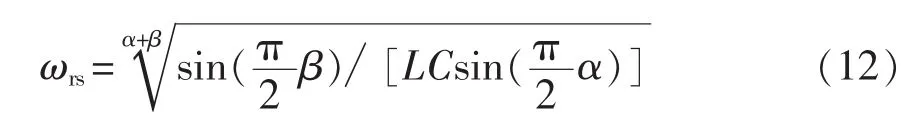
当 L=100 μH,C=470 μF,R=80 Ω,α=β=0.8,时,有°,则由相量法·sin(5 000 t+7.73°),如图 8 所示。 相量法与数值仿真波形对比结果如图 8(a)、(b)所示,由图可以看出,两者完全一致。基于分抗链PSIM仿真波形[16]如图8可得, 即(c)所示。 由图可以看出图(c)与图(a)、(b)一致。
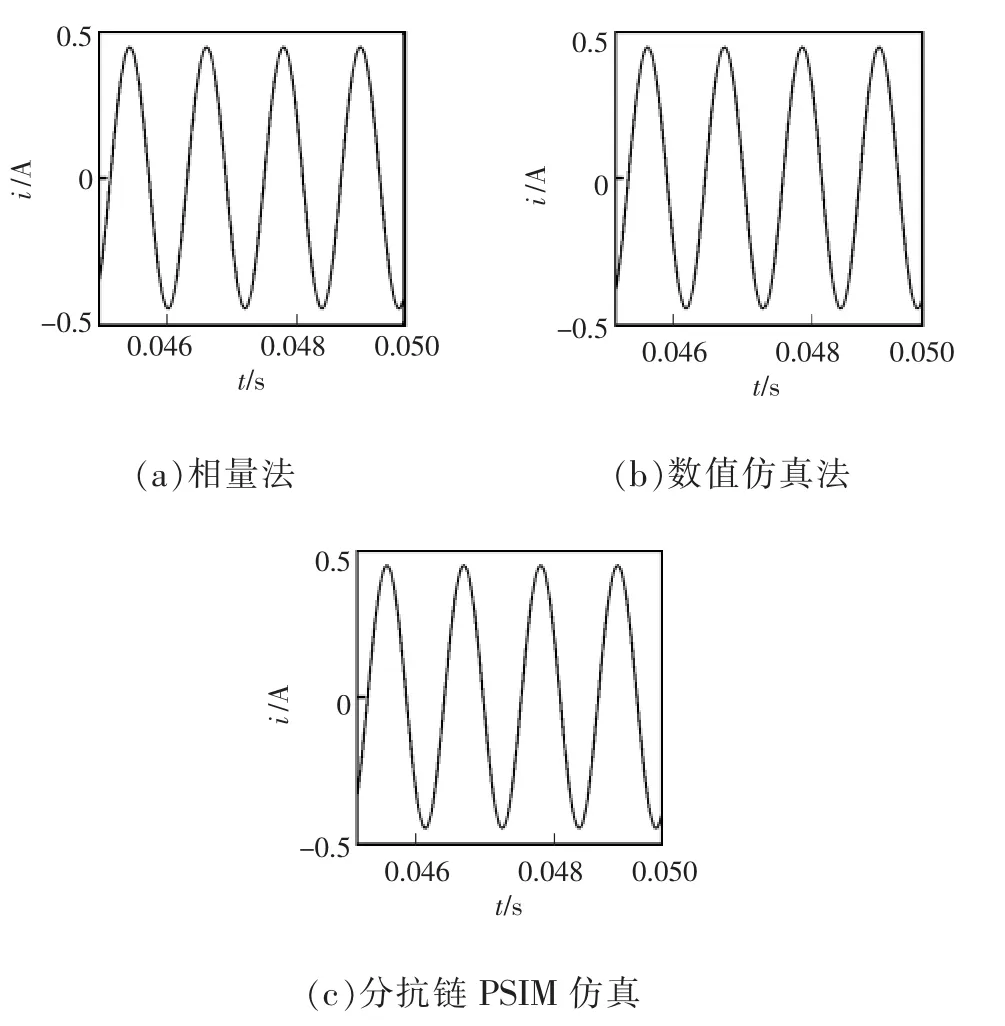
图8 分数阶RLC串联电路的电流Fig.8 Current of the fractional-order RLC serial circuit
根据式(10)可得,分数阶RLC串联电路的复功率为
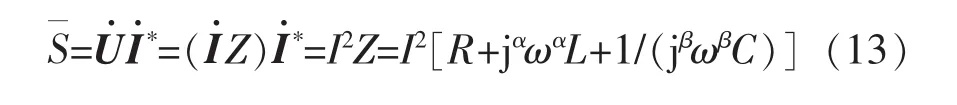
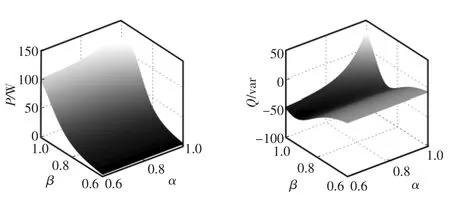
图9 分数阶RLC串联电路的有功功率及无功功率Fig.9 Active power and reactive power of the fractional-order RLC serial circuit
2.2 分数阶RLC并联电路
分数阶RLC并联电路如图10所示。由基尔霍夫定律可得其时域形式的电压、电流关系为
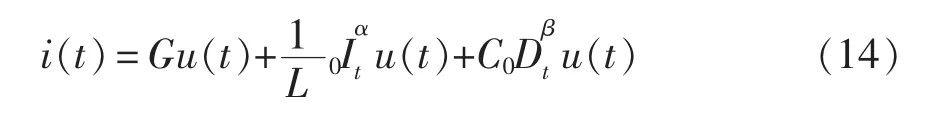
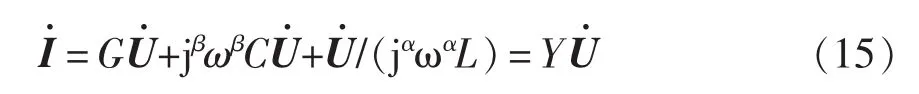
从而有

式(15)及式(16)称为分数阶RLC并联支路相量形式的欧姆定律,其电路模型如图10(b)所示。当需要判断分数阶并联电路的无功分量呈感性或容性时,需要将电路总导纳中的旋转因子jα或jβ标准化为90°旋转因子j的形式,如式(15)所示,旋转因子j前符号为正则呈容性,否则呈感性。
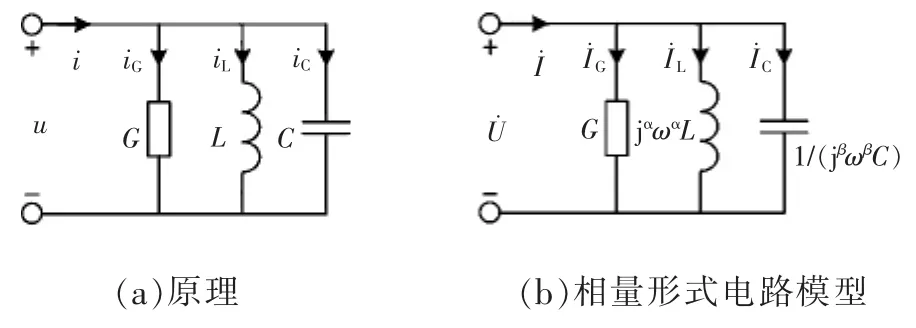
图10 分数阶RLC并联电路Fig.10 Fractional-order RLC parallel circuit
对于式(16)所定义的导纳,当 ω=0 时,ωβC=0,电容相当于开路,1/(ωαL)→∞, 为感性支路;当 ω=∞ 时,1/(ωαL)=0,电感相当于开路,ωβC→∞,为容性支路;当电路发生并联电流谐振,谐振频率为
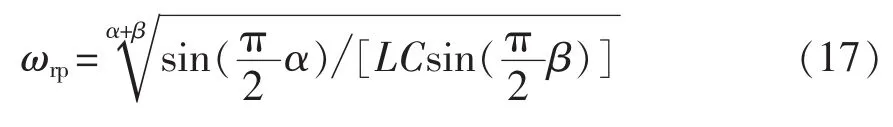
当 L=100 μH,C=470 μF,R=15 Ω,α=β=0.8,时,有°,则由相量法可得°,即·sin(5 000 t+70.34°)。相量法与数值仿真法及分抗链所得到的波形对比结果如图11所示,由图可以看出,三者完全一致。
根据式(15)可得,分数阶RLC并联电路的复功率为
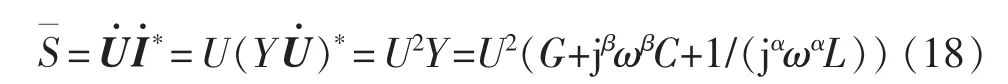
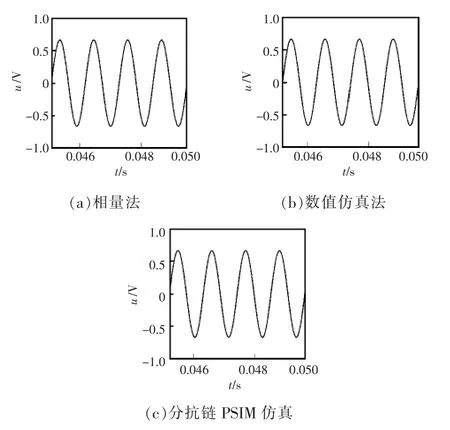
图11 分数阶RLC并联电路的电压Fig.11 Voltage of the fractional-order RLC parallel circuit
将式(18)中代入数据即可求得不同阶次下的有功功率P及无功功率Q,如图12所示。由图中可以看出,对于整个分数阶串联电路,分数阶元件的阶次降低,电路有功功率并未升高,反而有所降低。
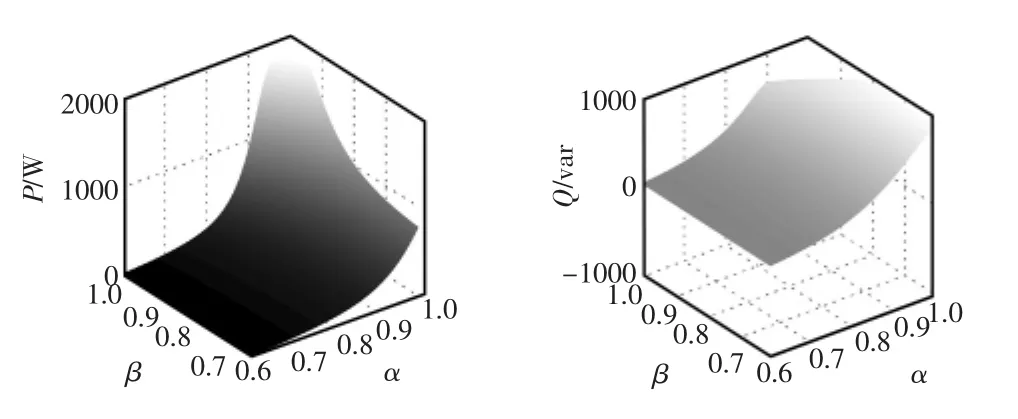
图12 分数阶并联电路的有功功率及无功功率Fig.12 Active and reactive power of the fractional-order parallel circuit
2.3 复杂分数阶电路
更为复杂的分数阶电路如图13所示,可以采用电路理论中的一般分析方法进行分析,例如网孔电流法、节点电压法等[4]。以网孔电流分析法为例进行求解。图中,30°),则以网孔电流为变量的网孔电流方程为
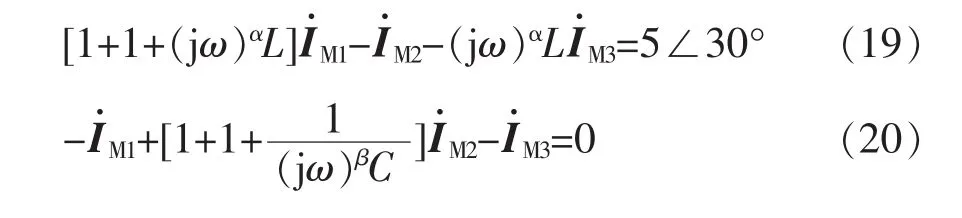
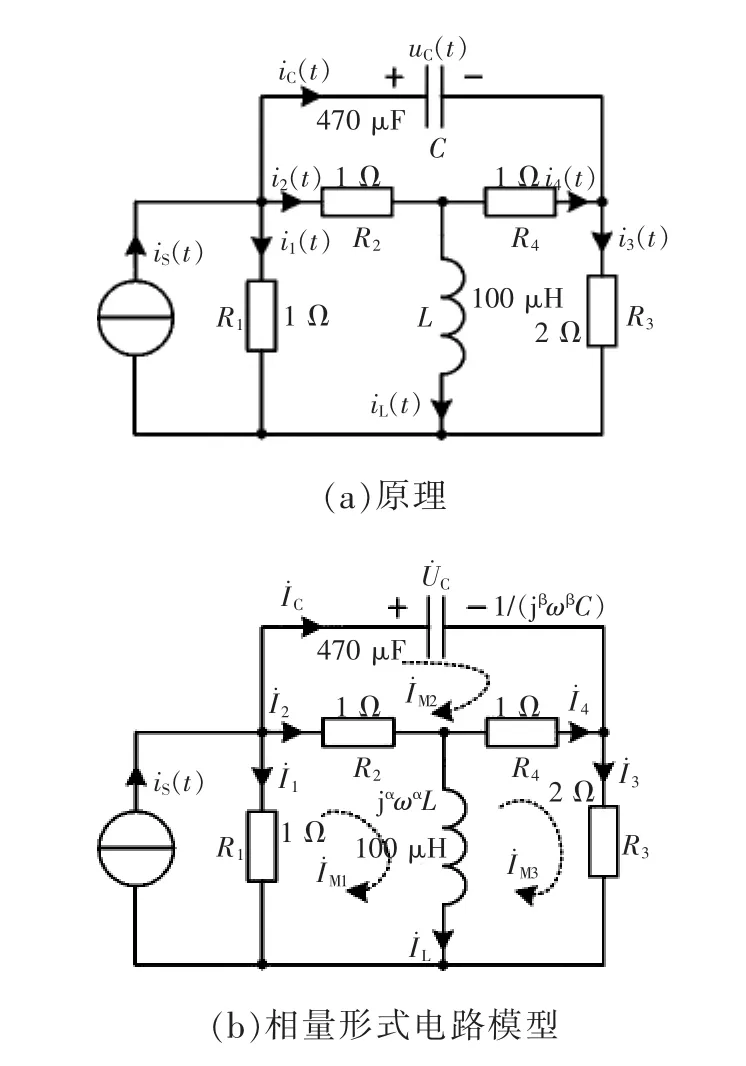
图13 复杂分数阶电路Fig.13 Complex fractional-order circuit
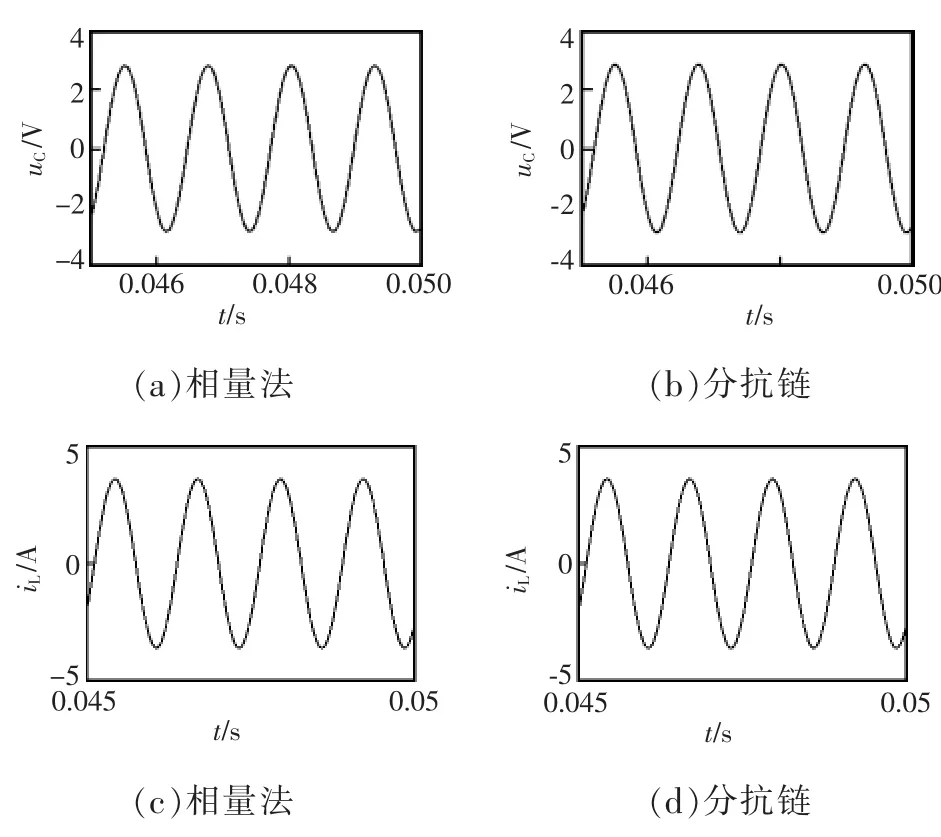
图14 复杂分数阶电路的电压uC和电流iLFig.14 Voltage uCand current iLof the complex fractional-order circuit
3 结语
相量法是分析正弦稳态电路的一种简单易行的方法,尤其对于高阶正弦稳态电路的分析具有重要意义。文中将传统整数阶的相量法推广至分数阶电路中,由于分数阶元件本质上可分解为电阻与电感或电容元件的组合,因而整数阶电路分析中所用到的定理如基尔霍夫定律以及网络分析法均可直接应用到分数阶电路的分析中。本文给出了分数阶电感及分数阶电容的相量形式,分析了它们的功率及阻抗特性,进而将所推广的相量法应用到分数阶电路中,如RLC串并联电路以及更复杂的分数阶电路等,分析了电路的正弦稳态特性以及分数阶次对于有功功率和无功功率的作用,大大降低了分数阶电路分析的复杂度,揭示了分数阶电路的本质特性,具有重要的工程实际意义。
[1]Podlubny I.Fractional differential equations[M].New York:Academic Press,1999.
[2]Westerlund S.Dead matter has memory[M].Kalmar,Sweden:Causal Consulting,2002,chapt.7.
[3]Westerlund S,Ekstam L.Capacitor theory[J].IEEE Transactions on Dielectrics and Electrical Insulation,1994,1(5):826-839.
[4]邱关源,罗先觉.电路[M].5版.北京:高等教育出版社,2006.
[5]陈崇源,孙亲锡,颜秋容.高等电路[M].武汉:武汉大学出版社,2000.
[6]Alexander C K,Sadiku M N O.Fundamentals of electric circuits[M].5thed.New York:The McGraw-Hill Companies,2013.
[7]Elwakil A S.Fractional-order circuits and systems:an emerging interdisciplinary research area[J].IEEE Circuits and Systems Magzine,2010,10(4):40-50.
[8]Radwan A G,Fouda M E.Optimization of Fractional-order RLC Filters[M].Circuits,Systems,and Signal Processing,2013,32(5):2097-2118.
[9]Radwan A G.Stability analysis of the fractional-order RLβCα[J].Journal of Fractional Calculus and Applications,2010,3(1):1-15.
[10]Radwan A G.Resonance and quality factor of the RLαCαfractional circuit[J].IEEE Journal on Emerging and Selected Topics in Circuits and Systems,2013,3(3):377-385.
[11]Diao Lijie,Zhang X F,Chen Diyi.Fractional-order multiple RLβCαcircuit[J].Acta Physica Sinica,2014,63(3):38401-038401.
[13]Carlson G E,Halijak C A.Approximation of fractional capacitors(1/s)1/nby a regular Newton process[J].IEEE Transactions on Circuit Theory,1964,11(2):210-213.
[15]Tavazoei M S,Haeri M.Limitations of frequency domain approximation for detecting chaos in fractional order systems[J].Nonlinear Analysis:Theory,Method and Applications,2008,69(4):1299-1230.
[16]Wang Faqiang,Ma Xikui.Modeling and analysis of the fractional order buck converter in DCM operation by using fractionalcalculus and the circuit-averaging technique[J].Journal of Power Electronics,2013,13(6):1008-1015.
Phasor Analysis Method and Study of Sinusoidal Steady State Characteristics of the Fractional-order Circuits
WANG Dongdong,ZHANG Bo,QIU Dongyuan,XIE Fan
(School of Electric Power,South China University of Technology,Guangzhou 510640,China)
Due to the fact that the real inductor and the real capacitor are the fractional-order components in fact,the integer-order method cannot analyze the characteristics of the fractional-order circuits accurately,and the analysis of the fractional-order circuits becomes complicated because of memory and hereditary properties of the fractional-order operator.So,based on the fractional calculus theory,the phasor method is generalized to the analysis of the fractionalorder circuits.Phasors of the fractional-order inductor and the fractional-order capacitor are given.The characteristics of the impedance and power are analyzed.The sinusoidal steady states of the fractional-order RLC circuits and the complex fractional-order circuit are studied.The influences of orders of the fractional-order components on the active power and the reactive power are analyzed.The simulation results verify the correctness of the phasor method.
phasor analysis;numerical simulation;the fractional-order inductor;fractional-order capacitor;characteristics of sinusoidal steady state

王东东
王东东(1986-),男,博士研究生,研究方向:分数微积分理论及其应用,E-mail:wangdongdongbox@126.com。
张波(1962-),男,通信作者,博士,教授,研究方向:电力电子分析与控制、电力电子系统与装置、电机与节能系统、电力电子技术在智能电网中的应用,E-mail:ep bzhang@scut.edu.cn。
丘东元(1972-),女,博士,教授,研究方向:电力电子系统非线性现象和故障诊断方法,E-mail:epdyqiu@scut.edu.cn。
谢帆(1985-),男,师资博士后,研究方向:电力电子与电力传动,E-mail:epfxie@scut.edu.cn。
10.13234/j.issn.2095-2805.2017.4.34
TM32
A
2015-12-08
国家自然科学基金重点资助项目(51437005)
Project Supported by the State Key Program of the National Natural Science Foundation of China(51437005)

