一种具有频率适应性的nk±m次谐波重复控制策略及其在四桥臂APF中的应用

周 娟，郑婉玉，刘 刚，王 超，宋振浩

（中国矿业大学电气与动力工程学院，徐州221008）

一种具有频率适应性的nk±m次谐波重复控制策略及其在四桥臂APF中的应用

周 娟，郑婉玉，刘 刚，王 超，宋振浩

（中国矿业大学电气与动力工程学院，徐州221008）

针对重复控制动态性能和频率适应性差的缺点，提出一种具有频率适应性的nk±m次谐波重复控制器，采用该重复控制器的有源电力滤波器可以选择性地补偿nk±m次谐波，满足不同应用场合的需求；与传统重复控制CRC（conventional repetitive controller）相比，该重复控制器具有延时时间小、动态响应速度快等优点。当电网电压频率波动时，该重复控制器通过采用新型有限冲激响应FIR（finite impulse response）滤波器逼近CRC内模无法实现的小数延时部分z-F，并根据电网实际频率快速调整FIR滤波器的系数，实现其对电网频率变化的适应。仿真结果验证了该重复控制器的有效性和优越性。

四桥臂有源电力滤波器；重复控制；nk±m次谐波；频率适应性

近年来，电力系统中非线性负载日益增多，产生大量谐波，有源电力滤波器APF（active power filter）可有效地补偿谐波电流［1］。补偿电流控制策略是APF的关键环节之一。由于APF的指令电流是由多次谐波叠加而成的周期信号，基于内模原理的重复控制策略［2-4］能够准确跟踪周期信号，有效提高APF的稳态性能。

针对重复控制频率适应性差的缺点，文献［5，6］提出一种采用可变一阶低通滤波器LPF（low pass filter）的重复控制方法以适应电网频率的波动，但该方法降低了系统的谐波抑制能力；文献［7］设计了一种使用FIR滤波器的重复控制方法，该方法通过实时检测电网频率，在线快速调整FIR滤波器的参数，实现对电网频率变化的适应性；文献［8，9］提出用FIR滤波器逼近小数延时部分z-F，FIR滤波器系数的计算只需少量的加法和乘法运算，可实现快速实时在线更新。因此，基于FIR滤波器的小数阶重复控制FORC（fractional order repetitive controller）在高开关频率逆变器的实时控制中提供了有效方法。

传统重复控制CRC（conventional repetitive controller）内模的输入到输出延时了一个基波周期 T0［10］，响应速度较慢，占用内存单元数至少为N（N=T0/Ts，其中，Ts为采样周期）。而在实际应用中，需要补偿的谐波主要集中在某些特定频率处，如单相整流负载的交流侧电流中仅含4k±1次谐波，三相整流负载的交流侧电流的谐波次数为 6k±1［11，12］。 采用 CRC对特定次谐波进行补偿，会导致内存浪费、补偿速度缓慢，难以满足实际系统对控制性能的要求。针对这种问题，文献［13］提出了一种奇次谐波重复控制器；文献［14，15］提出了一种 6k±1 次谐波重复控制器（6k±1）RC；文献［11，12］提出一种通用的 nk±m次谐波重复控制器（nk±m）RC以选择性地补偿谐波，该重复控制器具有时间延时小、占用内存单元少的优点。但这些特定次谐波重复控制器不具有频率适应性，尤其对（6k±1）RC而言，即使电网频率维持50 Hz不变，N/6在大部分应用场合中仍非整数［7］，从而导致系统的谐波抑制能力降低。

本文基于文献［11，12］中（nk±m）RC 的思想，设计一种具有频率适应性的nk±m次谐波重复控制器（nk±m）FARC（frequency adaptive nk±m order harmonic repetitive controller），其采用一种拉格朗日插值多项式FIR滤波器，此滤波器可逼近于由频率比值小数部分构成的延时环节。该方法既可提高（6k±1）RC在电网频率50 Hz时系统的谐波抑制能力，又可在电网电压频率波动时，根据实际电网频率在线实时调整FIR滤波器的参数，从而实现系统对电网频率变化的适应。将该重复控制器应用于带三相整流负载的四桥臂APF中，对其进行仿真验证，证明该重复控制的有效性和优越性。

1 重复控制在四桥臂APF中的应用

三相四桥臂APF的主电路如图1所示，其中，L为交流侧进线电感，R为进线电感等效电阻，ea、eb、ec为三相交流电网相电压，ia、ib、ic、in为 APF 各相补偿电流，ua、ub、uc、un分别为四桥臂变流器的交流输出电压，Vdc为APF直流侧电压。第4个桥臂的主要作用是调节有源滤波器的中线电流。

图1 三相四线制四桥臂APF的主电路结构Fig.1 Circuit structure of four-leg APF in three-phase four-wire system

根据基尔霍夫电压定律，主电路电压方程为

经拉普拉斯变换，得被控对象APF传递函数为

重复控制结构框图如图2所示。图中，N=fs/fr，其中，N为整数，fs为采样频率，fr为基波频率。

滤波器Q（z）的选择将影响重复控制器的准确性和稳定性。Q（z）的选取主要有两种：一是取接近于 1 的常数；二是采用零相移 LPF［10］，即

式中，α0、αi（i=1,2,…，m）为加权系数。该滤波器的优点是不存在相移。

补偿环节S（z）是根据被控对象P（z）的特性设计的。 为了补偿 P（z）的相位和幅值，令 S（z）=krzkC（z），其中，kr为重复控制器的增益，zk对被控对象控制延时进行补偿，C（z）对被控对象进行校正，增大系统的稳定裕度。综上所述，重复控制器的传递函数为

图2 重复控制结构框图Fig.2 Block diagram of repetitive controller

2 具有频率适应性的nk±m次谐波重复控制

2.1 nk±m次谐波重复控制器

文献［11］中设计的nk±m次谐波重复控制器的结构框图如图3所示，其离散域传递函数为

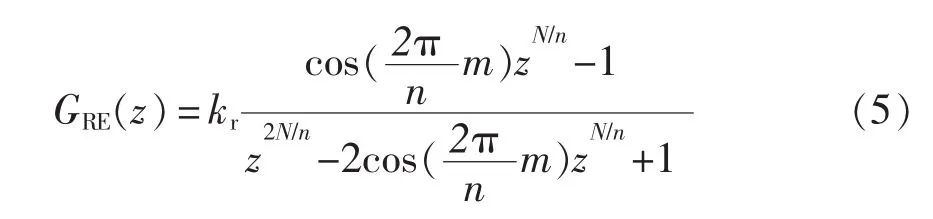
由图3可看出，（nk±m）RC的优势在于：该重复控制器最长延时时间是（2T0/n）＜T0（n＞2），在 kr一定时，其动态性能比传统重复控制器好；当n＞3时，3个延时环节占用的总内存单元数为（3N/n）＜N，因此该重复控制器占用的存储空间比传统重复控制器少。

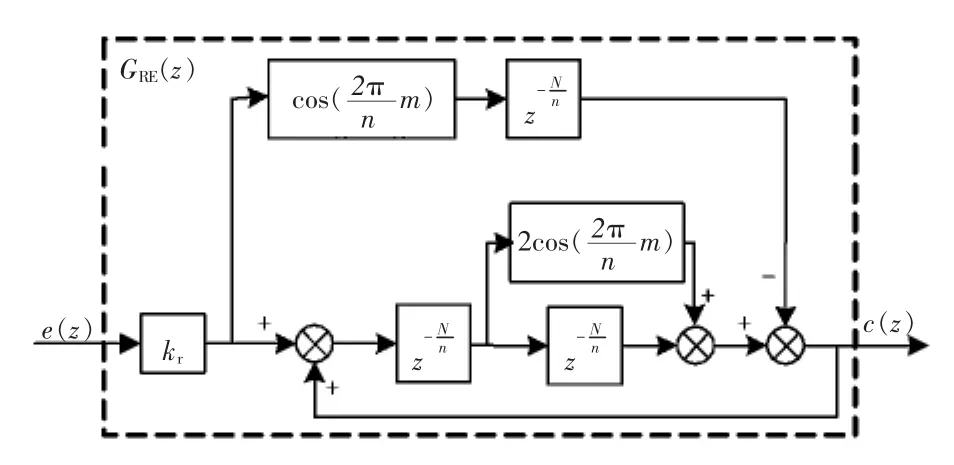
图3 nk±m次谐波重复控制器框图Fig.3 Block diagram of nk±m order harmonic repetitive controller

对6k±1次谐波进行补偿时，令n=6、m=1，因N/6在大部分应用场合中不为整数，而离散域中采用的先进先出FIFO（first in first out）单元个数只能为整数，则重复控制器的谐振频率将偏离电网实际的谐波频率，从而影响其谐波抑制能力。

图4为电网频率为50 Hz、采样频率为10 kHz时 CRC 及（6k±1）RC 的伯德图，其中滤波器取 Q（z）=（z-1+2+z）/4，图 4（b）为 CRC 及（6k±1）RC 在 550 Hz附近的幅频特性曲线。从图4（a）中可看出，与CRC相比，（6k±1）RC 可以选择性地补偿 1、5、7、11、13等次谐波，但其谐振频率与目标谐波频率都有所偏移。对图4分析可知，该（6k±1）RC在电网频率稍高于50 Hz时对谐波跟踪效果较好。

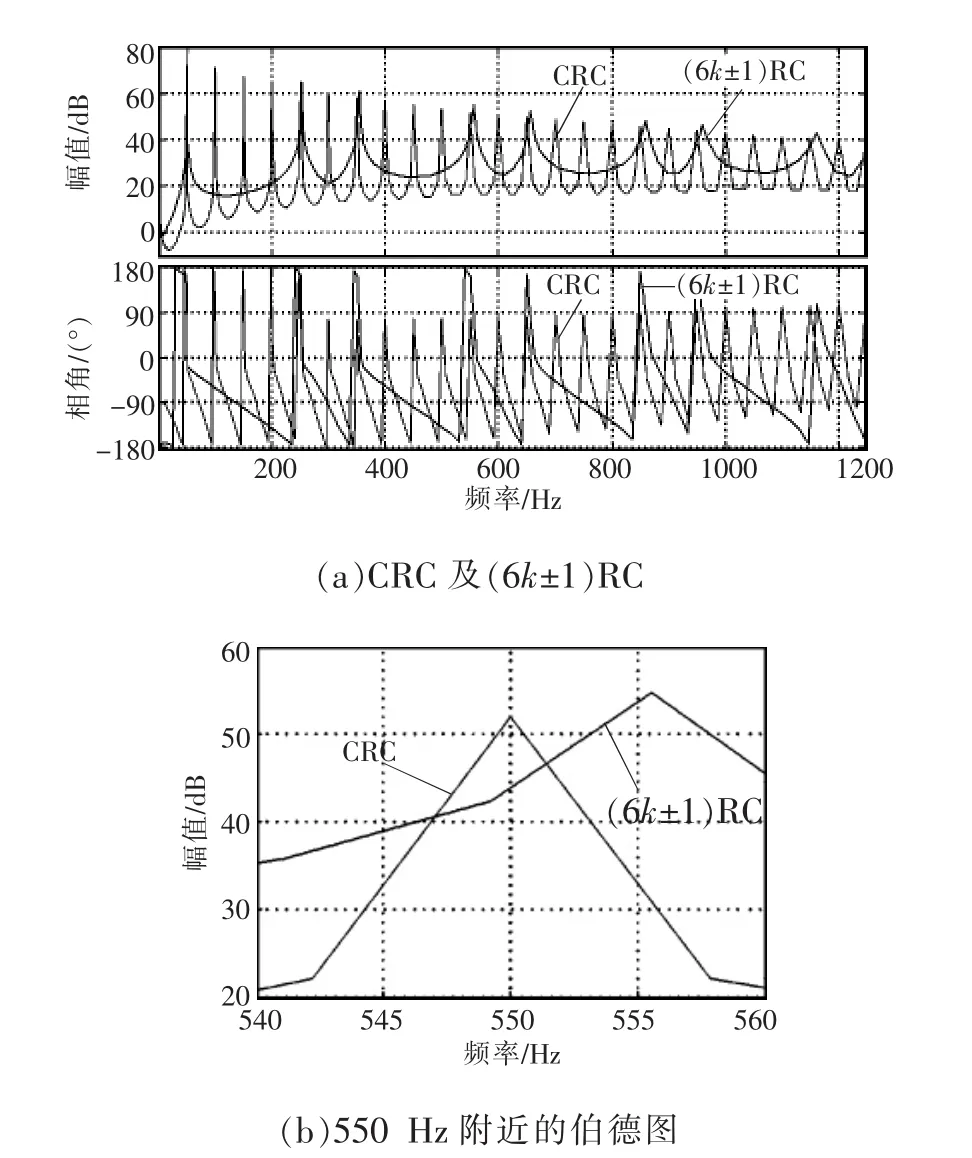
图4 CRC及（6k±1）RC的伯德图Fig.4 Bode plot of CRC and（6k±1）RC

在实际电力系统中，电网频率在一定范围内波动，（nk±m）RC的频率比值N/n不能保证为整数，从而影响系统的控制性能。

2.2 具有频率适应性的nk±m次谐波重复控制

为解决（nk±m）RC无法实现消除频率比值N/n中的小数部分而导致谐波抑制能力降低的问题，本文使用拉格朗日插值多项式FIR滤波器来逼近延时环节的小数部分。设z-N/n=z-Ni-F，其中，N/n的整数部分 Ni=int［N/n］，小数部分 F=N/n-Ni（0≤F＜1），小数延时z-F可用拉格朗日插值多项式FIR滤波器［8］表示为

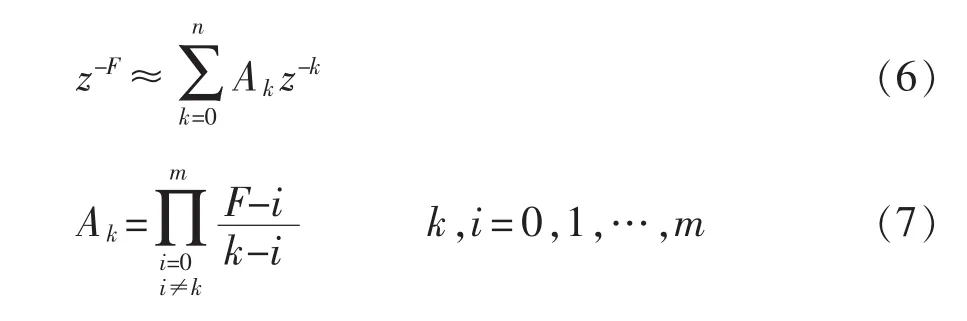
式（6）中，若令 m=1，可得 z-F≈（1-F）+Fz-1。 综合考虑滤波器参数计算的复杂度与重复控制器的稳态性能，本文取m=3，即用3阶FIR滤波器来逼近小数延时部分。FIR滤波器系数的计算只需少量的加法和乘法运算，可快速地实时在线更新。由以上分析可知，基于FIR滤波器的具有频率适应性的重复控制在APF的实时控制中提供了有效方法。

与CRC一样，为改善控制系统的稳定性和抗干扰能力，在该控制器中也需加入低通滤波器Q（z）和补偿器S（z）。图5为具有频率适应性的nk±m次谐波重复控制器的结构框图。

图5 具有频率适应性的nk±m次谐波RC框图Fig.5 Block diagram of frequency adaptive nk±m order harmonic RC

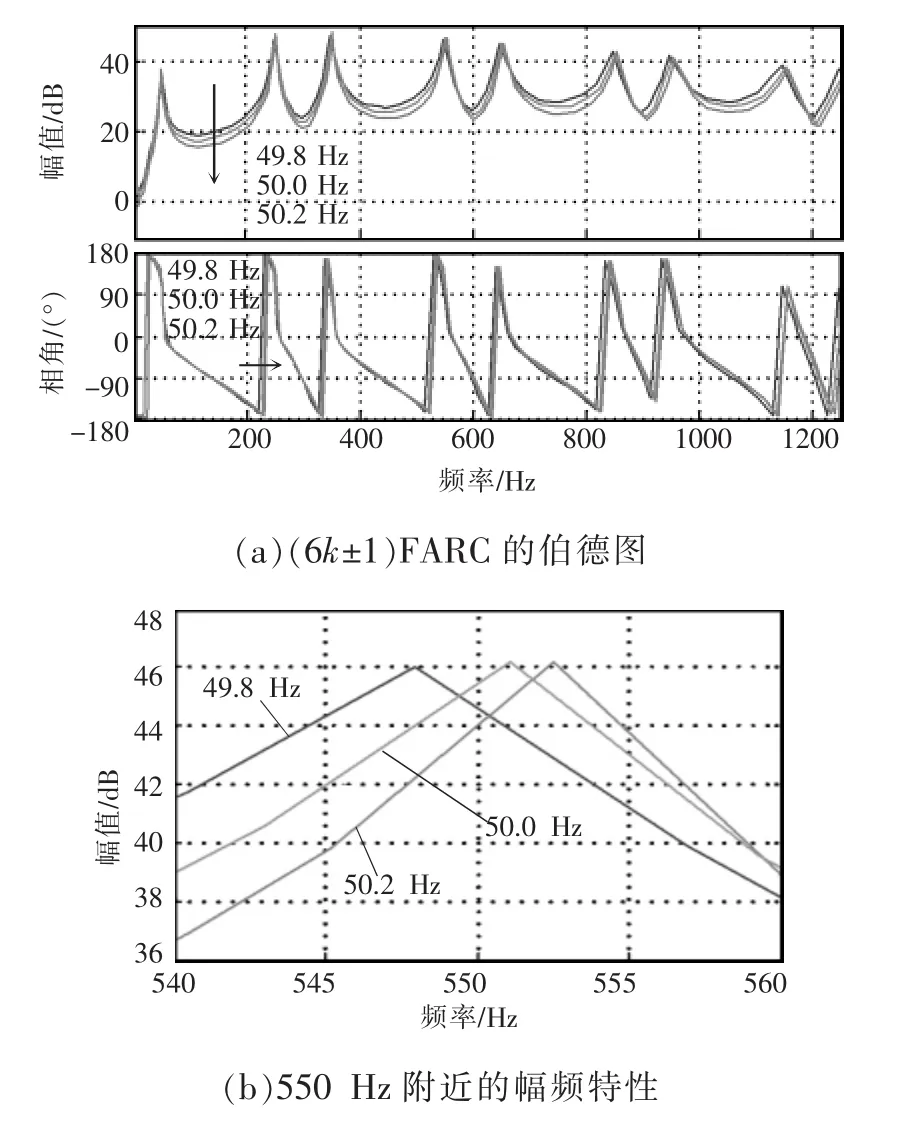
图6 （6k±1）FARC的伯德图Fig.6 Bode plot of（6k±1）FARC

图6 为采样频率为10 kHz，电网电压频率分别为49.8 Hz、50.0 Hz、50.2 Hz时， 具有频率适应性的 6k±1次谐波重复控制器FARC （frequency adaptive 6k±1 order harmonic repetitive controller）的伯德图，其中，N/6=33.5、33.3、33.2，图 6（b）为（6k±1）FARC 在 550 Hz附近的幅频特性曲线。由图6（b）可知，在电网频率分别为 49.8 Hz、50.0 Hz、50.2 Hz时，在 11 次谐波频率处 （6k±1）FARC 的谐振频率分别为 548 Hz、551 Hz、553 Hz，接近于所期望的（50±0.2）×11 Hz。

综上所述，根据不同的频率比值N/n可简单快捷地设计出此FIR数字滤波器，使其重复控制内模逼近于理想重复控制内模。本文设计的nk±m次谐波重复控制方法可通过FIR滤波器来逼近延时环节的小数部分，改善nk±m次谐波重复控制器频率比值N/n为小数而导致得谐波抑制能力降低的缺点，并且可根据电网频率的变化在线快速调整此FIR滤波器的参数，使其谐振频率与实际电网的谐波频率相吻合，从而实现对电网频率变化的适应性。

3 仿真验证

为验证本文所设计的重复控制器的有效性，在Matlab/Simulink中搭建了四桥臂APF系统仿真模型。APF主电路结构见图1，仿真参数见表1。负载为三相不可控整流器与a相电阻结合的谐波源，负载电流畸变且三相不平衡。直流侧电源采用外置电源供电。谐波检测环节采用ip-iq法［1］，采用3D-SVPWM调制策略［16］获取开关信号，补偿电流控制策略采用本文所设计的重复控制器。重复控制中滤波器取Q（z）=（z-1+2+z）/4，则根据表1参数，设计。

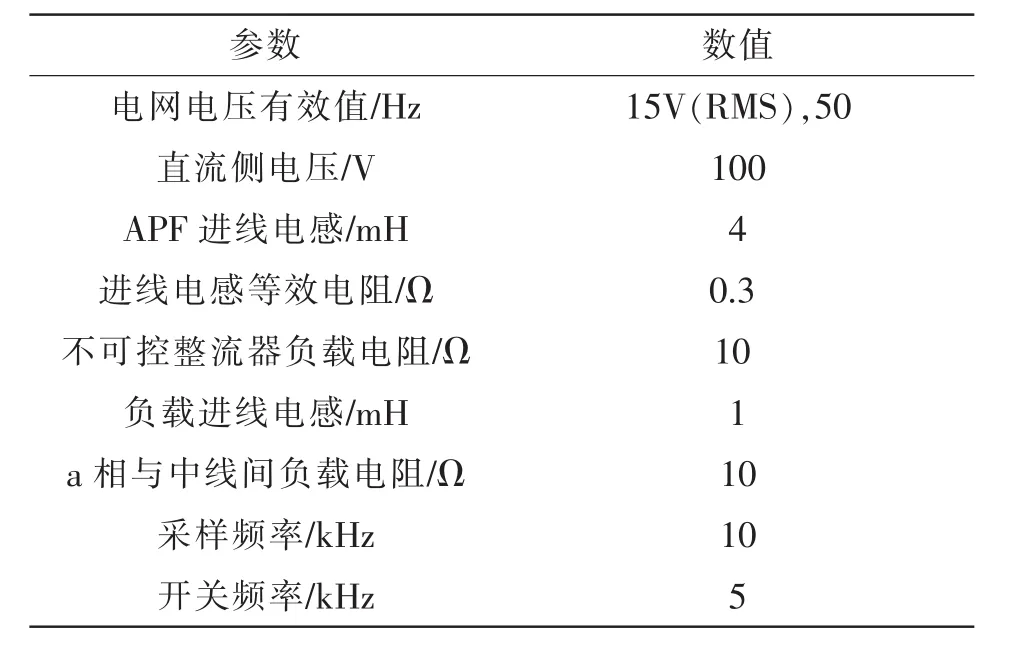
表1 仿真参数Tab.1 Simulation parameters

3.1 稳态性能分析

图7为负载电流波形及负载a相电流频谱，因a相电阻负载的存在，a相电流比b、c相电流大，三相电流总畸变率THD（total harmonic distortion）分别为 15.87%，25.78%，25.52%。

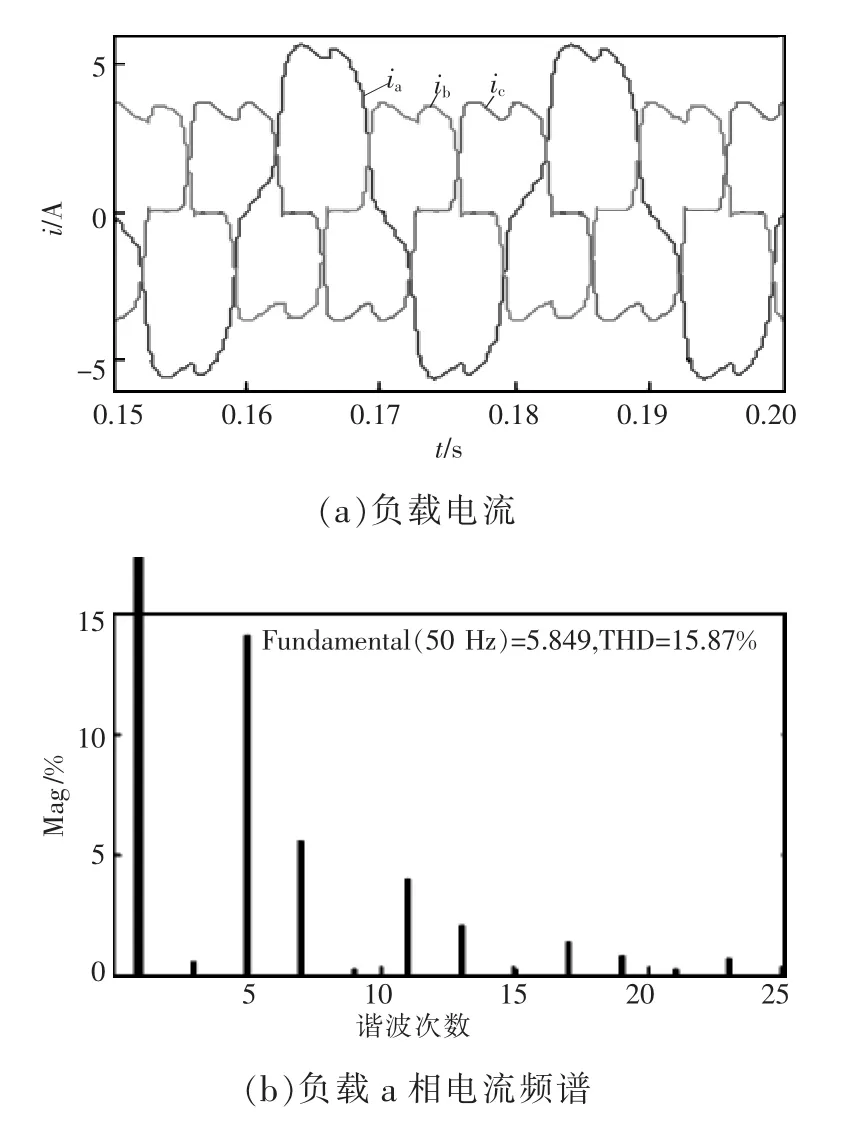
图7 负载电流波形及负载a相电流频谱Fig.7 Load currents and current spectrum of phase a

由于负载特征谐波是6k±1次谐波，APF采用的电流环控制方案是（6k±1）FARC。补偿后电网电流波形及电网a相电流频谱如图8所示，三相电流THD分别为2.58%，2.75%，2.80%，中线电流有效值由1.48 A降到0.14 A。

表2列举了在正常的电网电压频率波动范围（50±0.5）Hz 内分别采用基于 CRC、（6k±1）RC 及（6k±1）FARC的APF补偿后电网电流THD。由表2可知，CRC在电网频率波动时，与电网电压频率为50 Hz时相比，补偿后电网电流THD增大；（6k±1）RC在50 Hz时补偿后电网电流THD较CRC偏大，在50.1～50.5 Hz时补偿后电网电流THD比50 Hz时小，在49.5～49.9 Hz时补偿后电网电流THD偏大；（6k±1）FARC在所允许的电网电压频率波动范围内补偿后电网电流THD均小于（6k±1）RC。表2验证了本文所提出的（6k±1）FARC方法具有良好的稳态跟踪性能。

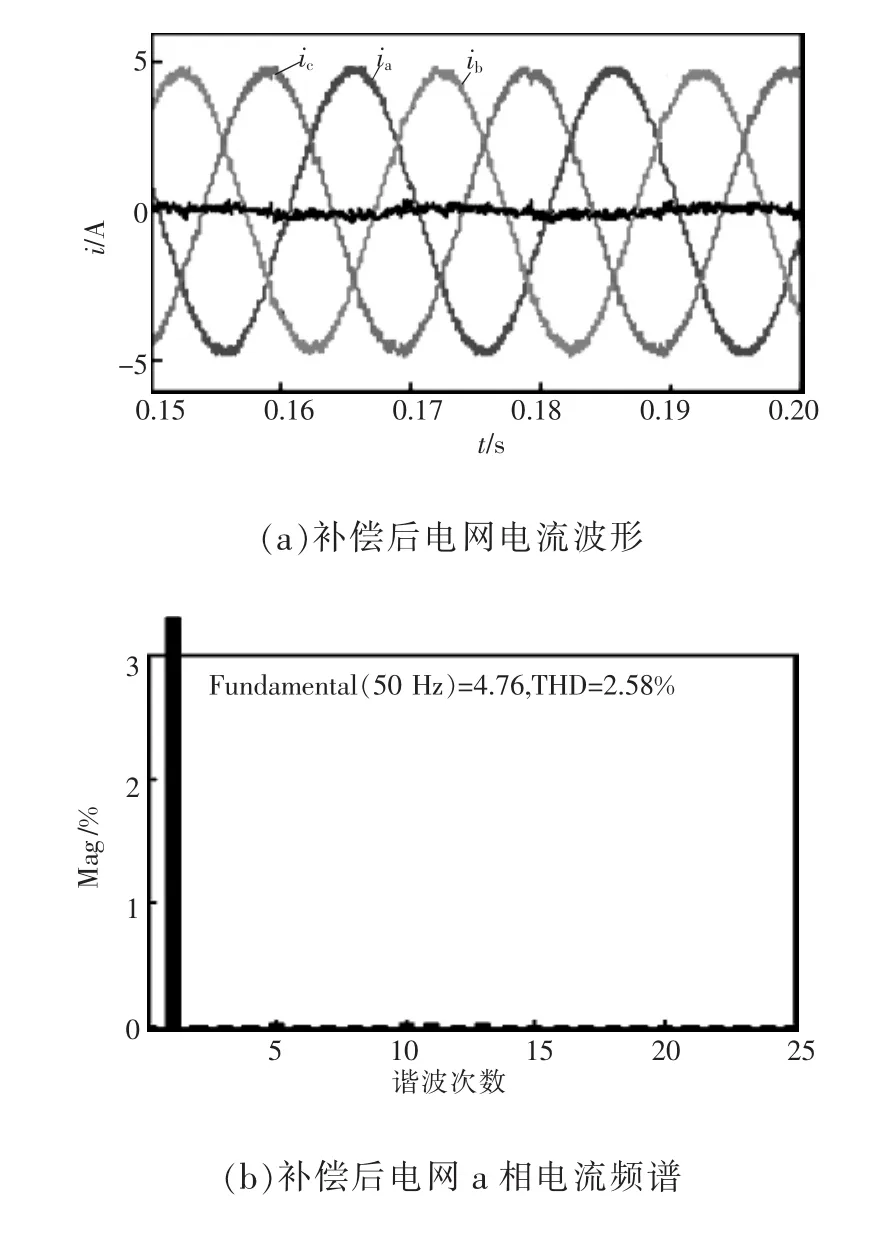
图8 补偿后电网电流波形及a相电流频谱Fig.8 Source currents and spectrum of phase a load current after compensation

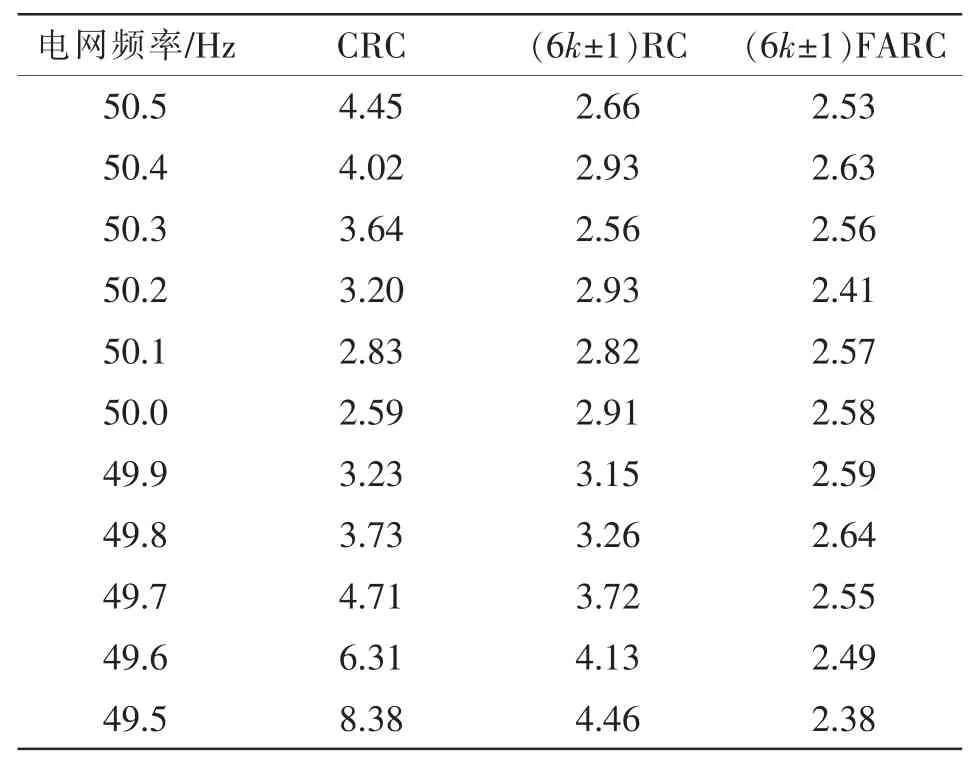
表2 不同电网频率下分别采用基于CRC、（6k±1）RC及（6k±1）FARC的APF补偿后电网电流THDTab.2 THD of source currents after APF compensation using CRC（/6k±1）RC（/6k±1）FARC under different voltage frequencies %

3.2动态性能分析

图9为采用CRC和（6k±1）FARC的a相电流跟踪误差收敛波形。 由图 9 可见，（6k±1）FARC的误差收敛速度明显快于CRC。

图9 采用CRC和（6k±1）FARC的a相电流跟踪误差收敛波形Fig.9 Current tracking error of phase a using CRC and（6k±1）FARC

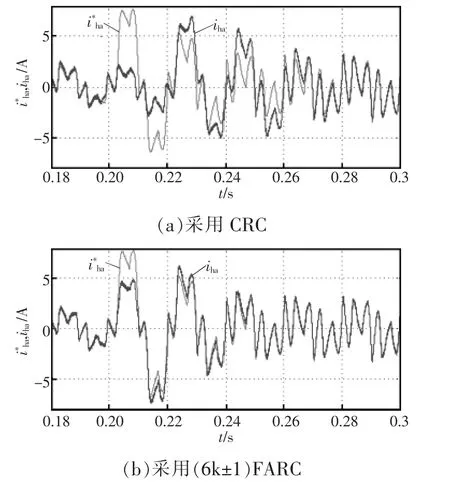
图10 突加负载时采用CRC和（6k±1）FARC a相电流跟踪情况Fig.10 Current tracking waveforms of phase a using CRC and（6k±1）FARC while load varying

在0.2 s时突加负载，分别采用 CRC和（6k±1）FARC时a相电流跟踪情况如图10所示，图中，i*ha为a相指令电流，iha为a相补偿电流。由图10可见，采用（6k±1）FARC时系统动态响应速度较快，负载突变时系统动态性能得以改善。图9和图10验证了本文所提重复控制方法的动态性能好的优点。

4 结论

（1）电网电压频率在一定范围内波动时，（nk±m）RC的频率比值N/n不能保证为整数，对于（6k±1）RC而言，即使电网频率维持50 Hz不变，N/6在大部分应用场合中仍不是整数，该特点影响了系统的控制性能。

（2）本文所设计的（nk±m）FARC 通过采用 FIR滤波器逼近CRC内模无法实现的延时环节的小数部分，改善了（nk±m）RC的性能，并实现了该重复控制器的电网频率适应性。

（3）（nk±m）FARC 的动态性能优于 CRC， 保持了（nk±m）RC动态响应速度快的优点。

［1］王兆安,杨君,刘进军,等.谐波抑制和无功功率补偿［M］.北京：机械工业出版社,2006.

［2］于晶荣,粟梅,孙尧.有源电力滤波器的改进重复控制及其优化设计［J］.电工技术学报,2012（2）：235-242.

Yu Jingrong,Su Mei,Sun Rao.Improved repetitive control and its optimization for active power filter［J］.Transactions of China Electrotechnical Society,2012,27 （2）：236-242（in Chinese）.

［3］闫士杰,冷冰,杜蘅.基于H∞重复控制的三相四桥臂逆变器研究［J］.电机与控制学报,2012,16（9）：39-47.

Yan Shijie,Leng Bing,Du Heng.Research on the threephase four-leg inverter based on H∞repetitive control［J］.Electric Machines and Control,2012,16（9）：39-47（in Chinese）.

［4]Hornik T,Zhong Qingchang.A current-control strategy for voltage-source inverters in microgrids based on H∞and repetitive control［J］.IEEE Transactions on Power Electron-ics,2011,26（3）：943-952.

［5］Hornik T,Zhong Q-C.H∞repetitive voltage control of gridconnected inverters with a frequency adaptive mechanism［J］.IET Power Electronics,2010,3（6）：925-935.

［6]Hornik T,Zhong Qingchang.A current-control strategy for voltage-source inverters in microgrids based on H∞and repetitive control［J］.IEEE Transactions on Power Electronics,2011,26（3）：943-952.

［7］陈东.并网逆变器系统中的重复控制技术及其应用研究［D］.杭州：浙江大学,2013.

Chen Dong.Research on repetitive control technique and application in grid-connected inverter systems［D］.Hangzhou：Zhejiang University,2013（in Chinese）.

［8]Nazir R,Zhou Keliang,Watson N R,et al.Frequency adaptive repetitive control of grid-connected inverters［C］.International Conference on Control,Decision and Information Technologies,IEEE,2014：584-588.

［9]Zou Zhixiang,Zhou Keliang,Wang Zheng,et al.Frequencyadaptive fractional-order repetitive control of shunt active power filters［J］.IEEE Transactions on Industrial Electronics,2015,62（3）：1659-1668.

［10］许明夏,林平,张涛,等.有源电力滤波器重复控制方法的设计［J］.电源学报,2012,10（2）：16-20,83.

Xu Mingxia,Lin Ping,Zhang Tao,et al.Design of the repetitive control method for active power filter［J］.Journal of Power Supply,2012,10（2）：16-20,83（in Chinese）.

［11］卢闻州,周克亮,杨云虎.恒压恒频PWM变换器nk±m次谐波重复控制策略［J］.电工技术学报,2011,26（5）：95-100.

Lu Wenzhou,Zhou Keliang,Yang Yunhu.nk±m order harmonic repetitive controller for CVCF PWM conveters［J］.Transactions of China Electrotechnical Society,2011,26（5）：95-100（in Chinese）.

［12］杨豪,赵军红,朱雁南,等.谐波补偿重复控制及其在逆变器控制中的应用［J］.电气传动,2013,43（8）：44-48.

Yang Hao,Zhao Junhong,Zhu Yannan,et al.Repetitive control scheme for harmonic compensation and its application in inverters［J］.Electric Drive,2013,43（8）：44-48（in Chinese）.

［13］Zhou Keliang,Low K S,Wang Yigang,et al.Zero-phase odd-harmonic repetitive controller for a single-phase PWM inverter［J］.IEEE Transactions on Power Electronics,2006,21（1）：193-201.

［14］Escobar G,Hernandez-Briones P G,Torres-Olguin R E,et al.A repetitive-based controller for the compensation of 6l±1 harmonic components［J］.IEEE Transactions on Industrial Electronics,2008,55（8）：3150-3158.

［15］Jiang Shuai,Cao Dong,Li Yuan,et al.Low-THD,fast-transient,and cost-effective synchronous-frame repetitive controller for three-phase UPS inverters［J］.IEEE Transactions on Power Electronics,2012,27（6）：2994-3005.

［16］周娟.四桥臂有源电力滤波器关键技术研究［D］.徐州：中国矿业大学,2011.

Zhou Juan.Research on the key issues of the four-leg active power filter［D］.Xuzhou： China University of Mining and Technology,2011（in Chinese）.

Frequency Adaptive nk±m Order Harmonic Repetitive Controller and Its Application in Four-leg APF

ZHOU Juan,ZHENG Wanyu,LIU Gang,WANG Chao,SONG Zhenhao
（School of Electrical and Power Engineering,China University of Mining and Technology,Xuzhou 221008,China）

To improve the dynamic performance and frequency adaptivity of repetitive control,this paper presents a frequency adaptive nk±m order harmonic repetitive controller.With proposed controller active power filter（APF） can compensate nk±m order harmonic selectively to meet the needs of different applications and gain faster dynamic response compared with conventional repetitive control（CRC）.Moreover,when the grid frequency varies slightly,by using the new type FIR filter,the proposed repetitive controller can approach the fractional part of delay segment z-Fthat conventional repetitive controller can not achieve.The parameters of the FIR filter are adjusted rapidly according to the practical grid frequency,and then the proposed repetitive controller adaptability to the grid frequency varying is achieved.Simulation results verify the validity and superiority of the proposed repetitive controller.

four-leg active power filter;repetitive control;nk±m order harmonic;frequency adaptive

周娟

周娟（1976-），女，通信作者，博士，教授，研究方向：电能质量控制、电力电子技术与应用，E-mail：zhjcumt@126.com。

郑婉玉（1992-），女，硕士研究生，研究方向：电能质量控制，E-mail：937453087@qq.com。

刘刚（1989-），男，硕士研究生，研究方向：电能质量控制、电动车电池管理系统，E-mail：gangliu@cumt.edu.cn。

王超（1991-），男，硕士研究生，研究方向：电能质量控制，E-mail：wangchao1991@cumt.edu.cn。

宋振浩（1989-），男，硕士研究生，研究方向：电能质量控制，E-mail：cumtsongzhen hao@163.com。

10.13234/j.issn.2095-2805.2017.4.10

TM46

A

2015-12-07

国家自然科学基金资助项目（51407148）

Project Supported by National Natural Science of Foundation of China（51407148）