百变弹簧，功能制胜

江苏 傅思远

百变弹簧，功能制胜

江苏 傅思远

百变，说的是弹簧的弹力和弹性势能善变，涉及的问题很多。弹簧问题常常涉及胡克定律、动能定理、功能关系，而功能关系能一锤定音，克敌制胜。

【例题】如图1所示，水平桌面上的轻质弹簧一端固定，另一端与小物块相连。弹簧处于自然长度时物块位于O点（图中未标出）。物块的质量为m，AB＝a，物块与桌面间的动摩擦因数为μ。现用水平向右的力将物块从O点拉至A点，拉力做的功为W。撤去拉力后物块由静止向左运动，经O点到达B点时速度为零。重力加速度为g。则上述过程中 （ ）

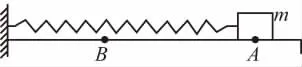
图1

A．物块在A点时，弹簧的弹性势能等于

B．物块在B点时，弹簧的弹性势能小于

C．经O点时，物块的动能小于W－μmga

D．物块动能最大时弹簧的弹性势能小于物块在B点时弹簧的弹性势能

【第一印象】

（1）题干中已知AB的距离为a，却不将O点的位置在图中标出，所以潜意识认为判断O点位置或许就是解题的突破口。

（2）物块与桌面间的动摩擦因数为μ，在运动过程中存在阻力作用，这无疑增大解题的难度和复杂性。

（3）初看物体的运动可分为两个过程：O→A和A→B。但分析选项C时发现并不如此简单，还应将A→B过程分为A→O和O→B两个过程。

方法一：【解析】为了更清楚地说明情况，画出位置示意图如图2所示。

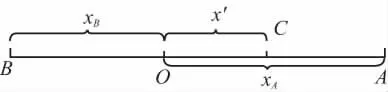
图2

如果没有摩擦力，则O点应该在AB中间，由于存在摩擦阻力，物体从A到B过程中机械能损失，故无法到达没有摩擦力情况下的B点，即O点应靠近B点。故有OA＞，此过程物体克服摩擦力做功大于，所以物块在A点时，弹簧的弹性势能小于，A项错误；由A项分析得物块从开始运动到最终停在B点，路程大于a＋，故整个过程物体克服阻力做功大于，所以物块在B点时，弹簧的弹性势能小于，B项正确；从O点开始到再次到达O点，物体路程大于a，根据动能定理得物块的动能小于W－μmga，故C项正确；物块动能最大时，弹力大小等于摩擦力。而在B点，弹力与摩擦力的大小关系未知，故物块动能最大时弹簧伸长量与物块在B点时弹簧压缩量大小未知，故此两位置弹性势能大小关系不好判断，所以D项错误。

【答案】BC

【启迪】上述解法亮点是巧妙利用反证法迅速判断O点并非AB连线的中点。再运用功能关系和动能定理分别分析相应过程的弹性势能、动能的大小关系。除此之外，还有让人脑洞大开的思路和方法吗？

令k＝100 N/m，小物块的质量m＝1 kg，小物块与桌面的动摩擦因数μ＝0．4，则滑动摩擦力为f＝μmg＝4 N，动能最大位置的弹簧伸长量为

当用水平向右的力将物块从O点拉至A点，应该有xA＞x′，撤去拉力后物块才能由静止向左运动，并且若能使小物块过O点时速度大于0，需，则xA＞2x′，设xA＝0．1 m，则拉力做功0．9 J。

所以经O点时，物块的动能为Ek＝EpA－μmgxA＝

解得xB＝0．02 m（舍去负值）

则物块在B点时，弹簧的弹性势能为

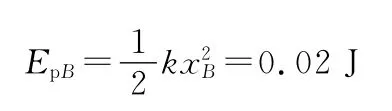
故a＝xA＋xB＝0．12 m。

对于题中四个选项逐个判断

选项A：物块在A点时，弹簧的弹性势能等于EpA＝

选项B：物块在B点时，弹簧的弹性势能EpB＝0．02 J，

选项C：经O点时，物块的动能为Ek＝0．1 J，而W－μmga＝0．42 J，故Ek＜W－μmga，C项正确；

选项D：物块动能最大时，弹簧的弹性势能Epmax＝，大于物块在B点时弹性势能EpB＝0．02 J，所以D项错误。

通过上述的分析求解可总结如下特点：

（1）通过例题可以看出，解决弹簧问题，分析弹簧的形变是关键，确定弹簧的形变及变化情况，结合受力分析、动能定理、功能关系是解决问题的突破口；

（2）弹簧的弹性势能与劲度系数、形变量有关，一般情况不需要计算大小，只要弹簧的形变量相同时，弹性势能就相同，运算过程中可以替代或约去，省去烦琐的计算。

（作者单位：江苏省六合高级中学高三12班）