二轮数理融合需自我加压的几个方面

湖北 朱木清

二轮数理融合需自我加压的几个方面

湖北 朱木清

高考物理“五种能力”中，应用数学处理物理问题的能力，是考查区分的重点。为应对这一问题，各校一般会在二轮后期安排一个专题复习。但仅依赖一次短期突击是远远不够的，重要的还在于激发内在动力，把提升数理融合目标变成个体的自觉行动，贯穿于全过程，落实到训练中。为此，建议同学们在以下几个方面自我加压。

一、主动梳理物理解题常用的数学知识和方法

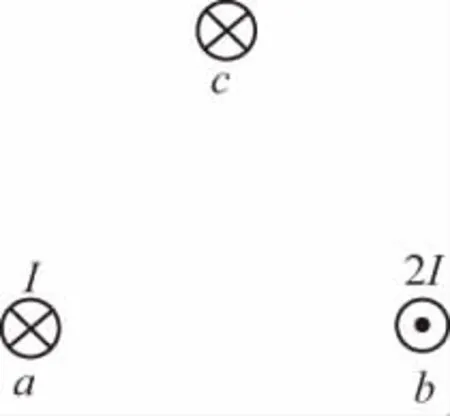
图1

【解析】先分析导线a的受力，题设a、b平行，电流分别为I和2I，此时a受到的磁场力大小为F。再在a、b的上方放置一根与a、b平行的通电长直导线c，a、b、c正好构成一个等边三角形，a受到的磁场力大小仍为F，根据平行四边形定则，可知c对a的磁场力Fca方向由a指向c，大小等于F，如图2所示。

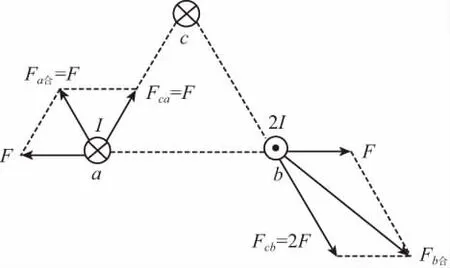
图2

再分析b的受力，a对b的磁场力大小为F，因为rca＝rcb，a、b电流分别为I和2I，所以c对a的磁场力大小Fca＝F，故c对b的磁场力大小Fcb＝2F，根据平行四边形定则和余弦定理，可得b受到的磁场合力大小为Fb合＝，D项正确。

【答案】D

【点评】矢量的平行四边形定则本身就是一个几何图形。本例要用到余弦定理，在解题中不常用。课标卷物理注重数学知识应用的广度和深度，淡化烦琐数学计算，代数方程、函数分析、解析几何、三角函数、指数对数、导数微分等均已渗透物理教材，几何法、图象法、极限极端法、极值法、微元法、转化法、半定量与估算法等数学方法成为高考的“常客”，若将这些数学知识方法做些梳理，具体细化，解题很给力。

二、重视解题中辅助关系方程的分析

【例2】水平面上A、B、C三点固定着三个电荷量均为Q的正点电荷，将另一质量为m的带正电的小球（可视为点电荷）放置在O点，OABC恰好构成一棱长为L的正四面体，如图3所示。已知静电力常量为k，重力加速度为g，为使小球能静止在O点，小球所带的电荷量q为 （ ）

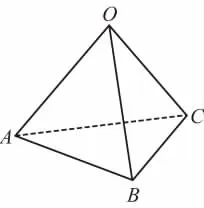
图3

【解析】O处小球受到A、B、C三个点电荷的库仑力大小均为，方向沿正四面体侧棱，将库仑力F正交分解，根据平衡条件和对称性，它们的水平合力为零，竖直合力跟小球重力平衡。

设F与水平方向夹角为α，有3Fsinα＝mg，如图4所示，底面垂心H到顶点A或B的距离，联立解得

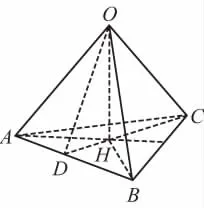
图4

【答案】C

【点评】本题牵涉到正四面体侧面与底面所成的二面角，侧棱与底面的夹角α，容易误以为都是60°，混淆侧棱与底面夹角与二面角关系，从而错选A项或B项。物理解题经常涉及这样的辅助关系。平时练习中，常见到所列物理方程都对，但辅助方程卡壳或出错，十分可惜。因此，列辅助方程非但不能小视，而且在接下来的训练中还应加强。

三、重视物理难点中的数学破解以及数学对物理的诠释

【例3】如图5所示，小车用跨越定滑轮的轻绳牵引提升井下重物。某时刻小车和物体的速度大小分别为v1和v2，加速度大小分别为a1和a2，细绳与水平地面夹角为θ，则下列关系式正确的是 （ ）

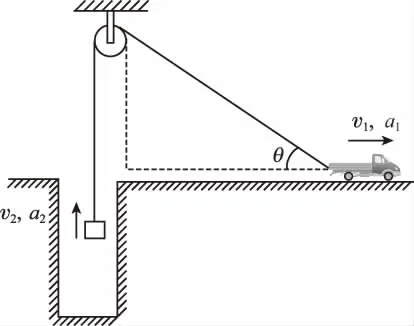
图5

A．v1cosθ＝v2B．v1＝v2cosθ

C．a1cosθ＝a2D．a1＝a2cosθ

【解析】设时间Δt内小车向右的位移为Δx，斜绳长度变化为Δs，物体提升高度变化Δh＝Δs，斜绳倾角变化Δθ，如图6所示，故有 Δxcosθ＝Δs，等式两边同除以 Δt，并取Δt→0，得v1cosθ＝v2，A项正确，B项错误。

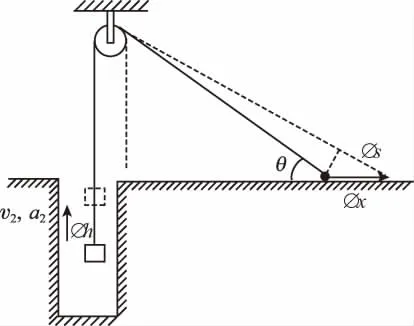
图6

在关系式v1cosθ＝v2中，v1、v2和θ均随时间t变化，等式两边同时对时间t求导，有

【答案】A

【点评】我们知道，对有转动的绳或杆，两端牵连体沿绳或杆方向的分速度总等大，但加速度关系就不那么简单，也是个“擦边球”，上述数学推导结果给我们以启示：小车的运动可看成两个分运动：一是以滑轮为中心、斜绳长为半径的变速圆周运动（速度的大小和方向都变化），另一是沿斜绳伸长或缩短方向的运动。

如图7所示，小车的加速度分量a1cosθ方向沿绳方向，但它并不等于斜绳的伸长或缩短产生的沿绳方向加速度分量ar，还包含了绕滑轮做变速圆周运动的向心加速度分量an，二者的矢量和满足a1cosθ＝ar－an。

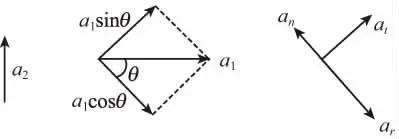
图7

需注意，当绳有转动，牵连体垂直绳方向的分速度不为零时，因绕定滑轮转动存在向心加速度（方向沿绳向），重物的加速度a2与小车的加速度沿绳方向的分量a1cosθ不等，二者加速度关系为a2＝a1cosθ±an（式中符号“±”跟小车加速运动的方向有关，如小车向左加速，则取“＋”号）；仅当绳无转动，牵连体垂直绳方向的分速度为零时，才有两端牵连体沿绳方向加速度分量等大。

【例4】如图8所示，在xOy平面内的y轴右侧，虚线包围圆形区域为真空，圆半径为L，圆心在O1（2L，0）处，x＝0～3L区间除虚线包围圆形区域，其余部分有垂直纸面向外的匀强磁场，磁感应强度为B。一质量为m、带电量为＋q的粒子从y轴某点垂直y轴射入磁场，不计粒子重力作用。

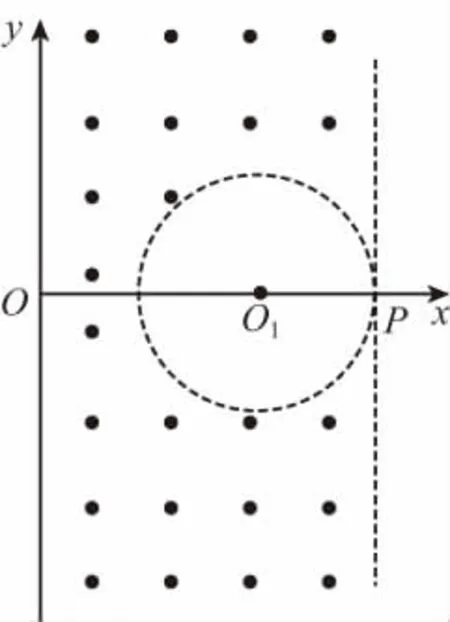
图8

（1）若粒子经过x轴上P点，求其入射的位置和速度大小；

（2）若粒子经过圆形区域中心O1点，求入射速度最小值。

【解析】（1）粒子在匀强磁场中做匀速圆周运动，有

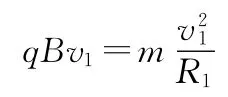
若粒子经过x轴上P点，则入射的位置坐标为（0，3L），圆轨道半径R1＝3L，入射速度大小

（2）若粒子经过圆形区域中心O1点，必是先在磁场中做一段圆弧运动，再沿真空圆半径方向匀速运动到O1点，设粒子圆弧运动的轨道中心为O2，轨道半径为R，圆弧中心角为θ，几何位置关系如图9所示，同理有

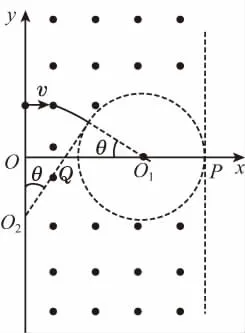
图9

欲v最小，必须R最小，而

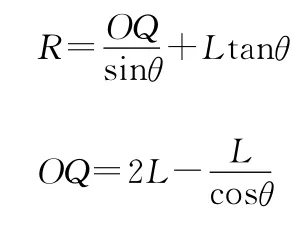
【点评】求解物理极值题，通常有物理和数学两种方法，但本题必须借助数学方法。同学们对三角函数求极值、二次函数求极值、均值不等式求最值等方法玩得都很酷，但这里求分式函数极值是个难点，导函数为零是否能想到？物理问题的分析过程，就是数学方法的运用过程，数学用活了，物理也活了。

（作者单位：湖北省武汉市黄陂区第一中学）