平抛运动与圆周运动有关知识的结合在生活中的应用

贵州 胡朝平

平抛运动与圆周运动有关知识的结合在生活中的应用

贵州 胡朝平

平抛运动与圆周运动知识相结合的问题在现实生活中有很多事例，解决这类问题要分析研究各阶段的独立性，其中两相邻过程中的速度是联系两过程的纽带，运用平抛运动规律和圆周运动有关规律，同时结合图形中的几何关系分析，下面以力学中常见的情况进行分析。

一、物体运动由平抛运动变化到竖直圆周运动

【例1】如图1所示，是某次四驱车比赛的轨道中某一段，小华控制的四驱车（可视为质点），质量为m＝1．0 kg，额定功率为P＝7 W。小华的四驱车到达水平平台上时，启动四驱车的发动机并直接使发动机的功率达到额定功率，一段时间后关闭发动机。当四驱车由平台边缘P点飞出后，恰好从光滑圆弧ABC的A点的切线方向进入圆弧（不计空气阻力，进入圆弧时无机械能损失）。已知圆弧的半径R＝0．3 m，θ＝60°，赛车到达A点时的速度vA＝4 m/s（取g＝10 m/s2）。求：

图1

（1）赛车做平抛运动的初速度v0；

（2）P点与A点的水平距离和竖直高度；

（3）赛车到达圆弧最高点C时对轨道的压力。

【解析】（1）赛车到A点的速度如图2所示，赛车做平抛运动的初速度v0等于vA的水平分速度，由图可知v0＝vx＝vAcosθ＝4×cos60°＝2 m/s。

（2）由图可知，赛车运动至A点时竖直方向的分速度为

设P点与A点的水平距离为x，竖直高度为h，则

图2

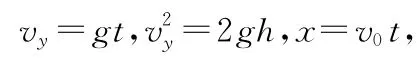
联立以上几式解得

x≈0．69 m，h＝0．6 m。

（3）取A点为重力势能的零点，由机械能守恒定律得

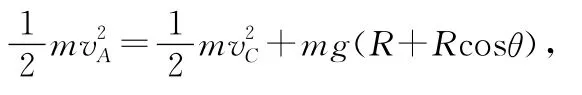
设赛车到达圆弧最高点C时，轨道对它的弹力为FN，由圆周运动向心力公式得

代入数据得FN≈13．3 N，

由牛顿第三定律可知，赛车对轨道的压力大小F′N＝FN＝13．3 N，方向竖直向上。

【评析】物体运动由平抛运动变化到竖直圆周运动，分析时，应按如下步骤：

（1）画好图示，明确图中几何关系，运用数学知识找出相关量之间的关系；

（2）抓住速度是联系前后两个过程的关键物理量，前一过程的末速度是后一过程的初速度；

（3）列出平抛运动有关规律（包括速度、位移、角度关系式）；

（4）若利用功能关系解答问题时，要特别注意两种曲线运动结合处的速度情况。若速度分解，有能量损失，若没有速度分解，可以利用全过程法解决。

二、物体运动由圆周运动变化到平抛运动

【例2】如图3所示的S形玩具轨道，该轨道是用内壁光滑的薄壁细圆管弯成，放置在竖直平面内，轨道弯曲部分是由两个半径相等的半圆对接而成，圆弧半径比细管内径大得多，轨道底端与水平地面相切，轨道在水平方向不可移动。弹射装置将一个小球（小球的直径略小于细圆管内径）从a点沿水平地面向b点运动并进入轨道，经过轨道后从最高点d水平抛出。已知小球与地面ab段间的动摩擦因数为μ，ab段长为L，圆的半径为R，小球质量为m，求：

图3

（1）若小球经d处时，对轨道上壁有压力，则它经过b处时的速度满足什么条件？

（2）为使小球离开轨道d处后，不会再碰到轨道，则小球离开d处时的速度至少为多大？

【解析】（1）小球经过d处时，对轨道上壁有压力，向心力由重力和轨道上壁压力提供，根据牛顿第二定律，小球经d点时得

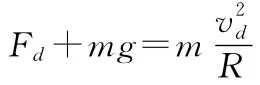
小球经d处对轨道上臂有压力Fd＞0

小球从b到d，由机械能守恒定律得

（2）设小球离开d处时的速度为vd，在运动过程中与轨道恰好相碰，即小球的运动轨迹与圆相切。以d点为坐标原点建立如图4所示坐标系，由平抛运动规律得

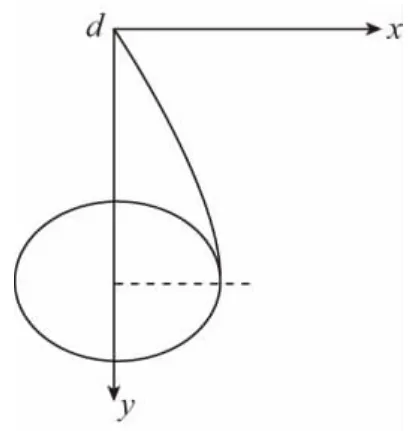
图4

由①②两式得

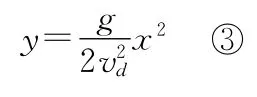
由解析几何知识得

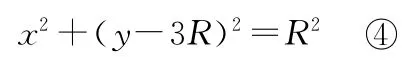
联立③④两式得

要使得抛物线与圆相切，则方程⑤的Δ判别式为零，

故小球离开轨道d处后，不再碰到轨道，小球离开d出时的速度至少为

【评析】物体运动由竖直圆周运动变化到平抛运动，分析这类情况分析时，有以下步骤：

（1）明确竖直面内的圆周运动是“轻杆模型”还是“轻绳模型”，分析物体能够到达圆周最高点的临界条件；

（2）物体在竖直圆周运动最高点或最低点求作用力时，找到指向圆心的向心力，运用牛顿第二定律列方程式Fn＝man分析；

（3）光滑轨道上的圆周运动运用机械能守恒定律，有摩擦的圆周运动运用动能定理或能量守恒定律分析；

（4）画好圆周运动与平抛运动图示，明确图中几何关系，运用数学知识（包括几何关系、三角函数和解析几何知识）找出相关量的关系；

（5）列出平抛运动有关规律求解。

（作者单位：贵州省天柱民族中学）