偏心轴随动磨削数学模型的研究

范晋伟，张兰清，邬昌军，刘凯凯

（北京工业大学 机械工程与应用电子技术学院，北京 100124）

偏心轴随动磨削数学模型的研究

范晋伟，张兰清，邬昌军，刘凯凯

（北京工业大学 机械工程与应用电子技术学院，北京 100124）

针对偏心轴随动磨削中存在的加工精度问题，通过建立随动数控磨床运动之间的数学模型推导出理想的砂轮切削点的轨迹方程并进行MATLAB仿真，根据随动磨削运动特性推导出磨削设计约束方程，并分析了偏心轴在恒线速度加工条件下砂轮中心位移变化值，为了保证砂轮磨削点与摆轴颈的任意加工点相切，对相关参数并进行离散化，且对运动方程进行了有效修正，为后续误差补偿做铺垫，以达到提高加工精度的目的。

偏心轴；加工精度；随动磨削；数学模型；

0 引言

如今工业机器人开始逐渐运用于各个领域，其发展质量和水平很大程度上代表一个国家的工业发达水平[1]。偏心轴作为工业机器人关节处RV减速器中的核心部件[2]，一般用于低速或静止调节位置，要求体积小，加工精度高。因此其加工质量和加工效率直接制约着工业机器人的发展。RV减速器偏心轴随动磨床是磨削偏心轴的工作母机如图1所示，对其自身的精度要求更高，然而磨床自身的磨损和人为因素误差影响远远高于零件表面粗糙度误差的影响，成为影响整体零件的加工质量的主要因素，所以必须采取有效措施加以解决。

磨床的各运动部件存在的动静态误差是影响加工精度的根源，要对这些误差进行有效的补偿，首要问题就是建立精确的数控机床空间误差模型。1967年French和Humphries等首先用三角关系法建立起了三轴机床的几何误差模型[3]。1986年Donmez[4]等人提出了一种通用误差建模和补偿的方法。1990年Elshennaway等人用刚体运动学对测量机的几何误差进行了建模分析[5]。1993年Kiridena等用机构学法建立了RRTTT、RTTTR、TTTRR等形式的五坐标机床的空间几何误差模型，此后这种方法被较广泛地用于各种多轴机床的空间几何误差建模[6]。浙江大学的邬义杰[7]研究了多面形随动轴的磨削成形原理及数控加工技术，根据磨削速度相对的原则建立了磨削运动方程，推出了针对多面形非圆曲面磨削的插补算法递推公式。华中科技大学谢胜泉[8]建立了砂轮跟踪控制模型，并研究出新的跟踪控制算法。上海机床厂有限公司采用西门子公司的840D开放式数控系统和611D数字式交流伺服驱动器，通过植入随动磨削控制软件对数控系统进行二次开发，研制了H405-BF汽车曲轴随动跟踪磨床[9]。江西杰克机床有限公司的“数控高速随动曲轴磨床”系列中，JKM8240数控高速随动曲轴连杆颈磨床和JKM8140数控高速随动曲轴主轴颈磨床具有自主知识产权[10]。而现如今针对随动式RV减速器偏心轴的磨床研究还很少，但最近北京第二机床厂初有成效，生产了一套整机设备，机床整体技术达到国际领先技术水平，但在加工精度上还需进一步有效提高。本文通过数学建模，并从砂轮磨削点运动轨迹、跟踪磨削设计约束方程、恒线速度下砂轮中心位置变化，建立几何关系进行求解，并进行MATLAB仿真，找出误差来源，为误差补偿做铺垫，并应用于实践生产之中。

图1 偏心轴随动磨床三视简图

1 砂轮磨削点的运动轨迹

偏心轴磨削加工过程中，偏心轴绕主轴颈中心O旋转，同时砂轮沿着X轴方向做往复跟踪运动，使得砂轮在磨削时始终与摆轴颈保持相切，保证摆轴颈加工的形状。如图2随动磨削运动示意图，以主轴颈中心O为圆点，建立X-O-Y坐标系，以砂轮中心点O1为坐标原点，建立X-O1-Y坐标系，X轴正方向均为砂轮远离偏心轴方向。通过坐标系对工件与砂轮的切点进行描述。切点在曲轴主轴坐标系上的数学表达为加工工件时所有磨削切点位置，而切点在砂轮中心坐标系的位置表达为磨削点的运动轨迹。

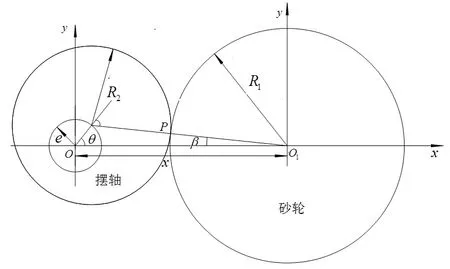
图2 偏心轴随动数控磨削数学模型

假设初始条件下，偏心轴相对于水平轴的旋转角度为0，偏心轴转过角θ后根据上图在X-O-Y坐标系中，由三角函数关系式可得出切点p坐标(Xp,Yp)表达式为：

在三角形OO1O2中三角形正弦定理简化可得：

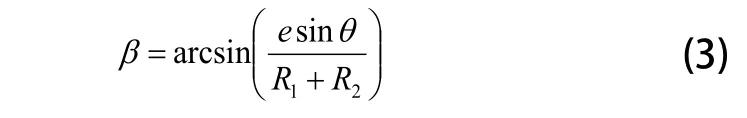
而在XO1Y坐标系中有：

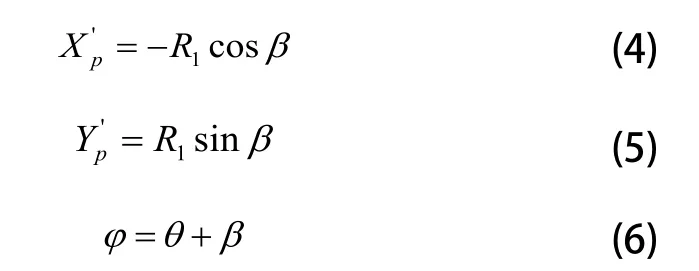
在三角形O1O2中，利用正弦定理得：

联立式(6)、式(7)可得：

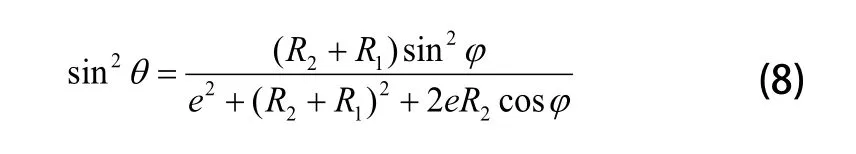
令e=2mm，R1=30mm，R2=300mm，利用MATLAB画出摆轴轴径在磨削过程中所有切点位置在X-O-Y中的轨迹图像。由图3知，其图形近似为椭圆。

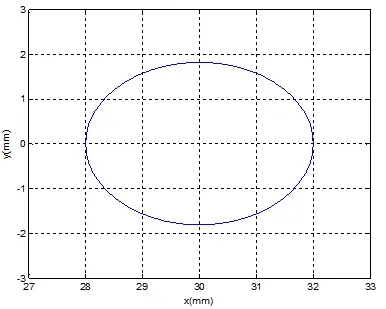
图3 砂轮安装误差与加工误差关系图

在图中，封闭曲线上的任意一点与坐标原点的连线与水平轴正向的夹角（逆时针）表示对应时刻偏心轴的转动角度。由图中可以看出，工件在磨削加工过程中，砂轮与工件的切点是不断变化的，这种情况对工件的尺寸大小，形状精度，表面粗糙度，波纹度，磨削力等都会产生影响，所以，保证磨削点的运动轨迹在精密加工中非常重要。

2 跟踪磨削设计的约束方程

分别以偏心轴心轴中心，摆轴中心，砂轮架中心建立与各自部件固连的坐标系为X1O1Y1，XbObYb，X2O2Y2，并且在心轴中心建立固定不动的大地坐标系X0O0Y0，如图4所示。

图4 偏心轴随动数控磨削数学模型

当位于初始位置时，所有坐标系坐标轴都与大地坐标系平行，坐标系X1O1Y1，X2O2Y2，XbObYb原坐标分别为（0，0），（L，0），（e，0），砂轮可沿X轴平行移动，位移量参数为x，偏心轴可绕心轴中心转动，转角为1。设在摆轴中心坐标系中有一个起点（0，0），终点为任意点P的矢量r，其与摆轴中心坐标系Xb的夹角为2θ，则任意点P在摆轴中心坐标系中的坐标为：

根据坐标变换原理，任意点P在偏心轴心轴中心坐标系中的坐标为：

任一点P在大地坐标系中的坐标为：

砂轮中心在大地坐标系的坐标为：

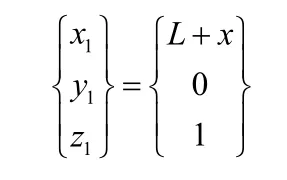
现在大地坐标系中令任意点P与砂轮中心相重合，得到偏心轴加工过程的瞬时方程：

于是首先求得砂轮在某一瞬时相对于其初始位置的位移量为：

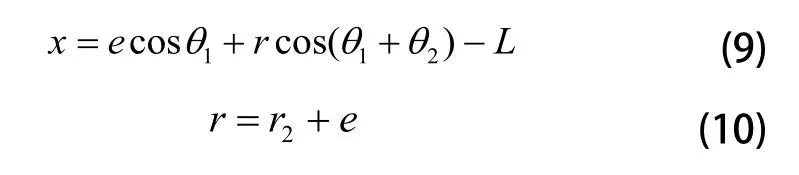
在摆轴中心坐标系中，砂轮绕摆轴中心的转角为：

在摆轴中心坐标系中，砂轮绕摆轴中心的转动速度为：

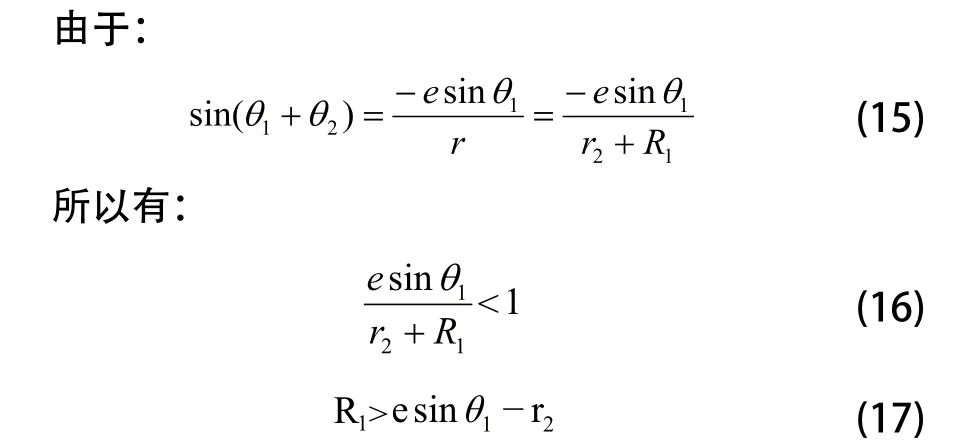
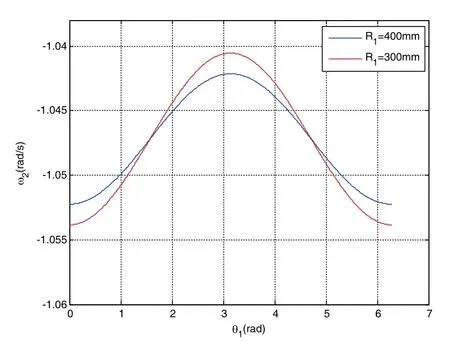
图5 不同砂轮绕摆轴中心转速对比图

3 偏心轴恒线速度条件下建模与分析

由于主轴头架采用恒转速运动过程中，摆轴上的磨削点相对于转动中心的速度和受力状态是时刻变化的，因此为想实现偏心轴精密磨削，应该采取主轴在旋转过程中应为变速运动，且工件磨削点相对于摆轴中心为恒线速度运动，砂轮架进行对应旋转角度的往复跟踪运动，才能达到精密磨削的加工要求。

图6 磨削点在摆轴上的运动轨迹

图6 中，A点为曲轴转角θ为零时的磨削点，P为任意时刻的加工点，弧AP为曲轴磨削点的运动轨迹，其圆弧长度记为S，则：

对式(19)两边求积分，并整理得：

由于头架为非恒转速度运动，这里n用来表示头架旋转的平均转速，且式(20)满足以下边界条件：

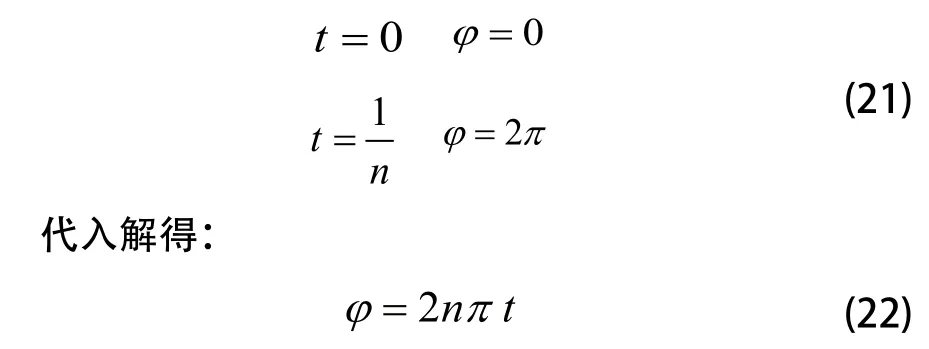
如图6所示，在三角形OO1O2中，由余弦定理知：

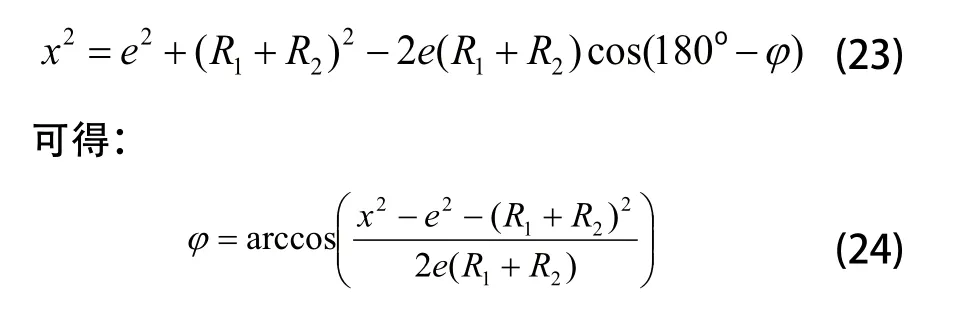
砂轮中心O1到主轴颈中心O的距离为x，则：

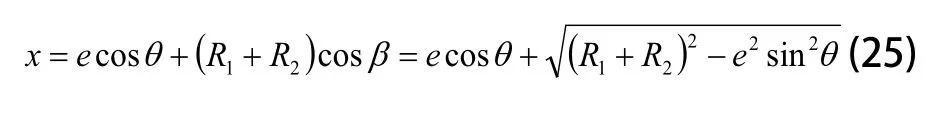
令偏心轴尺寸e=2mm，R1=30mm，R2=300mm，在恒线速度磨削的条件下，工件坐标系内偏心轴任意转角的砂轮中心点位置如图7所示，其描述了偏心轴旋转一周过程中，砂轮中心位移值变化规律图像。

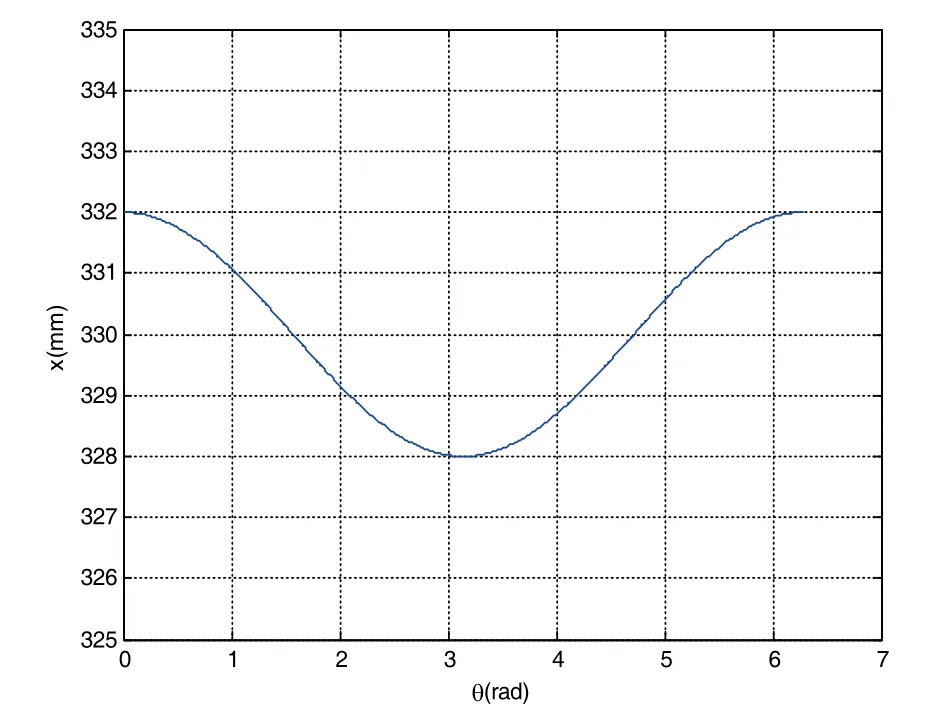
图7 随动磨削X轴运动曲线

利用式(25)，以1°或0.5°（离散采样区间）为采样周期，对磨床头架旋转一周范围内值进行离散化，得到相应的x值，即数控系统发出指令驱动位置信息。

试验设3个处理，3次重复，随机区组排列，小区面积8 m2。垄宽50 cm，沟宽30 cm，株距20 cm，密度12.45万株/hm2。生长期视墒情浇水，莲座期、结球期分别随浇水追施尿素1次，每次用量为225 kg/hm2。苗期中耕锄草，其他按常规管理。

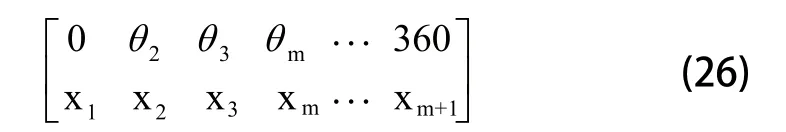
又式(22)与式(24)联立，得：

通过上述的数据列表，可以获得一系列的加工数据点，原则上θ值的离散区间越小，加工误差就会越小，但在实际加工中，取小的离散区间会为数控系统带来繁琐，过大区间会导致较大的轮廓误差。因此需要有一个合理的采样区间选择标准来方便工程人员参考。

4 偏心轴运动方程修正

由式(25)和式(28)确定的运动方程可知，在磨削摆轴颈时，被磨表面各点的磨削厚度会随偏心轴转角变化，为了让磨削过程中任意时刻的当量磨削厚度相等有必要对运动模型进行修正。依照“磨削点在摆轴颈上匀速运动的原则”确定偏心轴的变速转动不作调整，而是对砂轮中心的水平位移x叠加一个修正位移量来抵消运动方程导致的误差。由当量磨削厚度公式可知：

式中ap为磨削深度；vw为工件上磨削点的速度；vs为砂轮上磨削点的速度。

由于磨削点在摆轴颈上匀速运动，则vw、vs均视为常量，当量磨削厚度只与磨削深度有关。则在任意时刻磨削点法向深度可由以下公式计算：

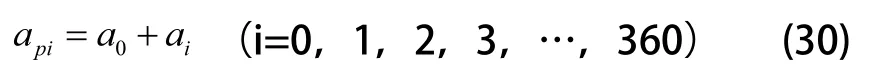
式中α0为普通外圆磨床状态下磨削深度；αi为对应任意偏心轴旋转角度因随动磨削加工产生的加工深度。

消除随动磨削产生的附加磨削深度,应沿磨削点法向叠加一个修正位移量axi，即应满足axi=-ai（i=0，1，2，3，…，360），当然要想定量的确定axi的变化值还要依靠实验结果。对式(25)进行修正，将axi想水平轴X投影得：

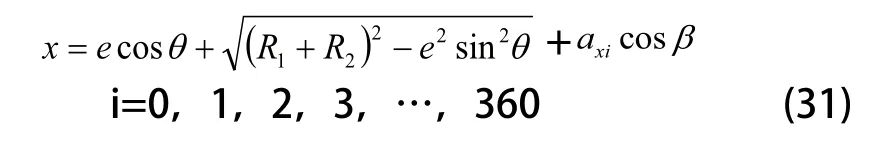
5 结论

本文首先通过建立数学模型分析了随动磨削机床加工偏心轴的加工特性并运用MATLAB仿真，直观的再现了磨削点的运动轨迹。其次根据随动磨削运动特性推导出磨削设计约束方程并得出了当偏心轴转速恒定条件下，砂轮磨削速度是变化的，当砂轮半径在一定范围内，取值越大时，砂轮围绕摆轴转动的速度变化越小。另外分析了偏心轴在恒线速度加工条件下砂轮中心位移变化值，为了保证砂轮磨削点与摆轴颈的任意加工点相切，对参数、x并进行离散化，最后对运动方程进行了有效修正。其结果对以后投入实践生产，开发出特定的偏心轴磨床误差补偿技方法，提高加工偏心轴的生产质量和效率提供了必要的条件。

[1] 王庆明.先进制造技术导论[M].华东化工学院出版社,2007.

[2] 范晋伟,宁堃.提高曲轴磨削精度的几何误差补偿技术[M].机械设计与制造,2012.

[3] D.French, S.H.Humphries. Compensation for backlash and alignment errors in a numerically controlled machine-tool by a digital computer program[J].M.T.D.R.Conf. Proc,1967.

[4] Donmez A.,Lee K.Liu C.R.,and Barash M.M.A general methodology for machine tool accuracy enhancement by error compensation[J].Precis.Eng.1986,8(4):187-196.

[5] Elshennaway A.K.,Ham I. Performance improvement in coordinate measuring machine by error compensation[J].Journal of Manufacturing Systems,1990,9(2):151-158.

[6] Lin P D, Ehmann K F. Direct Volumetric Error Evaluation of Multi-Axis Mchines[J].Int.J.of Mach. Tools Manufacture.1993,33(5):675-693.

[7] 邬义杰,项占琴.多面形非圆曲面数控磨削加工实时插补方法研[J].中国机械工程,2004,15(8):728-730.

[8] 谢胜泉,段正澄.自适应跟踪算法在非圆柱表面磨削加工中的应用[J].中国机械工程,1998,9(7):7-9.

[9] 赵广兴.H405-BF数控专用磨床[J].设备管理与维修.2006,(10):42.

[10] 资讯看板.数控机床市场[J].2011,(5):14.

Study on mathematical model of follow-up grinding of eccentric shaft

FAN Jin-wei, ZHANG Lan-qing, WU Chang-jun, LIU Kai-kai

TH114；TG659

：A

1009-0134(2017)07-0106-05

2017-03-23

北京市教委基金项目（51275014）

范晋伟（1965 -），男，河南西平人，教授，博士，研究方向为数控磨床可靠性与超精密加工。